天空双基地预警雷达长时间相参积累算法研究

王万田， 袁俊泉， 王力宝， 陈阿磊

(空军预警学院， 湖北武汉 430019)

0 引言

天空双基地预警雷达卫星轨道高度较高，信号传播距离远，目标回波信噪比较低，为了提高对微弱目标的检测能力，长时间相参积累是一种有效的处理手段。但是，由于天基发射端、空基接收端与目标之间的相对运动速度较高，长时间相参积累常常导致目标回波越距离单元走动，直接进行相参积累，回波信噪比提高不明显，探测性能严重下降。

Keystone变换是常用的距离单元走动校正的方法[1-4]，优点在于该算法不需要知道目标的速度信息，并且可以应用于多个目标的检测问题。文献[5-8]在分析回波越距离单元走动产生原因的基础上，采用sinc内插法实现距离单元走动校正。文献[9-10]采用Chirp-Z变换算法进行距离单元走动校正，并且给出了在多普勒模糊情况下的Keystone变换实现公式，验证了算法的有效性。文献[11-12]将Keystone变换用于天基雷达，通过仿真实验验证了算法的可行性，实现了基于天基雷达的弱目标长时间相参积累。

基于天空双基地预警雷达的长时间相参积累算法还未见有文献研究，本文针对天空双基地预警雷达目标回波越距离单元走动问题，将Keystone变换用于天空双基地预警雷达进行距离单元走动校正，首先在建立天空双基地预警雷达空间几何模型的基础上，分析距离单元走动特性；其次提出了基于Keystone变换的天空双基地预警雷达长时间相参积累算法流程，采用基于单元选大准则的数据处理方法，实现对多个不同距离和、不同多普勒模糊数的多目标检测；最后通过仿真验证了该算法的有效性。

1 空间几何模型及距离单元走动特性分析

1.1 空间几何模型

天空双基地预警雷达空间几何模型如图1所示，假设地球是一个圆球体，半径Re=6 378.1 km，卫星运行轨道为圆。以地球球心o为坐标中心，以赤道平面为xoy平面，初始x轴由地心指向轨道升交点，z轴以北极点N为参考，建立转动地心坐标系xyz。其中，T为卫星发射端，B为星下点，(α1,β1)为星下点B的地理纬度与经度，E为卫星升交点的地面投影，ht为卫星轨道高度，η为卫星轨道倾角，φ为卫星轨道幅角，vt为卫星飞行线速度，φtm为卫星发射波束相对于卫星速度矢量的方位角，θtm为卫星发射波束下视角，Rtm为发射距离。R为空基接收端，R′为空基接收端的地面投影，(α3,β3)为空基接收端地面投影R′的地理纬度与经度，hr为空基接收端飞行高度，vr为空基接收端飞行速度，φrm为空基接收波束相对于空基接收端飞行方向的方位角，θrm为空基接收波束下视角，Rrm为接收距离。M为被探测目标，hm为目标飞行高度，(α2,β2)为目标地面投影M′的地理纬度与经度，vm为目标飞行速度。

为了方便分析，假设空基接收端R沿正北方向飞行，目标M沿正东方向飞行，则tm时刻空基接收端R和目标M的位置矢量Rr(tm)，Rm(tm)分别为

Rr(tm)=(Re+hr)[cosαr(tm)cosβ3,cosαr(tm)sinβ3,

sinαr(tm)]T

(1)

Rm(tm)=(Re+hm)[cosα2cosβm(tm),

cosα2sinβm(tm),sinα2]T

(2)

式中，αr(tm)为空基接收端在tm时刻的地理纬度，βm(tm)为目标在tm时刻的地理经度，且满足

(3)

(4)

卫星发射端T的位置矢量Rt(tm)为

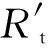
(5)

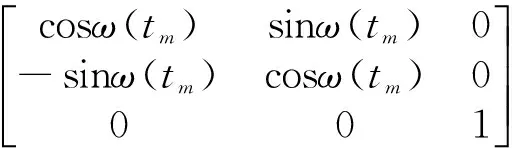
(6)

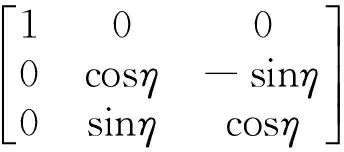
(7)

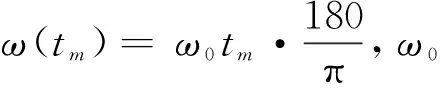
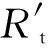
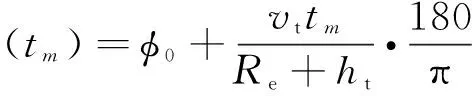
卫星T、空基接收端R、目标M三者的运动以及地球自转导致信号传播距离和发生变化，由几何关系得，tm时刻信号传播距离和Rs(tm)为

(9)

v′=ρc[vtcos(φtm+ψc)-vmcos(η+φtm+ψc)]sinθtm+

(vrcosφrm-vmsinφrm)sinθrm

(10)

式中，Rtm0为初始发射距离，Rrm0为初始接收距离，ρc,ψc为考虑地球自转时的偏航幅度与偏航角[14]，表达式为

(11)

(12)

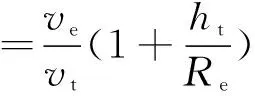
(13)

式中，ve为赤道上地球的自转线速度，且ve=0.465 1 km/s。

1.2 距离走动特性分析

假设天空双基地预警雷达发射线性调频信号，其数学表达式为

(14)

式中，f0为信号载频，τ为脉冲宽度，μ=B/τ为调频斜率，B为信号带宽。

在一个波束驻留时间内雷达发射M个线性调频子脉冲，其中第m个子脉冲可以表示为

sm(t)=s(t-tm)=

(15)

式中，tm=mTr为慢时间，Tr为脉冲重复周期。

脉冲串由天基发射端发出，经目标反射后，被空基接收端所接收。由于不同的脉冲发射时，天基发射端、空基接收端与目标之间的空间几何关系不同，距离和Rs(tm)不同，所以回波延时不同。第m个脉冲经天线接收和下变频后，可以表示为[15]

w(t′,tm)

(16)

式中，t′=t-tm为快时间，w(t′,tm)为高斯白噪声信号。

对上式沿快时间维进行傅里叶变换得

W(f,tm)

(17)

脉冲压缩频域响应函数为

(18)

式(17)与式(18)直接相乘即对回波脉冲进行脉冲压缩得

W(f,tm)H(f)

(19)

对式(19)进行傅里叶逆变换即转换到距离时域得

g(t′,tm)

(20)

式中，g(t′,tm)=w(t′,tm)*h(t′)，h(t′)为匹配滤波的时域响应函数。

由此可得，tm时刻目标回波的多普勒频率fd(tm)为

(21)

2 基于Keystone变换的天空双基地预警雷达长时间相参积累算法

2.1 Keystone变换算法原理

Keystone变换是一种常用的距离走动校正补偿算法，可以在保持回波相位的同时，校正目标的越距离单元走动，为匹配滤波后的多普勒处理奠定基础，其基本思想就是作如下变量代换[16]：

(f+f0)tm=f0τn

(22)

将式(22)代入式(19)整理得

(23)

对式(23)沿距离维作IFFT，得到距离时域-方位时域信号s′(t′,τn)为

g(t′,τn)

(24)

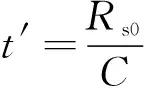
本文采用sinc内插算法实现Keystone变换，由于实际数字信号处理中，数据都是以离散形式存储的，所以首先需要把频率f、慢时间tm、虚拟时间τn离散化，S′(f,tm)对应的离散变量为S′(l,m)，S′(f,τn)对应的离散变量为S′(l,n)，算法实现公式如下：

(25)

天空双基地预警雷达体制中，相对运动速度较高，常常出现多普勒模糊问题。此时，仍可用Keystone变换进行距离单元走动补偿，需要根据多普勒模糊的程度对式(25)进行校正，具体公式[15]如下：

(26)

式中，k为多普勒模糊数，表征多普勒模糊的程度，定义为

fd=kfr+fl,fl∈[0,fr]

(27)

式中，fd为目标多普勒频率，fl为模糊的多普勒频率，fr为脉冲重复频率。

2.2 基于Keystone变换的多目标长时间相参积累算法

采用Keystone变换进行越距离单元走动补偿，在目标多普勒模糊的情况下，由于目标速度信息未知，故对应的多普勒模糊数k未知，因此需要对所有可能的多普勒模糊数(i=-k,-k+1,…,k-1,k)进行解多普勒模糊和相参积累处理[16]，得到2k+1帧距离-多普勒域相参积累结果。另外，天空双基地预警雷达天基发射端轨道高度较高，探测区域常常存在多个目标的场景，并且不同目标的多普勒模糊数不一定相同，这就需要对所有相参积累结果进行数据处理。

本文采用单元选大数据处理准则，即对2k+1帧距离-多普勒域数据选取最大值作为最终的距离-多普勒域相参积累结果，可以表示为

(28)

完成数据处理后，将相参积累结果与检测门限u0比较即可得到检测结果。

综上所述，基于Keystone变换的天空双基地预警雷达多目标长时间相参积累算法流程如下：

步骤1对原始回波数据沿距离维作FFT，变换到距离频域-方位时域。

步骤2对步骤1得到的数据矩阵乘以匹配滤波的频域响应函数H(f)。

步骤3采用sinc内插算法对步骤2得到的数据进行Keystone变换，对所有可能的多普勒模糊数(i=-k,-k+1,…,k-1,k)进行解多普勒模糊处理，并沿距离维作IFFT变换到距离时域，沿方位维作FFT进行相参积累处理，得到2k+1帧距离-多普勒域数据。

步骤4根据单元选大准则，对2k+1帧距离-多普勒域相参积累结果进行数据处理。

步骤5根据单元平均恒虚警计算检测门限u0，将相参积累结果与检测门限u0比较，若过检测门限u0则判决为有目标，否则，判决为无目标。

3 仿真与分析

天空双基地预警雷达参数设置如表1所示。

表1 天空双基地预警雷达参数

目标仿真参数在第1节建立的坐标系的基础上进行设置，目标1飞行高度5 km，初始纬度30.022°，初始经度120.025°，速度大小v1=2 000 m/s，正东方向飞行；目标2飞行高度6 km，初始纬度30.025°，初始经度120.040°，速度大小v2=500 m/s，正北方向飞行。仿真中噪声为零均值加性复高斯白噪声，虚警概率为10-6，蒙特卡洛仿真次数为200次。

3.1 距离单元走动校正效果仿真

图2给出了经目标1、目标2反射后512个脉冲距离维脉压图。从图中可以看出，无论是目标1还是目标2，其不同脉冲的回波脉压峰值出现在不同的距离和上，即发生了越距离单元走动；图3为512个脉冲经Keystone变换后的回波图，与图2相比，图3中不同脉冲的回波峰值位于同一距离单元中，即越距离单元走动问题得到解决。

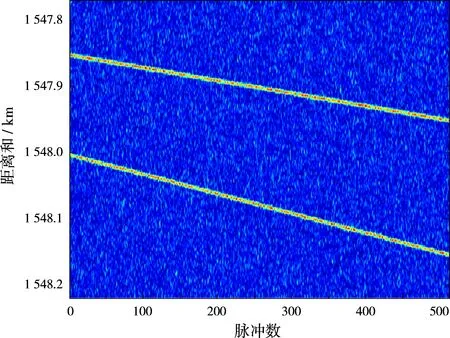
图2 距离维脉压后回波图

图3 Keystone变换后回波图

3.2 检测性能对比仿真分析

针对天空双基地预警雷达探测多目标情况，本文首先对目标1和目标2回波脉冲进行仿真并完成距离维脉压处理，其次采用sinc内插算法实现Keystone变换校正距离单元走动问题，并针对不同的多普勒模糊数i=-k, -k+1,…,k-1,k完成解多普勒模糊和相参积累处理，得到2k+1帧距离-多普勒域数据，最后根据单元选大准则对2k+1帧距离-多普勒域数据进行数据处理。

3.2.1 不同信噪比下512个脉冲的检测效果对比

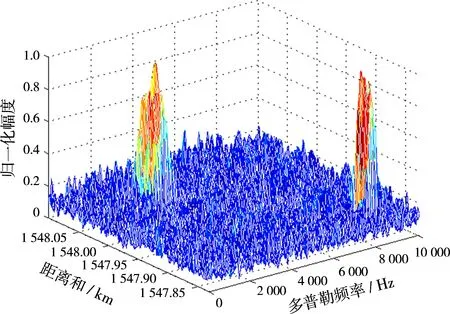
图4为目标回波信噪比SNR=-15 dB时应用本文方法以及未进行距离走动校正的常规方法相参处理结果，可以看出，本文方法与常规方法均可以检测到目标，但是常规方法相参处理后目标峰值由于距离走动而展宽。图5为目标回波信噪比SNR=-30 dB时的相参处理结果，图5(a)中目标峰值清晰可见，图5(b)中目标淹没在回波噪声中，无法检测到目标。

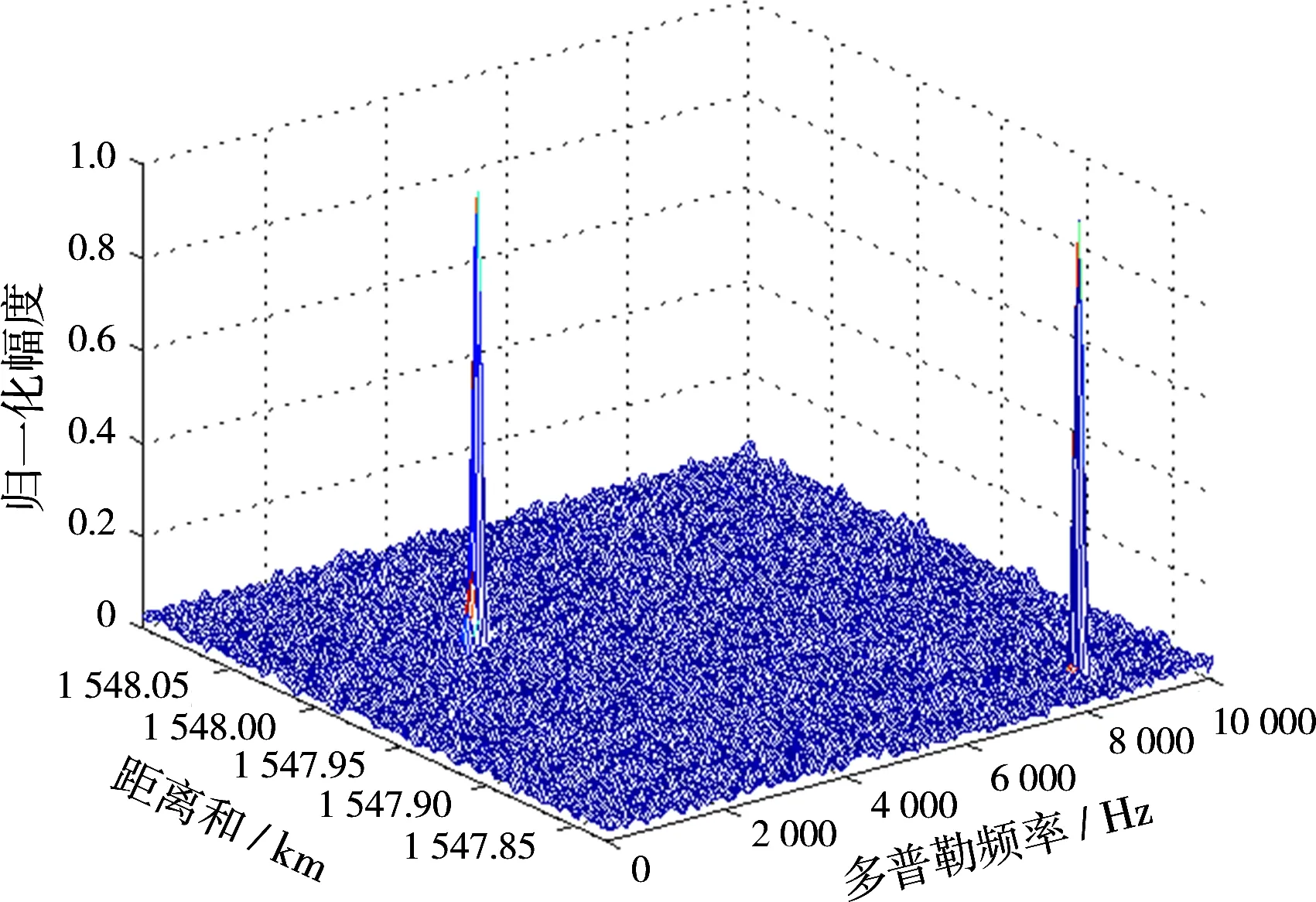
(a)本文方法相参处理结果

(b)常规方法处理结果图4SNR=-15 dB时相参处理结果

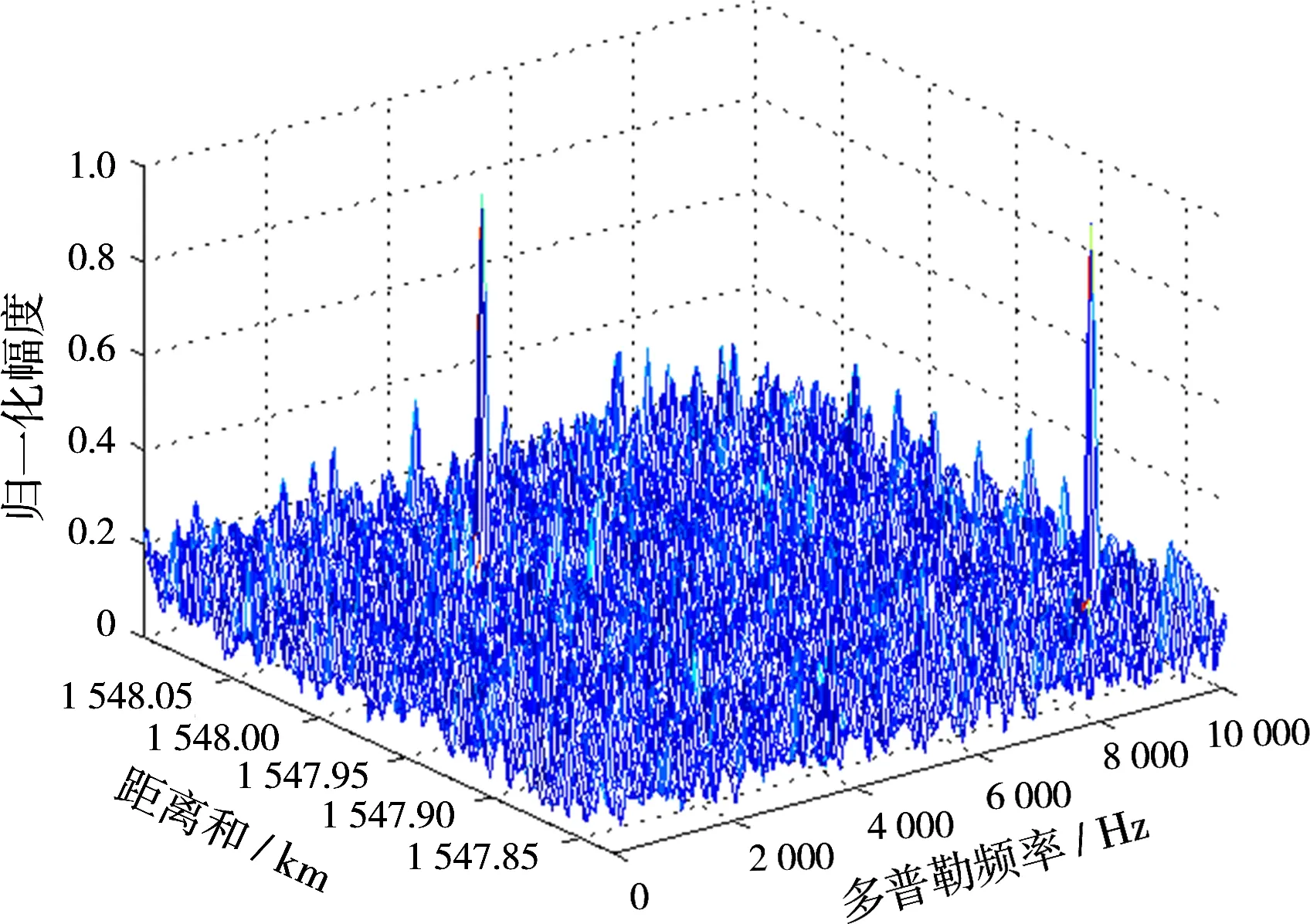
(a)本文方法相参处理结果

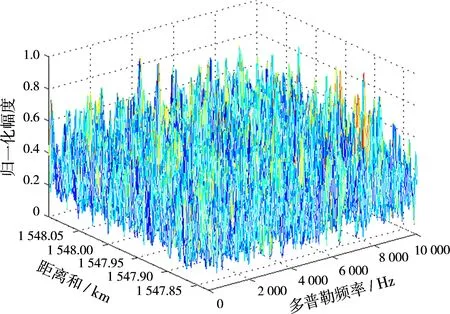
(b)常规方法处理结果图5SNR=-30 dB时相参处理结果

3.2.2 不同积累脉冲数的检测性能对比

图6、图7、图8分别给出了积累128个、256个、512个脉冲条件下采用本文方法对目标1与目标2的检测性能曲线，作为比较，同时给出了在不进行距离单元走动校正条件下的检测性能曲线。由图可知，采用本文方法得到的检测性能曲线与不利用Keystone变换校正距离单元走动情况下的检测性能曲线相比，均有不同程度信噪比增益的提高，且目标相对运动速度越高，距离走动单元数越多，采用本文方法信噪比增益提高越大。从图8可知，在不进行距离单元走动校正情况下已无法检测到目标1，由此可知，采用长时间相参积累提高目标回波信噪比时，相参积累脉冲个数越多，采用常规方法对目标的检测性能越差，必然要进行距离单元走动校正后再进行相参积累，才可有效提高目标回波信噪比。

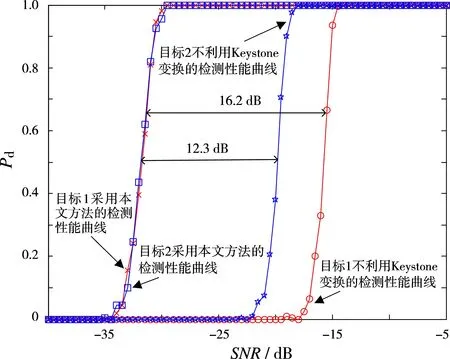
图6 积累128个脉冲时的检测性能曲线

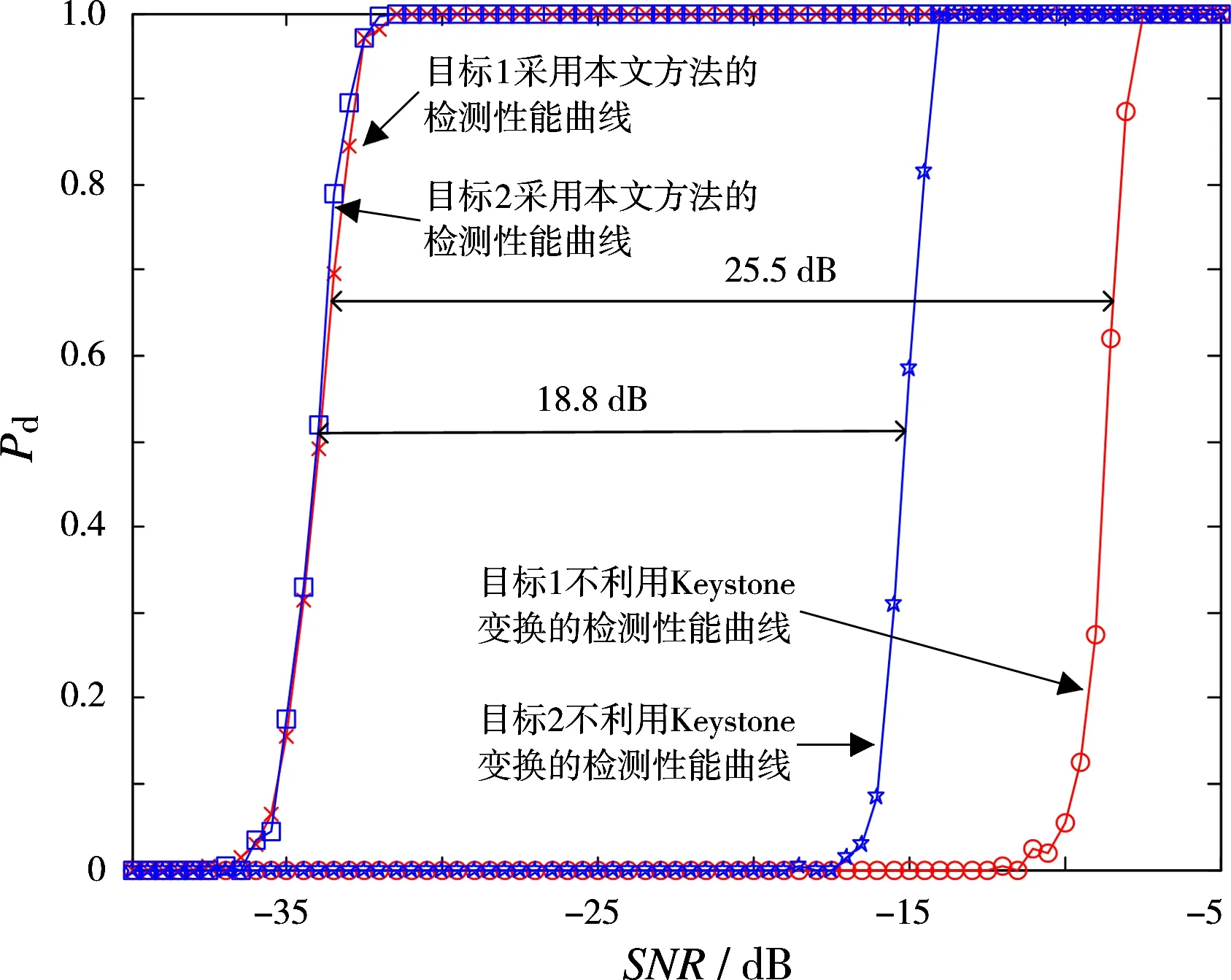
图7 积累256个脉冲时的检测性能曲线

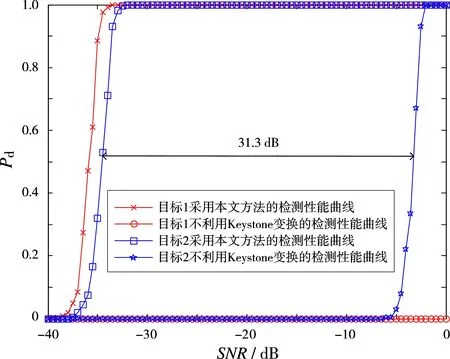
图8 积累512个脉冲时的检测性能曲线

4 结束语

天空双基地预警雷达发射端、接收端与目标之间相对运动速度较高，空间几何关系复杂，在一个相参积累时间内，难以避免回波越距离单元走动问题。本文将Keystone变换校正距离单元走动算法运用到天空双基地预警雷达体制中，在建立天空双基地预警雷达空间几何模型的基础上，研究分析了目标回波的越距离单元走动特性，提出了一种天空双基地预警雷达长时间相参积累算法，解决了目标回波越距离单元走动问题，实现了对多目标的长时间相参积累，仿真结果验证了算法的有效性。

[1]谢锡海,马小玲. 基于Keystone变换的相参积累方法[J]. 传感器与微系统, 2016, 35(9):54-57.

[2]LI Xiaolong, CUI Guolong, YI Wei, et al. Range Migration Correction for Maneuvering Target Based on Generalized Keystone Transform[J]. 2015 IEEE Radar Conference, Arlington, VA, USA:IEEE, 2015:95-99.

[3]宁娜,郝凤玉. Keystone变换实现方法研究[J]. 现代电子技术, 2011, 34(24):133-136.

[4]GUAN Xin, ZHONG Lihua, HU Donghui, et al. An Extended Processing Scheme for Coherent Integration and Parameter Estimation Based on Matched Filtering in Passive Radar[J]. Journal of Zhejiang University:Science C, 2014, 15(11):1071-1085.

[5]高玉祥,张兴敢,柏业超. 基于Keystone变换的高速运动目标检测方法研究[J]. 南京大学学报(自然科学版), 2014, 50(1):30-34.

[6]TIAN Jing, MA Lin, WANG Kun, et al. Multi-Targets Detection in DBS via Keystone Transform[J]. 2011 IEEE CIE International Conference on Radar, Chengdu:IEEE, 2011:1729-1732.

[7]李春林,吴琳拥. 基于Keystone变换的长时间相参积累研究[J]. 电子科技, 2013, 26(6):148-152.

[8]汤春林. 天基AMTI雷达信号处理若干关键技术研究[D]. 成都:电子科技大学, 2012:93-99.

[9]王娟,赵永波. 一种改进的Keystone变换算法及其在微弱信号检测中的应用[J]. 航空兵器, 2011(5):3-6.

[10]王姣. 雷达信号长时间相参积累若干问题研究[D]. 西安:西安电子科技大学, 2013:26-30.

[11]杨志伟,贺顺,吴孙勇. 天基雷达高速微弱目标的积累检测[J]. 宇航学报, 2011, 32(1):109-114. YANG Zhiwei, HE Shun, WU Sunyong. A Long-Term Accumulated Detection Approach to High Speed Weak Target from Space-Borne Radars[J]. Journal of Astronautics, 2011, 32(1):109-114.(in Chinese)

[12]汤春林,汪学刚,陈祝明. 基于距离走动校正的星载雷达空中动目标检测[J]. 电子测量与仪器学报, 2011, 25(10):829-833.

[13]郑经波,宋红军,尚秀芹,等. 地球同步轨道星载SAR多普勒特性分析[J]. 电子与信息学报, 2011, 33(4):810-815.

[14]文春艳,汪学刚,陈祝明,等. 天基雷达地面回波多普勒频率分析[J]. 电讯技术, 2009, 49(4):6-9. WEN Chunyan, WANG Xuegang, CHEN Zhuming, et al. Ground Echo Doppler Frequency Analysis of Space-Based Radars[J]. Telecommunication Engineering, 2009, 49(4):6-9.(in Chinese)

[15]郑晓东,孙晓闻,高兵,等.基于频域校正的宽带雷达相参积累研究[J].电子测量技术, 2016, 39(1):76-79.

[16]王姣,李明,陈洪猛. 基于Keystone变换的多目标距离走动校正[J]. 雷达科学与技术, 2012, 10(6):663-666. WANG Jiao, LI Ming, CHEN Hongmeng. Correction of Multi-Target Range Migration Based on Keystone Transform[J]. Radar Science and Technology, 2012, 10(6):663-666.(in Chinese)