利用灵敏电流计研究电磁动量

浦天舒，姜若诗，杨 波，宫继斌

(东华大学 理学院，上海 201620)

利用灵敏电流计研究电磁动量

浦天舒，姜若诗，杨 波，宫继斌

(东华大学 理学院，上海 201620)

从场的观点，分析灵敏电流计线圈在临界阻尼运动状态下电磁动量与机械动量的转化情况. 由于电磁动量正比于线圈偏转时的角位移，使难以测量的电磁动量成为宏观上的可观测量.

灵敏电流计；电磁动量；机械动量

电磁场是物质的一种形态，具有能量和动量,但在基础物理课程中对这一概念的解释难以深入，其原因恐怕是公式推导涉及矢量分析甚至并矢(或张量)分析的缘故. 然而，如果能将抽象的概念与熟悉的基础电磁学实验联系起来，如把场的动量跟可测的直观物理量如灵敏电流计线圈的偏转角度联系起来，就有助于从场的观点来理解电磁学的问题. 这样，通过分析灵敏电流计线圈的运动，可以看出线圈的机械动量与场的电磁动量之间是如何转化的.

1 电磁场的动量密度及电磁动量

设在具有电磁场(E,B)的空间中有自由电荷密度ρ以及自由电荷产生的电流密度J分布，则单位体积中ρ和J受到的力为

f=ρE+J×B.

(1)

对于媒质中的电磁场，应将束缚电荷及磁化电流在电磁场中所受的力也包括进来，那么电荷系统所受到的总的力密度应为

f=(ρ+ρP)E+(J+JP+JM)×B.

(2)

ρ+ρP=·D-·P=ε0·E，

J=，

因此

把它们代入式(2)，得到

f= -

(3)

(4)

这样定义的应力并矢具有对称形式. 体积分式(3)两边得到

∫Vfdv=-∫Vv.

(5)

将(5)式右边第一项化成面积分，则有

(6)

对封闭面，当S→S∞， ∮ST·ds→0，因此ε0E×B可定义为电磁动量密度[1]，即定义

gem=ε0E×B,

(7)

或定义电磁动量(亦即Abraham动量[2])为

Gem=∫V(ε0E×B)dv,

(8)

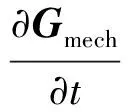
(9)

式(9)表明：在有电磁场的情况下，如果没有外力，不是机械动量守恒，而是机械动量与电磁动量之和守恒. 但若还存在外力，将引起总动量(Gmech+Gem)的改变.

2 灵敏电流计线圈运动时电磁动量与机械动量的转化

具体到灵敏电流计线圈在磁场中的运动，当线圈通有电流，如果不计电流所产生的磁场对原来磁场的影响，则线圈受到的安培力便是外力，此外线圈悬丝的扭力也是外力，而电磁动量的变化则来自线圈切割磁感线而产生的感应电场的变化. 由感应电场产生的感应电流产生的电磁阻尼力矩使线圈的机械动量减小.

根据以上受力分析，灵敏电流计线圈受到线圈电流产生的电磁力矩以及悬丝的扭力矩和感应电流产生的电磁阻尼力矩的作用，其运动方程为

(10)

(11)

式中θ为线圈偏转的角度，J为线圈的转动惯量，B为线圈所在位置由永久磁铁产生的磁感应强度，Ig为线圈平衡时通过的电流，a和b为矩形线圈的边长(线圈面积为ab)，n为线圈匝数，D为悬丝的扭转弹性系数，R为线圈回路的电阻(包括内阻及外电路电阻). 其中式(10)为给线圈瞬间通以电流(稳态值为Ig)后线圈的运动方程；式(11)为通有电流Ig的线圈突然断电后线圈的运动方程. 根据对常微分方程的解的分析可知，线圈有临界阻尼、过阻尼和欠阻尼3种运动状态，但从场的观点看，也可以从电磁动量和机械动量转化的角度来分析3种情况下线圈的运动特性.

(12)

(13)

为了能与式(12)比较，把式(13)改写成

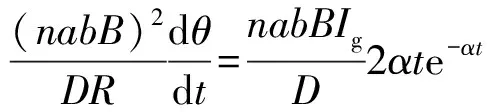
(14)

而

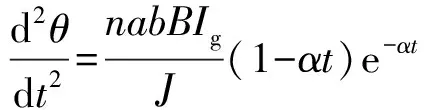
(15)

亦可改写成

(16)

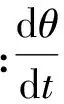
图1 临界阻尼状态下线圈的电磁动量和机械动量的时间变化率随时间的相对变化

断电瞬间，虽然Ig=0，但因线圈在磁场中偏转时产生感应电场，所以电磁动量并不为零. 通过解式(11)可知电磁动量和机械动量变化的趋势跟通电时的情况正好相反.

从以上分析可见，由于存在外力，电磁动量与机械动量不同步，而是有时间上的滞后，对于过阻尼或欠阻尼运动状态也是如此.

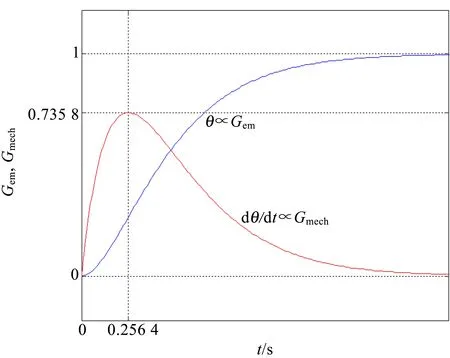
图2 临界阻尼状态下线圈的电磁动量和机械动量随时间的相对变化

3 结束语

动量表现为力在时间上的积累. 因为在给电流计瞬间通电时，3种运动状态下的机械动量最后都趋于零，所以外力的时间积累最后都表现为电磁动量，如图2所示(但在欠阻尼状态下电磁动量不是单调地增加). 另外，因电磁动量的数值非常小，一般情况下难以测量，但由于电磁动量跟线圈的偏转角度成正比，使得电磁动量成为宏观上的可观测量，而且灵敏电流计特性测量又是电磁学的基础实验，因此以上分析有助于通过机械动量与电磁动量的转换从场的观点认识灵敏电流计线圈偏转时电磁动量变化的原因：即电磁动量的变化来自于感应电场的变化，即感应电流的变化反映了电磁动量的变化，而法拉第电磁感应定律本质上反映了机械动量与电磁动量的转化与守恒定律[3].

[1] Stratton J A. Electromagnetic theory[M]. New York: McGraw-Hill， 1941:99-102.

[2] 杰克逊J D. 经典电动力学(上册)[M]. 朱培豫，译. 北京:人民教育出版社，1978:265.

[3] 张泽瑜,赵钧. 电动力学[M]. 北京:清华大学出版社,1987:108.

[责任编辑：尹冬梅]

Research on electromagnetic momentum by sensitive galvanometer

PU Tian-shu, JIANG Ruo-shi, YANG Bo, GONG Ji-bin

(College of Science, Donghua University, Shanghai 201620, China)

Transformation between electromagnetic momentum and mechanical momentum in the critical running of the coil of a sensitive galvanometer was analyzed in terms of electromagnetic field. It was shown that the electromagnetic momentum was proportional to the angular displacement of the coil so that the electromagnetic momentum, the measurement of which is generally difficult, became a macroscopically measurable quantity.

sensitive galvanometer; electromagnetic momentum; mechanical momentum

2016-05-20

浦天舒(1960-)，男，上海人，东华大学理学院副教授，学士，主要从事物理光学、微波技术的教学与科研工作.

O441.5

A

1005-4642(2017)02-0017-03

“第9届全国高等学校物理实验教学研讨会”论文