股价服从Levy过程的投资组合优化策略研究
2017-03-08张夏洁刘宣会贾丹琴
张夏洁,刘宣会,贾丹琴
(西安工程大学 理学院,西安 710048)
股价服从Levy过程的投资组合优化策略研究
张夏洁,刘宣会,贾丹琴
(西安工程大学 理学院,西安 710048)
当股票价格受到多个重大事件叠加影响时,股价会出现不连续的跳跃,一般可将股票价格考虑为服从Levy过程.基于随机微分对策,建立投资组合优化的数学模型,当股票价格服从Levy过程时,运用Ito-Levy过程的一维Ito公式和泛函变分法,采用对数效用函数,研究两人竞争的投资组合策略问题,运用随机微分对策得到两人竞争的最优投资策略.
Levy过程;随机微分对策;Ito公式;对数效用函数;最优策略
投资组合理论是数理金融学的经典理论之一,其核心思想是选择投资组合,以达到风险分散化,收益最大化和风险最小化的目的.作为一名投资者,既想要在投资的过程中获取最大的收益,同时又想承担最低的风险,需要考虑如何将资金按照一定的比例投放到不同的市场,这就出现了投资组合策略问题.即如何构建投资组合策略使得投资者可以在投资收益和投资风险中找到一个平衡点,在风险一定的条件下实现收益的最大化或在收益一定的条件下使风险尽可能地降低.
投资组合理论[1]最早是由美国著名经济学家Markowitz于1952年提出的,他开创了对投资组合进行整体管理的理论,利用均值-方差进行投资组合选择,首次将风险数量化,此后大量有关投资组合的问题开始得到深入研究[2-4].近几年,随着数学金融学和随机学等近代数学理论的发展和应用,研究最优投资组合问题已成为金融数学中的热门领域之一.其中,利用随机微分博弈理论来研究最优投资组合问题已成为热点之一[5-6].黄俏玲[7]在一个无风险资产和两个相关的风险资产组成的简单金融市场下,研究了Vasicek利率模型和Heston随机波动率模型以及投资于多个风险资产下的零和随机微分投资组合博弈问题.Browne[8]研究了股价服从几何布朗运动时两人零和随机微分对策问题.
由于在现实生活中存在很多不确定因素(如经济危机、政治事件等)会对股票价格产生冲击,使股价出现不连续的跳跃,一般将股票价格考虑为服从跳跃-扩散过程,很多学者在这方面也已经有了很好的研究成果[9-10].但是,当股价受到多个重大信息叠加冲击时,一般的跳跃-扩散模型已然无法准确的描述股价的运动.为了能更加符合实际金融市场的需求,本文在Browne研究的基础上,将股价服从的几何布朗运动过程推广到Levy过程.基于随机微分对策思想,拟建立股价服从Levy过程的投资组合优化模型,运用Ito-Levy过程的Ito一维公式和泛函变分法,根据目标函数和对策函数,采用对数效用函数,研究了两人竞争的最优投资组合策略问题.
1 模型的建立
当重大信息出现时(如经济危机,政治事件等),会对股票的价格产生冲击,出现不连续的跳跃,这时一般将股票价格考虑为跳跃-扩散模型.若受到多个冲击时,则认为股票价格服从复合泊松过程,我们将股价考虑为服从Levy过程.假设金融市场上仅有两种证券,一种是无风险资产,另一种有风险资产.
1)无风险资产(称为债券)的价格变化:dP1=rP1dt,p1(0)=p1>0,r是无风险利率.
2)风险资产(称为股票)的价格过程为:
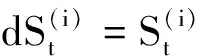
(1)
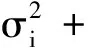
N(dt,dz)=N(dt,dz)-π(dz)dt,|z|<1
N(dt,dz),|z|≥1

引理1[12]:(复合泊松过程的Levy测度)设Xt=∑Nti=1Yi是一个复合泊松过程,N(t)的强度为λ,Yi的分布为F,则有它的Levy测度π(dx)=λdF(x).
引理2[12]:(Ito-Levy过程的Ito一维公式)假定Xt∈R是如下形式的Ito-Levy过程,其中对某个R∈[0,∞]
N(dt,dz)=N(dt,dz)-v(dz)dt,|z| N(dt,dz),|z|≥R 令f∈C2(R2),定义Y(t)=f(t,X(t)),则Y(t)也是一个Ito-Levy过程,且 dY(t)=∂f∂t(t,X(t))dt+∂f∂x(t,X(t))[α(t,w)dt+β(t,w)dB(t)]+12β2(t,w)∂2f∂x2(t,X(t)dt +∫|z| 设定投资者甲,乙均可以选择一个无风险资产(即债券)和一个有风险资产(即股票)来投资.另外规定:投资者甲仅限于在第一种股票S(1)上投资,投资者乙仅限于在第二种股票S(2)上投资. 设Xt表示甲t时刻的投资财富过程,Gt表示乙t时刻的投资财富过程. ft表示投资者甲t时刻在第一种股票上投资的财富比例,则(1-ft)表示投资者甲t时刻在债券上的投资比例. gt表示投资者乙t时刻在第二种股票上投资的财富比例,则(1-gt)表示投资者甲t时刻在债券上的投资比例. ft·[μ^1dt+σ1dWt+∫R|{0}(ez-1)N(dt,dz)]+(1-ft)rdt=[(μ^1-r)ft+r]dt+σ1ftdWt+ft∫R|{0}(ez-1)N(dt,dz) (2) (3) 定理1: (4) 由Ito-Levy过程的Ito一维公式可得: zN(ds,dz) 定义2[13]:(效用函数)非减上凸函数U∶R→(-∞,+∞)称为效用函数,若满足: 1) U′(x)存在且连续; 2)U′(x)为正的,且严格递减;3)U′(+∞)limx→+∞U′(x)=0. 常见的效用函数有U(x)=lnx(x>0)(对数函数),U(x)=xpp(x>0)(p<1且p≠0)(指数函数)等.本文选用对数函数作为效用函数进行研究. 定义4:设J(y)为泛函,y为规定的域内可以取得的曲线(简称可取曲线),y^为极值曲线,若J(y^)>J(y),则称泛函有极大值;若J() 则有:y^为极值的充要条件为:“δJ=0⟺Fy=0”. 当δ2J>0时则取得极小值,δ2J<0时取得极大值. 证明:由定理1知: 则 E[ftσ1-gtσ2)W(t)]=0 (5) (6) (7) 因而,令supf∈Ftinff∈Gtvf,g(z)=inff∈Gtsupf∈Ftvf,g(z),利用引理3求解(6)、(7)就能得到最优投资策略.根据引理3的结论有: 解得 因此 同理可得: 解得 特别地,由复合Poisson过程的特性可知:{Yk,k=1,2,…}是一族独立同分布的随机变量序列,并且与{N(t),t,t≥0}独立.若假设其密度函数为:fm(x)=λT,(0≤x≤T),则有如下结论: 根据引理1复合泊松过程的Levy测度有: λ22(ft-gt) 解得甲的最优解为: 同理解得乙的最优解为: 本文提出的模型将Browne的模型推广到更为一般的模型,考虑到当股价受到多个重大信息(如经济危机,政治事件等)叠加冲击时,股价会出现不连续的跳跃,一般的布朗运动已然无法满足实际市场股票价格变化的需求,因此研究股价服从Levy过程,对更加符合实际金融市场的需求具有重要的实际意义. 基于随机微分对策思想,在股价服从Levy过程时,运用Ito-Levy过程的一维Ito公式和泛函变分法,采用对数效用函数来研究两人竞争的投资组合优化问题.投资者甲选择投资策略期望效用最大化,同时投资者乙选择同一期望效用最小化,分别得到投资者甲乙各自的最优投资组合策略,并得到了在特定函数密度下的最优解.之后,我们将会对部分信息下股票价格服从跳跃-扩散过程的投资组合优化问题作深入的讨论和研究. [1]MARKOWITZH.Portfolioselection[J].JournalofFinance,1952, 7(1): 77-91. [2] FU C P, LI X. Dynamic mean-variance portfolio selection with borrowing constraint[J]. European Journal of Operation Research, 2010, 200(1): 312-319. [3] 王秀国, 王义东. 基于随机基准的动态均值-方差投资组合选择[J].控制与决策, 2014, 29(3): 499-505. [4] 荣 幸. 组合投资选择的随机最优控制方法[J]. 工程数学学报, 2014, 31(2): 159-165. [5] 刘海龙, 樊志平, 潘德慧. 基于微分对策的证券投资决策方法[J]. 东北大学学报:自然科学版, 1999, 20(1): 101-104. [6] 张柯妮. 基于随机LQ 控制的一类投资组合优化策略[J].纺织高校基础科学学报, 2012, 25(3): 246-250. [7] 黄俏玲, 林 祥. 零和随机微分投资组合博弈问题[D]. 长沙: 中南大学, 2013. [8] BROWNE S. Stochastic differential portfolio games [J]. Journal of Applied Probability, 1998, 37(1): 126-147. [9] 李洪宇, 王向荣. 基于跳跃-扩散过程的最优消费投资组合问题研究[D]. 青岛: 山东科技大学, 2003. [10] 赵 珺, 赵培标. 基于跳-扩散模型的最优投资策略研究[D]. 南京: 南京理工大学, 2004. [11] 张 波,商 豪. 应用随机过程[M].北京: 中国人民大学出版社, 2009. 50-51. [12] 张景肖. 随机最优控制及其在保险中的应用[M]. 北京: 科学出版社, 2013.12-114. [13] 金治明. 数学金融学基础[M]. 北京: 科学出版社, 2006. 305-322. Research on investment portfolio optimization strategy of stock prices obey Levy process ZHANG Xia-jie, LIU Xuan-hui, JIA Dan-qin (School of Science, Xi'an Polytechnic University, Xi'an 710048, China) When stock price is impacted by many major things, the stock price will not jump continuously. Generally, the price of stock is considered to obey the Levy process. Based on the stochastic differential game, the mathematical model of investment portfolio optimization was established. In the course of stock price obeying Levy, the research on the investment portfolio strategy was studied by using the Ito formula of Ito-Levy process, functional variational method and the logarithm utility function, the optimal investment strategy of the two person competition was obtained by using the stochastic differential game. Levy process; stochastic differential games; Ito formula; logarithmic utility function; optimal strategy 2015-10-12. 陕西省教育厅科研计划项目基金(2013JK0594);西安工程大学研究生创新基金(CX2015002) 张夏洁(1991-),女,硕士,研究方向:金融数学. O211 A 1672-0946(2017)01-107-06

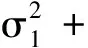


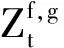

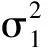




2 最优投资组合策略
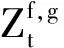


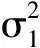
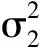

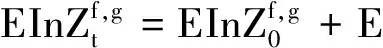
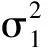


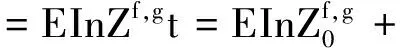

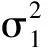
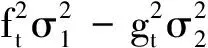


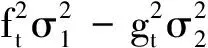

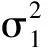

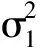
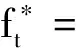

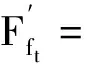


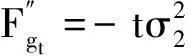
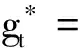
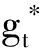




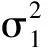
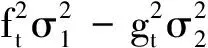

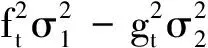
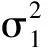

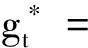
3 结 语
