伟烈亚力的中西代数学比较及其史学渊源

陈志辉

(内蒙古师范大学科学技术史研究院，呼和浩特 010022)

1 问题的提出

因第一次鸦片战争战败，中国被迫开放了上海等五个口岸城市，大量商人和传教士以这些通商口岸为据点，开展商业、宗教、科学和文化等活动。与中国人和中国历史文化的接触日渐频密，来华西人得以切切实实地了解中国本土的学术与文化，从而使得他们能够对中国文明与西方文明进行更直接而深入的比较。与此同时，科学正在欧洲快速发展并取得新颖成果，因而科学知识中西比较也成为比较史学的重要议题。传教士伟烈亚力(Alexander Wylie，1815～1887，1847年来华)，便是较早进行中西科学比较的重要学者。1852年秋，伟烈亚力在《北华捷报》上连载了英文长文《中国科学略记·算术及代数学》(JottingsontheScienceoftheChinese.Arithmetic，以下简称《略记》)*此文并无统一的中文译名。根据影响伟烈亚力甚深的《便士百科全书》“算术”条(Arithmetic)，狭义的arithmetic指算术，广义的arithmetic则包括很大一部分代数学内容[1]。从《略记》内容可知，伟氏在标题中所用的是广义的arithmetic。，介绍了中国古代数学以及当时中国数学的进展。文章随即在西方引起了较大反响，前辈学者多有论及[2- 4]。

《略记》在《北华捷报》上共分9期连载，这9部分内容按实际刊登时间大致如下：1)绪论、数学在中国的起缘、7世纪前的算书；2)7世纪到14世纪的算书；3)数码与基本算术运算，《九章算术》(上)；4)《九章算术》(下)；5)秦九韶(1208～1261)大衍术(上)；6)大衍术(下)；7)天元术、开方术；8)四元术、借根方，19世纪初古算之复兴；9)当时中国的数学研究、结语。*A. Wylie，“Jottings”，in The North China Herald，No. 108，111，112，113，116，117，119，120，121(August-November， 1852).被视为“中国代数学”的部分占据了第七和第八两次连载，体量可观。据伟氏在引言中称，他撰写此文有三个目的：1)对中国的数学成就形成更加公平的观点；2)引起人们对中国数学科学的兴趣；3)改正当时出版物中一些错误的描述[5]。*以下若无特殊说明，引用均据1897年重印本。为了达到这些目的，伟烈亚力在文章中对中西方的数学做了多方面的比较，该文也成为他中西比较科学史研究的最早实践成果之一。笔者由此产生的疑问是，伟氏是如何进行中西数学比较的，比较重点是什么？与此密切相关的是，这些深入比较的背后，他对中国和西方的数学与数学史知识的理解又从何而来，所依赖的具体文献有哪些？*前辈学者对此问题的研究也有一些成果，如汪晓勤通过比较确定了，伟烈亚力是通过杨辉《详解九章算法》、吴敬《九章算法比类大全》和程大位《算法统宗》等算书，获知《九章算术》的大致内容并作出介绍的([3]，14～16页)。解答这些问题，有助于我们进一步理解伟烈亚力的比较数学史学实践和思想。

1859年，伟烈亚力与李善兰(1810～1882)合作翻译并出版了英国代数学家棣么甘(Augustus De Morgan，1806～1871，今译为德摩根)的《代数学》(ElementsofAlgebra)。正如本文将要描述的，在《代数学》的英文和中文序言中*并非所有版本的《代数学》均附有伟烈亚力的英文序言[6]，前辈学者对这一材料也较少使用。，伟烈亚力延续了其史学方法，对中国和印度、阿拉伯和西欧的代数学进行了历史比较。在伟烈亚力看来，代数学及其历史是十分重要的，因而本文焦点集中在他关于代数学的比较史学上。汪晓勤已指出伟烈亚力所介绍的东西方数学史知识与德摩根的数学史著述，如英国实用知识传播学会的《便士百科全书》数学词条等密切相关[7]，但他尚未对《略记》和词条进行比对，因而对于这些书籍和文本如何具体地影响伟烈亚力的比较代数学史编撰的情况，尚可作进一步展开。

2 “实用知识传播学会”出版物：伟烈亚力的西方数学与数学史知识来源

2.1 英国实用知识传播学会的大众教育理念、出版物与来华新教传教士

实用知识传播学会(Society for the Diffusion of Useful Knowledge，SDUK，1826～1846)，是在约翰·罗素(Lord John Russell，1792～1878)等一批教育改革家的支持下，由英国辉格党政治家布鲁厄姆(Lord Henry Brougham，1778～1868)创立于伦敦的一个团体，旨在为广大公众——特别是贫穷低下阶层提供实用知识教育。在教育被全面普及之前的时代，该学会通过其廉价的出版物，为一般民众提供了自学的机会[8]。在伟烈亚力尚未来华的青年时代，正是该学会拥有广泛影响力的鼎盛时期。

英国实用知识传播学会(以下或简称为“英国学会”)出版了多种实用知识丛书、年历、地图、期刊和人物传记辞典等出版物，比较有影响力的有“趣味知识丛书”(The Library of Entertaining Knowledge)、《便士百科全书》(PennyCyclopaedia，以下简称《全书》)、《便士杂志》(ThePennyMagazine)等。*更详细的目录见文献[8]，242～243页。《全书》以其条目文章标题的英文首字母为序编排，正编27卷、补编2卷、续补1卷，从1833年开始一直出版至1858年。为了编辑出版《全书》，学会在世界各地设有“地方委员会”，包括在中国的广州。1833年，《全书》的广州地方委员会委员为德庇时(John Francis Davis，1795～1890)；自1837到1841年，怡和洋行商人渣甸(William Jardine，1784～1843)任《全书》广州地方委员会主席，传教士裨治文(Elijah C. Bridgman，1801～1861)、郭实腊(Karl Gützlaff，1803～1851)和马儒翰(John Robert Morrison，1814～1843)任秘书[9]。这些人当中，马儒翰是第一位入华的新教传教士马礼逊(Robert Morrison，1782～1834)之子，是英国伦敦会(London Missionary Society)成员；其他人也是与伦敦会有着密切关系的商人或传教士。在此期间，与英国学会名称完全相同的“在华实用知识传播学会”(Society for the Diffusion of Useful Knowledge in China，1834～1839)由郭实腊等人在广州创立，旨在以科学等实用知识影响当时停滞不前、保守排外的中国。*关于此学会之成立，见文献[10]。由此可见，早期来华的伦敦会传教士及其收集和传播知识的工作，与英国学会和《全书》编撰之间有着密切的联系。*除了为《全书》提供有关中国的知识外，有学者认为广州的在华实用知识传播学会还在鸦片战争期间的信息收集上发挥了重要的作用[11]。

正因为英国学会在大众当中影响很大，且与伦敦会有着密切的联系，以致到了1871年，在广州和伦敦的两个实用知识传播学会虽已结束多时，稍晚的来华传教士如艾约瑟(Joseph Edkins，1823～1905)、伟烈亚力等又再一次在中国成立了同名的学会，并仿效《便士杂志》，在中国发行《中西闻见录》([2]，59页)。另一方面，伟烈亚力本人并没有正式接受高等教育，在离开文法学校后即成为细木工学徒[12]，英国学会的出版物当是他继续学习的重要参考书之一。这一系列事实都显示出，实用知识传播学会出版物对伟烈亚力近代科学知识体系的形成有着重要的影响。

2.2 《略记》中对英国学会出版物的引用

伟烈亚力的近代科学知识来源更体现在《略记》对英国学会出版物的引用上。《略记》中就有两处明确地引用自《全书》：第一处为谈及数字的位值制时，在正文中引用《全书》“算术”条(Arithmetic)和德庇时《中国人》(TheChinese)共同持有的中国人并无位值制书写方法的论断([5]，169页)。*巧合的是，《中国人》也是学会所出版的“趣味知识宝库”丛书中的一种 [13]。第二处则是在比较四元术中的“物元”与欧洲“物术”时，以脚注形式引用《全书》“代数学”条(Algebra)([5]，186页，详见3.3小节)。

图1 《略记》中霍纳法图解([5]，185页)

《全书》中关于数学的条目是由德摩根所撰写的。德摩根于1860年寄与《保险杂志》(TheAssuranceMagazine)编辑的一通信函中明确指出，所有出现在英国学会出版物中的数学文章均出自他的手笔[14]。*感谢林力娜教授向笔者提示这则材料。前辈学者的研究也确认了德摩根为《全书》撰写数学和天文学条目超过10年([15]，205～206页)。在《略记》中还有两次明确提及德摩根：一次以脚注形式引用他的《论数学的学习与困难》(OntheStudyandDifficultiesofMathematics)([5]，183页)，此书最初也是由学会于1831年出版的[16]。另一次是在比较秦九韶开玲珑乘方法与霍纳法时，引用了德摩根的论断，即霍纳(William George Horner，1786～1837)“发现了为前人所忽视而又简单普适”的“任意高次方程解法”([5]，185页)。然而此引文并未标明出处，笔者查得是出自《全书》“乘方与开方”条(Involution and Evolution)[17]。在比较秦九韶开方术与霍纳法时，伟烈亚力展示了霍纳法的图解(图1)。该图解竖栏整齐，所求得的减根方程的每项系数后加上分号辨别，与“乘方与开方”条中第一例的图解(图2)布置极为相似，而没有使用霍纳1819年论文中[18]，各例图解都具有的标志性的连线(图3)。*随着数字位数的增多，《全书》“乘方与开方”条中各例图解并不全如第一例那样整齐，但所有图解均没有连线以显示数字之间的联系。事实上，在伟烈亚力所编撰的《数学启蒙》中，“开诸乘方又捷法”节里的霍纳法图解，除了使用中文数字外，同样是德摩根式的[19]。这也说明，不但伟烈亚力对霍纳的优先权评论来源于德摩根([7]，164～165页)，就连他对于霍纳法的理解也是从德摩根所撰写的《全书》词条而习得的，而不是直接来自于霍纳本人的论文。正是基于这样的理解，伟烈亚力才能与中算中的增乘开方术做出对比(详见3.1小节)。

图2 《全书》“乘方与开方”条霍纳法图解([17]，8页)

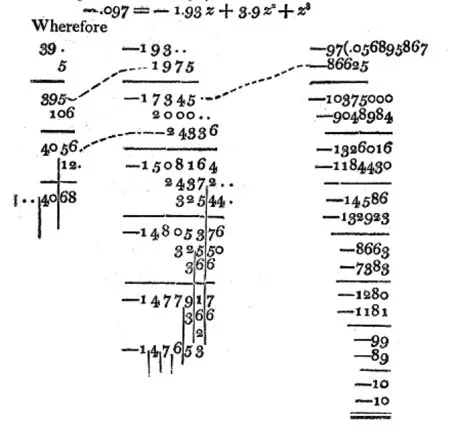
图3 霍纳1819年论文的图解[18]

《略记》还有四次以脚注形式引用西方文献，分别为卫三畏(Samuel Wells Williams，1812～1884)《中国总论》(TheMiddleKingdom)、穆雷(Hugh Murray，1779～1846)的《中国的历史与现状综述》(AnHistoricalandDescriptiveAccountofChina)、1817年11月号的《爱丁堡评论》杂志(TheEdinburghReview，orCriticalJournal)和纳皮尔(John Napier，1550～1617)的《筹算》(Rabdologi)([5]，161、167、180、193页)。从引用数量上也可以看出，《略记》对学会出版物的引用占了很大的比例。

2.3 《代数学中文序》与《全书》中的西方代数学史内容

伟烈亚力不但在《略记》中引用《全书》中的西方数学和数学史，还在他与李善兰合作翻译的《代数学》的中文序言中引用了相关的内容。该序称：

〔代数学〕创自何国何人，莫可考已。当中国六朝时，希腊有丢番都者传其法，但用数不用记号。而天竺已先有之，且精于丢氏，能推一次、二次式，并有求一法，甚赅备，几与秦九韶大衍术相埒。波斯、天方皆传其法，而精不逮焉。及元时，以大利薄那洗学自天方，以传于其国，历三百年，习者寥寥。至明嘉靖、万历间，思铁法利以其法传于日耳曼，白勒得利传于法兰西，立可传于英国，由是其学渐盛。初，天竺代未知数用五色名，波斯、天方则各用方言之“物”字。传入欧罗巴也，以大利、英国仍用“物”字，故即名“物术”云。是时，惟未知数用字代，已知数皆用本数。至肥乙大始尽以字代，是为今代数术之始。厥后学者，精益求精，创为方程式，即借根方之相等法也。[20]

引文中所提到的丢番都即丢番图(Diophantus，约3世纪)，希腊化时期亚力山大里亚数学家；薄那洗即斐波那契(Leonardo Fibonacci，1175～1250)，曾向阿拉伯人学习数学，是极具影响的中世纪意大利数学家；思铁法利即施蒂费尔(Michael Stifel，1487～1567)，白勒得利即佩尔捷(Jacques Peletier du Mans，1517～1582)，立可即雷科德(Robert Recorde，约1512～1558)，三人分别在16世纪的德国、法国和英国地区传播和发展代数学；肥乙大即法国数学家韦达(François Viète，1540～1603)，他首先运用符号代替已知量解决问题，近代代数学由此开端。

相当重要的一点是，上面所引一段代数学简史的描述源于《全书》“代数学”条。在该词条中，德摩根同样按丢番图、印度、波斯-阿拉伯到欧洲这一顺序来勾勒代数学演进的框架。因为丢番图问题(Diophantine)与印度代数的高度相似性，而后者“更为高明”，德摩根认为要么是丢番图从东方学习到了印度人的代数知识，要么是印度人在5世纪后对希腊代数学做出了很大的改进。除了提供印度与阿拉伯地区代数学的一些历史细节外，他还推荐了一些东方学家——如科尔布鲁克*科尔布鲁克(Henry Thomas Colebrooke，1765～1837)，英国梵文学家，曾翻译印度代数学经典《比贾加尼塔》(Bija Ganita或Vija-ganita)并为之撰写长篇序言。等人的相关工作。在简述13世纪以降以字(词)代数的方法在欧洲各国的发展后，德摩根提出韦达所在的时代是代数学“现代形式开始的时间”[21]。从演进的框架到定性的结论，序言中对代数学源流的“略述”，基本上是对“代数学”条相关内容的翻译和缩写。基于《全书》所介绍的西方代数学简史，伟烈亚力也得以与中国古算进行比较，并把这些比较适时地穿插在中文序对西方代数学史的描述中。*这样的比较也存在于《略记》和《代数学》英文序言当中，而且更加详细(详见3.2小节)。

3 伟烈亚力著述中对中国、印度和欧洲代数学的比较

3.1 增乘开方术与欧洲霍纳法之比较

传统中算把求数值方程正根的方法统称为开方术，要求解的数值方程称为开方式。《略记》中第一次论及开方，是在介绍《九章算术》少广章的时候，伟烈亚力意译少广为evolution，并认为少广章中的开方方法与英格兰的教科书所用方法相同([5]，172页)。更详细的讨论则是以秦九韶开方术为代表的宋元增乘开方术与霍纳法的比较。

前文提及《略记》引用了《全书》“Involution and Evolution”条的“霍纳法”——高次数值方程解法，因而《略记》把开方译为evolution是十分妥贴的，但在翻译增乘开方术这一术语的时候则出现了一些问题。在《略记》中，伟烈亚力是这样介绍秦九韶的开方术的：

这些名目(按：指实、方、廉、隅等)排列好以后，未知数通过一个叫“玲珑开方”(Harmoniously Alternating Evolution)的简单程序被求解出来，这一知识在欧洲还是相当新颖的。从秦书大量例子中拿出一个，可以很好地说明。现在要开-x4+1534464x2-526727677600的根，或求x的值。([5]，184页)

伟烈亚力提及的这个解方程的例子源于《数书九章》“望敌圆营”题：

……俱以约之，得五千二百六十七亿二千七百五十七万七千六百为定实；一百五十三亿四千四百六十四为从上廉，一为定益隅，开玲珑三乘方。[22]*汪晓勤首先揭示此方程的来源([3]，18页)。

这里描述的是一个开方式，伟氏把这段文字转化为近代代数学语言“开-x4+1534464x2-526727677600的根，或求x的值”*注意常数项的十万位数字从“5”被误写为“6”外，但所列算图不误。，并称解方程的方法为“玲珑开方”，但这不是准确的传统中算的说法。检秦九韶原书，“玲珑”一词一共只出现6处，且其中4处均以“开玲珑某乘方”的形式表述*除前揭引文外，还分别有：“以一为益隅，开玲珑翻法三乘方”(卷5)；“以一为益隅，开玲珑三乘方”(卷6)；“以北里乘上廉为实，开玲珑九乘方”(卷8)([22]，493、505、523页)。，一处为类似的“开某乘玲珑方”*“一为定益隅，开连枝三乘玲珑方，得营径”([22]，530页)。，还有一处则是对“玲珑方”或“玲珑乘方”的定义性表述：

草曰：以一为从隅；以……一十五里为从七廉；以……七十二为从五廉；以……八百六十四系负差，所乘者为益三廉；……以……得三万四千九百九十二为实，各置实、廉、隅，玲珑空耦位。([22]，524～525页)

由此可知“玲珑开方”实际上并不是一种开方的程序，“玲珑(乘)方”相当于高次方程中奇次幂系数均为零的一种特殊情况，而“开玲珑某(乘)方”则是指求这种特殊方程的根[23]。其中“玲珑”所指的是开方式中偶数位为空，犹如结构巧妙、玲珑通透的镂空之物。伟烈亚力将之译为“有规律地交错”(Harmoniously Alternating)，也是可以接受的，但是在伟烈亚力所表述的代数式中，我们已看不到“玲珑”的形象。而在《数书九章》当中，无论是求解玲珑乘方式还是其他开方式，秦九韶所采用的方法均为“增乘开方法”，即在估出根的第一位数字后，利用随乘随加的方式，求出减根方程中各项的系数，其特点正是乘法和加法运算交错运用。或许正因如此，伟烈亚力误认为“有规律地交错”所修饰的是开方或解方程的过程，而不是开方式或者方程本身。

在比较了霍纳法与所谓“玲珑开方”后，伟烈亚力提到：

尽管秦是我们发现的完整发展出解决复杂方程的第一人，但也应该注意到，他的一位同时代作者杨辉在他对《九章》的分析中，虽然没有算例，但给出了极为相似的开平方根和立方根的规则，被称为“增乘方”(Accumulating Involution)，此法引自贾宪。([5]，186页)

这里的“增乘方”当是对《详解九章算法·纂类》中“增乘〔开立〕方法”[24]沿用，并被伟烈亚力误读为“增/乘方/法”。而另一方面，因为“开方”(Evolution)的定义依赖于“乘方”(Involution)，《全书》把这两个在操作上互逆的概念置于同一词条，并在该词条中介绍了霍纳法，伟烈亚力或是受此影响而混淆了“乘方”和等价于霍纳法的增乘开方法。

然而，尽管伟烈亚力对玲珑开方式或增乘开方法字面含义的理解有偏差，却对隐藏其中的复杂的方法内涵有着准确的判断，并给出了所谓“玲珑开方”的图解(图4)。以下的推测或许可以解释这个矛盾：伟烈亚力是通过与霍纳法图解的比较进而理解增乘开方术的；但他所展示的中式开方图解明显不是来自《数书九章》，而很可能是来源于《四元释例》中的“开方释例”(图5)。

图4 伟烈亚力对“玲珑开方”的图解([5]，184页)

图5 易之瀚“开方释例”中的开方术图解([27]，19a～b页)

《四元释例》最初是易之瀚为罗士琳(1789～1853)《四元玉鉴细草》(1837)而作，主要以《四元玉鉴》中的问题为例，详细解释开方术、天元术和四元术等数学方法所要注意的规则。易之瀚把该书分为“开方释例”、“天元释例”、“四元释例”，附于罗士琳《四元玉鉴细草》后刊行。到了1839年，罗士琳改刊《四元玉鉴细草》，又为附于后的《四元释例》添加了“补增诸例”，流传广泛[25]。

《略记》中明确提到“罗茗香近年在扬州出版的《四元玉鉴》全书细草(minute illustrations)及三卷释例(three volumes of rules)”([5]，190页)*实际上罗士琳的《四元玉鉴细草》为三卷，《四元释例》为一卷。，显示出伟烈亚力在写作《略记》时曾看过罗士琳的《四元释例》。1882年，牛津大学博德利图书馆购入原属于伟烈亚力的中文古书[26]。笔者在这批古书中发现，1839年版《四元释例》的三个半叶的天头上有若干条铅笔笔记。笔记包含了一些代数式和演算步骤，以印度-阿拉伯数字和拉丁字母形式表示，是对该叶正文筹式和演草转写的尝试([27]，6b、7b、8a页)。笔者认为，这些笔记在伟烈亚力购入此书前就存在的可能性相当低，加上笔记的笔迹和伟氏本人签名的笔迹也有相似之处，它们应该是属于伟氏本人的。

易之瀚和伟烈亚力的开方法图解的特点，是把计算减根方程各项系数时的所有加法程序都布置在同一个纵栏里。这种形式的图解最先由李锐《开方说》中创造[28]，易之瀚在“开方释例”中加以沿用。*李俨曾指出易氏《释例》中的部分内容“系点窜李锐《开方说》”[29]。通过对比释例中的增乘开方法图解“乘方与开方”条中的霍纳法图解，伟烈亚力可以很容易地看出两者的相似之处，因而对“玲珑开方”和“增乘方”等术语的理解偏差并不影响他对增乘开方术内涵的理解。

3.2 天元术与印度和欧洲代数学之比较

天元术的实质，是根据题意立天元一(未知数)并列出两个等价的天元式(含未知数的多项式)，然后使两个天元式相减构造出一个开方式的解题方法([23]，128页)。伟烈亚力认为，13世纪印有“立天元一”(Setting up the Celestial Monad)的算书代表了“数学的一个新的分支”，并“可以合理地被称为中国代数学”；“天元一”中用的“一”(unity或monad)用以表示一个未知数；这种表示法“与位值理论的延伸运用相结合”，可以表示未知数的连续次幂([5]，181～182页)。

在这里，伟烈亚力把“立天元一”中的“一”译为monad或其同义词unity，并认为它相当于西方代数学中的未知数x，表明他对“立天元一”中之“一”为“借一算”的深刻理解。这一理解很可能就是来源于《四元释例》中“天元借一，其兆实肇于刘徽《九章》‘少广’所谓‘借一步之’”([27]，2a页)的判断。

对于天元式的表达方法，《略记》是这样描述的：

〔天元〕一有一个“元”字写在旁边，以区分它在算式(column)中的位置。紧接在“元”下面的是自然数的位置，以汉字“太”标示，意指这是“太极”或无穷极限之位。紧接在“元”上面的是平方项；再接着上面是立方项；再上面是四次方项，如此向上类推。……在实际操作中，用“太”字就省略“元”字；或者用“元”字就省略“太”字。值得注意的是，欧洲最受尊敬的权威郑重其事地断言，中国人不懂位值制的重要意义，我们发现在此正正相反，他们把这一原理加以推演，到达西方未曾达到的精益求精的程度。([5]，182～183页)

这里也有两点能显示出伟氏对天元术的理解与《四元释例》之间的关联。第一，伟烈亚力把天元术与位值理论相联系。他并没有详细说明他何以有这样的判断，而《四元释例》“天元释例”中的第二则，正是十进定位法则([27]，58b页)。另一方面，在宋代数学的学习上，李善兰曾为伟烈亚力提供过帮助[30]。李善兰在《四元解》中，也针对《四元玉鉴》首四问撰写了数条“算例”。他首先指出“凡算式皆自左而右，步而左为十、百、千、万，步而右为分、厘、毫、丝……”；在算例的第三条则明晰各元次幂所代表的位置——即他所说的“算格”及其排列[31]。因而认识位值在李善兰看来十分重要，以致他后来更认为中国的四元术/天元术与西方代数学的区别只是“四元别以位次，代数以别以记号，法虽殊，理无异也”[32]。伟烈亚力受其影响，在此特别提出“位值理论”，我们也就不难理解了。

第二，伟烈亚力对天元式表达和运算的描述与《四元释例》相类似。在上述引文后，伟烈亚力解释道，如果将一个天元式“乘以〔天元〕一，则算式中的每一项(term)上移一层；如果乘以〔天元〕一的平方，则上移两层；如果是立方，则三层，如此类推”([5]，182～183页)。这一描述有“天元释例”的影子：

凡逐层布算之法，以虚数为天元，旁记元字；真数为太极，旁记太字。元上必太，太下必元。故有元字不记太字，有太字不记元字。元下一层则元自乘数，又下一层则元再乘数。每下一层则增一乘。

……

凡乘法，亦齐其左右两行，对列互乘。以左行下方一层起自下而上徧乘右行，为乘第一次。又于左行转上一层亦徧乘右行，为乘第二次，所得较第一次所得递进一层。……([27]，60a页)

显然，伟烈亚力运用了“层”(stage)这一术语，这与罗士琳、易之瀚，以及李善兰《四元解》算例中的用法都是一致的。*如“凡除法，若仅有天元或仅有三元者则可以天元除。以除天元一层得太一层；以除太一层得太上一层”([31]，969页)。对于天元式的乘法运算本身，也恰恰是对“天元释例”中天元式与天元式相乘的一般情况的理解和翻译，伟氏认为实际的操作是天元式中的每一项上移(释例中的“递进”)若干层。对于他所举出的特殊情况，更为合理的操作似乎正如郭书春所言：“天元式的表示采取位置值制，故乘除数为天元幂的乘除法，只要上下移动‘元’字或‘太’字即可”([23]，131页)。

总的来说，伟烈亚力和李善兰二人对天元式的描述有不少一致性，这背后蕴藏着他们对相关问题已有的交流与互动，《四元释例》极可能是他们在交流过程中的重要参考书籍。

《略记》中只涉及天元术表示法与欧洲代数方程的比较，在《代数学》的英文序言中，伟烈亚力更进一步，把天元术与古代印度代数进行比较：

《比贾加尼塔》(原注：据科尔布鲁克译本第219页。)的一个注释本，是写于1463年一部印度代数学著作，﹝我选出﹞当中的一个表达式，与古代中国与现代欧洲的方法是等价的，这将使我们对其各自表达方式的特点有一些概念。

印度：

中国：

| 1

欧洲：

x4+6x3+5x2-12x+4

在印度的表示中，术语yavv等是一些词的首字母，即ya代表yvat-tvat“数量”，是未知量的符号，vv代表4次方，gh代表立方，v代表平方，而ru代表rúpa“绝对数字”(absolute number)。……整个天元式乘或除以〔天元一的〕多少次方，就上下移动“太”字多少层。[33]

正如伟烈亚力自己所引用的，他给出的例子来自于婆什迦罗第二(Bhskara II)《比贾加尼塔》科尔布鲁克译本，其实是第五章第145条中的一个算式，系数也完全相同[34]；对术语的解释则来自于科氏的注释([34]，139页)。《全书》“代数学”条已向读者提示参阅科氏译本，可以推断伟烈亚力也是根据这一提示而阅读科氏译著，进而展开对印度、中国和欧洲代数学的比较。

3.3 四元术与欧洲近代代数学之比较

四元术是从天元术发展而来的多元联立高次方程组代数学解法，包括四元术表示法和四元消法两部分内容([23]，131页)。《略记》没有涉及四元消法，但描述了伟烈亚力所理解的四元术表示法：

朱世杰约于1303年出版其《四元玉鉴》；在书中，他运用了“一”来代替未知量和已知量，比起其同时代的学者大大向前推进。四个“一”分别用天、地、人和物来表示。前三个一般用以(但并非必须)表示已知量，而最后一个“物”(伟烈亚力原注：“波斯人和阿拉伯人运用他们各自语言中表示‘物’的单词表示未知数，而出于同一目的，意大利人用cosa一词：由此代数学在意大利被称为RegoladelaCosa，在英格兰就被称为CossikeArt。”《便士百科全书》，卷一，325页。这一巧合令人称奇。)表示未知量。这里，我们再一次必须承认中国人的优先性，因为直到韦达所生活的16世纪以前的欧洲，任意的数字代表符号并未被用来表示任意数，而只是表示所求的量。……

由此，简单四元式或a+b+c+x被写成以下形式：

上式的平方，或a2+2ab+2ac+2ax+b2+2bc+2bx+c2+2cx+x2，如下：

一个小小的练习就足以使任何一个人很好地熟悉此算法中的一些术语。左边的是地元一或b，被移动到距离“太”有两层的那个1为b2；旁边一列，最上的2占据在与物元一的位置，代表地元与物元的两倍乘积，即2bx；……([5]，186～187页)

这里的两个四元式示例是正确的，源于《四元玉鉴》“四元自乘演段之图”后解说文字中的两个四元筹式，伟烈亚力只是把筹式数字转写为印度-阿拉伯数字。在清代较早的宛委别藏本和何刻本《四元玉鉴》中*关于《四元玉鉴》的版本，参见文献[25]，33～40页。，这两个四元筹式都是不正确的[35- 36]，后来罗士琳在《四元玉鉴细草》中首次做出校正，但并没有详细的解释校正的依据[37]。而在《四元释例》“四元释例”一章中，第一例恰恰就是解释前一筹式自乘后如何得出后筹式，即天、地、人、物四元自乘及两两相乘后如何定位([27]，68a～69a页)。由此，我们不难推想伟烈亚力仍是通过“四元释例”的这部分内容，然后加以翻译、介绍的。

伟烈亚力不把天、地、人、物四元解释为四个未知量，而解释为一个未知量、三个已知量，推论出中国人先于韦达用字母表示常数；同时，他又把物元而不是天元解释为主要的未知量x，并暗示其与“物术”之间的联系。这一结论并不正确。其原因在于“四元自乘演段之图”后有文字说明“立勾三股四弦五黄方二”，合并后得第一个筹式；之后所有涉及四元的7个问题则均分别以天元一、地元一、人元一代勾、股、弦，而以物元一为“开数”即题目所问之数——尽管勾、股、弦在题目中均为未知([25]，59，63～64，143～144页)。或许是伟烈亚力的先入为主的观念，属于直角三角形三边的勾、股、弦常以a、b和c代表，于是物元一便以x代表，因而出现了上述并不正确的比较和结论。这也说明伟烈亚力对于四元术还没有全面理解，而且直到1859年《代数学》出版时，他的这一理解并无太大改变：仍然认为天元一、地元一和人元一所代表的是已知量，仅物元一代表未知量，但不再提及与欧洲“物术”之间的联系([33]，ii～iv页)。

4 伟烈亚力的比较数学史观及其来源

4.1 德摩根的数学史观

由前面的论述可知，伟烈亚力对宋元代数学的理解和描述，在很大程度上受到《四元释例》的影响。相对地，他对于西方代数学史的发展脉络的理解则明显来源于德摩根。关于德摩根的数学史观，理查德兹有以下评论：

19世纪上半叶，德摩根处于其影响力的最高点之时，历史研究在英国正盛行。……德摩根生于伟大政治史家涌现的时代，他们通过援引英国的历史而合理化并赞颂英国的现在。在德摩根的数学史观中，他体现了同样的进步精神。……他甚为流行的作品富于历史的假想与阐释，这证明了他坚信：数学常常能通过其历史而被人作出最好的理解。[38]

也就是说，德摩根受到英国当时盛行的“历史的辉格解释”(the Whig interpretation of history)，即赞扬新教徒和辉格党人成功的革命、强调历史上那些导致进步的原则的史学倾向[39- 40]。德摩根和伟烈亚力都共同引用过科尔布鲁克所翻译的《比贾加尼塔》，事实上，这一译本收于科氏《婆罗摩笈多和婆什迦罗梵文文献中的代数，以及算术与测量》(Algebra，withArithmeticandMensuration，fromtheSanscritofBrahmeguptaandBhscara)当中。在这部著作的开头，科氏有一篇《论述》，关于为何要撰写代数学史这个问题，《论述》是这样说的：

科学的历史，如果它想要有政治史和宏大叙事那样荡人心魄的吸引力，它也不能完全拒斥趣味性和知识性。值得赞美的好奇心促使人们探寻知识的来源；而对这一过程的回顾，为相同或相近领域的研究的向前发展提供指示。……

在数学科学的历史上，一个问题问之有年：代数分析的发明归功于谁？是在什么人群、什么地域当中被发明出来？由谁来改进和发展？或者说，由谁的工作让它成形和成一体系？而最后，这一知识的传播从什么地区开始的呢？无疑，人们对为现代欧洲所立即接受知识来源抱有兴趣，尽管传播的渠道仍是一大问题。我们比较确定，阿拉伯人是我们这一研究的间接或直接的导师。但是阿拉伯人几乎不自诩他们发现了代数学。总的来说，在他们的科学文化极盛的短暂时期，他们不是发明者而是学者。而代数分析的最早的萌芽可以在希腊人中找到，虽然不能准确定年，但还是远远古于阿拉伯文明最早兴起的时代；而这一科学以一个更为高级的状态在印度人当中维持，早于阿拉伯人向近代欧洲传播的最早时代。[41]

显然，这样的一种数学史研究过程，是对现代数学的“寻根”之旅。科尔布鲁克通过对梵文数学典籍的翻译和研究，希腊—印度—阿拉伯—欧洲这样一个数学知识流传谱系得以清晰地描绘，这一研究成果成为德摩根理解近代代数学的思想资源之一，固定在他为《全书》所撰写的词条当中，成为近代代数学知识的一部分。可以说，科尔布鲁克影响了德摩根，又间接地影响了伟烈亚力。当科氏的这一谱系在19世纪初的英国形成之时，对这些文明历史上的数学知识之间比较研究也在同时进行。但是选择什么来比较？在辉格史学的框架下，那些与近代数学相一致的部分就自然被首先选择出来。如前所述，伟烈亚力在《略记》当中对中西代数学中相一致的部分描绘相当准确而精彩；而那些因外表相似而产生的错误比较，也与他受辉格史学影响，特别强调中西代数学知识的相似部分，有着密切关联。

4.2 伟烈亚力的比较数学史研究在知识和宗教上的实用取向

辉格史观的另一表现特征是对当下的极大重视。无论是科尔布鲁克还是德摩根，都抱有数学史应为当前数学研究服务的实用取向。因而，德摩根在实用知识传播学会出版物中的数学史知识也成为实用知识之一种。具体到深受其影响的伟烈亚力身上，后者的比较数学史编撰则兼具知识实用和宗教实用两重意义。

通过比较中西代数学，伟烈亚力认为，明清之际耶稣会传教士把欧洲的旧代数法“借根方”传入中国时，“西国于此术尚未深焉，殆不及天元、四元”，而到了19世纪中叶欧洲人“能如此精绝者”，乃是“好学之效”([20]，序2a页)。其言下之意，就是说中国人一向有研究这些学问的传统，但耶稣会士不能把更高级的科学知识带给中国人，但以他为代表的新教传教士通过翻译近代科学著作，就能引起他们的兴趣，帮助他们发展新科学。伟烈亚力在《代数学》英文序中写道：

许多本国学者对天元〔术〕的使用驾轻就熟，这足以证明他们有把握更精深的数学分支的天赋才能；同时他们近来的一些工作很清楚地显示，因为缺乏灵活的观念，他们在巨大的障碍下苦干。现在的这本译作担负着一个期望：通过让他们掌握一种简单的方法，使他们可以发展出他们的数学理念，从而把他们从困难中解放出来；由于他们被迫采用的方法有所不足，这些理念常常不是十分完美地被陈述出来。……

一本比德摩根著作要简单的书无疑已被选择〔出版〕*指伟烈亚力所编写的《数学启蒙》，即文献[19]。……；但是，本国学者们显示出意欲探究原理并演绎结果的倾向，据此，有这一特点的一部作品，可能比许多仅有形式规则的书，更切实地有助于向这门科学的最高级研究迈进；……([33]，iv页)

正是通过对历史上的数学与古代和当下的欧洲数学做出比较，伟烈亚力一方面承认了中国人的数学天赋和传统，另一方面也指出当时中国数学研究的困境，而《代数学》的翻译能够帮助中国数学研究走出这一困境。这就是他的比较数学史在知识进步上的实用意义。伟氏之所以选择翻译德摩根的作品，除了德摩根是著名数学家外，还有中国学者“意欲探究原理并演绎结果的倾向”这一重要原因。这是伟烈亚力在辉格式的解释框架下，以其比较数学史观考察从中国代数学史后，总结出来的数学研究传统。因而伟烈亚力向中国引入欧洲近代的代数学，与其对中国数学史的理解是密切相关的。

实用的知识同时可以转化为新教传教士们在华开展传教事业的有利资源。与伟烈亚力同为伦敦会传教士的艾约瑟重申了明末清初耶稣会士所传播的是过时的科学知识，认为“科学的极大增长”优胜于“中国学问中错误的科学”，使得基督教徒及其支持者“占有了一个最有利的位置”，“以更少的困难来说服中国人放弃其传统观念”来应对儒家的攻击。[42]作为伦敦会的传教士，伟烈亚力除了通过描述历史赞颂现在，他还通过描述数学史赞颂上帝。在《略记》的最后，他写道：

难道我们不希望，如果〔中国人〕能得到正确的引导，致使他们寻求科学真理的、别无二致的探寻精神，同样能教导他们，使他们有所准备，在一个更高、更重要的知识领域进行研究吗？——甚至使他们了解自身，以及他们的存在与上帝之间的关系——上帝之名他们依然保留，但其知识已经失传。([5]，194页)

而在《代数学》中文序中，伟烈亚力更明确地指出：

抑余自欧洲航海七万里来中土者，实爱中土之人，欲令明耶稣教，以救厥灵焉。夫帝子降世，舍生救民，乃教中至要之道，《圣经》言之甚详。而余顾汲汲译此书者，盖上帝赐人以智能，当用之务尽，以大显于世。故凡耶稣之徒，恒殚其心思，以考上帝精微之理。已知者，即以告人；未知者，益讲求之。斯不负赋畀之恩。若有智能而不用，或用之而不尽，即为自暴自弃，咎实大焉。此书之译，所以助人尽其智能，读此书者，见己心之灵妙，因以感上帝之恩，而思有以报之。是余之深望也夫。([20]，序2b～3a页)

韩琦首先注意到这两段文字，并从中揭示出伟烈亚力一如明清之际的耶稣会士，以强调和传播科学为手段，实现他们在中国传播福音的宗教理想([2]，67页)。耶稣会士与伟氏虽然都以科学作为传教手段，但他们对中国科学的历史和现状的关注点是不同的。利玛窦关注中国所无：批评中国人“没有逻辑规则的概念”，“没有人会愿意费劲去钻研数学或医学”[44]；又认为欧洲“格物穷理之法视诸列邦为独备”[45]，当中最基础的几何学更是中国所缺乏的，因而翻译了《几何原本》。伟烈亚力则关注中国与欧洲所共有：认为当时欧洲代数学所取得的成绩乃由上帝所赐的“智能”所致，通过书写可与欧洲比肩的中国数学史，他就证明了中国人同样是受上帝眷顾而被赐与智能的人([30]，ii页)，同样是能发展出相关“抽象科学”*关于伟烈亚力对“抽象”一词的理解和运用以及其数学史学含义，见Karine Chemla，“Abstraction as a value in the historiography of mathematics in ancient Greece and China∶A Historical approach to comparative history of mathematics”， forthcoming.的人群。由此，他可以更好地向中国士人介绍欧洲近代科学，进而让他们皈依上帝。这是其比较数学史在宗教传播上的实用意义。

5 余 论

通过以上的分析，我们现在已经可以基本明确，英国德摩根《便士百科全书》数学词条，是伟烈亚力比较数学史学的重要来源。同时，在撰写《略记》时，特别是进行代数学中西比较的过程中，伟烈亚力很可能在李善兰的帮助下，主要参考易之瀚和罗士琳的《四元释例》，形成了对中国古算的一些洞见。

《略记》的产生与伟烈亚力随后一系列数学翻译出版活动密切关联。事实上有一些代数学名词的翻译，如上文提到的“开方”(evolution)和“乘方”(involution)等，首先就是《略记》在描述中算史时在《全书》中找到对应的英译，然后在《代数学》的翻译中直接使用。*关于《代数学》中数学名词的翻译，参见文献[43]。另外，关于未知数次幂的表示方式，《代数学》并未使用拉丁字母上标印度- 阿拉伯数字的方式，如x3在译本中表示成“天三”，而后者正是李善兰《四元解》“算格”中天元位次的表达方式。

至此，我们还可以引申出另一个问题：伟烈亚力是在1847年来华前就已经学习代数、微积分等近代数学知识，还是来华以后，为了进行中西数学史的比较才学习相关知识？笔者倾向于后者。从上可知，伟烈亚力的近代数学知识首先来源于《全书》，而《全书》作为一部30卷本的洋洋巨著，他并无必要也无可能记住《全书》中所有的数学词条。更大的可能是，《全书》或其他的西方百科全书，是当时来华传教士的案头工具书，他们能根据需要迅速地从中获取相关知识。*感谢林力娜教授向笔者提示这一十分合理的猜测。当然，伟烈亚力在来华以前也曾努力自学关于中国的知识[46]([12]，1～3页)，我们也可以很合理地推测，他主要是以《全书》以及其他学会出版物作为入门的门径。

理查德·约认为，百科全书传统是中世纪后期以降的知识传统：百科全书包罗上帝的真理，当中对自然界的揭示，正是伽利略所称的除《圣经》外“上帝的第二本书”[47]。因为实用知识传播学会的影响，伟力亚烈从这“第二本书”中获得当时最新的数学知识，而同时又通过比较研究，把中国古代数学纳入到这本“书”里面。在这种知识传统的引领下，伟烈亚力与中国学者合作，产生了众多影响深远的工作。

致谢本文部分内容曾分别于2015年6月1日巴黎七大古代世界的数学科学(Mathematical Sciences in the Ancient World)项目讨论会和同年9月11日内蒙古师范大学科学史大衍论坛上报告，林力娜(Karine Chemla)、Agathe Keller和郭世荣教授等给予了有益的意见和建议。在论文构思和撰写的过程中，笔者曾与林力娜教授多次讨论，获益良多。牛津大学博德利图书馆中文部主管何大伟(David Helliwell)先生在我查阅资料的过程中提供了很大帮助。潘澍原博士帮助斟酌用词和表述。在此向诸位师友谨致谢忱。

1 De Morgan A. Arithmetic [C]//ThePennyCyclopaedia. Vol.I. London: Charles Knight, 1833. 337.

2 韩琦. 传教士伟烈亚力在华的科学活动[J]. 自然辩证法通讯, 1998, 20(2): 63～65.

3 汪晓勤. 伟烈亚力对中国数学的评介[J]. 中国科技史料, 1999, 19(2): 10～23.

4 Libbrecht U(李倍始).ChineseMathematicsintheThirteenthCentury:TheShu-shuChiu-ChangofCh’inChiu-Shao[M]. Cambridge, Mass.: MIT Press, 1973. 310～327.

5 Wylie A. Jottings on the Science of the Chinese. Arithmetic”[N].TheNorthChinaHerald, No. 108(August-November 1852). Reprinted inChineseResearches[M]. Shanghai, 1897. 159.

6 Wylie A.MemorialsofProtestantMissionariestotheChinese:GivingaListofTheirPublication,andObituary,NoticesoftheDeceased[M]. Shanghae: American Presbyterian Mission Press, 1867. 174.

7 汪晓勤. 伟烈亚力所介绍的外国数学史知识[J]. 中国科技史料, 2000, 21(2): 163～165.

8 McManners T.TheworkofLordBroughamforEnglisheducation[D]. Durham: Durham University, 1952. 118～126.

9 Knight C(ed.).PennyCyclopaediaoftheSocietyfortheDiffusionofUsefulKnowledge, vol.I～III & VII～XX[M]. London: Charles Knight, 1833～1835 & 1837～1841. Flyleaves.

10 Lazich M. The Diffusion of Useful Knowledge in China: The Canton Era Information Strategy[M]//Lackner M, Vittinghoff N(eds.).MappingMeanings:TheFieldofNewLearninginLateQingChina. Leiden& Boston: Brill, 2004. 315～317.

11 Chen Songchuan. An information war waged by merchants and missionaries at Canton: The Society for the Diffusion of Useful Knowledge in China, 1834-1839[J].ModernAsianStudies, 2012, 46(6): 1705～1735.

12 Thomas J. Biographical Sketch of Alexander Wylie[C]// Wylie, A.ChineseResearches. Shanghai, 1897. 1.

13 Davis J F.TheChinese:AGeneralDescriptionoftheEmpireofChinaandItsInhabitants[M]. Vol.II. London: Charles Knight, 1836. 283.

14 De Morgan A. Authorship of the Treatise on Probability Published by the Society for the Diffusion of Useful Knowledge[J].TheAssuranceMagazine,andJournaloftheInstituteofActuaries, 1861, 9(4): 238.

15 Rice A. August De Morgan: Historian of Science[J].HistoryofScience, 1996, 34: 201～240.

16 McCormack T J. Editor’s Notes[C]// De Morgan A.OntheStudyandDifficultiesofMathematics, Third reprint edition. Chicago；London: Open Court；Kegan Paul, Trench, Trübner, 1910. iii～iv.

17 De Morgan A. Involution and Evolution[C]//ThePennyCyclopaedia. Vol.XIII. London: Charles Knight, 1839. 7.

18 Horner W G. A New Method of Solving Numerical Equations of All Orders, by Continuous Approximation[J].PhilosophicalTransactions, 1819. 308～335.

19 伟烈亚力. 数学启蒙[M]. 刻本. 上海: 墨海书馆, 1853. 35b.

20 伟烈亚力. 代数学中文序[C] //[英]棣么甘. 代数学[M]. 伟烈亚力, 李善兰, 译. 刻本. 上海: 墨海书馆, 1859. 序1a～2a.

21 De Morgan A. Algebra[C]//ThePennyCyclopaedia. Vol.I. London: Charles Knight, 1833. 325～326.

22 秦九韶. 数书九章[M]. 卷8. 影印清“宜稼堂丛书”本//郭书春. 中国科学技术典籍通汇·数学卷. 第一分册. 郑州: 河南教育出版社, 1993. 530.

23 郭书春. 中国古代数学[M]. 北京: 商务印书馆, 1997. 116.

24 杨辉. 详解九章算法[M]. 影印清“宜稼堂丛书”本//郭书春. 中国科学技术典籍通汇·数学卷. 第一分册. 郑州: 河南教育出版社, 1993. 1023.

25 朱世杰, 原著. 李兆华, 校证. 四元玉鉴校证[M]. 北京: 科学出版社, 2007. 36～37.

26 Helliwell D.ACatalogueoftheOldChineseBooksintheBodleianLibrary[M]. Vol.2. Alexander Wylie’s Books. Oxford: The Bodleian Library, 1985. vi.

27 易之瀚, 罗士琳. 四元释例[M]. 清“观我生室汇稿”本(博德利图书馆藏). 1839.

28 李锐. 开方说[M]. 影印清“白芙堂算学丛书”本//郭书春. 中国科学技术典籍通汇·数学卷. 第五分册. 郑州: 河南教育出版社, 1993. 5～65.

29 李俨. 中算家的方程论[M]//中算史论丛//李俨钱宝琮科学史全集. 卷6(原载《科学》1930年第1期). 沈阳: 辽宁教育出版社, 1998. 255.

30 Edkins J. The Value of Mr. Wylie’sChineseResearches[C]//Wylie A.ChineseResearches. Shanghai, 1897. i.

31 李善兰. 四元解[M]. 影印“则古昔斋算学”本//郭书春. 中国科学技术典籍通汇·数学卷. 第五分册. 郑州: 河南教育出版社, 1993. 968.

32 李善兰. 代微积拾级序[A]//[美]罗密士. 代微积拾级[M]. 伟烈亚力, 李善兰, 译. 上海: 墨海书馆, 1859. 1a.

33 Wylie A. English preface of the translation of De Morgan’sAlgebra[M]//[英]棣么甘. 代数学[M]. 伟烈亚力, 李善兰, 译. 上海: 墨海书馆, 1859. ii～iii.

34 Brahmegupta and Bhscara.Algebra,withArithmeticandMensuration,fromtheSanscritofBrahmeguptaetBhscara. Colebrooke, Henry T. tran. London: Jonh Murray, 1817. 219.

35 朱世杰. 新编四元玉鉴[M]//宛委别藏. 第69册. 南京: 江苏古籍出版社, 1988. 4.

36 朱世杰. 新编四元玉鉴[M]. 清何元锡刻本. 1818～1822. 图2b.

37 罗士琳. 四元玉鉴细草[M]. 清“观我生室汇稿”本. 1839. 图2b.

38 Richards J L. De Morgan, the History of Mathematics, and the Foundations of Algebra[J].Isis, 1987, 78(1): 17.

39 Butterfield H. Preface[M]//TheWhiginterpretationofhistory. London: G. Bell and sons, reprint. 1959. v.

40 刘兵. 克丽奥眼中的科学: 科学编史学初论[M]. 上海: 上海科技教育出版社, 2009. 36～51.

41 Colebrooke H T. Dissertation[M]//Algebra,withArithmeticandMensuration,fromtheSanscritofBrahmeguptaandBhscara. London: Jonh Murray, 1817. i.

42 Edkins J. The future attitude of China towards Christianity[J].TheChineseRecorder, 1886, 17(11): 413.

43 赵栓林, 郭世荣. 《代数学》和《代数术》中的术语翻译规则[J]. 内蒙古师范大学学报(自然科学汉文版), 2007, 36(6): 687～693.

44 利玛窦, 金尼阁. 利玛窦中国札记[M]. 何高济, 王遵仲, 李申, 译. 北京: 中华书局, 1983. 31, 34.

45 利玛窦. 几何原本序[C]//郭书春. 中国科学技术典籍通汇·数学卷. 第五分册. 郑州: 河南教育出版社, 1993. 1151.

46 Cordier H. Life and Labours of Alexander Wylie[C]//Wylie A.ChineseResearches. Shanghai, 1897. 8～10.

47 Yeo R.EncyclopaedicVisions:ScientificDictionariesandEnlightenmentCulture[M]. Cambridge University Press, 2001. xiv, 2.