小子样条件下正态先验信息的融合
2017-03-08邱立军徐学文
邱立军,刘 勇,徐学文
(海军航空工程学院a.科研部;b.接改装训练大队,山东烟台264001)
小子样条件下正态先验信息的融合
邱立军a,刘 勇b,徐学文b
(海军航空工程学院a.科研部;b.接改装训练大队,山东烟台264001)
对于Bayes小子样检验方法,先验信息的有效性影响着统计推断的准确性。在对多源正态先验信息进行融合时,采用自助法将之转换为先验子分布,其中采用了改进的经验分布函数法进行再抽样。然后,基于专家水平确定其权重,再结合专家估计法确定各先验子分布的权重。最后,通过计算综合先验分布与假设的正态分布的差异部分的面积,对综合先验分布为正态分布的假设进行检验。案例分析表明此融合方法是有效的。
先验信息;自助法;先验分布;正态分布
在装备可靠性工程领域,对于指标验证问题,常常是现场作业样本量为小子样,同时又有多种先验信息,即在现场试验验证之前获得的和装备可靠性、维修性相关的信息,如前期试验信息、相似装备系统的信息、仿真试验信息等。在这种情况下,通常采用Bayes检验方法。这种分析方法需要科学合理地利用先验信息,因此,先验信息的可信度影响着统计推断的结果。对于多个先验数据源,需要对其进行融合,得到综合先验信息。对每个先验数据源,都应当尽可能进行规范化表示,即进行分布拟合,得到一个先验子分布。如果先验子分布为正态分布,则称先验信息源为正态先验信息。从已有研究文献来看,对正态先验信息进行融合的方法还较少。文献[1-2]采用加权平均的方法对先验子分布进行融合;文献[3]认为在能够获得先验信息的可信度或获得现场数据的情况下,采用加权融合法更为合适。事实上,当多个先验子分布均服从正态分布时,综合先验分布并不一定也服从正态分布[4]。即使服从正态分布,如果采用加权融合法,融合后的均值也会存在较小误差,而方差会存在较大误差。文献[5]根据综合先验分布与假定的正态分布的概率密度函数的最大差异来判断综合先验的正态性,这是一种根据局部差异来推测整体的方法。本文着眼于研究根据综合先验分布与正态分布之间的差异部分的面积来判定综合先验分布是否可视为正态分布。
1 先验子分布的确定
确定先验子分布即判断其服从何种分布,以及特征参数。对于先验信息为小子样的情况,主要采用自助法(Bootstrap Method)[6-9]与随机加权法(Random Weighting Estimation Method)[10-11]确定其分布类型及特征参数,二者都是对先验数据的再抽样。文献[12]指出,随机加权法并不能得到比自助法更优的估计结果,因此,采用自助法确定先验子分布模型。
设Y1,Y2,…,Yn为某一未知分布F的i.i.d子样,Yi~F(y),θ=θ(F)为总体分布F的未知参数,Fn是Y1,Y2,…,Yn的经验分布,是θ的估计值,估计误差为
式中,Tn是X和F的函数。
这样,R(Y,F)的均值和方差表征了θ(F)估计误差的均值与方差。利用计算机进行N次样本再抽样,可获得N个自助统计量R*(1),R*(2),…,R*(N)。从而,可由R*(i)的频率曲线得出Rn的概率分布,用Rn的概率分布模拟Tn的分布。于是,可通过Y1,Y2,…,Yn来估计R(Y,F)的分布特征,并估计θ(F)。
如何进行再抽样,是问题的关键。文献[13]研究认为,改进的经验分布函数法是再生样本的最好获取方法,因此,这里采用这种方法。具体如下:
1)产生U[0,1]上的随机数ξ,令η=(n-1)ξ,j=[η]+1。
2)令Y*=Yj+(η-j+1)(Yj+1-Yj),得到一个再生样本数据。
3)重复1)和2)n次,就得到一组再生子样,s=1,2,…,n。
4)重复3)N次。
得到θ的N个估计值后,利用W检验或Stat::Fit软件进行分布拟合,检验其正态性。
2 各先验子分布权重的确定
为对多个正态先验子分布进行融合,需要先确定先验信息的权重。确定先验信息权重的方法主要有:专家估计法[1]、相关函数法[14]及信息对比法[15-16]等,在工程实践中,专家估计法应用较为广泛,因为专家的经验往往比较贴近实际。专家的重要性是不同的,比如,项目总负责人就比项目一般成员的意见更具有权威性,本行专家比其他行业专家更有发言权等。因此,在对专家给出的先验子分布的权重进行集结时,要考虑专家权重的影响,并应基于专家水平确定其权重。即由管理部门根据专家的威望、专家所从事的专业、专家的工作经验、专家的技术职称等指标赋予每名专家一定的分值[17],然后求其归一化权重。
评分标准见表1。在具体评分时,若认为专家权重的某项指标的描述位于某两种程度之间,则得分可取相应的2个分值之间的数值。

表1 专家权重评分信息表Tab.1 Grading information of experts weighted
设有t位专家,其中第k位专家个人权重分值的计算方法为
式中,ak、bk、ck、dk分别表示专家威望、专业、经验、职称、以往评价业绩的分值,k=1,2,…,t。
设专家的权重向量为W=(w1,w2,…,wt),第k位专家的归一化权重为:
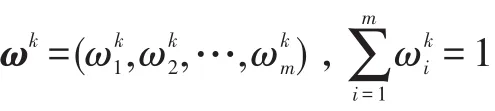
即子分布的权重向量为ω={ωi|i=1,2,…,m}。于是,可得到θ的综合先验分布πp(θ)为
3 多个先验子分布融合的综合分布模型
有的Bayes小子样检验方法,如序贯验后加权检验(Sequential Posterior Odd Test,SPOT)[18-19],要求综合先验分布能等效为一致分布,即其服从某一种分布,概率表达式中不含各先验子分布的系数。当各先验信息均服从正态分布时,综合先验分布是否也服从正态分布,取决于其均值参数的差异程度。因此,须对综合分布的正态性进行检验。
本文提出一种根据综合先验分布与假设的正态分布概率曲线图形之间的差异部分的面积(即概率)来检验综合先验分布的正态性的方法,包括准确确定特征参数。
为便于讨论,考虑n=2,Y1与Y2相互独立,的情况。步骤为:
1)取 Θ1=[a1,a2],使a1≤min(θ1-3σ1,θ2-3σ2),a2≥max(θ1+3σ1,θ2+3σ2),以ρ1≤(a2-a1)/1 000为步长,画出π1(θ)、π2(θ)以及πp(θ)=ω1π1(θ)+ω2π2(θ)的概率密度图形。
2)观察πp(θ)的形状,若它明显不是正态分布概率曲线,则认为综合先验分布不具有正态性;否则,认为,计算fp(θp)=max(πp(θ))。根据正态分布概率密度函数特性,有,于是得到σp。
3)根据Matlab函数 [CI]=max(πp(θ)),计算当fp=max(πp(θ))时的指针I,求得θp=a1+ρ1×(I-1)。

5)根据检验精度的要求,设定阈值γ∈[0 .05,0.075]。若S≤γ,则接受fp(θ)=πp(θ)的假设,即综合先验分布为正态分布;否则拒绝。
4 案例分析
在某型导弹设计定型阶段,规定采用Bayes小子样方法对其平均修复时间指标进行验证。已知导弹维修时间服从对数正态分布,须由先验信息确定维修时间均值的先验分布。
已知相似导弹装备的维修时间样本取对数后为:
导弹初样机试验阶段维修时间样本取对数后为:
用自助法分别对Y1、Y2、Y3的均值与方差进行1 000次仿真,再用Stat::Fit对均值进行分布拟合,得到各组数据的均值分布为:
接下来计算各先验子分布的权重。先求专家的权重,邀请了5位专家,其权重得分信息如表2所示。
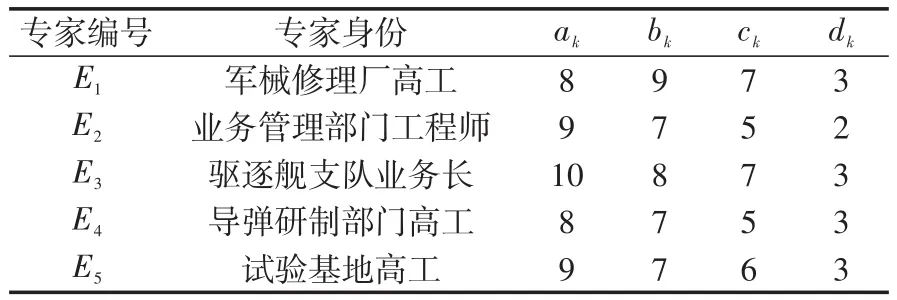
表2 专家主观权重得分信息Tab.2 Grading information of expert weight
由式(3)、(4)可得专家权重向量为:
5位专家给出的先验子分布的权重分别为(0.35,0.65),(0.37,0.63),(0.32,0.68),(0.38,0.62),(0.34,0.66)。由式(5)得ω=(0.348 6,0.651 4)。
将π1(θ)、π2(θ)与 ω 的值代入式(6),取θ∈Θ1=[3.1,4.4],以0.001为步长,生成两先验子分布与综合分布的概率密度函数曲线,如图1所示,其中虚线为融合后的综合先验分布。
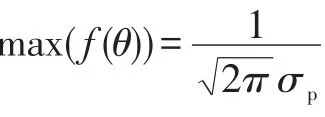
计算I=708,得θp=3.807 2。
令fp(θ)=N(3.807 0,0.155 82),取θ∈Θ2=Θ1,则综合先验与fp(θ)的图形见图2。
取γ=0.05,以0.001为步长,计算两者左半部分与右半部分曲线之间的面积,求其平均值,得出S=0.049 4<γ,因此,接受πp(θ)=N(3.807 2,0.155 62)。
5 结论
针对维修性先验信息融合后的分布问题进行了研究。首先,采用自助法将各先验信息源表征为先验子分布,在重新抽样时,采用了改进的经验分布函数法。然后,根据专家的威望、专家所从事的专业、专家的工作经验、专家的技术职称确定专家的权重,并结合专家估计法,确定各先验子分布的权重。接下来,假设各正态先验数据源融合后的综合先验分布为正态分布,通过计算综合先验分布的概率密度函数的最大值精确求出了方差;再根据密度函数为最大值时的指针计算出其均值;最后,通过计算综合先验分布与假设的正态分布图形差异部分的面积检验其正态性。
参考文献:
[1]侯敏,郭基联,李建伟.多源信息的验前分布融合方法研究[J].火力与指挥控制,2012,37(7):57-60. HOU MIN,GUO JILIAN,LI JIANWEI.Research on fusion method for prior distribution of multiple sources information[J].Fire Control&Command Control,2012,37(7):57-60.(in Chinese)
[2]冯静,周经伦,孙权.Bayes分析中多源验前信息融合的ML-II方法[J].数学的实践与认识,2006,36(6):142-145. FENG JING,ZHOU JINGLUN,SUN QUAN.Fusion of information of multiple sources based on ML-II theory in bayesian analysis[J].Mathematics in Practice and Theory,2006,36(6):142-145.(in Chinese)
[3]孙锦,李国林,许诚,等.潜射反舰导弹靶场试验先验信息融合方法仿真[J].火力与指挥控制,2014,39(8):154-158. SUN JIN,LI GUOLIN,XU CHENG,et al.Simulation research on fusion submarine launched anti method for prior distribution of ship missile in range trial[J].Fire Control&Command Control,2014,39(8):154-158.(in Chinese)
[4]姜晨,徐廷学,刘勇,等.维修性小子样验证中先验信息的融合方法[J].科学技术与工程,2014,14(22):129-133. JIANG CHEN,XU TINGXUE,LIU YONG,et al.Prior information fusion method in maintainability small sample test[J].Science Technology and Engineering,2014,14(22):129-133.(in Chinese)
[5]徐廷学,刘勇,赵建忠,等.维修性先验信息的融合方法研究[J].系统工程与电子技术,2014,36(9):1887-1893. XU TINGXUE,LIU YONG,ZHAO JIANZHONG,et al. Maintainability prior information fusion method[J].Systems Engineering and Electronics,2014,36(9):1887-1893.(in Chinese)
[6]夏新涛,叶亮,李云飞,等.基于多层自助最大熵法的可靠性评估[J].兵工学报,2016,37(7):1317-1329. XIA XINTAO,YE LIANG,LI YUNFEI,et al.Reliability evaluation based on hierarchical bootstrap maximum entropy method[J].Acta Armamentarii,2016,37(7):1317-1329.(in Chinese)
[7]JI JIAN,LI YANG.An improved SAR image denoising method based on bootstrap statistical estimation with ICA basis[J].Chinese Journal of Electronics,2016,25(4):786-792.(in Chinese)
[8]高攀东,沈雪瑾,陈晓阳,等.基于自助法的小样本Weibull分布可靠性分析[J].机械设计与研究,2015,31(2):164-167. GAO PANDONG,SHEN XUEJIN,CHEN XIAOYANG,et al.Reliability analysis under Weibull distribution in small samples based on bootstrap[J].Machine Design and Research,2015,31(2):164-167.(in Chinese)
[9]周慧,马擎宇.用自助法估计外弹道测量数据随机误差分布特性[J].飞行器测控学报,2012,31(1):75-79. ZHOU HUI,MA QINGYU.Estimation of the random error distribution characteristics of exterior ballistic measure data based on bootstrap method[J].Journal of Spacecraft TT&C Technology,2012,31(1):75-79.(in Chinese)
[10]GAO SHESHENG,GAO YI,ZHONG YONGMIN.Random weighting estimation method for dynamic navigation positioning[J].Chinese Journal of Aeronautics,2011,24(3):318-323.
[11]殷建,宋松柏.基于随机加权先验的P-Ⅲ分布参数贝叶斯估计[J].水文,2015,35(3):1-7. YIN JIAN,SONG SONGBAI.A Bayesian method for estimation parameters of P-Ⅲ distribution based on randomly weighted prior[J].Journal of China Hydrology,2015,35(3):1-7.(in Chinese)
[12]郑小兵,董景新,孟令晶,等.Bootstrap方法在导弹落点密集度评估中的误用[J].中国惯性技术学报,2012,20(2):239-243. ZHENG XIAOBING,DONG JINGXIN,MENG LINGJING,et al.Misapplication of Bootstrap method in dispersion assessment of missile fall points[J].Journal of Chinese Inertial Technology,2012,20(2):239-243.
[13]刘薇,常振海.自助法再生样本的获取方法研究[J].齐齐哈尔大学学报,2012,28(4):78-80. LIU WEI,CHANG ZHENHAI.Obtaining method research of bootstrap regenerated samples[J].Journal of Qiqihar University,2012,28(4):78-80.(in Chinese)
[14]冯静,刘琦,周经伦,等.相关函数融合法及其在可靠性分析中的应用[J].系统工程与电子技术,2003,25(6):682-684. FENG JING,LIU QI,ZHOU JINGLUN,et al.Correlation information fusion method and application in reliability analysis[J].Systems Engineering and Electronics,2003,25(6):682-684.(in Chinese)
[15]闫鹏飞,孙权.基于可信度加权融合方法在维修性评价的应用[J].计算机仿真,2010,27(6):31-35. YAN PENGFEI,SUN QUAN.Weight fusion based on credibility for maintain evaluation[J].Computer Simulation,2010,27(6):31-35.(in Chinese)
[16]王小林,郭驰名,程志君,等.一种多源先验分布权重确定的新方法[J].兵工自动化,2010,29(6):60-63. WANG XIAOLIN,GUO CHIMING,CHENG ZHIJUN,et al.A new method for determining weights of multisources of prior distribution[J].Ordnance Industry Automation,2010,29(6):60-63.(in Chinese)
[17]张荣,刘思峰.一种基于判断矩阵信息的多属性群决策方法[J].系统工程与电子技术,2009,31(2):373-375. ZHANG RONG,LIU SIFENG.Multi-attribute group decision-making method based on the information of judgment matrixes[J].Systems Engineering and Electronics,2009,31(2):373-375.(in Chinese)
[18]董博超,宋保维,梁庆卫,等.武器装备小子样维修性试验与评定方法研究[J].兵工学报,2011,32(3):327-330. DONG BOCHAO,SONG BAOWEI,LIANG QINGWEI,et al.Research on small sample maintainability experimentation and evaluation of weapon system[J].Acta Armamentarii,2011,32(3):327-330.(in Chinese)
[19]刘勇,徐廷学,彭军.维修时间截尾序贯验后加权检验的实现[J].现代防御技术,2014,42(1):106-110. LIU YONG,XU TINGXUE,PENG JUN.Realization of truncated sequential posterior odd test of maintenance time[J].Modern Defence Technology,2014,42(1):106-110.(in Chinese)
Normal Prior Information Fusion Method Under the Small Sample
QIU Lijuna,LIU Yongb,XU Xuewenb
(Naval Aeronautical and Astronautical University a.Department of Scientific Research; b.Training Brigade of Equipment Acceptance and Modification,Yaitai Shandong 264001,China)
For the small sample Bayes verification method,the effectiveness of prior information affects the correct statisti⁃cal inference.As for the fusion of multi-source normal prior information,the bootstrap method was used to convert a piece of prior information into a prior sub-distribution.Then experts’weight was determined based on their level,and the weight of the prior sub-distribution was determined by expert estimate method.At last,by calculating the discrepancy pro⁃portion between the integrated prior distribution and the hypothetical normal distribution,the hypothesis that the fused in⁃tegrated prior distribution was normal distribution was tested,and the method to accurately calculating the distribution pa⁃rameters was also put forward.The analysis by an example showed the fusion model was effective and accurate.
prior information;bootstrap method;prior distribution;normal distribution
TJ610.7
:A
1673-1522(2017)01-0111-05
10.7682/j.issn.1673-1522.2017.01.003
2016-12-01
:2016-12-14
国家自然科学基金资助项目(41476089)
邱立军(1975-),男,副教授,硕士。
