铸造气缩孔缺陷对气缸盖机械性能影响的参数化模型
2017-03-07孙林峰
孙林峰
(中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
铸造气缩孔缺陷对气缸盖机械性能影响的参数化模型
孙林峰
(中车青岛四方机车车辆股份有限公司,山东 青岛 266111)
根据试验所得的某型柴油机RuT300铸铁气缸盖的细观孔洞缺陷照片,利用编译的PYTHON程序实现了含有贴近实际形貌及随机分布孔洞的RVE参数化建模,结合FORTRAN子程序组实现RVE与宏观有限元模型间的数据传递。针对含不同细观孔洞体积分数的工字型试件,在单轴拉伸加载条件下进行了线弹性和弹塑性力学的仿真分析及试验分析,通过结果对比验证了多尺度参数化计算模型的准确性,为进一步的相关动力设计提供了量化参考。
孔洞缺陷; 多尺度; 有限元
1 引 言
作为常见的铸件,尽管经过一系列的优化工艺后,宏观铸造孔洞缺陷基本会被消除[1-4],但内燃机气缸盖在细观尺度上的微孔洞仍大量存在[5]。在恶劣的工作环境下,这些细观缺陷往往会诱发宏观失效[6-8],故对这类细观非均质材料的多尺度力学研究[9]便显得尤为重要,而目前应用最广的则是代表性体积元(RVE)法[10-11]。然而这涉及到细观变形场的手动提取及对RVE的细观加载等问题,且其细观孔洞缺陷的建模也过于理想化。本文针对这一问题,以某型柴油机气缸盖材料为例,建立了能够实现计算并行化、细观孔洞实际化的计算模型,并通过仿真软件结合汇编语言进行了有限元计算,通过与试验结果的对比,证明了该方法的可靠性与准确性,为动力装置的研究提供了一种新的设计校核思路。
2 宏细观孔洞缺陷比较
以气缸盖所用的RuT300铸铁材料为例,经过工艺优化[12]后,宏观气缩孔缺陷基本消除(如图1(a)),但经过细观检测发现,在宏观气缩孔优化区域内部含有数量不等、形貌不同的细观孔洞及裂纹,属于典型的非均质材料。通过照片可知,铸件气孔常常会呈现出近似椭球形(如图1(b)),而缩孔则是带有数个不规则枝杈的尖细状(如图1(c)),这是由于其生长力学情况不同所致。

图1 RuT300气缸盖宏细观孔洞缺陷图 (a) 铸造工艺优化前后宏观孔洞缺陷区域对比图; (b) 细观铸造气孔; (c) 细观铸造缩孔Fig.1 Multiscale void comparison for RuT300 cylinder head (a) Macro void comparison for applying casting optimization; (b) Micro gas void; (c) Micro shrinkage void
对于传统RVE法的计算,其思路为:首先根据给定的孔洞体积分数,利用Eshelby法[13]建立含有球形或椭球形孔洞的RVE单胞模型,根据对其进行弹塑性有限元分析,得到的结果进行宏观均匀化后,将其视为宏观材料的力学表现,故可被称为“单向(细观—宏观)”的数值方法。但实际上,材料内部各个部位的孔洞体积分数并不相同,且其形貌也并不规则。在本文提出的“双向”多尺度计算模型中,不仅可以生成含有更加贴近实际微孔洞形貌和分布的RVE模型,更能实现多尺度计算的自动化,只需给出宏观试件的加载条件,便可直接获取各个尺度下的力学结果,避免了计算过程中数据的手动提取,提高了计算效率。
3 RVE的有限元建模
利用PYTHON编译的程序,以任意的孔洞体积分数fp作为输入量,孔洞形貌通过对椭球的长短轴长度之比f=ha/hb进行随机取值、孔洞分布设为常见的泊松分布。当f→0时,孔洞形貌趋向于铸造缩孔类型;当f→1时,孔洞形貌趋向于铸造气孔类型。这就使得生成的RVE模型能够较好的满足上一章所示的细观孔洞照片结果,具体建模过程如图2所示,通过施加边界变形条件,使得RVE的变形最终由C1~C4四个代表性角点控制。模型建立之后,考虑到内部结构的复杂性,故而选取四面体C3D4单元对模型进行有限元网格的划分。
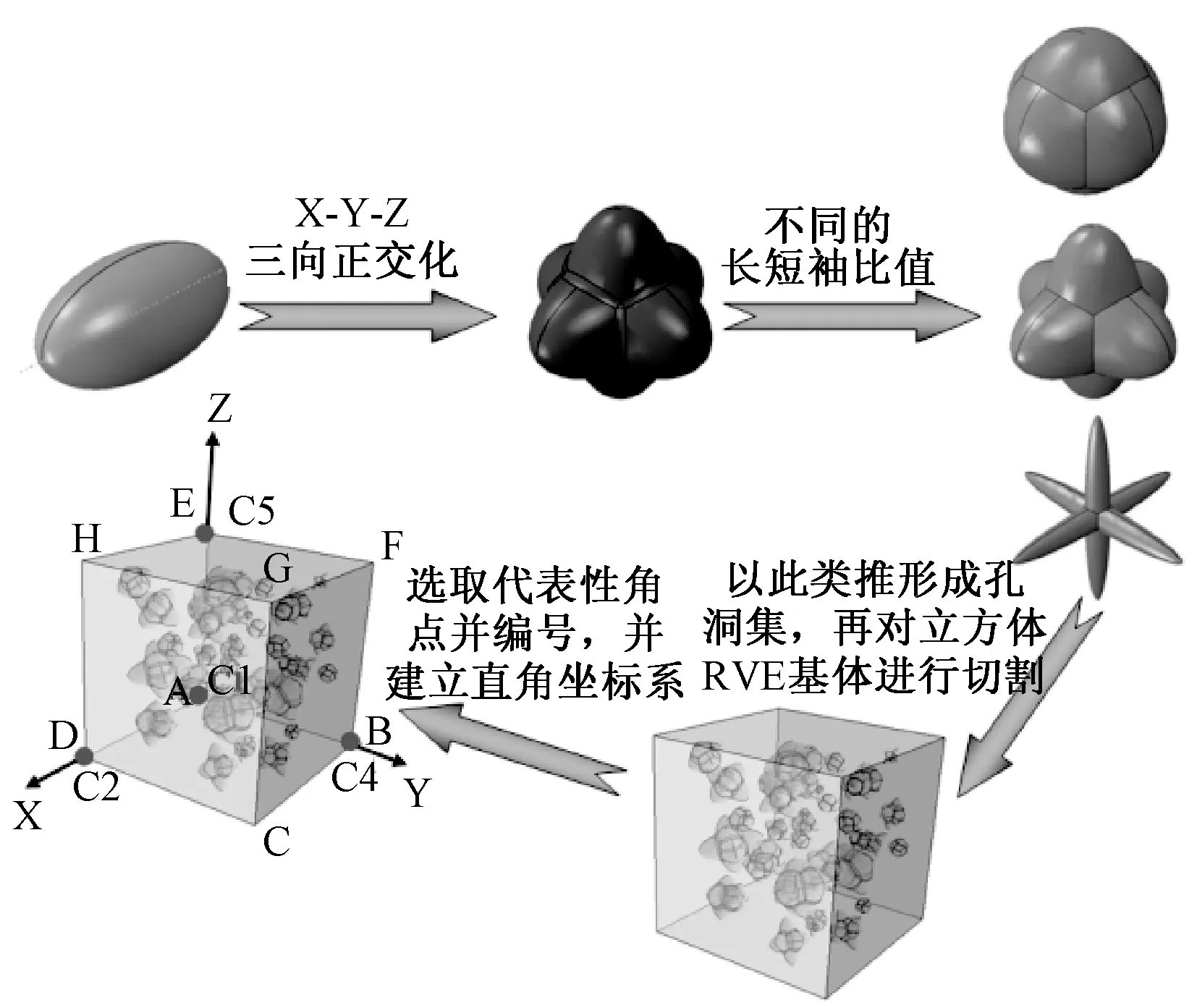
图2 含有随机孔洞的RVE模型Fig.2 RVE model containing random voids
为了确定RVE的尺寸参数,本文选择了4组(0.08mm, 0.1mm, 0.2mmand0.3mm)长度值作为RVE立方体基体的边长,通过计算在孔洞体积分数fp=0.04条件下的等效弹性模量值来进行对比分析。每组长度计算5次,每次计算时RVE的孔洞分布及形貌均各不相同,计算结果如图3所示。

图3 不同RVE边长值条件下的等效弹性模量Fig.3 Equivalent elastic modulus values under different RVE size
以最后一组(0.3mm)结果平均值正负0.1%为代表性结果边界,可以看出当RVE变长尺寸小于0.2mm时,每次计算的误差有逐渐增大的趋势,不能稳定地反映其力学性能;而相对于网格数急剧增大的0.3mm组,0.2mm组的数值与其差别并不大,但是其计算时间却更短。基于收敛性分析结果,本文选择0.2mm作为RVE立方体基体的边长值。
3 弹塑性多尺度数值仿真及试验
本文提出的并行化计算流程如图4所示。为了研究细观孔洞对宏观材料力学性能的影响程度以及验证本文建立计算模型的准确性,故选取一组经无损探伤检测后确定的含有不同孔洞体积分数fp(2%、4%、6%和8%)的工字型RuT300铸铁试件(如图5(a))进行单轴拉伸试验及仿真分析。试验设备为CTM万能试验机(如图5(b)),试件尺寸及孔洞缺陷分布区域如图5(c)和(d)所示。定义基体的杨氏模量为155000MPa,泊松比为0.27,采用Von Mises屈服准则,屈服极限为340MPa。

图4 并行化多尺度计算模型流程图Fig.4 Flowchart of the multiscale concurrent computation model

图5 单轴拉伸试验及仿真条件 (a) RuT300工字型试件; (b) CTM万能试验机; (c) 试件尺寸; (d) 加载方向及孔洞缺陷的存在位置Fig.5 Experimental and simulation conditions (a) RuT300 specimens; (b) CTM universal testing machine; (c) Size of the specimen; (d) Loading condition and void defect section

图6 两种孔洞缺陷条件下的应力对比图 (a) 无缺陷工字型试件应力云图; (b) 5%孔洞缺陷工字型试件宏细观应力云图Fig.6 Stress comparison under different defect conditions (a) No-void condition; (b) Multiscale stress contours of 5% void volume fraction condition
首先进行线弹性阶段的仿真计算,拉伸幅值取5,图6(a)和6(b)分别表示了无缺陷和孔洞体积分数fp=5%试件的线弹性仿真计算结果。
通过对比发现,在相同的加载条件下,含微孔洞的试件会提前在横贯截面处形成一条高应力带,从而成为宏观断裂的诱发条件,而此时其内部孔洞间及孔洞表面处的应力分布结果也证明了在X方向处的应力总体明显高于Y方向处的应力值,即X方向更易发生孔洞的扩展,此结果与如图7所示的探测照片相符,这就证明了本文提出的计算模型可以为宏观高应力带的形成提供很好的细观解释。
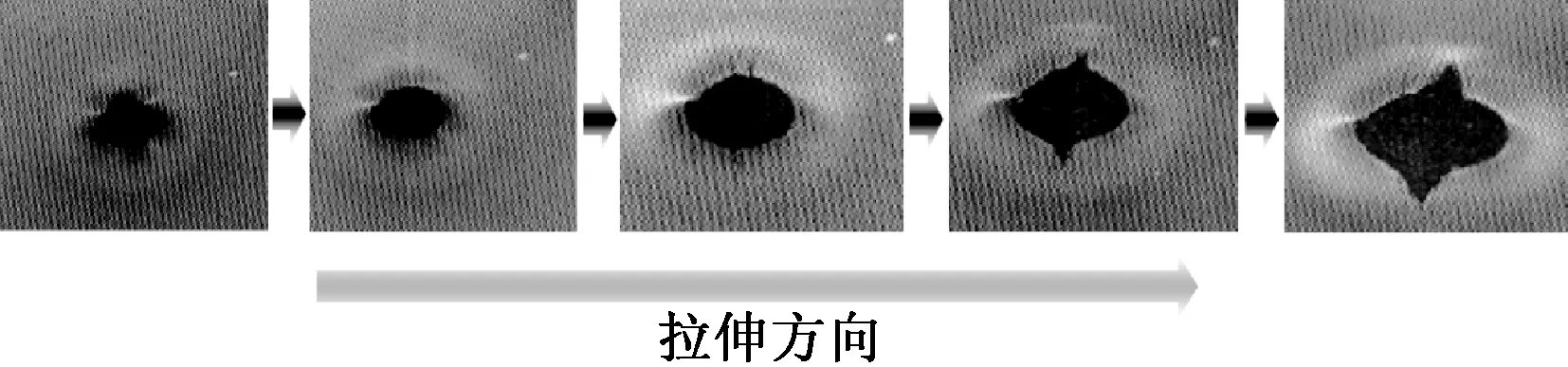
图7 微孔洞演化过程Fig.7 Propagation procedure of micro void

图8 两种孔洞缺陷条件下的应力—应变曲线Fig.8 Stress-strain curves under two defect conditions
接下来进行的是一组不同孔洞体积分数(2%、4%、6%和8%)试件模型的弹塑性多尺度仿真及实际试件的单轴拉伸试验,并选取试件颈缩前的应力和应变值。图8所展示的为fp=2%和fp=8%两种试件的仿真结果拟合曲线与试验结果的对比图。在剔除奇异的结果数据点后,通过比较发现仿真计算结果与试验值相差不大,总体趋势基本吻合。
对于细观RVE的屈服行为,其含缺陷与否的对比更加明显,图9(a)和(b)所示的分别为宏观拉伸变形率为0.5%和0.55%条件下的细观应力分布。可以看出尽管在变形率为0.5%时,宏观等效应力值为326.5925MPa,并未达到屈服极限,但是在细观孔洞之间却早已存在数条高应力带;而当变形率为0.55%时,宏观等效应力值为342.1376MPa,刚刚到达屈服极限,而细观孔洞之间的高应力带则急剧扩大,应力值的增幅也很明显,这就为产生不可恢复的塑性变形甚至断裂提供了诱发条件,从而解释了含孔洞缺陷的RuT300试件更易发生断裂的宏观现象。将若该过程发生在柴油机气缸盖中,则会造成缸盖出现局部塑性变形,从而使得缸盖漏油漏水甚至开裂造成失效。
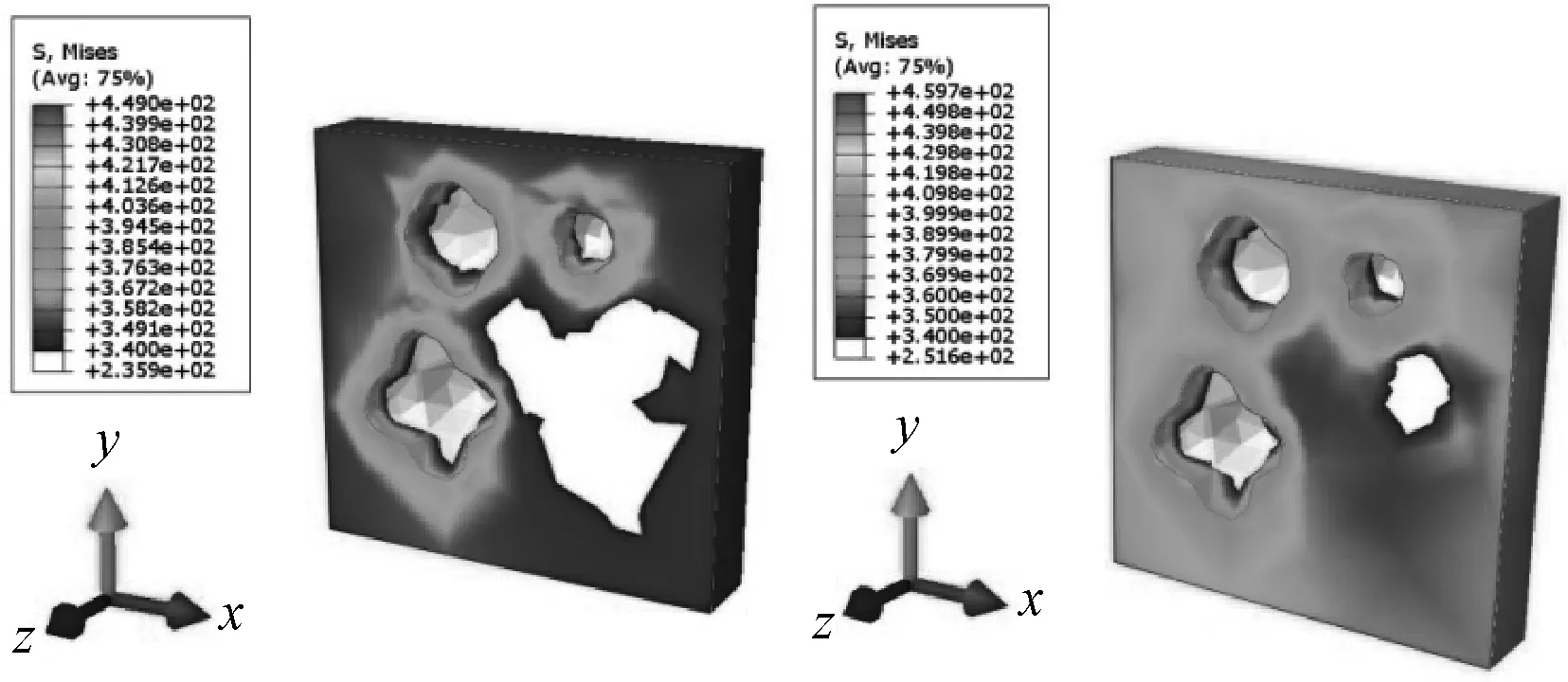
图9 宏观拉伸变形率为0.5%和0.55%下的RVE细观应力分布Fig.9 RVE stress distributions under different macro tension deformation ratios
本文以某型气缸盖所用RuT300铸铁为材料对象,针对其存在细观微孔洞缺陷这一特点,使用建立的多尺度计算模型分析了其线弹性和弹塑性的性能变化。与传统RVE法相比,本文建立的计算模型首先其得到的结果精度较高,结合不同试件的拉伸试验,试验值与仿真值总体趋势相同,相对误差较小;其次,该模型所生成的RVE其内部包含的微孔洞更加贴近实际,并且通过参数化建模,能够模拟细观孔洞体积分数分布不均匀这一现象,从而更好的进行仿真求解;最后,通过在保证计算精度的基础上能够明显提高计算效率。根据得出的仿真值,为工程上研究复杂分布状态的细观缺陷对宏观结构力学性能的影响程度提供了一种量化的手段。
[1] 蒋文明,樊自田.消失模铸造铝合金孔洞缺陷特征及形成机理[J].华中科技大学学报(自然科学版), 2012, S2:64~67.
[2] 李小龙.铸造缺陷的三维重构及其对铸件服役性能的影响[D]. 南昌大学硕士学位论文,饶磊, 南昌, 2012,5~10.
[3] 张大付.镁合金低压消失模铸造典型缺陷试验研究[D].华中科技大学硕士学位论文,樊自田, 武汉, 2005.
[4] 张杰,陈继志,冯刚宪.铸件中孔洞缺陷对疲劳性能影响的研究进展[J].材料开发与应用, 2011, 5:83~87.
[5] 万谦.铝合金压铸件微观孔洞的三维特性及其对疲劳性能的影响[D].华南理工大学硕士学位论文,广州, 2013.
[6] 闫洁,余欢.基于ANSYS软件对SiCp/Al(ZL102)复合材料铸造渗流过程多孔介质结构的有限元处理[J]. 材料科学与工程学报, 2005, 23(4):581~584.
[7] 闫英杰,曹睿,杜挽生,等. 一种新型980MPa高强钢在不同温度下的拉伸断裂试验[J].材料科学与工程学报, 2009, 27(2):246~249.
[8] 姜肃猛,齐义辉,孙广天,等.定向凝固NiAl合金的拉伸行为研究[J].材料科学与工程学报, 2005, 23(3):444~447.
[9] 裴世元,徐华.非均质复合材料力学性能的确定性多尺度计算方法[J].西安交通大学自然版学报, 2015, 10(49):8~13.
[10] T. Taxer, C. Schwarz, W. Smarsly, E. Werner. A finite element approach to study the influence of cast pores on the mechanical properties of the Ni-base alloy MAR-M247[J]. Materials Science & Engineering A, 2013, 575: 144~151.
[11] D. Bigaud, P. Hamelin. Stiffness and failure modeling of 2D and 3D textile-reinforced composites by means of imbricates-type elements approaches[J]. Computers and Structures, 2002, 80:2253~2264.
[12] 李统字,苏广才.M3000蠕铁气缸盖气缩孔的成因及解决措施 [J].热加工工艺, 2010, 3:75~77.
[13] ESHELBY, J. D. The determination of the field of an ellipsoidal inclusion and related problems[J]. Proceedings of the Royal Society A, 1957, 241:376~396.
Parameterized Model for Cylinder Head Mechanical Behavior Influenced by Casting Void Defect
SUN Linfeng
(CRRC Qingdao Sifang Co., Ltd, Qingdao 266111, China)
Based on the photographs of the microscopic void defects existing in the cylinder head which was made of RuT300 cast iron, RVE models containing with various voids which were close to reality had been generated by PYTHON coding. By using FORTRAN code, a set of subroutines were established to realize the function of data transfer between RVE and macroscopic finite element model. Uniaxial tension experiments and simulations were respectively applied on the specimens who had different micro-void fractions, and then linear elastic and elastoplastic results were obtained. Accuracy was verified by comparing the results of relevant experiments and simulations, and the claimed method in this paper could provide quantification reference for the engine design.
Void-defect; multi-scale; FEM
1673-2812(2017)01-0110-05
2015-12-22;
2016-02-25
国家留学基金委资助项目(201306030010);国家自然科学基金资助项目(104010205)
孙林峰(1986-),硕士,研究方向:材料结构强度及仿真。E-mail: sunlinfeng1986@163.com。
TK425
A
10.14136/j.cnki.issn 1673-2812.2017.01.022
