空间索面悬索桥空缆线形分析
2017-03-07张永水吴章旭
张永水,吴章旭,冯 伟
(重庆交通大学 土木工程学院,重庆 400074)
空间索面悬索桥空缆线形分析
张永水,吴章旭,冯 伟
(重庆交通大学 土木工程学院,重庆 400074)
空间索面悬索桥的鞍座曲线对空缆线形分析有较大的影响,若还是采用虚焦点法分析空缆线形将会得到不准确的结果。采用两种方法分析空缆线形的鞍座影响:解析迭代法在鞍座曲线上找切点分析空缆线形;基于ANSYS有限元软件准确模拟主缆与鞍座的接触关系分析空缆线形。两种方法的计算结果完全一致,均可作为空间索面悬索桥空缆线形的计算方法。
桥梁工程;空间索面;鞍座曲线;空缆线形;解析法;有限元
0 引 言
空间索面悬索桥主缆在塔顶之间的横向间距较小,因此主塔不必像平行索面悬索桥那样设计成H型框架结构,主塔的设计有了更大的自由度。设计时不仅能考虑结构的安全可靠而且能够与该地区的人文风俗、环境相融合,目前这一新的结构体系,主要用于人行桥和小跨径桥梁中。
主索鞍的鞍槽曲线设计成空间弧线主要是为了成桥状态主缆的走向在鞍槽出口处与曲线相切,由于空间索面悬索桥具有立面矢跨比和平面矢跨比,因此主索鞍曲线在设计上一般采用平面圆弧和立面圆弧组合而成的曲线要素。基准索股的架设若还是采用MIDAS一次成桥倒拆模型的空缆线形再修正到基准索股存在以下问题:①索股的横向受到主索鞍曲线的约束,无法考虑两根基准索股的横向间距和实际不符合;②虚焦点的计算方法[1]无法考虑主缆与鞍座的接触关系;③主索鞍预偏量的计算只考虑虚焦点纵向位移量,再以中跨与边跨纵向水平力是否相等作为判据,而没有考虑虚焦点在高程上的变化。只有真实的模拟主索鞍曲线进行空缆线形分析才能够解决MIDAS模型中存在的各种问题。采用精确模拟主索鞍曲线的计算方法分为两个方向:一是采用解析法模拟主索鞍找切点[2-3],二是采用有限元法模拟主索鞍与主缆的接触关系[4-5]。
1 解析法模拟主索鞍
1.1 计算假定
1)主缆为柔性结构只能受拉,且没有抗弯刚度[6];
2)主索鞍的空间圆弧曲线要求素立面圆弧和平面圆弧已知;
3)以立面圆弧最高点为界限,边跨到散索点与中跨的无应力长度已知;
4)主索鞍切点间的曲线弧长近似等于索股的无应力长度。
1.2 计算方法
空缆线形分析采用经典弹性悬链线理论,主缆的自重集度按主缆变形前的无应力长度分布。计算见图1,其解析表达式见式(1)和式(2)[7]。中跨与边跨的不平衡力决定了主索鞍圆心偏移量的大小,主索鞍的位移量与纵向不平衡力的调节由式(1)的微分增量关系进行迭代,能够得到较快的收敛,见式(3)。
(1)
(2)
(3)
式中:H,V,dH分别为空缆水平力、竖向力、边跨与中跨纵向不平衡力;q,s0,E,A0分别为空缆自重集度、计算无应力索长、弹性模量、截面面积;l,h,dl分别为计算跨径,计算高差,索鞍圆心偏移量,空缆计算见图1。

图1 空缆计算Fig.1 Hollow cable calculation chart
主索鞍曲线立面圆心与水平圆心不一定在同一里程上,因此主要以立面圆弧圆心确定切点坐标,再由散索点的坐标来分析计算跨径和计算高差,平面圆弧作为横向偏距的计算。解析法计算程序在MATLABR2013b平台编制脚本文件实现,计算步骤如下,解析迭代流程图见图2。
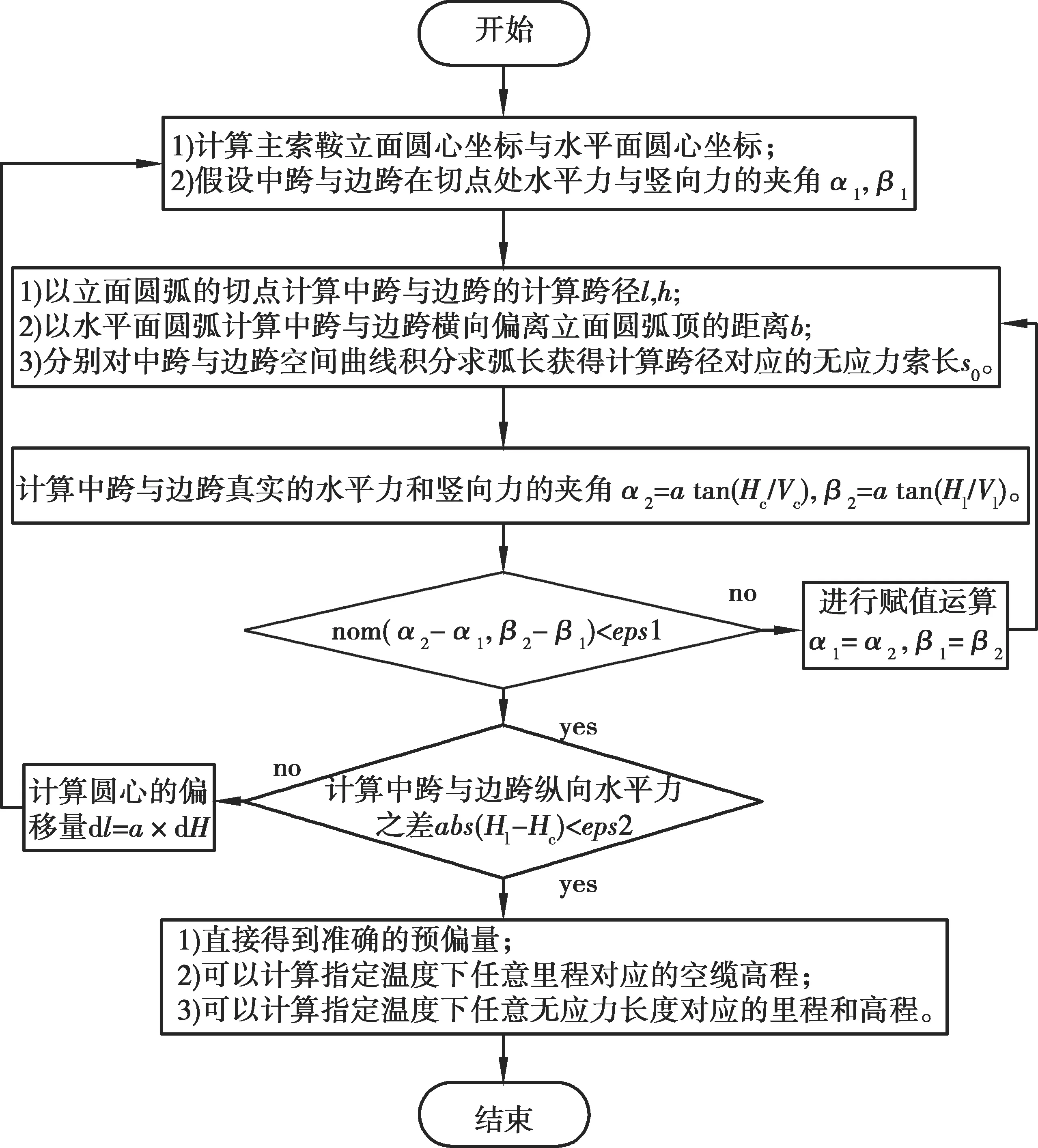
图2 解析迭代计算流程Fig.2 Analytical iterative calculation flow chart
1)根据设计图纸计算两个塔的空间主索鞍曲线立面圆心坐标和水平面圆心坐标,假设中跨切点处纵向水平力Hc和Vc之间的夹角为α1,边跨纵向水平力Hl和竖向力Vl的夹角为β1。
2)由主索鞍曲线要素计算中跨与边跨的计算跨径l,相对高差h以及切点间无应力索长s0。

4)判断α2-α1与β2-β1的二范数是否小于收敛值eps1若小于eps1计算收敛,进入步骤5)若大于eps1则赋值α1=α2,β1=β2回到步骤2)。
6)根据dH=Hl-Hc的差值由式(3)计算主索鞍圆心坐标的偏移量得到两主索鞍新的圆心坐标并进入步骤1)。
7)得到主索鞍圆心的偏移量,计算中跨和边跨在不同温度下里程对应的高程或无应力长度对应的里程和高程。
2 有限元法模拟主索鞍
2.1 计算假定
1)索股在主索鞍的索槽内横向受到刚性约束位移为0;
2)采用只受拉的杆单元能较准确地模拟主缆;
3)主索鞍的空间圆弧曲线要素平面圆弧和立面圆弧已知;
4)立面圆弧最高点为界限,边跨到散索点与中跨的无应力长度已知。
2.2 计算方法
主索鞍建模以通用有限元分析软件ANSYS作为计算平台进行分析,主索鞍的空间曲线具有精确的解析表达式,因此在模型中能够准确模拟主索鞍的位置和空间曲线长度。模拟主索鞍的悬索桥空缆线形分析主要采用了三类单元[8-9]:①只受拉的Link10杆单元模拟所有缆长;②只受压的Link10杆单元模拟主索鞍与索股的接触关系[10];③采用MPC184刚性梁单元模拟主索鞍的底座。
建模过程需要注意以下几点:
1)中跨与边跨主缆的建模长度均以已知的无应力索长控制;
2)在主缆与鞍座可能接触的地方鞍座杆单元需进行加密对应曲线长0.5~1cm可以较精确模拟主缆与鞍座的接触关系;
3)施加位移边界条件应包含散索点的回退量。
求解过程中同样以边跨与中跨的纵向水平力相等得到主索鞍圆心的偏移量,求解结束后更新模型的节点坐标即为空缆线形,见图3。

图3 有限元分析空缆线形Fig.3 Finite element analysis of hollow cable shape
3 算例分析
天河大桥北叉桥跨径为100 m+266 m+100 m双塔三跨的空间索面自锚式悬索桥。桥跨完全对称布置,主索鞍空间曲线为平面圆弧和立面圆弧的组合形式,其构造如图4,立面圆弧顶与锚箱之间的偏距为13.9 m空间性非常明显。利用文中解析法编制的脚本文件和ANSYS编写的APDL宏文件进行模拟主索鞍的空缆线形分析,考虑主塔与主梁的压缩量后计算分析所需的初始数据列于表1。
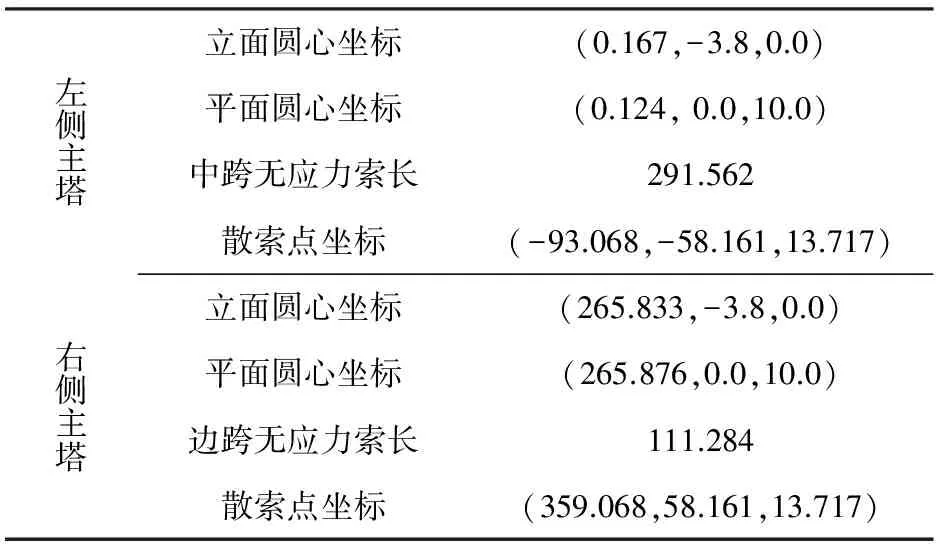
表1 初始参数
由初始参数分别用笔者介绍的解析法和有限元法得到主索鞍圆心的偏移量分别为48.4 m和48.2 m。为了对两种方法的线形进行对比将有限元分析中的主索鞍圆心强制移动48.4 m,得到解析法与有限元立面投影线形对比见图3,平面投影线形对比见图4,相对误差见图5。从分析结果可以看出解析法和有限元得到的线形计算结果十分接近,相对误差在1 mm内,两种方法的结果相互验证。

图4 主索鞍构造Fig.4 Main cable saddle configuration

图5 立面空缆线形Fig.5 Vertical hollow cable shape

图6 水平面空缆线形Fig.6 Horizontal hollow cable shape
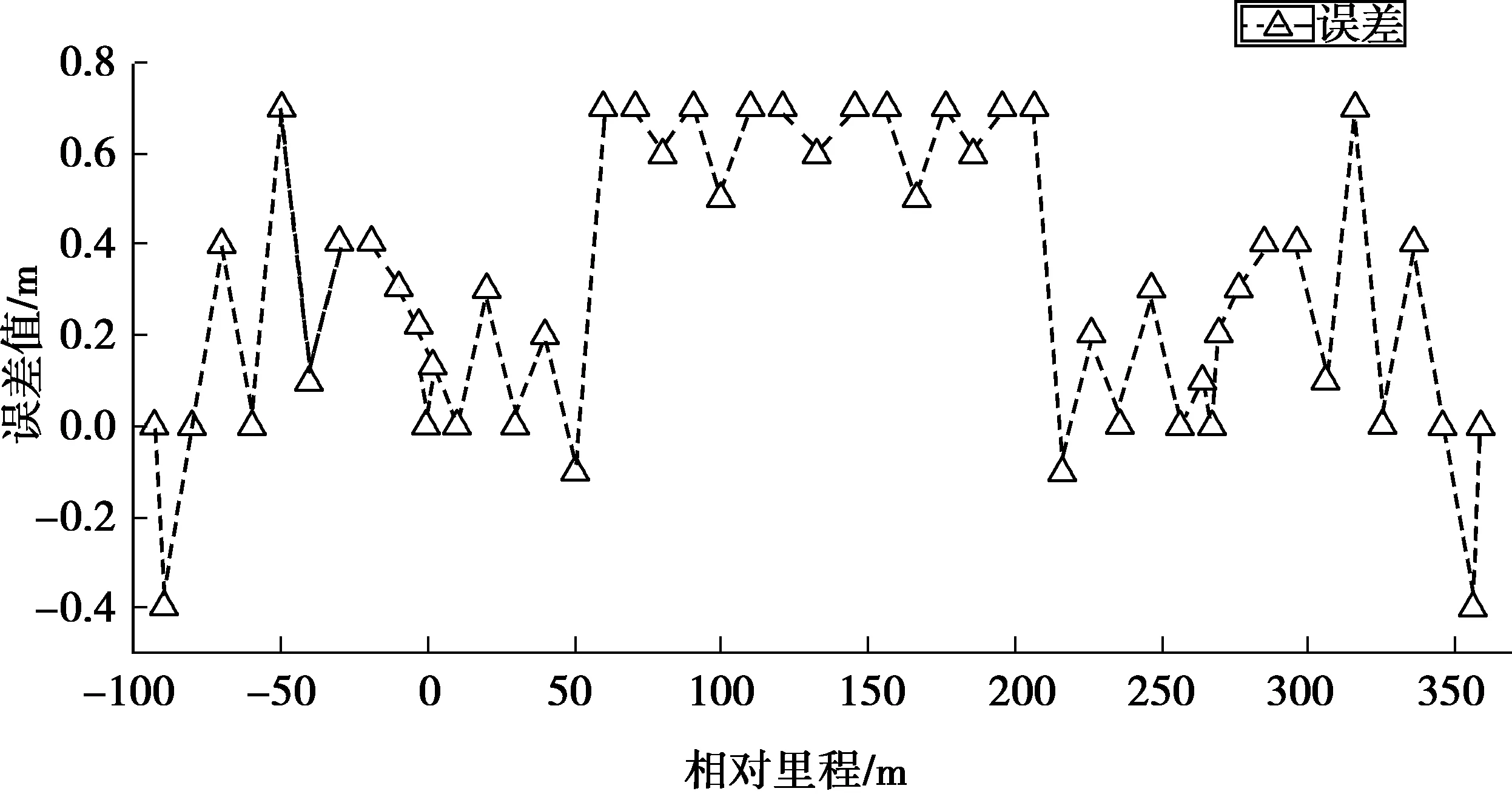
图7 解析法与有限元误差对比Fig.7 Error comparison between analytic method and finite element
4 结 语
基于弹性悬链线理论的解析法和基于ANSYS的有限单元法,同时模拟具有空间鞍座曲线的空缆架设线形分析,编制了相应的脚本文件和APDL宏文件。利用文中的程序对天河大桥双塔空间自锚式悬索桥基准索股架设进行分析,解析法和有限元法进行相互校核均能够得到较高的计算精度,可作为类似空间索面悬索桥空缆线形计算分析的两种参考方法。
[1] 黄强. 混凝土自锚式悬索桥施工控制研究[D]. 哈尔滨:哈尔滨工业大学, 2013.
HUANG Qiang.StudyonConstructionControlofConcreteSelf-anchorSuspensionBridge[D]. Harbin: Harbin Institute of Technology, 2013.
[2] 齐东春,沈锐利,郭永成. 悬索桥空间缆索线形的解析计算方法[J]. 武汉理工大学学报, 2013, 35(12): 109-113. QI Dongchun, SHEN Ruili, GUO Yongcheng. Analytical calculation method of main cable shape-finding of suspension bridge with spatial cables[J].JournalofWuhanUniversityofTechnology, 2013, 35(12):109-113.
[3] 罗喜恒. 悬索桥主缆线形的鞍座影响[J]. 公路交通科技, 2005, 22(8): 36-39. LUO Xiheng. Effect of saddle on cable shape of suspension bridges[J].JournalofHighwayandTransportonResearchandDevelopment, 2005, 22(8): 36-39.
[4] 潘永仁. 悬索桥结构非线性分析理论与方法[M]. 北京:人民交通出版社, 2004. PAN Yongren.No-linerAnalysisTheoryMethodforSuspensionBridgeStructure[M]. Beijing: China Communications Press,2004.
[5] 罗喜恒,肖汝诚,项海帆. 用于悬索桥非线性分析的鞍座-索单元[J]. 土木工程学报, 2005, 38(6): 47-53. LUO Xiheng, XIAO Rucheng, XIANG Haifan. Saddle-cable elements for nonlinear analysis of suspension bridges[J].ChinaCivilEngineeringJournal, 2005, 38(6): 47-53.
[6] 占维. 悬索桥主缆施工计算的解析迭代方法[D].武汉:武汉理工大学2007. ZHAN Wei.AnalyticalIterationMethodforMainCableConstructionofSuspensionBridges[D]. Wuhan: Wuhan University of Technology, 2007.
[7] 唐茂林. 大跨度悬索桥空间几何非线性分析与软件开发[D]. 成都:西南交通大学, 2003. TANG Maolin. 3DGeometricNo-linearAnalysisofLong-spanSuspensionBridgeandItsSoftwareDevelopment[D].Chengdu: Southwest Jiaotong University, 2003.
[8] 王新敏,李义强,许宏伟. ANSYS 结构分析单元与应用[M]. 北京:人民交通出版社, 2011. WANG Xinmin, LI Yiqiang, XU Hongwei.ANSYSStructuralAnalysisUnitandApplication[M]. Beijing: China Communications Press,2011.
[9] 王新敏. ANSYS 工程结构数值分析[M]. 北京:人民交通出版社, 2007. WANG Xinmin.ANSYSNumericalAnalysisofEngineeringStructures[M]. Beijing: China Communications Press,2007.
[10] 许琳. 悬索桥施工过程中缆索系统的精细模拟[D]. 大连:大连理工大学, 2013. XU Lin.AccurateSimulationofCableSysteminConstructionProcessoftheSuspensionBridge[D]. Dalian: Dalian University of Technology,2013.
(责任编辑 朱汉容)
Hollow Cable Shape Analysis of Suspension Bridge with Spatial Cable Plane
ZHANG Yongshui, WU Zhangxu, FENG Wei
(School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, P.R.China)
Spatial cables suspension with saddle curve has a great effect on the hollow cable shape analysis, while still analysis hollow cable shape is obtained by using the virtual focus method will be inaccurate results. Two kinds of methods were adopted to analyze the hollow cable shape with saddle effect:analytic iteration method on the saddle curve wasused to find point of tangency in analysis empty cable shape. Based on the ANSYS finite element software accurate simulation of the contact relationship of main cable and saddle was made to analysis of hollow cable shape. The calculation results of the two methods were completely consistent, both can be used as suspension hollow cable shape with spatial cables calculation method.
bridge engineering; spatial cable plane; saddle curve; hollow cable shape; analytical method; finite element
10.3969/j.issn.1674- 0696.2017.02.02
2016- 01- 03;
2016- 03-12
重庆市研究生科研创新项目(CYS16184)
张永水(1965—),男,山西临汾人,教授,主要从事桥梁工程控制理论与智能监控技术工作。Email:zhang_yongshui@163.com。
吴章旭(1992—),男,重庆人,硕士研究生,主要从事桥梁工程控制理论与智能监控技术工作。Email:13883200742@163.com。
U448.25
A
1674- 0696(2017)02- 007- 04
