基于积分滑模控制的逆变器研究
2017-03-07金爱娟郝陈祥唐新雯陈嘉林卞兆平
金爱娟,郝陈祥,唐新雯,陈嘉林,卞兆平,梅 燕
(上海理工大学 光电信息与计算机工程学院,上海 200093)
基于积分滑模控制的逆变器研究
金爱娟,郝陈祥,唐新雯,陈嘉林,卞兆平,梅 燕
(上海理工大学 光电信息与计算机工程学院,上海 200093)
滑模控制是一种基于状态空间的非线性控制方法,传统的滑模控制器,需了解所有状态的参考值,另外当跟踪信号为阶跃信号时会产生稳态误差,影响了控制器的性能。文中针对以上问题,采用了积分滑模控制器,对于逆变器系统中的参数变化敏感性较低,具有较强的鲁棒性,当系统参数突变时,系统过渡时间短、暂态性能好、稳态精度高,能实现对参考电压的快速准确跟踪。
积分滑模控制;逆变器;鲁棒性
在对逆变器进行建模和控制时,逆变器所带负荷通常是复杂多变的[1]。要保证逆变器快速准确地跟踪参考信号,就要求控制器对时变的负荷以及参数的摄动,具有良好的动静态性能和鲁棒性。滑模控制是一种基于状态空间的非线性控制方法,不需要精确的对象模型,对被控对象的模型误差、对象参数的变化以及外部干扰具有较强的鲁棒性[2]。传统的滑模控制器,需要了解所有状态的参考值。另外,当跟踪信号为阶跃信号或者任意信号时会产生稳态误差,影响了控制器的性能。而对于积分滑模乃至二重积分滑模控制器,对逆变器系统中的参数变化敏感性较低,具有较强的鲁棒性,同时对于负荷干扰变化具有较好的动静态性能,能够实现对参考电压的快速准确的跟踪。本文采用SVPWM技术来控制三相逆变器,在此基础上给出了三相逆变器基于d-q旋转坐标下的滑模控制的控制模型和基于d-q旋转坐标下的积分滑模控制的控制模型。对比分析在这两种不同控制方法下电路的输出性能,证明了积分滑模控制具有的优越性。
1 滑模控制的三相逆变器
逆变器控制多采用脉宽调制(PWM)技术,除应用于逆变电路,还应用于其他电力电子电路中,其中主要应用于直流斩波电路和整流电路中。磁链追踪型PWM法(SVPWM)技术最先用于交流变频调速系统中,利用SVPWM控制的电路具有优良的动态性能。
在矢量控制的三相逆变电路中,通常需要进行一些坐标变换,将输出三相交流电流ia,ib,ic转换为d-q坐标系下的两相直流电流id和iq;将输出三相交流电压ua,ub,uc转变为d-q旋转坐标系下的两相直流电压ud和uq。其转化关系如下所示
(1)
(2)
本文所采用的三相逆变器具体的电路图如图1所示,其中R的值为1 Ω,LA=LB=LC=3 mH,Ca=Cb=Cc=1 200 μF,Vd=600 V。

图1 三相逆变器的主电路图
要使三相逆变器的输出具有好的鲁棒性,并能满足在载波频率变化的情况下,也能具有稳定的输出,一般可使用滑模控制。相对于其他的非线性控制方法而言,滑模控制是比较好实现的,在进行滑模设计时,需要选择合适的滑模面。当然,滑模控制根据不同的被控电路,其具体的控制电路也是不同的,由图1可得到三相逆变主电路的状态方程表达式如下
(3)
式中,iL为电感电流;VC为电容两端电压;Vd为输入电压,其中,Uo为R0两端电压,将上述等式写为d-q轴上的表达式如下
(4)
选择电感电流和输出电压为状态变量,即有x1=U0;x2=iL。此时,可得到S函数如下
S=α1x1+α2x2
(5)
(6)

(7)
同理可得
(8)
由上述等式(3)~式(6)可得到如下的三相逆变电路的控制框图。
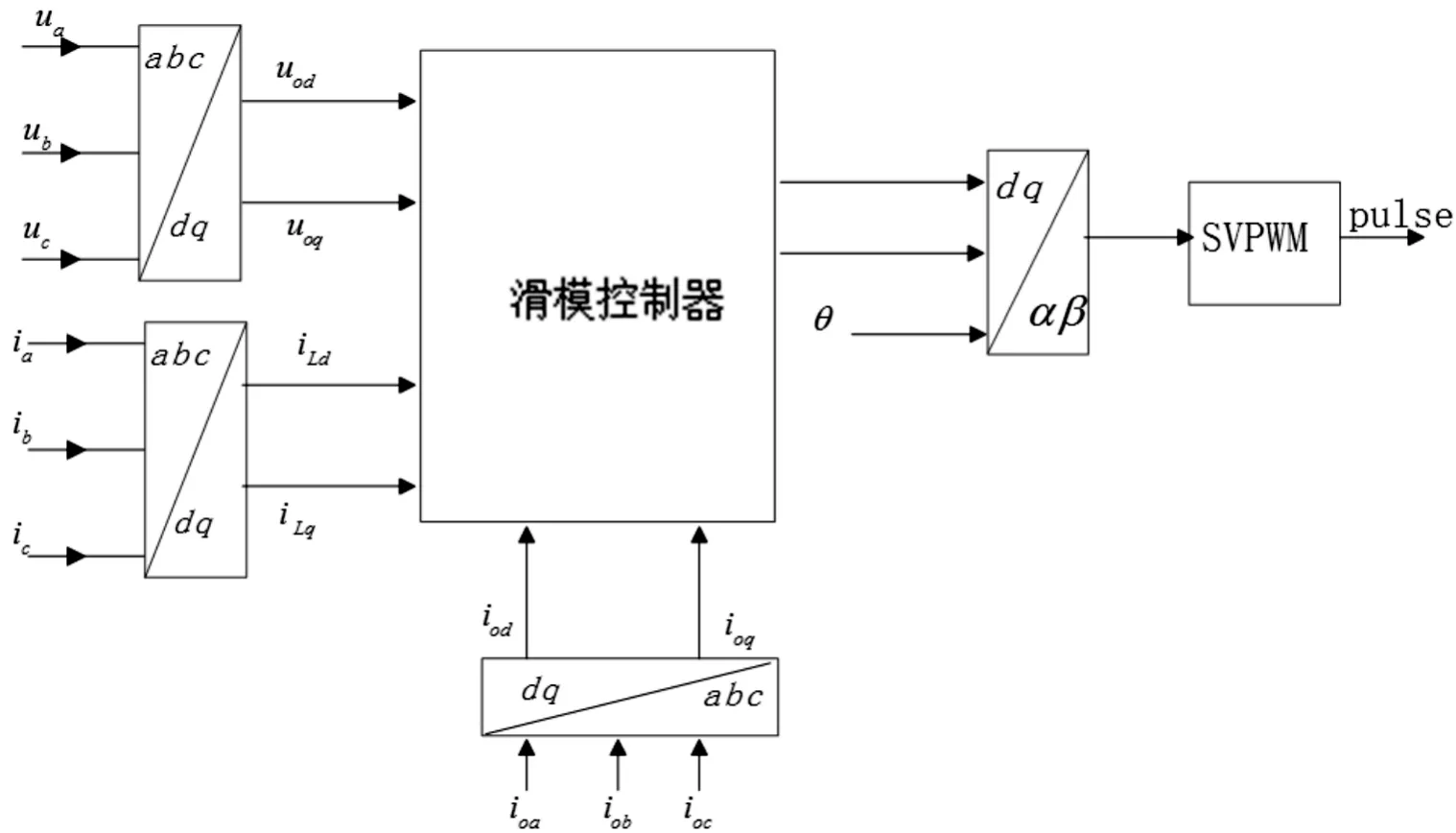
图2 滑模控制下三相逆变器总框图
在图2中,在该控制器中,反馈信号为ua,ub,uc,ia,ib,ic以及ioa,iob,ioc,经过坐标转换,得到d-q坐标轴上的电信号,再经过滑模控制器,其输出信号再经过坐标转换及SVPWM调制,得到6路PWM脉冲,用来控制逆变器。图3为滑模控制器具体框图,其中,dd和dq为控制器输出信号,这两个信号经过坐标变换后的输出信号通过SVPWM调节,得到PWM脉冲。

图3 滑模控制器框图
图3中函数f1和f2的表达式分别为
(9)
(10)
在上述控制算法下,给出电路中各参数如下,LA=LB=LC=3 mH,CA=CB=CC=1 200 μF,R0=20 Ω,α1=α2=1,ε=6×105,开关频率f=20 kHz当K值不相同时,其中输出电压幅值的参考值为311 V,通过仿真可给出如表1所示的仿真结果。
(1)借鉴吸收会聚理论,完善我国科技创新思想体系。美国科技界对会聚研究的长期战略思考及实践,值得我国科技界高度关注和重视,并围绕科技创新会聚趋势和举措开展研究。结合我国科技创新和科技体制改革的最新实践,进行前瞻性的科技创新理论研究,进一步丰富我国科技创新战略思想体系。

表1 滑模控制下仿真结果
上表是电路运行在稳定状态时在同一时刻取到的值,由上表可看到,在K值取到较大时,即k1,k2的取值较小时,输出电压的谐波失真能达到较小,并在k1=-60 000时,谐波失真达到最小,此后再减小则始终保持不变,但输出电压在50 Hz时候的基波幅值却在k1=-120 000时才达到理论值311 V,而k1的绝对值越大,则对器件的要求越高,若k1的绝对值取得较小,由仿真结果可看到,此控制器控制的逆变器输出存在很大的稳态误差。
2 积分滑模控制器的设计与仿真
上文设计的滑模控制器,虽然三相逆变电路的输出电压很难达到参考值311 V,但该方法在调节合适的K值情况下,电路输出电压的总谐波失真指数能得到有效地降低。根据仿真结果,证明了该滑模控制方法部分有效,为了减小输出电压基波幅值误差,可研究带积分项的滑模控制器在三相逆变电路中的应用。在文献[3]中研究了积分谐振滑模控制器在三相逆变电路中的应用,该文章中采用准滑动模型的控制器,并给出了相应的积分项。在上述文献的基础上,本文对积分项进行了改进,选用输出电压和电感电流作为状态变量,并给出积分项表达式(11),结合图1所示的逆变器主电路图,采用上文中所提到滑动模型,可得到具体的控制模型。
为减小电路输出电压基波幅值的稳态误差,在此给出两个积分项,可得到 函数如下

(11)
其中,x1=U0;x2=iL,同样有
(12)

(13)

(14)


表2 滑模控制下三相逆变器各仿真参数
根据表2中的数据,得到如图4和图5所示的仿真结果。

图4 积分滑模控制下输出电压仿真波形
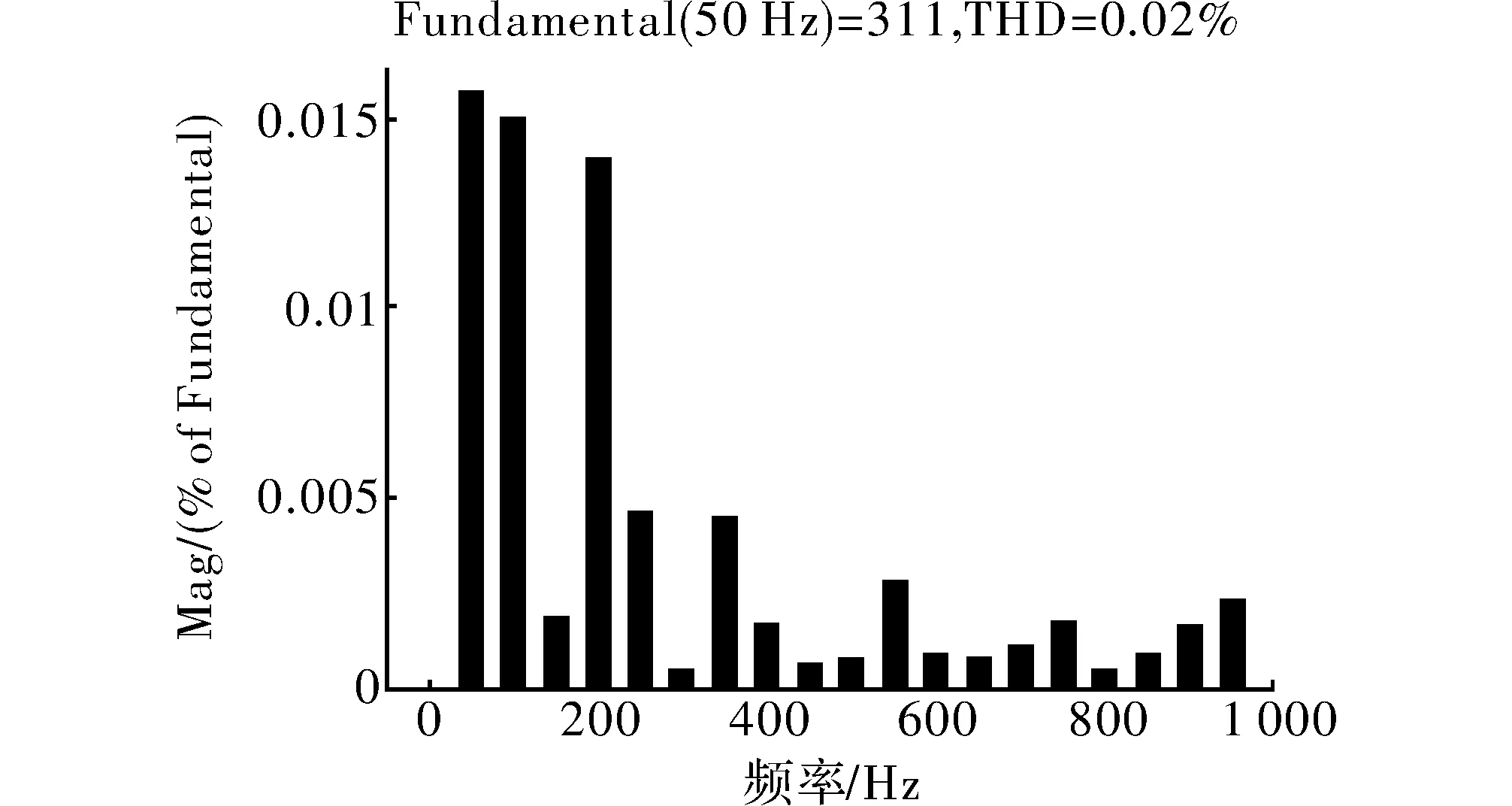
图5 积分滑模控制下输出电压FFT分析图
由图4可看到,输出电压是逐渐达到稳定状态,且输出是极其稳定的。
3 积分滑模控制的特性分析
积分滑模控制下的三相逆变电路在 较小时,其输出电压基波幅值便能达到311 V,较滑模控制下的三相逆变电路的输出要稳定得多,说明了所设计的积分滑模控制器的正确性,为了进一步的探讨文章中所设计的积分滑模控制器的特性,在下文中,将会讨论在k1值发生变化时,而其他参数均不变时的电路输出特性,以及在载波频率发生变化时电路输出特性。通过对电路输出电压变化曲线的分析,可容易地找到电路在该控制方式下各参量最合适的参数值。
由FFT频谱分析图可知,当采用所设计的积分滑模控制时,当系统达到稳定时,基波频率幅值为311 V,这个值等于系统设定的参考值,说明所给出的积分项在整个控制器中起到了良好的效果,此时整个逆变电路的总谐波失真(THD)只有0.02%,总的谐波失真微小。按照行业标准,当逆变器输出为正弦波时,总谐波失真要≤5%,本文设计的控制方法理论上输出的谐波失真远小于这个值。
在上述控制中,对于图5所示的仿真结果,是在k1一定,载波频率一定的情况下得到的仿真结果,根据表2中各仿真参数,可得到图5的仿真结果是在k1=-45 000且载波频率为20 kHz时得到的结果。下文将会探讨当k1的值发生改变时,电路的输出电压基波幅值和输出谐波分量大小情况,同时还会给出当k1值一定,电路载波频率发生改变时,电路输出电压基波幅值和输出谐波分量大小情况。
表3给出了k1变化时输出电压的各参数变化情况。由表可知,k1的绝对值越大,电路的输出谐波失真指数越小,同样地,在k1=-60 000的时候总谐波失真达到最小,不管k1的值怎么变化,输出电压的基波幅值均在311 V附近,采用所设计的积分滑模控制器有效地解决了滑模控制器控制中提到的基波幅值很难达到311 V的缺点。
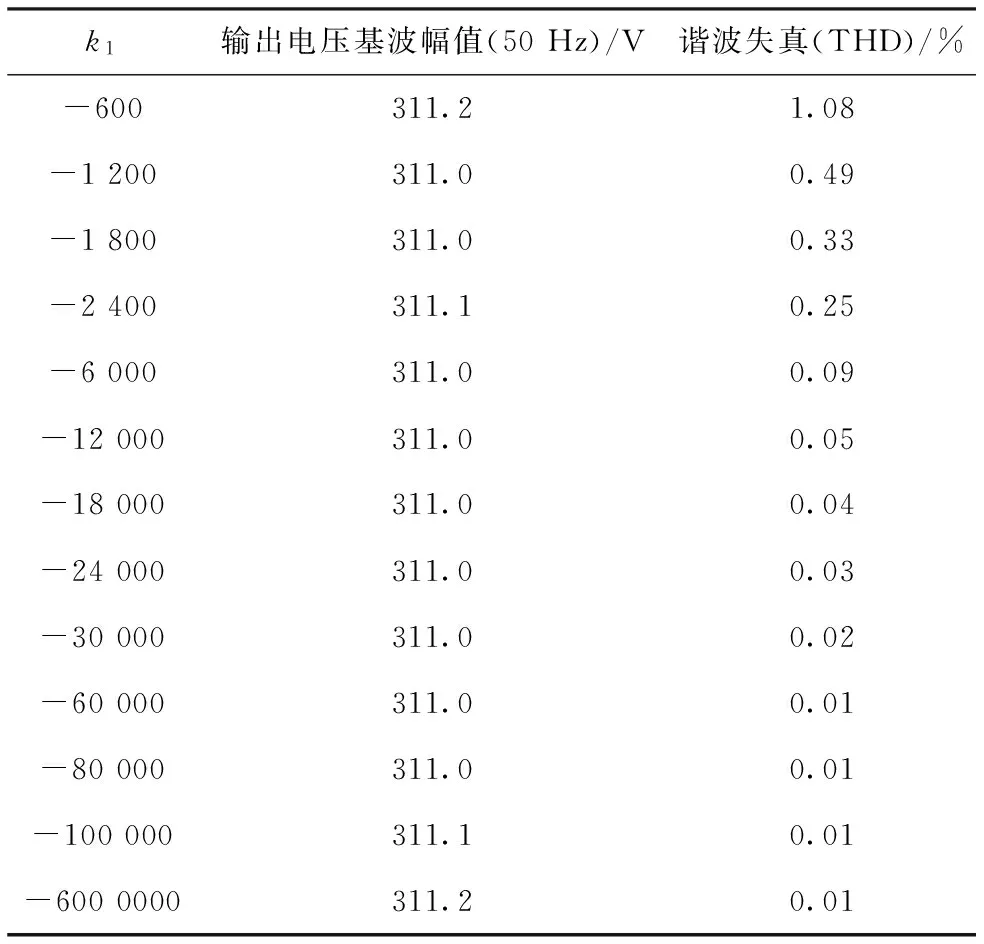
表3 k1变化时输出电压基波幅值与谐波失真
本文中设计的积分滑模控制,不仅能很好地使电路的输出电压基波幅值达到理想参考值,在开关频率变化的情况下,该输出依然能够达到稳定状态,在k1为-600时,电路其他参数如表2所示,给出如图6和图7所示的曲线图。

图6 基波幅值变化曲线图
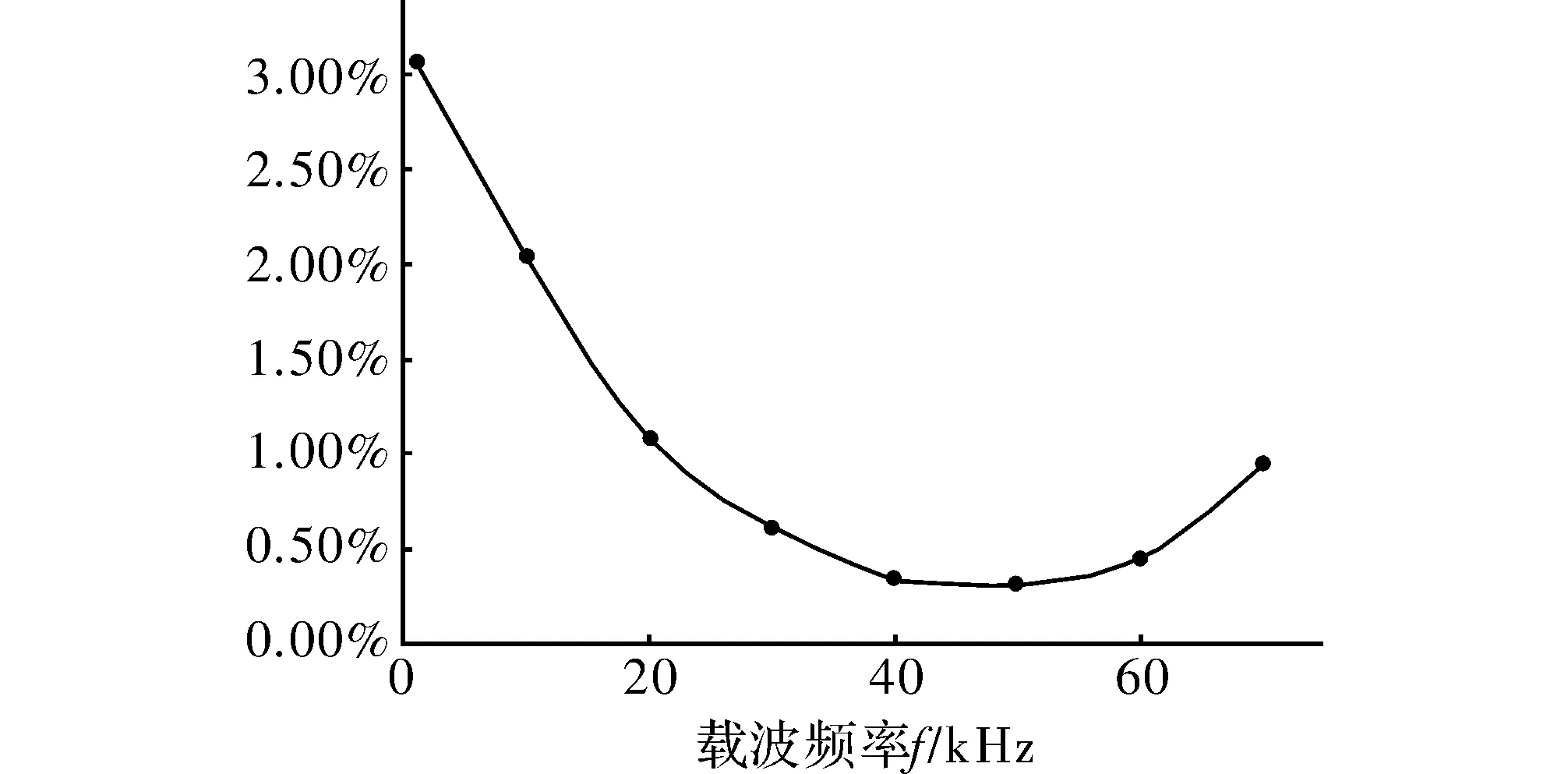
图7 谐波失真指数变化曲线
在图6和图7中,频率由1~70 kHz变化时,输出电压的基波幅值在311 V处上下波动,且误差均较小,最大误差不超过0.5 V,而输出电压总谐波失真则是随着频率的增加而减小,在超过70 kHz后,总谐波失真THD则是随着载波频率的增加而变大。
4 结束语
针对文中给出的逆变电路选择了状态变量,采用传统的滑模控制方式,由仿真结果可得到,逆变电路在该控制算法下虽输出谐波分量较小,但基波幅值难达到理想值。针对其的缺点给出了积分滑模控制算法,该控制方法在滑模控制的基础上加入了两个积分项,结合文中所选用的趋近律以及电路的状态方程给出了具体的控制算法,通过仿真实验,给出了上述控制算法分别在不同载波频率下和不同k1值下电路输出基波幅值和总谐波失真情况,仿真实验证明了文中所设计的控制方法的可行性。该控制算法不仅解决了滑模控制中电路基波幅值很难达到理想值的缺点,同时也解决了电路输出在载波频率变化较大时输出不稳定的问题。验证了所设计的控制方法的正确性。
[1] 屈百达,潘文英.三相逆变器的建模及其控制[J].电源技术,2014,38(2):345-348.
[2] Lei J,Su S,Liu G,et al.The sliding mode control method of grid-connected inverter applied to three-phase intermittent power supply [C].Beijing: Proceedings of the 29th Chinese Control Conference,2010:4885-4888.
[3] Hao X,Yang X,Xie R. A fixed switching frequency integral resonant sliding mode controller for three-phase grid connected photovoltaic inverter with LCL-filter [C].Melbourne,VIC:CCE Asia,2013:793-798.
[4] 周锦荣,王辉,周小方.三相逆变电源系统的SVPWM技术研究[J].宁夏大学学报:自然科学版,2013,34(4):
317-320.
[5] 马静,郭锐,王玉慧,等.基于积分滑模控制的广域阻尼鲁棒控制策略[J].电网技术,2013,37(2):362-366.
[6] 李鹏,郑志强.非线性积分滑模控制方法[J]. 控制理论与应用,2011,28(3):421-426.
[7] 李鹏.传统和高阶滑模控制研究及其应用[D].长沙:国防科学技术大学,2011.
[8] 全宇,年珩.不平衡及谐波电网下并网逆变器的谐振滑模控制技术[J].中国电机工程学报,2014(9):1345-1352.
[9] 尚磊,孙丹,胡家兵,等.三相电压型并网逆变器滑模变结构直接功率控制[J].电力系统自动化,2010,34(14):79-83.
[10] 王兆安,刘进军.电力电子技术[M].4版.北京:机械工业出版社,2008.
[11] 陈智勇,罗安,陈燕东,等.逆变器并联的自适应滑模全局鲁棒电压控制方法[J].中国电机工程学报,2015,35(13):3272-3282.
[12] 李政,胡广大,崔家瑞,等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014(3):431-437.
[13] 张晓光,孙力,赵克.基于负载转矩滑模观测的永磁同步电机滑模控制[J].中国电机工程学报,2012,32(3):111-116,8.
[14] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用,2007(3):407-418.
[15] 郑雪生,李春文,汤洪海,等.三相PWM电压型逆变器的积分滑模控制[J].电工技术学报,2007,22(12):105-109.
[16] 陈江辉,谢运祥,公伟勇,等.新型单Buck逆变器三阶积分滑模控制策略[J].电力自动化设备,2010,30(9):33-37.
Research on Inverters Based on Integral Sliding Mode Control
JIN Aijuan,HAO Chenxiang,TANG Xinwen,CHEN Jialin,BIAN Zhaoping,MEI Yan
(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
Sliding mode control is a nonlinear control method based on the state space. The traditional sliding mode controller requires knowledge of the reference values of all states, and step tracking signals lead to steady-state errors, thus affecting the controller performance. In this paper, the integral sliding mode controller is proposed, which is less sensitive to parameter changes in the inverter system and of good robustness. When the system parameters mutation system transition time is short, it offers good transient performance and high steady precision, thus realizing quick and accurate tracking of the reference voltage.
integral sliding mode control; inverter; robustness
2016- 03- 22
金爱娟(1972-),女,博士,副教授。研究方向:电力电子非线性及控制。
10.16180/j.cnki.issn1007-7820.2017.02.021
TM 46
A
1007-7820(2017)02-079-05
