基于降落序列影像的嫦娥三号着陆轨迹恢复
2017-03-07徐辛超徐爱功刘少创马友青
徐辛超,徐爱功,刘少创,马友青
(1.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000;2.中国科学院遥感与数字地球研究所,北京 100101)
基于降落序列影像的嫦娥三号着陆轨迹恢复
徐辛超1,2,徐爱功1,刘少创2,马友青2
(1.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000;2.中国科学院遥感与数字地球研究所,北京 100101)
针对传统方法进行着陆器降落轨迹恢复的精度较低或者算法过于复杂的问题,提出一种基于降落序列影像的着陆器轨迹恢复方法:首先采用SIFT方法进行序列影像间特征点的提取与匹配,然后利用得到的匹配点进行影像间的相对定向,最后结合降落相机和影像的相关参数等得到最终的着陆轨迹。采用嫦娥三号真实影像抽稀后开展了实验,结果表明该方法的实现过程简单且轨迹恢复结果与探月工程预期设计目标基本一致,证明提出的方法能够有效完成着陆器轨迹的恢复。
嫦娥三号;降落相机;降落影像;轨迹恢复;特征匹配
0 引言
我国探月二期工程已经取得了圆满成功,在此期间,着陆器和巡视探测器获取了大量的影像,为后续的导航定位等服务提供了更好的基础[1]。着陆器的位置在探月二期任务中具有重要的作用,是巡视探测器导航定位的参考点,后续的路径规划等任务都以它为参考点展开[2]。着陆器携带的降落相机在下降过程中以不低于10帧/秒的速度拍摄了大量影像,此外,还有嫦娥一号的X频段 (unified X-band,UXB)与甚长基线干涉测量(very long baseline interferometry,VLBI)观测数据等都可以为着陆器的定位提供服务。
目前,着陆器的定位方法主要有基于摄影测量的方法和基于遥测信号的方法2大类。基于遥测信号的定位方法中:文献[3-4]基于现有测控条件,从跟踪弧段和测量数据组合2个方面开展定位,得到优于100 m的定位精度;文献[5]通过基于地基观测量的运动学统计定位方法,实现了精度优于50 m的定位结果。显然,上述基于遥测信号的方法定位结果精度较低。基于摄影测量的方法中:文献[6]提出了一种基于图像序列的月球着陆器着陆点定位计算方法;文献[7]利用降落影像序列实现嫦娥三号系统着陆点高精度定位;文献[8]利用搜索法实现了对巡视器和着陆器的相对位置的确定。但以上基于图像的定位方法均实现的是单点定位,而没有实现着陆轨迹的恢复。文献[9-10]研究了通过光束法进行嫦娥三号着陆器轨迹及姿态高精度恢复的方法;但是光束法求解过程中参数较多,求解过程较为复杂。
由于着陆后的定位导航都以着陆器本体坐标系作为参考,因此本文提出了一种针对垂直降落阶段的、基于降落序列影像的着陆器轨迹快速恢复方法。
2 着陆轨迹快速确定方法
2.1 降落影像分析
嫦娥三号着陆器在降落过程中,其底部安装的降落相机拍摄了大量的影像,为后续巡视探测器的导航定位及着陆区的地形重建等工作提供了基础数据。
着陆器下降过程主要分为主减速段、接近段、悬停段、避障段和缓速下降阶段。主减速段高度为15 km,接近段高度为2 km,悬停阶段的高度为100 m,避障段的高度为100至30 m,缓速下降阶段高度为30至3 m,3 m以后的阶段为自由落体。降落影像的拍摄过程主要是在着陆器的接近段、悬停段、避障段、缓速下降段,全程约690 s。图1为着陆器降落过程示意图。
降落相机拍摄频率为10帧/秒。由垂直降落过程拍摄的降落影像可以得出,相邻影像间的平均重叠度接近99 %。为了减少计算的数据量,本文在计算的时候选择每隔10幅影像进行采样,得到平均重叠度约为95 %的30幅影像,采用稀疏后的降落影像序列开展着陆轨迹恢复。
2.2 降落影像相对定向
相对定向主要是完成2幅影像的相对位置和姿态[11];由2幅降落影像的相对位置即可得到相对降落轨迹。
假设取不同高度拍摄的2幅降落影像建立立体模型,选择高度较高的影像(下文中称为左像)的像空间直角坐标系S1X1Y1Z1作为参考系统,原点为其摄影中心S1,X1轴平行于影像的行方向,Y1轴平行于影像的列方向,Z1轴与X1Y1构成右手系。图2为S1X1Y1Z1坐标系统示意图。假设另一降落影像(下文中称为右像)的摄影中心为S2,则可以建立新的空间直角坐标系统S2X2Y2Z2,各坐标轴方向与S1、X1、Y1、Z1类似。在参考系统S1X1Y1Z1下,S2相对于S1的平移量为B,其在3个坐标轴方向的分量分别为BX、BY、BZ,3个坐标轴方向的转角分别为φ、ω和κ,以上6个元素称为相对定向元素。假设地面点A在左右像中的同名像点分别为P1和P2,对应的像点坐标分别为(x1,y1)和(x2,y2),在各自的空间直角坐标系下对应的坐标分别为(X1,Y1,Z1)和(X2,Y2,Z2),结合S1、S2则有图2所示的几何结构。
由图2可得,向量S1S2、S1P1和S2P2是共面的,于是可以得出

(1)
式中(X1,Y1,Z1)和(X2,Y2,Z2)无法直接获取,而是通过其对应的像点坐标求得,其与像点坐标有以下的对应关系为:
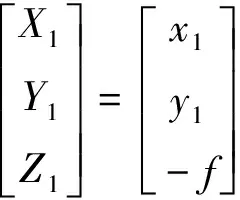
(2)

(3)
式中:f为相机焦距;R为3个旋转角组成的旋转矩阵。
相对定向过程中6个相对定向元素为待求解的参数。像点坐标可以从降落影像中直接获取,可以将式(2)、式(3)代入式(1)中,得到关于相对定向元素的方程。令其为F,很显然为一个非线性方程,需要经过线性化以后才能进一步求解。将F展开并取至一次项可以得出

(4)
由式(4)可知:需要至少组成6个以上的方程组才能完成求解,而通过降落影像直接获取的观测量为同名像点的像点坐标。因此,需要提取至少6对以上的同名像点,才能够完成相对定向元素的计算。垂直降落阶段获取的降落影像平移量很小,而且坐标轴的旋转角度也较小,因此,可以取BX、BY为0。BZ为2幅影像间的垂直高差,可以利用激光高度计数据得到,3个旋转角都比较小,其初值都可以取0。利用上述初值,结合式(4),通过迭代即可完成相对定向元素的求解。
2.3 算法实现流程
算法的具体实现过程如下:
1)进行相邻降落影像间的特征点提取与匹配。由于影像间存在尺度缩放,因此,本文采用了经典的SIFT方法进行特征点的提取和匹配[12]。
2)利用提取的特征点对以及相机的像素大小、像主点坐标等参数,将匹配点坐标转换为像平面直角坐标系下以mm为单位的像点坐标。
3)根据3个旋转角元素初值计算式(3)中的旋转矩阵R的各个元素。
4)根据像点坐标、相机焦距以及旋转矩阵R计算同名像点在参考坐标系下的坐标(X1,Y1,Z1)和(X2,Y2,Z2)。
5)根据步骤4)中计算的数据并结合BX、BY和BZ的初值组成方程组,求解得到新的6个方位元素初值。
6)判断计算得到的方位元素新值与初值之间的差值,如果满足迭代要求则停止迭代,认为该方位元素为最终的方位元素;如果不满足条件,则利用新的方位元素,重新进行步骤3)~5)的操作,直到满足迭代停止条件,得到最终的方位元素。
7)选择开始垂直降落的第1幅影像与下一幅影像计算相对定向元素,根据下一幅影像相对于第一幅方位元素中的BX、BY和BZ计算着陆轨迹,即3个坐标轴方向的偏移量。
8)结合相机参数和影像高度,确定像元大小与实际地面大小的对应关系,将相对定向元素转换为实际意义上的距离[9]。
9)进行后续影像相对定向元素的计算,得到相对于上一幅影像的偏移量,并通过累加得到相对于第1幅影像的相对位移。以此类推得到后续影像相对于第1幅影像的相对位置,并参考步骤8),转换为实际意义上的位移,从而得到最终的垂直降落阶段的轨迹。
3 轨迹恢复实验与分析
为了对提出方法进行验证,采用嫦娥三号精避障及后续阶段的降落影像进行了实验,并得到了以像素为单位的相对位移。由于嫦娥三号的降落影像是10帧/秒,而且相邻影像重叠度较高,因此,为了简化计算,实验时每隔10幅提取一幅影像作为实验影像,共30幅。由于着陆器下方的设备一直存在于降落影像中,因此,需要通过掩膜将其处理后再进行特征点提取和后续匹配及相对定向。图3为垂直降落阶段的第1、第11幅影像及掩膜。
首先采用经典SIFT方法进行特征匹配,取阈值为0.2,搜索范围为50个像素,与核线距离误差为1个像素时的特征点匹配结果如图4所示。为了保证匹配结果的有效性,需要采用掩膜将着陆器降落架部分去掉,即将位于掩膜区域内的匹配点剔除,剩余的匹配点才可以参与相对定向运算。
由图4可以得出:除去着陆器设备外的影像重叠区内存在分布较为均匀的匹配特征点,可以作为后续的相对定向过程的起算数据。
降落相机焦距为8.594 mm,像幅大小102 4个像素×102 4个像素,像素大小为6.7 um,像场角为45.4°×45.4°,结合得到的匹配点坐标,根据式(4)建立对应的方程组,并进行迭代求解,得到剩余29幅降落影像相对于第1张影像在3个坐标轴方向的偏移量。假设悬停后开始降落的高度为91 m(见文献[10]),则根据相机参数,可以计算得到第1幅影像中每个像元对应地面的实际大小为0.071 m,结合相对定向过程可以得到每对影像间的以m为单位的相对位移。图5为着陆器分别在XY平面方向上相对于上幅影像的偏移量。
由图5可以得出,X方向的最小相对位移为第29幅和第30幅影像间的0.010 m,最大相对位移为第7幅和第8幅影像的0.126 m。Y方向的最小相对位移为第29幅和第30幅影像间的0.014 m,最大相对位移为第9幅和第10幅影像的0.198 m。可见,在精避障及后续阶段,为了获取最佳着陆点,着陆器在XY方向都进行不同程度的调整,但是X方向的最大调整小于Y方向的调整。这与在着陆区地形中,着陆点需要选择在既能安全着陆又具有一定地质研究意义的点位的要求相吻合。
通过比较可知:文献[7]首先采用SIFT进行特征点提取,然后进行2幅图像的镶嵌,最后通过导航相机的立体交会将结果转换为实际的月球坐标系下的单一着陆点的位置;而本文采用SIFT进行特征提取,结合相对定向理论,实现影像间的相对定向,并得出6个相对定向参数,然后结合降落影像的高度数据将相对定向结果转换为具有实际意义的着陆轨迹。文献[7]的目的是得到着陆点在月面的经纬度坐标;而本文方法侧重的是得到垂直降落阶段的降落轨迹,即每幅降落影像相对于悬停阶段后第一幅降落影像的位移。为了研究整体的着陆轨迹,本文对降落过程的累积位移进行了研究。图6为平面方向累积位移结果。
由图6可以看出X方向和Y方向的整体着陆轨迹较为平稳,其中Y方向累积位移为2.769 m,X方向的累积位移为1.633 m,Y方向的调整大于X方向的调整。从着陆轨迹可以得出,Z方向的最小相对位移为第1幅和第2幅影像间的0.181 m,最大相对位移为第11幅和第12幅影像的7.794 m。由Z方向的相对位移可以得出,着陆器在降落过程中,第1~12幅影像的相对高差增大,第12幅影像后相对高差逐渐减小。这主要是由于着陆器由悬停阶段开始降落时,速度逐渐增大,第11~12幅影像时增加到最大,后续过程中减速发动机开启,逐渐将速度降低,到30 m高度附近时着陆点基本选定,完成精确避障任务。至30 m以下的高度,进入缓速下降阶段,速度基本恒定,平面方向位移很小,与预期设置目标基本一致。
图6的整体着陆轨迹中,100至30 m的精确避障阶段,速度先增大后减小,到30 m附近时水平方向的速度基本为零。30~20 m的过程中还存在较缓慢的减速过程,20~4 m的下降阶段,着陆器基本以较小的速度匀速降落。降落轨迹在本次实验阶段预期设置目标为:着陆点上方30 m前确定最佳着陆点,且水平方向速度为零,30~4 m的阶段要以较小的速度匀速垂直下降,基本消除水平速度和加速度。上述实验数据表明采用提出方法确定的着陆过程轨迹与预期设置目标基本吻合,证明本文提出的着陆轨迹恢复方法是有效的。
4 结束语
本文在对垂直降落阶段的成像过程及降落影像特征进行充分研究的基础上,提出了一种基于序列影像的着陆器轨迹恢复方法。首先采用经典SIFT方法进行特征点提取和匹配;然后利用匹配点进行2幅图像间的相对定向,得到相对定向元素,结合相机参数计算像元大小与实际地面大小的对应关系;最终将相对定向元素转换为具有实际意义的相对位移,通过相对位移累积即可得到着陆轨迹。采用真实的嫦娥三号降落影像对提出的方法进行了验证,实验结果表明,采用提出的方法获取的着陆器在垂直降落阶段的着陆轨迹与嫦娥三号真实预期设置基本吻合,从而证明了所提出的方法的有效性。本文提出的方法可以为我国后续的深空探测提供一定的参考。
[1] 闫凯,欧阳自远.嫦娥三号:登月![J]科学世界,2013(9):8-13.
[2] 欧阳自远,李春来,邹永廖,等.绕月探测工程的初步科学成果[J].中国科学:地球科学,2010,40(3):261-280.
[3] 曹建峰,胡松杰,张宇,等.嫦娥三号着陆器统计定位精度分析[J].飞行器测控学报,2014,33(3):244-249.
[4] 曹建峰,张宇,胡松杰.嫦娥三号着陆器精确定位与精度分析[J].武汉大学学报·信息科学版,2016,41(2):274-278.
[5] 李培佳,黄勇,昌胜骐,等.基于地基观测的嫦娥三号着陆器与巡视器高精度定位[J].科学通报,2014,59(32):3162-3173.
[6] 徐焕宇,刘佶鑫,孙巍巍,等.基于序列图像的月球着陆定位计算方法研究[J].计算机科学,2011,38(12):269-273.
[7] 贾阳,刘少创,李明磊,等.利用降落影像序列实现嫦娥三号系统着陆点高精度定位[J].科学通报,2014,59(19):1838-1843.
[8] 昌胜骐,黄勇,刘庆会,等.利用搜索法对嫦娥三号着陆器和巡视器定位[J].宇航学报,2015,36(6):624-629.
[9] 刘召芹,万文辉,彭嫚,等.遥感制图与导航定位技术在嫦娥三号遥操作中的应用[J].遥感学报,2014,18(5):971-980.
[10]刘斌,徐斌,刘召芹,等.基于降落相机图像的嫦娥三号着陆轨迹恢复[J].遥感学报,2014,18(5):981-987.
[11]柯涛,张祖勋,张剑清.旋转多基线数字近景摄影测量[J].武汉大学学报·信息科学版,2009,34(1):44-51.
[12]LOWE D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
Landing trajectory restoration of Chang’e-3 based on descent images
XUXinchao1,2,XUAigong1,LIUShaochuang2,MAYouqing1
(1.School of Gematics,Liaoning Technical University,Fuxin,Liaonng 123000,China; 2.Institute of Remote Sensing and Digital Earth,Chinese Academy of Sciences,Beijing 100101.China)
Aiming at the problem that the precision of Very Long Baseline Interferometry method is poor and other photogrammetry algorithms are too complex,the paper proposed a method of trajectory restoration based on the descent images:firstly,extraction of feature points and feature matching were carried out by SIFT method,and the relative orientation of the images was completed using the obtained matching points,fianlly the final landing trajectory was obtained by combining the correlation parameters of the landing camera and the images.The experiment was carried out on the real descent images of Chang’e-3 lander.Results showed that the proposed method would have simple processing and good landing trajectory restoration results consistent with the expected design goals of lunar exploration program,which proved that it could effectively accomplish the trajectory restoration of the lander.
Chang’e-3;landing camera;descent images;trajectory restoration;feature matching
2016-08-09
国家重点研发计划项目(2016YFC0803102);国家自然科学基金项目(41401535)。
徐辛超(1984—),男,山西汾阳人,博士,讲师,研究方向为空间大地测量数据处理和摄影测量。
徐辛超,徐爱功,刘少创,等.基于降落序列影像的嫦娥三号着陆轨迹恢复[J].导航定位学报,2017,5(1):8-11,17.(XUXinchao,XUAigong,LIUShaochuang,etal.LandingtrajectoryrestorationofChang’e-3basedondescentimages[J].JournalofNavigationandPositioning,2017,5(1):8-11,17.)DOI:10.16547/j.cnki.10-1096.20170103.
P
A
2095-4999(2017)01-0008-05
