整体观照 厘清序列
2017-03-07侯军波周春萍
侯军波+++周春萍
【摘 要】除法教学是小学计算教学的一块基石,要有效突破除法教学的难点,必须在整体观照的理念下厘清知识序列,精心处理好前置性教学的内容。就“同数连减解决问题”的教学而言,它在整个序列的推进中起到了承上启下的作用,通过“依托课始孕伏,唤醒知识储备;梳理核心策略,助力模型建构;抓住关键问题,有机渗透要点”等有效策略,让学生慢慢体悟由减法过渡到除法的演变过程,为后续系列教学除法打好了扎实的基础。
【关键词】序列 同数连减解决问题 除法教学 前置性教学
除法教学是小学计算教学的一块基石,在计算教学中具有举足轻重的作用。在四则运算中,由于生活经验相对缺失,除法含义的理解对学生来说更为抽象,是计算教学的难点所在。同时除法教学又是一个庞大家族,包括了除法的概念教学、计算教学和解决问题教学三大类,现将第一学段整数除法教学进行梳理,具体见下图所示:
这些内容在2001年实验版教材中分布比较零散,缺乏序列性。每个單元每个内容的编排没有形成一条主线,相关知识点逐个独立呈现,各树一帜,直接导致学生出现了多处的经验断层。针对这些问题,2011年课标版教材以“一个数里面有几个几”为主线,进行了重新编排,加强了序列性,明晰了每块内容在整个序列中的任务承载。
新人教版教材一年级下册“同数连减解决问题”的内容,是通过“28个橘子,9个装一袋,可以装满几袋”的问题情境引入,引导学生用圈一圈的直观方法进行探索,进而得出用连减方法图示推算,加深减法含义理解,搭建由减法到除法过渡的桥梁,便于学生今后更好地理解除法的意义,进一步感知去尾法。作为除法前置性教学的内容,本课教学重在承接从画一画、圈一圈到用连减算式表征的纽带,同时也是孕伏减法与除法的联系,并让学生初步感知“进一和去尾”,为后续的除法学习奠定基础。
一、依托课始孕伏,唤醒知识储备
“同数连减解决问题”在“一个数里面有几个几”的序列教学中有着承前启后的作用。在本课设计时,我们必须唤醒学生已有的知识储备,从而更好地沟通图示与算式表征。只有明确学生知识起点,才能更好地唤醒学生的知识储备,我们采用前测问卷的形式来探知学生的学习起点,出示前测题:
由于前面(一下第46页例7教学)知识的迁移,全班只有一种答案,那就是通过画图圈一圈来解决问题。从前测说明,学生已经能熟练地运用图示表征的方式来解决“一个数里面最多有几个几”的问题,但其他的知识储备(用减法解决问题)未曾唤醒,导致解题策略唯一,阻碍了图示表征与算式表征的顺利融合。
为了突破解题策略唯一,更好地唤醒学生的知识储备。笔者预设了两个复习铺垫题,口算接龙和一步计算解决问题。
经过课始的有效孕伏,在例题(有28个橘子,9个装一袋,可以装满几袋?)的探究学习时,学生用自己喜欢的方式来表示装橘子的过程。部分学生采用画一画、圈一圈的方法,部分学生采用28-9-9-9=1的连减算式,有个别学生采用28-9=19 19-9=10 10-9=1,也有个别学生出现了28-9=19-9=10-9=1(错误)。这个环节的设计不仅承接了图示表征解决“一个数里面有几个几”的策略,同时也唤醒了学生运用减法来解决问题的策略,更好地为后续教学做好了铺垫。
二、梳理核心策略,助力模型建构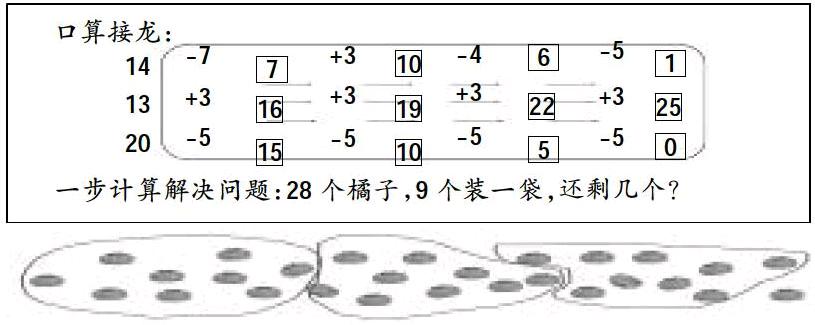
要想更好地建构解题模型,教师就必须将学生呈现的多种策略进行有效沟通,从而让学生掌握解决“一个数里面最多有几个几”问题的关键点,梳理出核心策略,更好地建构解题模型,为后续除法含义的建构做好铺垫。
【教学片段】
出示例题:有28个橘子,9个装一袋,可以装满几袋?
学生独立探索、反馈交流(先图示再算式)。
展示学生作品:
28-9=19 19-9=10 10-9=1
口答:可以装满3袋,还剩1个。
28-9-9-9=1
口答:可以装满3袋,还剩1个。
本环节在实施过程中分三步走:说一说,学生自述思考过程;指一指,沟通图形与算式之间的联系(以教师引着指、学生互动提问指等多种形式展开);比一比,沟通不同算式间的联系。
这里关键在第二步“指一指”。我们不仅要求学生说说算式中每个数字所表示的含义,并要求在图示中指一指。教学中,教师边引导学生用手指,边适时补充“这个9原来就是圈走一袋的9个啊,那么19呢?这个9呢?”在学生边说边指的过程中,让他们完全理解每个算式表示的含义,同时也将算式与图示进行无缝对接。同时通过对比三道算式,让学生明白原来都是减了3个9,就是说28里面最多有3个9,可以装满3袋。
在这个过程中,将半抽象的图示表征与抽象的算式表征进行无缝对接,沟通解决问题多种策略之间的关系,从而建构解题模型。同时以相同个数为一份,通过不断地分、不断地减去相同数的一些操作学习活动,都为学习除法积累最有效的基本活动经验。
三、抓住关键问题,有机渗透要点
本课作为除法教学中最重要的一站,在实施推进过程中需要将除法的要点知识进行有机渗透。
(一)关注“几个几”,渗透除法含义
在整节课的学习中,我们应该时时强调一个数里面有几个几,为学习除法做好铺垫。如在提问“可以装满几袋”时,需要追问“你是怎么知道的”,让学生深刻理解连续减几个9,连续减几个7,就是28里面最多有几个9,28里面最多有几个7,就是可以装满几袋。现摘录部分课堂中的师生对话。
【教学片段】
师:刚才我们用了画一画、圈一圈、算一算的方法解决了这个问题,那么让我们再来回顾一下,你是怎么知道可以装满3袋,还多1个呢?
生:我用圈一圈的方法,9个一圈9个一圈,这样圈了3圈,还多1个,就是可以装满3袋。
生:这道算式从28里面连续减了3个9,那就可以装满3袋,还多1个。
师一边指图一边说:原来是这样,9个一圈,就是1个9,2个9,3个9,28里面最多有3个9,这里的算式从28里面连续减了3个9,还剩1个,都说明28里面最多有3个9。所以可以装满3袋。
……
在上述环节中,由于一年级学生逻辑思维发展的滞后性,引导学生借助图示与算式表征来描述“一个数里面最多有几个几”,降低思维与语言表达的难度,助推学生逻辑思维的发展。为二年级下册系统学习除法含义做好前期的知识储备。在后续的除法初步认识中的含义建构时,学生就能顺利地提取知识储备,学得游刃有余。
(二)感知“最多”,体悟答案唯一性
“一个数里面最多有几个几”,这里的“最多”如何让学生有效的理解,从而更好地为后续学习有余数除法里“余数一定要比除数小”进行有机渗透?这就需要我们在教学中进行有意为之。
【教学片段】
新授环节:“28个橘子,9个装一袋,最多装几袋?”装一袋后,提问:还能装吗?再装满一袋后,提问:现在还能装吗?让学生感知,装到不能够再装满一袋为止。
练习环节:
选一选,穿珠子,22颗珠子,5个一串,最多可以穿几串?
师:想好答案了吗?一起用手势表示出来。为什么大家都选2?
生:因为问题是最多,第一个答案最后还剩下7颗,还可以再穿一串,而第二个答案最后剩下2颗,不能再穿一串了,所以答案是2。
师:那么最多可以穿几串,还多几颗,你是怎么想的,我们一起来数一数。
教师一边圈“-5”,一边齐数“1个5,2个5,3个5,4个5”。
师:22里面最多有4个5,所以最多可以穿4串,还多2颗。
师:做了这一题,你想提醒小朋友们什么呢?
生:我想提醒小朋友们,在做题时,我们要减到不能再减了为止。
师:什么叫不能再减了呢?
生:就是最后剩下的数要比减数小,就是不能再减啦。
……
不管是新授环节的不断追问,还是练习环节的选择,都是有意让学生感知“最多”,目的是引导学生初步感知剩余的数比减数要小,当余下的数比减数大时,说明还可以再穿一串,为以后学习有余数除法,余数一定要比除数小,即答案的唯一性进行前期渗透。促使学生在学习二年级下册有余数除法单元中 “余数与除数关系”时,他们能通过拼组、观察、比较,很自然地唤醒原有的知识储备。即“余下的數要比减数小,减到不能再减了为止(以现有的知识基础)”,也就能顺利地建构“余数要比除数小”的概念。
(三)体验“至少”,孕伏进一法原理
关于“至少”也是用有余数除法解决问题的一种基本形式,我们可以在课堂拓展环节渗透对“至少”的理解,让学生结合生活经验,初步感知“进一法”。
如在课的延伸环节,出示以下习题,引导学生独立思考,然后进行反馈交流。
生:10-4-4=2(只),答:至少需要2个笼子。
生:10-4-4=2(只),答:至少需要3个笼子。
引导学生讨论,为什么算式相同,答案不同呢?
经过学生之间的讨论交流得出结论:如果是2个笼子,那么还有2只兔子没有笼子住,所以还需增加1个笼子。同时学生也恍然大悟,碰到这类问题时,有时我们还要结合生活实际进行思考。
师:那么再多些笼子可以吗?
生:可以是可以,但是太浪费啦。……
师:在解决这类问题时,我们一般要思考,在最节省的情况下,需要几个笼子。也就是最少需要几个笼子。
在这个环节中,通过让学生解决至少需要几个笼子的数学问题,结合生活中的应用经验,让学生初步感知“至少”,为二下学习用有余数除法解决问题中的“进一法”进行有效的铺垫。
“一个数里面有几个几”的教学在2011年课标版教材中推进序列做得较细致,通过前期一步步地渗透与引导,让学生慢慢体悟由减法过渡到除法的演变过程,加深了四则运算间的沟通与联系,而“同数连减解决问题”的教学在整个序列的推进中起到了承上启下的作用,为后续系列教学除法打好了扎实的基础。
(浙江省宁波市奉化区岳林中心小学 315500 浙江省宁波市奉化区新城实验小学 315500)
