认知无线电中一种改进的AVC频谱感知算法

何智勇

（南京工业职业技术学院，江苏 南京 210023）

认知无线电中一种改进的AVC频谱感知算法

何智勇

（南京工业职业技术学院，江苏 南京 210023）

AVC算法是一种适用于拉普拉斯噪声环境的常用频谱感知算法，但该算法并未充分平滑拉普拉斯噪声中的“尖峰”，导致算法的检测性能不佳。针对此，提出一种改进的AVC频谱感知算法，其原理是对接收信号绝对值做开根号处理，并累加处理结果，作为检验统计量，进而判决是否存在主用户，实现频谱感知。此外，利用中心极限定理推导了所提算法检验统计量在主用户不存在时的概率密度曲线，从而给出理论判决门限。仿真表明，所提算法的检测性能分别优于AVC感知算法和拉普拉斯噪声下的能量检测算法大约1 dB和4 dB。

频谱感知；拉普拉斯噪声；中心极限定理；理论判决门限

1 引言

固定的频谱分配政策和无线电的快速发展导致了授权频段的低利用率和非授权频谱的拥堵，在这种情况下，认知无线电（cognitive radio,CR）应运而生，其核心思想是通过频谱感知技术发现“频谱空洞”，在不干扰主用户通信的前提下允许次用户使用空闲频谱。因此研究快速有效的频谱感知算法显得尤为重要[1,2]。

目前，常见的感知算法主要有能量感知算法、基于特征值类感知算法以及基于拟合优度感知算法[2-4]。这些已有的频谱感知算法大部分都是在理想的高斯背景下提出，由于实际无线电接收设备所处的环境存在着大量的无线信号和各种复杂的干扰，导致接收机工作在非高斯背景噪声环境中。如日常生活中的微波炉设备引起的脉冲性噪声[5]，该类噪声含有的较大幅度尖峰脉冲的频率远高于理想的高斯噪声，然而高斯噪声中往往不会出现这些具有较大幅值的采样值，因此用高斯噪声来描述这类背景噪声是不合理的[6,7]。

在非高斯噪声背景下，如果直接使用适用于高斯噪声的频谱感知算法，会降低算法的检测性能[6,7]。因此学者们对非高斯噪声下的频谱感知技术展开了研究并取得一定的成果[7-12]。比如参考文献[9]提出一种适用于一种非高斯噪声（广义高斯噪声）的Rao Test感知算法，该算法不需要知道噪声方差，但需要知道广义高斯噪声的具体参数。参考文献[10]设计了一种适用于拉普拉斯背景噪声的协作感知算法，与高斯背景噪声不同的是，Tan证明了拉普拉斯背景噪声下的OR融合准则不再是硬融合准则下最佳的融合方案。最近，Gao[7,12]对拉普拉斯背景噪声下能量检测（energy detection with Laplacian noise，LED）算法进行了研究，并指出能量检测算法在拉普拉斯背景噪声中检测性能发生了下降。这是由于相比于高斯白噪声，拉普拉斯噪声的概率密度函数（probability density function，PDF）带有明显的拖尾且具有较多的“尖峰”，在相同的判决门限下容易引起较大的虚警概率。若要提高拉普拉斯噪声下的检测性能，必须处理掉拉普拉斯噪声中的“尖峰”值。在通信信号处理中，常用平滑器来处理信号中的“尖峰”值，因此Gao利用开方器对接收信号进行平滑处理，并将接收信号的绝对值之和作为检验统计量，从而给出拉普拉斯噪声下基于绝对值之和的AVC（absolute value cumulating）算法[12]。并且通过仿真证明了AVC算法检测性能优于LED算法大约3 dB。

相比于LED算法，AVC算法在不增加复杂度的同时提高了检测性能，但Gao[12]在绝对值平方的基础上采用开方器平滑拉普拉斯噪声的效果有限。为此在参考文献[12]的基础上，对接收信号绝对值做开方运算，平滑接收信号中的拉普拉斯噪声，并将处理之后结果的累加作为检验统计量，此外，进一步推导了主用户不存在时检验统计量的概率密度函数，给出了判决门限的理论表达式，从而给出一种改进的AVC（modified AVC，MAVC）感知算法。仿真表明，所提算法的检测性能分别优于 AVC和 LED算法1 dB和4 dB。

2 系统模型

2.1 检测模型

频谱感知通常可以描述为如下的二元假设模型：H0表示待检测频段不含主用户信号；H1表示待检测频段含有主用户信号。

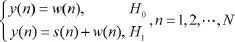
其中，s(n)是次用户接收到主用户所传输的信号；N表示采样点数；w(n)是一个均值为0、功率为2b2的拉普拉斯噪声（在高斯背景噪声下，w(n)是一个均值为0、功率为2b2的高斯噪声），其概率密度如下：

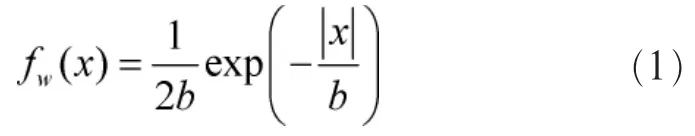
为不失一般性，假设 s(n)和 w(n)相互独立，且满足η=10lg(Ps/2b2)，其中η表示信噪比（signalnoiseratio,SNR），表示主用户发射信号的平均功率。

在实际的通信系统中传输的信号一般可以用复信号表示，但复信号可以表示为实部和虚部，如果分开考虑实部或者虚部，传输信号可以假设为实信号，因此，如无特殊说明，下文表示的信号均为实信号。

2.2 LED算法和AVC算法

现有拉普拉斯噪声下单节点的感知算法很少，最常用的是LED算法和AVC算法。具体地，LED算法和AVC算法的检验统计量分别为：

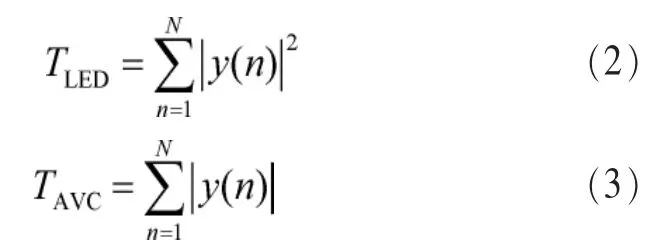
对于上述的两种感知算法，其判决门限可以分别表示为：

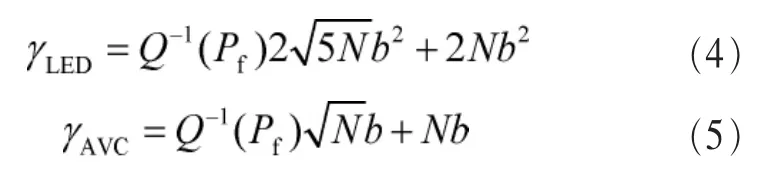
参考文献[7,12]分别给出了LED算法和AVC算法的检测概率表达式，为：

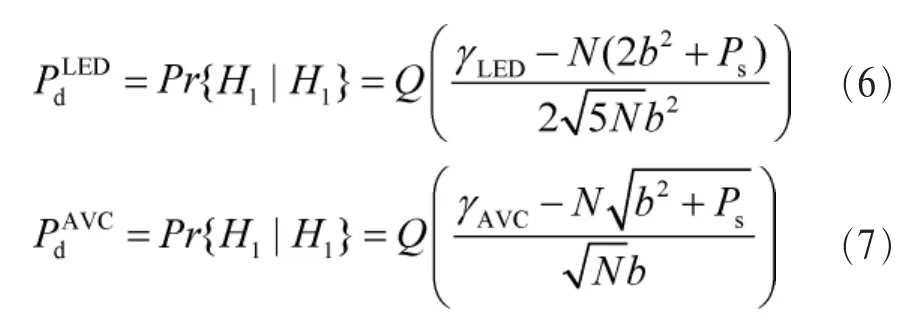
3 所提算法

3.1 算法原理

图1描述了所提算法原理，首先对采样得到的信号取模得到|y(n)|，然后对取模之后的变量进行开方运算（取模和开方运算是为了对接收信号进行平滑处理）并将其累加得到检验统计量T，最后将检验统计量T和预先设定的判决门限进行比较，得到判决结果。因此所提算法的检验统计量和判决准则可以表示为：

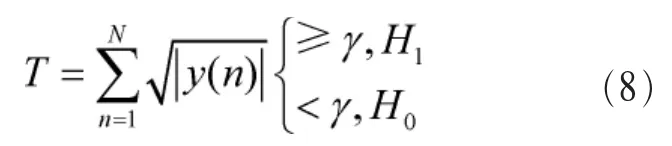
从式（8）可以看出，所提算法的复杂度主要集中于检验统计量T的计算，其复杂度为O(N)。对比式（2）、式（3）可知，所提算法的复杂度和LED算法、AVC算法的复杂度相等。

3.2 理论门限推导

目前，常见的确定判决门限方法有两种[13]：一种是通过蒙特卡洛仿真试验得到判决门限，但当参数（例如采样点数）发生变化且检验统计量不能快速收敛时，判决门限必须通过再次进行蒙特卡洛试验得到；第二种方法是通过推导判决门限的理论表达式，当参数发生变化时，只需计算理论表达式即可得到判决门限。第二种方法具有便捷性、科学性等优点，被广泛运用于频谱感知技术中。本文采用第二种方法来确定所提算法的判决门限，下面利用中心极限定理来推导H0时检验统计量的概率密度函数，并利用纽曼皮尔逊准则来确定判决门限的理论表达式。

在H0时，结合式（1）可知接收信号y(n)服从均值为0、噪声方差为2b2的拉普拉斯分布，其概率密度函数可以表示为：

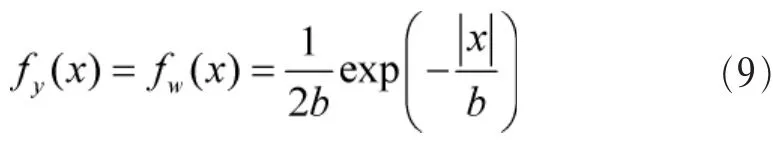
为求解|y(n)|的概率密度函数，给出如下推论。

其中Exponential表示指数分布，b〉0。证明如下。

令z=|x|，易知z有两个单调分支，其反函数分别为：

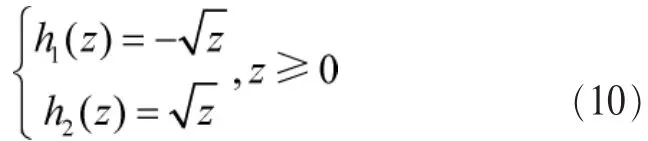
对两个反函数进行求导可得：

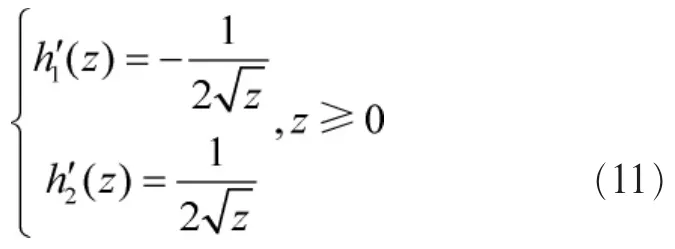
因此|x|的概率密度函数为：

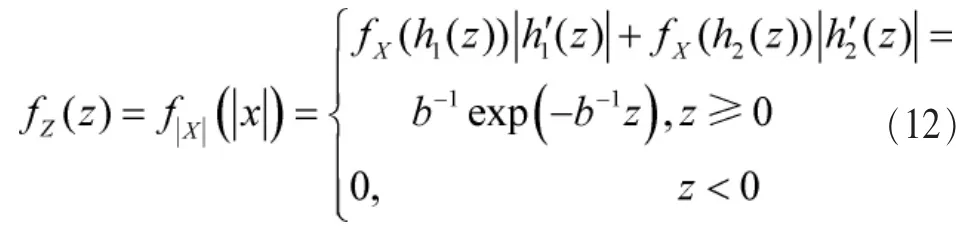
根据推论1可知，|y(n)|服从参数为b-1的指数分布，即，其概率密度函数表示为：

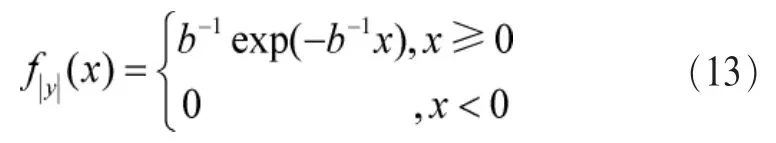
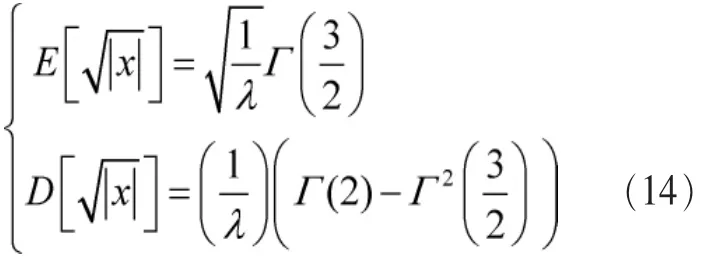
图1 所提算法原理

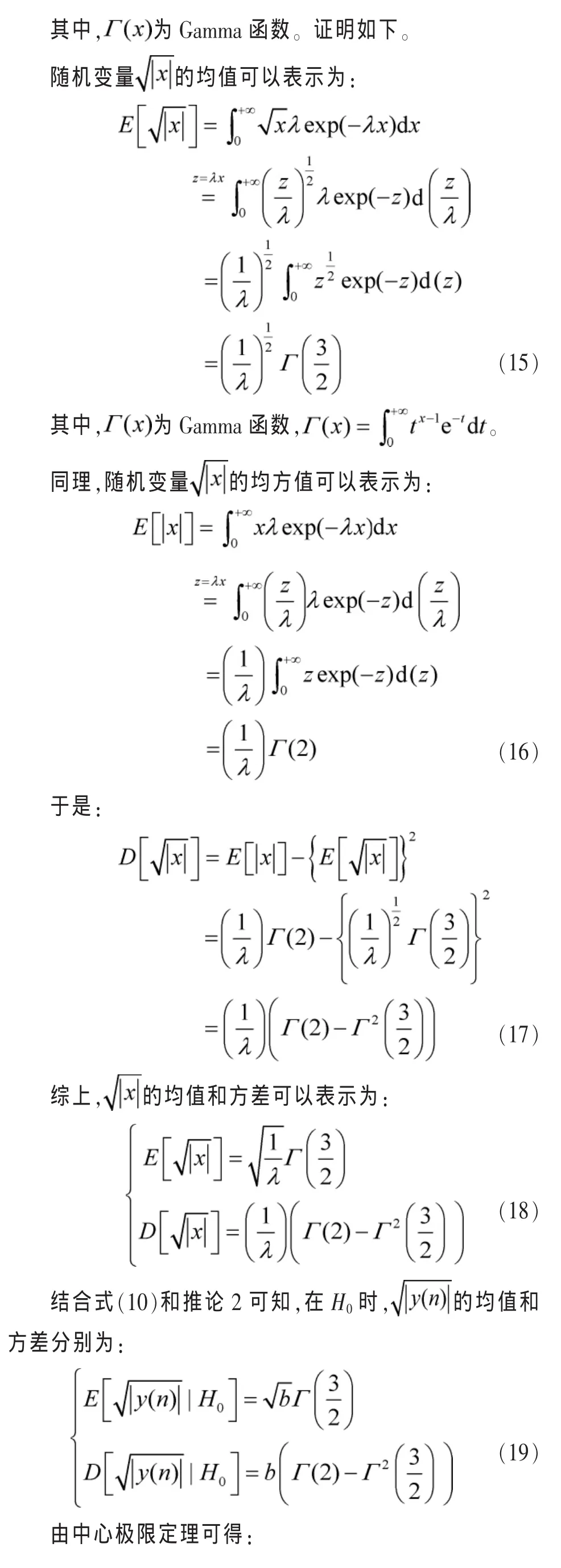
4 仿真分析

对上述的理论进行仿真验证，并通过考察一定虚警概率Pf条件下所提算法所能达到的检测概率Pd来评价其性能，同时与LED算法、AVC算法的性能进行比较。如无特殊说明，仿真中假设拉普拉斯噪声的均值为0、方差为1。

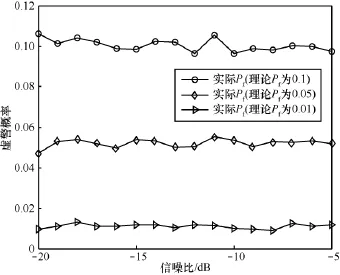
图2 实际虚警概率和理论虚警概率关系

为了验证判决门限的正确性，图2描述了实际虚警概率和理论虚警概率的关系（利用式（24）得到的判决门限代入MATLAB中仿真得到实际虚警概率，理论虚警概率是人为设定）。由图2可知，实际的虚警概率在理论虚警概率附近波动，当理论虚警概率为0.1时，实际虚警概率一般为0.095～0.104，这说明了式（24）所表示的理论判决门限是正确的。

为比较所提算法与LED、AVC算法的检测性能，图3给出了N=300或N=3 000，Pf=0.1时 3种算法的检测性能。由图3可知，所提算法的检测性能明显优于AVC算法、LED算法。比如当N=3 000，信噪比为-15 dB时，所提算法、AVC算法、LED算法的检测概率分别为0.79、0.59、0.38，对于AVC算法，若要达到0.79的检测概率，其信噪比应该在-13.2 dB附近，对于LED算法，若要达到0.79的检测性能，其信噪比应为-11 dB。由此可见，所提算法的检测性能分别优于AVC、LED算法大约1 dB和4 dB。

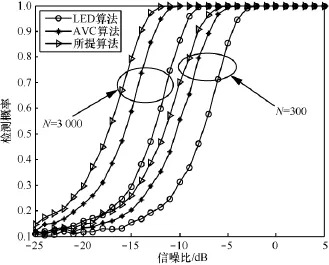
图3 不同信噪比下的检测性能

图4 3种算法的ROC

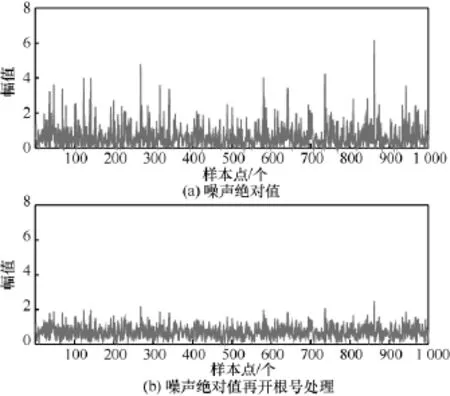
图5 处理之后的噪声样本

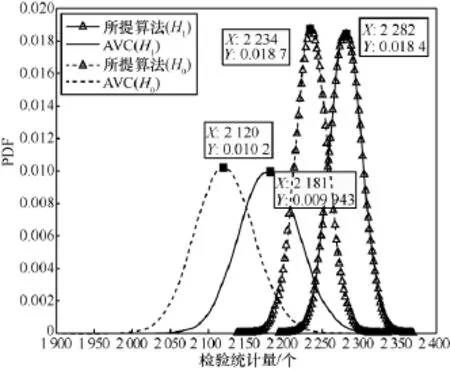
图6 两种算法的PDF

为进一步比较3种算法的检测性能，图4给出了信噪比为-6 dB、N=300时 3种算法的接收器操作特性曲线（receiver operating characteristic curve，ROC）。由图4可知，所提算法的ROC在AVC算法和LED算法的上方，这进一步说明了所提算法的检测性能优于AVC算法和LED算法。

图5给出了拉普拉斯噪声经过不同处理之后的样本点，由图5中可知，拉普拉斯噪声经过绝对值和根号运算之后的尖峰明显少于只经过绝对值运算之后的拉普拉斯噪声。为进一步地比较两种噪声处理之后对检验统计量的影响，图6给出了所提算法和AVC算法在信噪比为-15 dB，N=3 000时两种算法的PDF曲线。需要指出的是，拉普拉斯噪声经过绝对值、根号运算以及累加之后是所提算法的检验统计量，而只经过绝对值运算和累加的是AVC算法的检验统计量。由图6可知，经过根号运算之后的检验统计量在H0和H1的均值差异减小 （如 AVC算法在H1和H0时均值差值为2 181-2 120=61，而所提算法的均值差值为2 282-2 234=48），方差也得到减小（方差反映了数据的波动性，异常点多的数据波动性比异常点少的数据波动性大，因此从两种算法检验统计量的PDF上也可以反映出根号运算在一定程度上减少了“尖峰”），这进一步验证了所提算法优于AVC算法。

5 结束语

本文研究了拉普拉斯噪声下LED算法和AVC算法，并分析了这两种常见算法的不足，针对此，设计了一种适用于拉普拉斯噪声下的MAVC感知算法，其原理是对绝对值做开方处理来滤除拉普拉斯噪声中的“尖峰”，并将其累加之和作为所提算法的检验统计量。此外，利用中心极限定理推导了检验统计量在主用户不存在时的概率密度曲线，进而推导了判决门限的理论表达式。理论分析和仿真表明，在不增加复杂度的前提下，所提算法分别优于AVC算法、LED算法大约1 dB和4 dB。

[1]YE Y H,LU G Y.Blind spectrum sensing based on the ratio of mean square to variance[J].The Journal of China Universities of Posts and Telecommunications,2016,23(1)：42-48.

[2]YUCEK T,ARSLAN H.A survey of spectrum sensing algorithms forcognitive radio applications[J].IEEE Communications Surveys&Tutorials,2015,11(1)：116-130.

[3]PILLAY N,XU H J.Blind eigenvalue-based spectrum sensing for cognitive radio networks[J].Communications IET,2012,6(11)：1388-1396.

[4]WANG H,YANG E H,ZHAO Z,et al.Spectrum sensing in cognitive radio using goodness of fit testing[J].IEEE Transactions on Wireless Communications,2009,8(11)：5427-5430.

[5]TAHER TM,MISURACM J,LOCICERO JL,etal. Microwave oven signal interference mitigation for Wi-Fi communication systems[C]//IEEE Consumer Communications and Networking Conference,Jan 10-12,2008,Las Vegas,Nevada, USA.New Jersey：IEEE Press,2008：67-68.

[6]BEAULIEU N C,YOUNG D J.Designingtime-hopping ultrawide bandwidth receivers for multiuser interference environments[J].Proceedings of the IEEE,2009,97(2)：255-284.

[7]高锐,李赞,吴利平,等.基于随机共振的复杂电磁环境下频谱感知方法及其性能分析[J].高技术通讯,2013,23(8)：811-818. GAOR,LIZ,WULP,etal.Aspectrumsensingmethodviastochastic resonance under complex electromagnetic environments[J]. Chinese High Technology Letters,2013,23(8)：811-818.

[8]LI Q,LI Z,SI J,et al.A novel sequential spectrum sensing method in cognitive radio using suprathreshold stochastic resonance[J].IEEE Transactions on Vehicular Technology,2014, 63(4)：1717-1725.

[9]ZHU X,CHAMPAGNE B,ZHU W P.Rao test based cooperative spectrum sensing for cognitive radios in non-Gaussian noise[J]. Signal Processing,2014,97(7)：183-194.

[10]TAN F,SONG X,LEUNG C,et al.Collaborative spectrum sensing in a cognitive radio system with Laplacian noise[J]. IEEE Communications Letters,2012,16(10)：1691-1694.

[11]MARGOOSIAN A,ABOUEI J,PLATANIOTIS K N.An accurate kernelized energy detection in Gaussian and non-Gaussian/ impulsive noises[J].IEEE Transactions on Signal Processing, 2015,63(21)：5621-5636.

[12]GAO R,LI Z,LI H,et al.Absolute value cumulating based spectrumsensingwithLaplaciannoiseincognitiveradionetworks[J]. Wireless Personal Communications,2015,83(2)：1387-1404.

[13]叶迎晖,卢光跃.基于相关系数的多天线协作频谱盲检测算法[J].电视技术,2016,40(4)：65-68. YE Y H,LU G Y.Cooperative spectrum sensing based on correlation coefficient in multi-antenna cognitive radio[J].Video Engineering,2016,40(4)：65-68.

Modified absolute value cumulating spectrum sensing algorithm in cognitive radio

HE Zhiyong
Nanjing Vocational Institute of Industry Technology,Nanjing 210023,China

Absolute value cumulating (AVC)algorithm is a common spectrum sensing method in Laplacian noise (LED)surroundings,however,the ‘spikes or outliers’in Laplacian noise can’t be fully smoothed,which results in bad detection performance.Aiming at this problem,an modified AVC spectrum sensing algorithm was proposed.The principle was to do the processing of the absolute value of the received signal and the processing result was accumulated as the test statistic to determine whether there was the main user and realize the spectrum sensing.In addition,the central limit theorem was used to deduce the probability density curve of the proposed test statistic in the absence of the primary user,and the theoretical decision threshold was given.Numerical results show that the proposed algorithm outperforms the AVC sensing algorithm and energy detection algorithm with Laplacian noise about 1 dB and 4 dB respectively.

spectrum sensing,Laplacian noise,central limit theorem,theoretical detection threshold

TN92

A

10.11959/j.issn.1000-0801.2017029

2016-07-23；

2017-01-18

江苏风力发电工程技术中心开放基金资助项目（No.ZK16-03-13）；南京工业职业技术学院学校科研基金资助项目(No.YK16-02-01)

Foundation Items：Jiangsu Wind Power Engineering Technology Center Open Fund Project(No.ZK16-03-13),Nanjing Institute of Industrial Technology Research Fund Project(No.YK16-02-01)

何智勇（1984-），男，南京工业职业技术学院讲师，主要研究方向为通信技术、物联网技术。