基于BRT系统总成本最小的站间距优化模型设计

宋 昵 夏贤康

（兰州交通大学交通运输学院，兰州 730070）

基于BRT系统总成本最小的站间距优化模型设计

宋 昵 夏贤康

（兰州交通大学交通运输学院，兰州 730070）

近年来，我国的快速公交建设得到了极大的发展，许多城市都已开通 BRT 系统并逐渐广泛应用，常用的优化模型有以乘客总出行时间最短为目标的站间距优化模型或以社会经济效益最大为目标的站间距优化模型等，此类模型考虑得都较为片面，只从乘客、运营者或政府单个视角考虑站间距的设置，而没有综合加权予以优化。本文基于BRT系统总成本最小的角度来建立数学模型，分别通过分析计算求出各部分的成本，确定BRT的最优站间距，最后以临沂市BRT建设为实例求解最优站间距，验证了模型的可行性。

BRT系统；最小站间距；优化模型

近年来，我国的快速公交建设得到了极大的发展，许多城市都已开通BRT系统并逐渐广泛应用，但同时也出现了一些不可忽视的普遍性问题[1]。通常情况下，合理的站间距会对乘客的出行时间、BRT车辆的运行效率、运营投资者的经济效益、城市的社会效益等很多方面产生有益的推动力，应该通过合理的规划及分析来确定站间距大小[2]。我国一些开通运营BRT系统的城市对于站间距的设定存在一定的主观随意性，没有综合考虑到沿线站点的居民聚集情况、土地利用性质、城市空间布局等因素，因而有必要对站间距进行优化设计。

1 站间距优化模型

BRT系统总成本包括乘客出行成本和系统运营成本两方面，而乘客出行成本由出行时间成本和出行费用成本组成，运营成本由车辆成本和线路成本组成[3]。

1.1 乘客出行总成本

乘客出行总成本由时间成本和费用成本组成[4]，使出行总成本最小得出：

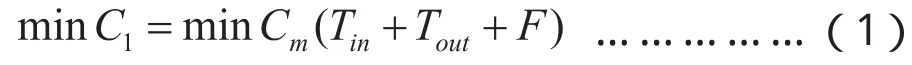
其中C1—乘客出行总成本，Cm—价值系数，Tin—乘客车内时间，Tout—乘客车外时间，F—乘客乘车费用。

（1）乘客车内时间：包括车辆行驶时间T1和车辆停靠站点时消耗的时间T2。

式中：L—某条BRT线路长度（m），Q—某条BRT乘客需求（人/m），Lj—乘客平均乘距（m），v—BRT车辆稳定行驶速度（m/s），m—乘客经过的站点数（个），a—进站制动减速度（m/s2），b—离站启动加速度（m/s2），ts—BRT车辆停站损失时间（s），d—相邻站台之间平均距离（m），所得Tin为：

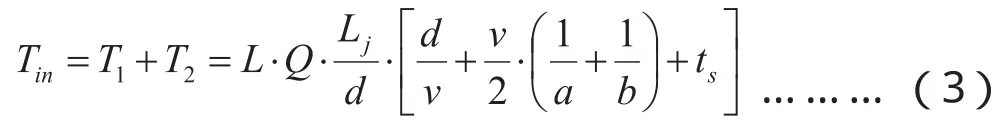
（2）乘客车外时间：分别为步行到站时间Ta、购票及候车时间Tb、离站步行到达目的地时间Tc，对于一条BRT固定的线路，乘客步行到达车站的过程一般为首先步行到达该条公交线路，然后对比前后站点位置离乘客的距离，选择距离最近的站点步行到达，乘客步行到达BRT线路的时间为：

式中：l—乘客步行到BRT线路平均距离（m），va—乘客步行平均速度（m/s）。

乘客到达所乘 BRT 线路后，处于前后两个BRT站点之间，此时需要考虑选择哪一个站点乘车，如图1所示。

图1 乘客站点选择示意图

为保证乘客站点的选择不影响最终站间距大小的确定[5]，应使乘客步行到达K+1站点的时间加上候车时间等同于到达站点K的时间加上车辆行驶至K+1站点的时间与候车时间之和：

式中：E，F—乘客位置离站点距离（m），Td—乘客在站点购票等待时间（s），TR—BRT车辆在两站点之间行驶时间（s），车辆在两站点之间的行驶时间包括稳定车速行驶时间与车辆停靠过程时间：

式中：tsd—BRT车辆停靠延误时间（s）。

结合式5、6可以得出：

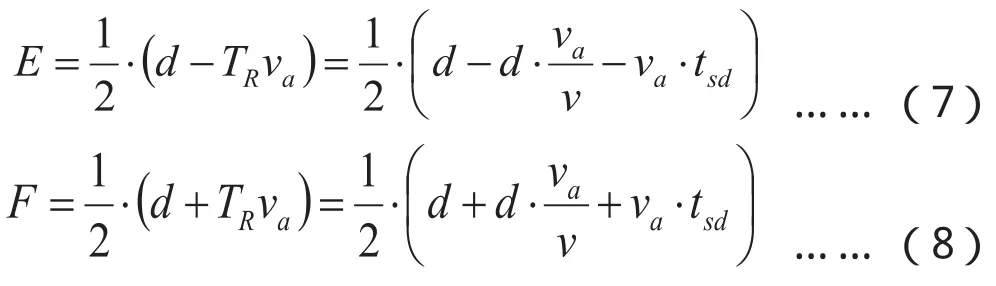
因此乘客沿BRT线路到达最近站点的时间Ta2为：

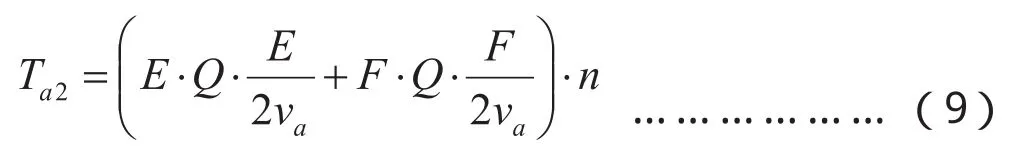
式中：n—BRT线路上的站点数（个）。

所以乘客步行到站时间Ta为：

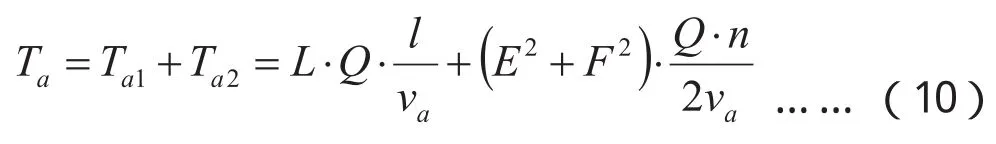
乘客购票及候车时间与BRT车辆发车频率有关[6]。在随机条件下候车时间约为发车频率的二分之一，因此乘客候车时间Tb为：

式中：f—BRT车辆平均发车频率（s）。

乘客离站到达目的地的时间Tc与乘客步行到站时间Ta相同，故Tc=Ta。

因此乘客车外时间Tout为：

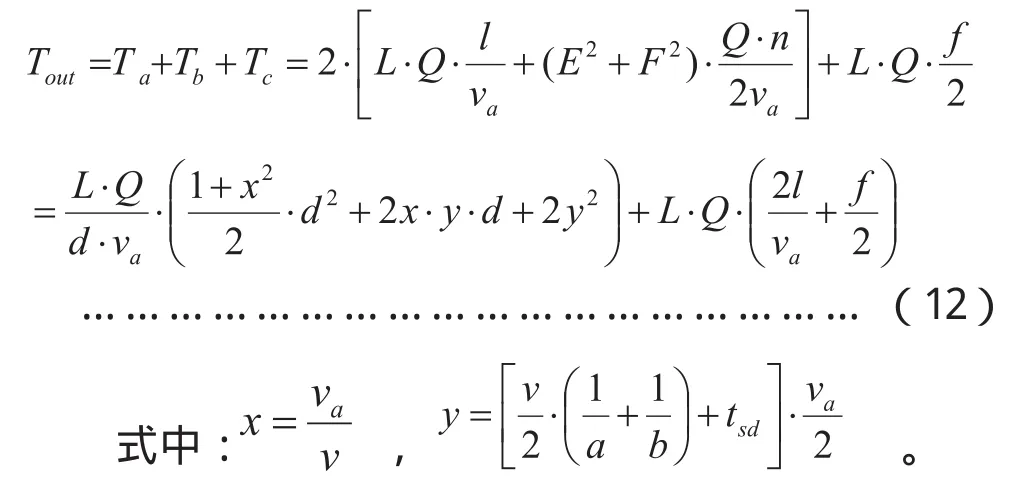
（3）乘客乘车费用：乘客乘车费用F与乘客的乘坐距离有关[7]，为方便计算，本文简化为乘客的平均乘距，则乘车费用：

式中：Fa—单位距离费用。

由以上分析计算可得出乘客出行总成本C1为：

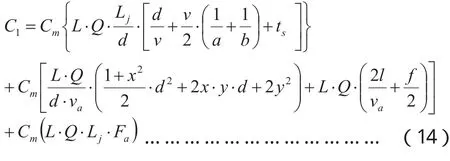
1.2 BRT系统运营成本

BRT系统运营成本C2由车辆成本Ca和线路运行成本Cb组成：

BRT线路所需要的车辆数N1为：

因此车辆成本Ca为：

BRT线路运行成本Cb为：

式中：λa—BRT运行单位里程成本，λb—BRT运行单位时间价值，TD—BRT单向运行时间（s），TN—线路日运行时间（s），λc—单位乘客上下车时间（s）。

因此BRT系统的运营成本为：

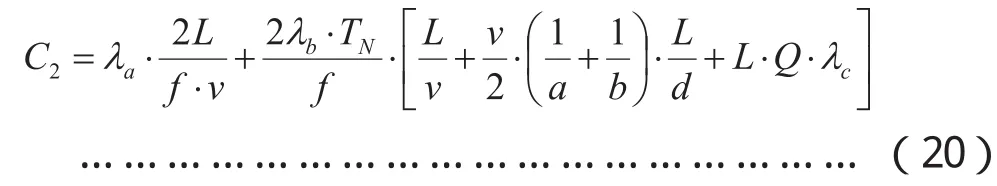
所以得出系统总成本C为：

2 实例应用

2.1 实例概况根据2016年临沂中心城区基础设施及重点项目建设计划，临沂城区首条BRT快速公交工程将开建[8]。沂蒙路BRT工程，线路南起火车站、北至北城换乘中心，全长共计11公里[9]。本文以沂蒙路BRT为例，采用上述站间距优化设计模型来确定该线路的最优平均站间距， 相关的模型参数取值通过实际调查并参照相关规范和国内其他已应用BRT系统城市的建设经验确定[10]。沂蒙路BRT线路走向如图2所示。

图2 沂蒙路BRT线路走向

2.2 求解过程

（1）模型参数设定。上文基于BRT系统总成本最小的站间距优化模型中，为求出最优站间距，式（22）涉及了多个拟定的参数，参照有关规范、其他城市建设经验及临沂市实际情况[11]，各个参数的具体取值见附表。通常情况下，BRT高峰小时客运量约为10000～30000人次，该BRT线路日运行时间15小时， 结合高峰小时客运量及国内其他城市运营情况，我们设定线路日客运量为 10 万人次[12]。

附表 模型参数取值

由附表中相关数据可得，由于车辆停靠产生的延误时间tsd为50s，因此根据公式（6）可知,车辆停站损失时间ts为：

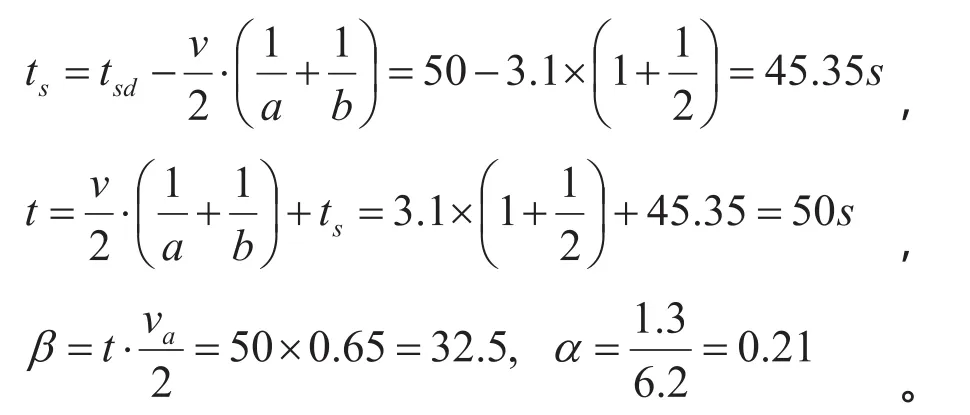
BRT线路所需的车辆数为辆，BRT车辆成本为Ca=0.14×12=1.68。

因此通过基于BRT系统总成本最小的站间距优化模型可得出该BRT线路的最优站间距为721.54m。

3 总结

我国在BRT系统建设方面仍处于初期阶段，应用城市还不够全面普及化，但BRT相关领域的理论研究已经越来越受到重视[11]。本文在借鉴国内外BRT理论研究及部分城市实践经验的基础上[12]，对BRT最优站间距设计方面的问题进行了深入的研究。提出基于BRT系统总成本最小的站间距优化模型，并通过实际案例求出最优平均站间距来验证模型的合理性与科学性，为城市BRT站间距的设定提供了更加客观、可靠、科学的理论支持。

[ 1 ] 唐铮铮.促进城市公交优先，加快城市交通运营[J].城市建设理论研究，2013(17).

[ 2 ] Wilbur Smith and Associates. Under Commission for American Automobile Manufacturers Association [J]. Transportation and Parking for Tomorrow’s Cities[R].1966.

[ 3 ] Gilbert Laporte. Locating Stations on Rapid Transit Lines [J]. Computers& Operations Research，2002.

[ 4 ] 陈建豪. 快速公交系统的研究与发展现状浅析[J]. 城市建设理论研究，2012(14).

[ 5 ] 吕牮楠. 郑州市 BRT 的应用优化研究[J]. 交通与运输，2010(1):82-85.

[ 6 ] 陆锡明，陈必壮. 显著缓解市区乘车难的新设想——封闭式快速公交运营系统的设计[J].上海建设科技，1994，04:17-18.

[ 7 ] 马莹莹，杨晓光，马万经. 快速公交站台形式及位置最佳布置方法[J]. 城市交通，2014(7):50-54.

[ 8 ] 武香林，张永. 城市主干道快速公交（BRT）系统合理站距规划布局[J]. 交通与运输，2012(7):98-101.

[ 9 ] 李春燕，李文权. 快速公交（BRT）线路布局优化研究[J]. 道路交通与安全，2010(5):25-28.

[ 10 ] 王相平，甘军霞，罗楠. BRT 站点布设研究[J]. 交通科技与经济，2013(2):83-85.

[ 11 ] 周再玲，石红文，吴梦，常军乾. 排队论在计算城市快速公交车站停车位数量的应用[J]. 铁路计算机应用，2009(2).

[ 12 ] 胡子祥，赵杰，刘丽亚. 加拿大、巴西发展快速公交的经验及启示[J]. 宏观经济研究，2014(5).

Design of station spacing optimization model based on the minimum total cost of BRT system

( Lanzhou Jiaotong University, College of transportation, Gansu, Lanzhou, 730070)
Song Ni Xia Xiankang

In recent years, China's rapid transit construction has been greatly developed, many cities have opened BRT system and gradually widely used, commonly used optimization model is the optimal model of station spacing, which is the shortest distance between passengers and the maximum of social and economic benefi ts, these models consider are relatively one-sided, only from the passengers, operators or the government of a single perspective consider station spacing settings, and there is no comprehensive weighted be optimization. In this paper, based on the point of view of the total cost of BRT system to establish a mathematical model, respectively, through the analysis and calculation of the cost of each part, determine the optimum station spacing of BRT, Finally, the feasibility of the model is verifi ed by taking the BRT construction of Linyi as an example to solve the optimum station spacing.

BRT system; minimum station spacing; optimization model

U492.4+32

A