基于双轴调整棱镜的惯导缓冲基座方位引出

涂勇强，杨功流，朱景波，万振塬，殷 珂

（1.北京航空航天大学仪器科学与光电工程学院，北京100191；2.北京兴华机械厂，北京100854)

基于双轴调整棱镜的惯导缓冲基座方位引出

涂勇强1，杨功流1，朱景波2，万振塬1，殷 珂1

（1.北京航空航天大学仪器科学与光电工程学院，北京100191；2.北京兴华机械厂，北京100854)

分析并设计了一种将带双轴调整机构的棱镜作为基准棱镜的方位引出方法，并基于此提出了惯导缓冲基座复位精度试验方案。首先，根据直角棱镜作基准棱镜时放置位置对方位引出的影响，设计可双轴调整机构；然后，从双轴调整机构出发，利用坐标变换和矢量形式的棱镜反射公式推导了放置误差造成的方位引出误差，根据误差公式设计了试验方案；最后，分析与估算了方位引出精度，结果表明：此方案在控制经纬仪望远镜的俯仰角小于15°时，方位引出的均方误差小于5″。

缓冲基座；方位引出；双轴调整机构；棱镜；复位精度试验

0 引言

配备于惯性导航系统的并联缓冲器不仅能抵抗大冲击，还具有优于15″的复位精度［1］。在实际使用前，需对惯导缓冲基座进行复位精度的试验验证。试验中，将模拟惯导系统的工装固定在并联缓冲基座动平台上，分别在冲击试验前后测量并记录动平台的水平姿态和方位，将前后的差值作为缓冲基座的复位精度。因此，试验前后的动平台水平姿态和方位的测量是缓冲基座复位精度评定的关键，缓冲基座15″的复位精度要求测量精度达到角秒级。

水平姿态的测量可利用差分工作方式的电子水平仪测量，最高测量精度可达0.2″［2］，能较容易地满足角秒级测量精度。而方位的测量精度较差，目前方位引出的常用方法有应变传感器测量法［3］、GPS测量法［4］、摄影测量法［5］、基准镜光学引出法［6⁃8］等。其中，应变传感器测量法和GPS测量法易受环境影响，摄影测量法测量小型结构误差大；相对而言，基准镜光学引出法受环境影响最小，精度最高，文献［9］将平面镜作为方位基准镜，实现了均方误差不大于3″的方位引出。但实际使用平面镜作方位基准镜时，需调整经纬仪望远镜的出射光线垂直于平面镜平面，存在调整困难、费时的问题。为解决该问题，用直角棱镜代替平面镜作方位基准镜，但直角棱镜的放置会给基准棱镜的方位引出带来误差［10⁃11］，需要对误差进行分析并消除。

本文设计了一种棱镜的双轴调整机构和相应的方位引出方案，并对该方案进行方位引出的精度分析。首先，针对直角棱镜作基准棱镜时放置位置对方位引出的影响，设计可双轴调整机构；然后，在此机构的基础上利用坐标变换和棱镜反射公式推导了放置误差造成的方位引出与水平引出误差，根据误差公式提出相应的调整方案和方位引出试验方案；最后，分析与估算了方位引出精度。

1 双轴调整机构的构造

1．1 双轴调整机构在方位引出中的位置

采用精度较高的基准镜光学引出法测量缓冲基座的方位变化，图1所示为在惯导缓冲基座复位精度试验中应用配备双轴调整机构的直角棱镜作为基准镜的方位引出方案。负载与缓冲基座固联，缓冲基座的方位由通过双轴调整机构固联在负载上的基准棱镜引出。从电子经纬仪望远镜目镜发出的出射光线首先在棱镜的入射面发生折射进入棱镜，再分别在两个相互垂直的反射面发生反射改变光路，最后在棱镜入射面折射出棱镜，返回光线被经纬仪望远镜物镜接收并在CCD上成像。冲击实验前，先使返回光线在物镜上成的十字像的垂直线与垂直刻画线重合作为初始位置；冲击试验后，通过在物镜上的垂直光线与垂直刻画线的角度偏差读取方位的变化，将此作为缓冲基座的复位精度。

图1 方位引出试验Fig．1 Azimuth transfer experiment

1．2 双轴调整机构的组成和调整方式

针对棱镜放置对方位引出的影响，设计双轴调整机构如图2所示，棱镜的双轴调整机构主要由内框架和外框架组成。首先，通过压盖、压盖垫片、侧盖、侧盖垫片及螺纹连接件将直角棱镜固定在内宽架上构成内框架组件；然后，将内框架的销钉插入外框架的销钉孔，通过内框架圆弧槽的内框锁定螺钉将内框架固定在外框架上；最后，同样的方法将外框架固定在工装上。图3所示为转动轴的实现方法，内框架的销钉、圆弧槽及锁定螺钉调整了棱脊相对于棱镜垂直轴的转动；外框架的销钉、圆弧槽及锁定螺钉调整了棱脊相对于水平面的转动。通过内框和外框2个轴的转动可以消除棱镜放置对方位引出的影响。

图2 棱镜的双轴调整机构爆炸图Fig．2 Explosive view of prism's two⁃axis adjustment mechanism

图3 棱镜的双轴调整机构三视图Fig．3 Orthographic views of prism's two⁃axis adjustment mechanism

2 棱镜放置对方位引出的影响

根据双轴调整机构推导棱镜放置对方位引出的影响。如图4所示，A系为瞄准坐标系，满足：OA⁃XAYA面为水平面，经纬仪出射光线L1在OA⁃XAZA内，OA⁃XAYAZA构成右手系；P系为棱镜坐标系，满足：OP与OA重合，OPYP与棱脊重合，OPXP垂直于棱镜入射面向外，OP⁃XPYPZP构成右手系。同时，A1和A2分别是棱镜的反射面，视棱镜为理想棱镜，可不用考虑光线在棱镜入射面的折射，L1和L2即为不考虑折射的棱镜入射和出射光线。

图4 A系和P系中任意位置的棱镜光路图Fig．4 Bean path diagram of prism in A⁃frame and P⁃frame

令ψ、θ、φ分别为棱镜棱脊依次相对OAZA、OAYA、OAXA的放置偏转角，则瞄准坐标系OA⁃XAYAZA到棱镜坐标系OP⁃XPYPZP的转换矩阵为：

得到棱镜坐标系OP⁃XPYPZP到瞄准坐标OA⁃XAYAZA的转换矩阵：

在棱镜坐标系内，反射面A1和A2的法线的单位向量分别为：

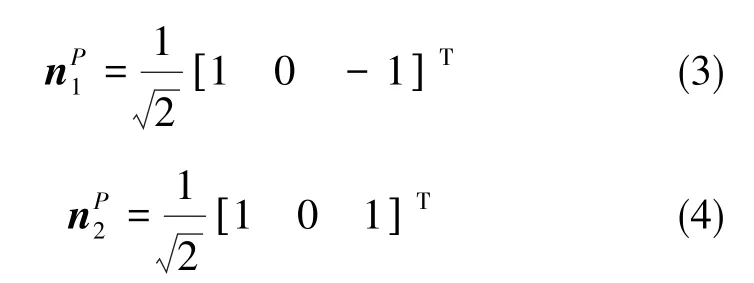
通过P系到A系的坐标转换，反射面A1和A2的法线的单位向量在瞄准坐标系下分别为：

设经纬仪望远镜的出射光线的俯仰角为ε，棱镜的入射光线单位向量L1为经纬仪望远镜的出射光线：

由矢量形式的反射定理［12］，L1经过第一个反射面反射得到L1′，L1′经过第二个反射面反射得到L2：

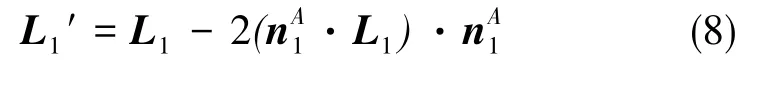
利用矢量乘积公式，将式（8)、式（9)推导成式（10)：

双轴调整机构可以通过绕销钉旋转内框架和外框架调整ψ和φ，θ由外框架与内框架的配合精度和外框架与工装的配合精度决定，将θ视为小量，由式（5)～式（7)、式（10)得到出射光线矢量：

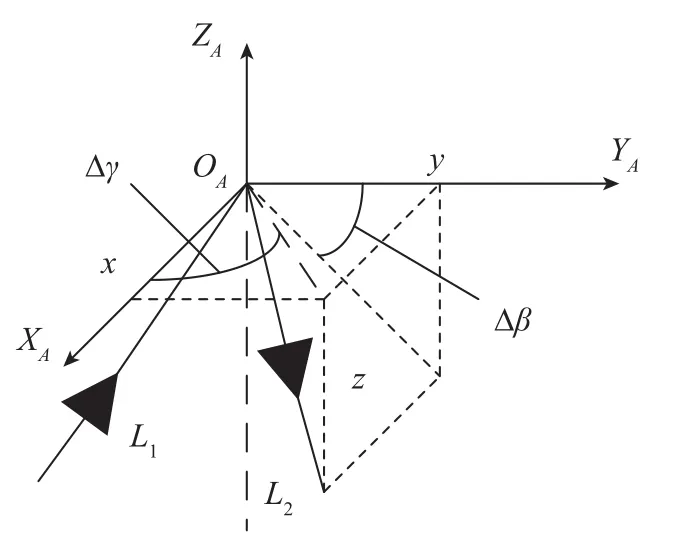
图5 出射光线与入射光线在瞄准坐标系下的方位与水平误差Fig．5 Error of azimuth transfer in A⁃frame

根据图5所示的几何关系，方位引出的方位误差公式为：

方位引出的水平误差公式为：

由式（11)～式（13)可以得到，未进行调整时通过棱镜双轴调整机构固联的棱镜进行方位引出的方位误差和水平误差公式分别为：

由自准直原理，方位角偏差是方位误差的1／2，即：

3 双轴调整机构调整和方位引出试验方案

根据式（14)、式（15)设计棱镜双轴调整机构的调整和方位引出试验的实验方案步骤。

1)入射光线调水平。如图6所示，在图1的基础上，通过缓冲基座动平台上的水平仪调节缓冲杆的限位螺母，使动平台成为水平面；调节经纬仪支架的高度让望远镜俯仰角为0且出射光线能进入棱镜；在动平台上放上标准铁，出射光线L1经过标准铁反射面反射的L2回到物镜；调整望远镜的俯仰和方位，使返回的十字光线与十字刻画线重合，此时，ε＝0，L1＝［-100］T。

图6 入射光线水平调整Fig．6 Horizontal adjustment of incident ray

2)棱脊调水平。拿走标准铁和水平仪，调整外框架旋转轴改变φ，当物镜中的水平光线与水平刻画线重合时满足tanΔβ＝0且ε＝0，根据式（15)，得到φ＝0，棱脊在水平面内。

3)棱脊调方位。调整外框架旋转轴，改变ψ物镜中的垂直光线与水平刻画线，重合时满足tanΔγ＝0、φ＝0且ε＝0，根据式（14)，得到ψ＝0，棱镜坐标系P系与瞄准坐标系A系重合。

4 双轴调整机构方位引出精度分析

冲击实验过后，由于动平台的姿态发生改变，φ、θ、ψ将不等于0。其中，ψ的变化是需要引出的方位变化，不属于误差源。θ、φ影响了方位偏差角，属于误差源，且θ的变化可以等效为望远镜的俯仰角ε的变化。因此，ε和φ决定了方位引出的精度，根据缓冲基座的设计φ≤15″，在冲击完试验结束后允许改变望远镜的俯仰角使ε达到度级别，根据式（14)、式（16)得到方位引出精度Δ，计算结果如表1所示。

表1 方位引出的精度Table 1 Accuracy of azimuth transfer

当控制经纬仪望远镜的俯仰角小于15°时，Δ≤4.02″；同时，经纬仪误差μ≤1″，棱镜2个反射面误差ν≤1″，方位引出的均方误差为：

方位引出的均方误差小于5″，满足要求。

5 结论

本文针对惯导缓冲基座的复位精度试验角秒级的测量需求，设计了棱镜的双轴调整机构用于方位引出，利用棱镜放置位置对方位引出的影响设计相应的双轴调整机构调整方案和复位精度试验方案，根据方位引出误差公式得到方位引出精度结果：控制经纬仪望远镜的俯仰角小于15°时，方位引出的均方误差小于5″。该双轴调整机构和试验方案为惯导缓冲基础的复位精度试验提供了有效的技术手段。

［1］王旭，张嵘.惯性平台并联缓冲器复位精度的分析与综合［J］.中国惯性技术学报，2013，21（4)：452⁃455. WANG Xu，ZHANG Rong.Restoration accuracy analysis and synthesis of parallel bumper for inertial platform［J］. Journal of Chinese Inertial Technology，2013，21（4)：452⁃455.

［2］夏桂锁，廖城，伏燕军.平行双关节坐标测量机的标定及不确定度评价［J］.光学精密工程，2014，22（5)：1227⁃1234. XIA Gui⁃suo，LIAO Cheng，FU Yan⁃jun.Calibration and uncertainty evaluation of double parallel⁃joint coordinate measuring machine［J］.Optics and Precision Engineering，2014，22（5)：1227⁃1234.

［3］Baldwin C，Miemczuk J，Kiddy J，et al.Structural testing of navy vessels using Bragg gratings and a prototype digital spatial wavelength domain multiplexing system［J］.Naval Engineers Journal，2002，114（1)：63⁃70.

［4］邱斌，朱建军，贺跃光.GPS在大地及工程变形观测中的应用［J］.矿冶工程，2002，22（2)：16⁃19. QIU Bin，ZHU Jian⁃jun，HE Yue⁃guang.Application of GPS in crustal and engineering deformation monitoring［J］.Mining and Metallurgical Engineering，2002，22（2)：16⁃19.

［5］Conley E，Morgan C K.Speckle photography applied to measure deformations of very large structures［C］.Pro⁃ceedings of SPIE，1995，2446：161⁃168.

［6］Johnson G，Waid J，Primm M，et al.Ship attitude accu⁃racy tradestudyforaircraftapproachandlanding operations［C］.IEEE Position，Location and Navigation Symposium，2012：783⁃790.

［7］Zhang L，Wang A G.Vessel surface equipment attitude measurement based on conventional inertial reference system［J］.Advanced Material Research，2012，629：878⁃883.

［8］Wang A G，Li H，Wang Y，et al.A principle of astro⁃nomical three⁃dimensional position fixing based on single baseline radio interferometry［J］.Chinese Journal of Elec⁃tronics，2011，20（1)：183⁃186.

［9］仲岩，王丹丹，王兴全，等.一种高精度捷联惯组方位引出方法［J］.中国惯性技术学报，2014，22（6)：845⁃848.

ZHONG Yan，WANG Dan⁃dan，WANG Xing⁃quan，et al. Azimuth extraction method for high⁃precision strapdown IMU［J］.Journal of Chinese Inertial Technology，2014，22（6)：845⁃848.

［10］张俊杰，李政阳.直角棱镜用作自准直反光镜的光学特性［J］.宇航计测技术，2009，29（4)：1⁃3. ZHANG Jun⁃jie，LI Zheng⁃yang.The optical characteris⁃ tics of right angle prisms as auto⁃collimating mirror［J］. Journal ofAstronautic Metrology and Measurement，2009，29（4)：1⁃3.

［11］李庆辉，陈良益，高立民.箭上直角棱镜误差对方位瞄准精度的影响［J］.中国空间科学技术，1998，2（1)：61⁃65. LI Qing⁃hui，CHEN Liang⁃yi，GAO Li⁃min.Influence of rocket's right⁃angled prism error on azimuth laying accu⁃racy［J］.Chinese Space Science and Technology，1998，2（1)：61⁃65.

［12］刘万里，欧阳健飞，曲兴华.激光光束入射角度变化对角锥棱镜测量精度的影响［J］.光学精密工程，2009，17（2)：286⁃291. LIU Wan⁃li，OUYANG Jian⁃fei，QU Xing⁃hua.Effect of incident laser beam angle varying on cube corner retro⁃reflector measurement accuracy［J］.Optics and Precision Engineering，2009，17（2)：286⁃291.

Azimuth Transfer of INS's Bumper Based on Prism's Two⁃axis Adjustment Mechanism

TU Yong⁃qiang1，YANG Gong⁃liu1，ZHU Jing⁃bo2，WAN Zhen⁃yuan1，YIN Ke1
（1.School of Instrumentation Science and Opto⁃electronics Engineering，Beihang University，Beijing 100191; 2.Beijing Xinghua Machinery Factory，Beijing 100854)

An azimuth transfer method with prism's two⁃axis adjustment mechanism was analyzed and designed，and the test plan for INS's bumper restoration accuracy experiment was proposed.First，according to the influence to azimuth transfer for prism's placement，a prism's two⁃axis adjustment mechanism was designed.Then，based on the mechanism，er⁃ror formula of azimuth transfer was derived with coordinate transformation and reflection equation in vector form，and the ex⁃periment scheme was presented.Finally，the accuracy of azimuth transfer was analyzed and estimated，and the results indi⁃cate that if the pitch angle of theodolite is no more than 15°，the mean⁃squared error of azimuth transfer can be less than 5″.

bumper;azimuth transfer;two⁃axis adjustment mechanism;prism;restoration accuracy experiment

U666.1

A

1674⁃5558（2017)03⁃01248

10.3969／j.issn.1674⁃5558.2017.01.012

涂勇强，男，硕士，研究方向为惯性导航、惯导用缓冲基座。

2016⁃03⁃08