含引力辅助的小推力多任务探测轨道设计

林浩申，何 兵，赵 欣，刘 刚，安喜彬

(第二炮兵工程大学 空间工程系,西安 710025)

含引力辅助的小推力多任务探测轨道设计

林浩申，何 兵，赵 欣，刘 刚，安喜彬

(第二炮兵工程大学 空间工程系,西安 710025)

针对深空探测时间长、成本高的特点，文中以多任务深空探测为背景，建立了包含多模型、多约束、多变量、多阶段的探测轨道设计模型。通过融合推力工作模式、分段设计目标函数等策略，克服了模型的内点约束限制，降低了优化模型的复杂度。为了提高优化速度、提升优化精度，结合梯度搜索和粒子群算法的特点，研究提出了一种梯度混合粒子群(GHPSO)算法。将该算法应用到多任务星探测轨道设计模型上，得到了发动机的工作时序，并横向对比了该文算法与传统粒子群算法(PSO)和遗传算法(GA)的优化性能。仿真结果表明，文中提出的算法搜索速度快，第1设计阶段GHPSO相对GA提高61.96%，相对PSO提高47.85%，第2设计阶段GHPSO相对GA提高61.87%，相对PSO提高43.66%；精度最高，第1设计阶段GHPSO相对GA平均精度提高了2.86%，最高精度提高了1.24%，相对PSO平均精度提高了4.19%，最高精度提高了3.97%，第2设计阶段GHPSO相对GA平均精度提高了3.33%，最高精度提高了1.63%，相对PSO平均精度提高了4.72%，最高精度提高了3.02%，适用于轨道优化设计类的非线性、多约束全局优化问题。

梯度混合粒子群算法；多任务星际探测；引力辅助

0 引言

自1959年前苏联发射第一颗月球探测器以来[1]，人类迈开了深空探测的步伐，并随着空间科学技术的发展不断向更远、更深的宇宙进发。1977年，美国宇航局开始酝酿一个旨在研究外太阳系的“大旅行”计划， “旅行者一号”借助176年一遇的行星连线的契机，途经木星、土星历经33年飞出太阳系[2]。针对深空探测时间长、成本高的特点，设计更快更高效、更远更经济的深空探测轨道是人类探索深空的必然趋势。

目前的研究主要从三方面提高深空探测飞行任务的效率[3]：一是采用小推力技术提高推进系统的效率[4]；二是利用行星引力场的引力辅助技术[5]和利用天体平衡点的不变流形低能转移技术[6]；三是多目标多任务探测[7]，是追求低成本、高效率的有效途径。

小推力转移轨道优化设计可归结为非线性常微分方程组的两点边值问题。求解该类问题的主要方法包括间接法、直接法、混合法[8]等。间接法实质上通过增加函数乘子和数值乘子作为待求量，把状态微分方程约束和内点约束引入到广义指标中，再进一步求解，该方法的优点是待求量少，解的精度高，但其收敛域窄、对初值敏感的特点增加了该算法的操作难度[8]；直接法操作简单，容易得到可行解，但难以保证解的最优性[9]；混合法结合了前述两种方法的优点，但还需要推导一阶必要条件和事先假定控制策略[8]。

19世纪，Leverrier和Tisserand在天体轨道摄动方面的研究工作是借力飞行技术的源头[10]，利用该技术探测器可在不消耗燃料的前提下获得速度增量。借力飞行轨道设计的本质是全局优化问题，通常采用随机优化方法求解，如遗传算法(Genetic Algorithm)、进化算法(Evolutionary Algorithm)和模拟退火算法等(Simulated Annealing)。文献[11]首次将遗传算法应用在行星探测轨道优化设计问题中。研究结果表明，遗传算法求解精度较高，但收敛速度较慢。粒子群算法作为智能优化算法的一种，因其参数设置少、收敛速度快等优点，在轨迹优化领域的应用日益受到关注[12]，文献[13]研究了基于改进粒子群算法的航天器燃料最省的多脉冲交汇问题，该算法收敛速度较快，但求解精度较低。

本文将梯度搜索的思想融入粒子群算法之中，利用梯度搜索的高效性和粒子群搜索的随机性解决粒子群算法易“早熟”及收敛精度低等问题，提出了一种改进的混合粒子群算法，并将该算法应用在含引力辅助的小推力轨道设计上。

1 基础力学模型

1.1 探测器的动力学模型

探测器的推进方式可分为脉冲推进方式和小推力推进。脉冲推进方式可视为探测器在推力作用时刻获得瞬时脉冲，使得探测器进行Lambert转移，此种推进方式需要优化的参数少，通过解算Lambert轨道可控制探测器在指定时刻转移至指定位置；小推力推进方式需要优化的参数多，通过其微分模型可积分得到探测器的实时状态。文献[14]给出了脉冲推力模型、小推力模型和Lambert转移模型的详细形式，固定时间双脉冲转移示意图如图1所示。

1.2 引力辅助模型

行星引力辅助是指在探测器飞行过程中，利用行星引力场改变自身速度的过程[5]，探测器从无穷远处以相对速度v∞在tGA时刻进入借力天体P的影响球，引力辅助过程示意图[15]如图2所示。

(1)

探测器相对行星的速度大小：

(2)

(3)

式中Rplanet为行星的飞越半径，取值应不小于借力行星半径；uplanet为借力行星的引力常数。

进行行星引力辅助时，探测器的位置还应该满足如下约束条件：

(4)

式中rsc、rplanet分别为航天探测器和借力行星在日心固联坐标系(HEIRF)中的位置矢量；Rp为行星影响球的半径。

利用行星引力辅助后，探测器在不消耗任何燃料的情况下获得的脉冲速度为

(5)

2 多任务深空探测轨道优化模型

2.1 约束条件

深空轨道设计优化的约束条件主要包括发射窗口约束、初始状态约束、终点状态约束、微分方程组约束和行星引力辅助约束等。

(1)发射窗口约束

行星在HEIRF内的空间位置是不断变化的，因此发射窗口的选择对于轨道优化尤为重要，航天任务规划通常是在一个相对较长的时间段内，从地球出发时刻t0应满足如下约束：

(6)

式中 MJDmin、MJDmax分别表示发射任务时间选取的最小值和最大值(改进儒略日)。

(2)探测器初始状态约束

在从地球出发的时刻( t0)，运载火箭能为探测器提供一个最大逃逸速度vΔmax和最大逃逸高程hΔmax，因此t0时刻的探测器位置、速度矢量应该满足如下约束：

(7)

式中m0为探测器初始质量；mmax为探测器的最大运载质量。

(3)探测器终点状态约束

根据不同的空间探测任务，终点约束不尽相同，以设计逃离太阳系的空间轨道为例，探测器在终点时刻tend的状态应该满足：

(8)

即探测器与太阳的相对距离不小于40个天文单位，相对太阳的轨道偏心率不小于1，以保证探测器能完全脱离太阳的引力束缚，在无动力的情形下飞出太阳系；质量变化量不大于携带的燃料质量mfuel。

(4)探测器的运动微分方程约束

探测器在化学推进方式、小推力推进方式及无动力这3种情形下运动方程由文献[14]已经详细给出。

(5)行星引力辅助约束

在轨道设计过程中若选择利用行星引力辅助，引力辅助应该满足式(1)～式(5)。

2.2 优化变量的设计

优化变量的设计和优化模型的构造紧密相关，以欧空局Izzo的MGA-1DSM模型[16]为例，该模型描述了探测器在2个行星轨道间的转移过程，示意图如图4所示。图中，ΔvDSM为探测器进行Lambert转移时需要的速度增量；探测器借助行星引力辅助时获得的速度增量为ΔvGA；T0、T1分别为此次转移的开始时刻和结束时刻；η1为此次转移过程中Kepler段时间占该次转移总时间的百分比。

整个转移过程分为Kepler和Lambert两段，Kepler段探测器采用小推力沿着速度方向以最大推力持续工作；Lambert段探测器采用脉冲转移。

深空探测轨道实质上是若干个上述轨道的拼接，因此可设计优化变量为

(9)

式中t0、m0分别表示发射时刻和初始质量；rsc(t0)、αr、βr描述了探测器的初始位置矢量rsc(t0)=r(t0)[cos(βr)cos(αr)，cos(βr)sin(αr)，sin(βr)]；而vsc(t0)、αv、βv则描述了探测器的初始速度矢量vsc(t0)=v(t0)[cos(βv)cos(αv)，cos(βv)sin(αv)，sin(βv)]；探测器第i次行星引力辅助时获得的速度增量ΔvGAi由δi、γi确定；ΔTi=Ti-Ti-1表示第i次转移耗费的总时间，ηi表示第i次转移过程中Kepler段占该次转移总时间的百分比。

2.3 优化变量的设计

本文研究的是小推力多任务行星探测高速轨道优化设计问题，整体设计轨道时需要优化的变量多，直接得到满足所有内点约束的全局最优解难度较大，因此合理的设计目标函数至关重要，本文对目标函数的设计主要包括以下几步：

(1)混合推力模式轨道设计

直接对小推力轨道进行优化设计的难点在于无法瞄准目标大行星，难以满足引力辅助的内点约束，因此假设探测器能采用化学推进和连续小推力的混合推进方式，以上述MGA-1DSM模型为基础，探测器通过Lambert转移能准确抵达目标行星，优化设计过程中无须考虑引力辅助约束。将目标函数设计如下：

(10)

式中 ΔTi=Ti-Ti-1为第i次转移耗费的总时间；Δt1为探测器最后一次行星借力后发动机工作的时间；Δt2为探测器燃料耗尽后滑行的时间；ΔvDSMi为第i次转移过程中Lambert转移需要的速度增量。

式中加入eΔvDSMi项，能引导ΔvDSMi不断减小，使得各次Lambert脉冲转移趋于0。通过该目标函数能对发射窗口、探测器初始状态以及引力辅助策略进行优化，得到一组满足各项约束的优化结果。

(2)小推力轨道设计

去掉模型中的Lambert转移轨道的同时引入了新的问题：无法瞄准下一颗借力的大行星。为此重新设计指标函数，新的指标函数设计为

(11)

式中di为Ti时刻探测器与目标行星之间的距离。

通过此指标函数引导探测器在无Lambert转移轨道的情形下瞄准行星，进而在满足引力辅助约束的前提下使用引力辅助。

3 梯度混合粒子群算法

3.1 算法思想

传统粒子群算法通过粒子跟踪个体最优解和全局最优解更新粒子的位置矢量和速度矢量，这种搜索思想使得粒子群算法的全局搜索能力较弱，同时也决定了该算法容易陷入局部最优出现“早熟”现象。本文结合梯度搜索的思想，对传统粒子群的搜索方式进行改变，利用相邻代群的全局最优值得到搜索梯度，通过该梯度指引粒子群更新位置和速度矢量，提高粒子群算法的全局搜索能力。

3.2 算法流程

(1)种群初始化

随机初始化第1代群体与第2代群体各粒子的位置向量和速度向量，计算各粒子的适应度函数值，同时记录前两代群体中的最优个体及全局最优个体。

(2)适应度评价

(3)梯度搜索更新

其中，α为一正常数，α越大，算法全局搜索能力越强，α越小，算法局部搜索能力越强。α的取值策略为

(12)

(4)生成新一代种群

(13)

(5)终止条件判定

判断优化结果是否达到给定精度或迭代次数是否达到给定值。若满足给定条件，则终止迭代，并输出最优解，否则转(2)。

该算法的优化流程如图5所示。

4 仿真计算与结果分析

算例问题描述：探测器将于2025年1月1日(儒略日表示为54 000 MJD)至2055年12月31日之间的任意时刻从地球出发，出发时满足式(12)的初始状态约束，其中最大逃逸速度vΔmax=3 km/s，最大逃逸高程hΔmax=1 000 km且方向任意。探测器需要完成的任务包括：(1)利用火星的引力辅助效应，同时对火星进行观察；(2)利用木星的引力辅助效应，同时投放木星探测器；(3)逃离太阳系，进行深空探测。

假设探测器在飞行过程中仅受太阳引力(引力辅助时刻除外)并可在任意时刻在满足引力辅助约束的前提下利用大行星的引力辅助效应，设计一条能完成上述多任务的探测轨道。

假设设备最大载重为1 800 kg，深空探测设备自重500 kg，携带的木星探测设备自重200 kg，携带燃料的质量可根据任务自由调整，燃料罐的质量为所携带燃料的5 %。

探测器的推进系统采用有限推力的电推进，其比冲为3 000 s，推力最大值为0.5 N，推力的大小和方向均可优化。

(1)参数设置

基于本文提出的混合粒子群算法对多任务深空探测轨道进行优化。问题求解分为混合推力模式轨道设计和小推力轨道设计2个阶段。

第1阶段，设置粒子群大小为200，最大迭代次数为2 500，惯性权重最大值为0.9，最小值为0.4，学习因子c1的初始值为2.5，终止值为0.5，学习因子c2的初始值为0.5，终止值为2.5，α的初始值为2.5，终止值为0.5。

第2阶段以第1阶段的结果为初解，假设发动机采取bang-bang控制策略，即推力大小只能为0或最大值0.5 N，方向沿着速度方向或速度反方向。由于具有良好初解，所以设置粒子群大小为20，最大迭代次数为25，其他参数设置不变。

(2)结果分析

给定设计变量的取值范围，仿真计算50次，得到设计变量优化结果的最优值，如表1所示。

表 1 设计变量优化结果

第2阶段混合粒子群算法适应度收敛曲线如图6所示。

小推力多任务行星探测高速轨道在日心坐标系下的示意图如图7所示。图中圆形轨道由内而外分别为地球轨道、火星轨道和木星轨道，“*”代表探测器从地球离开时地球的空间位置，“▯”代表探测器抵达火星借助引力辅助并对火星进行观测时火星的空间位置，“Δ”代表探测器抵达木星借助引力辅助并抛下木星探测器时木星的空间位置；探测器的轨道中细实线代表小推力沿着速度方向持续工作，粗实线代表探测器发动机不工作。

探测器在木星完成引力辅助后开始逃离太阳系的深空探测任务，轨道示意图见图8。图中圆轨道为木星轨道，探测器的轨道中细实线代表小推力沿着速度方向持续工作，粗实线代表探测器发动机不工作。

经过优化后，得到发动机的工作时序，发动机的工作状态与探测器所处的状态如表2所示。

表 2 发动机工作时序

(3)算法对比分析

问题求解分为混合推力模式轨道设计和小推力轨道设计两个阶段，为横向比较算法的性能，分别采用文献[18]所述遗传算法和文献[19]所述粒子群算法进行小推力轨道优化。

针对混合推力模式轨道设计阶段，设置遗传算法种群大小取200，代数设为2 500；粒子群算法种群大小取200，最大迭代次数取2 500。

仿真进行20次，对各种算法的平均精度和最高精度对比见表3。

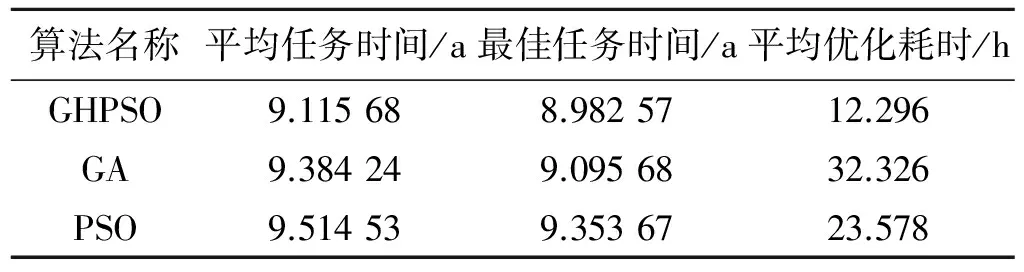
表 3 优化性能对比

仿真结果表明，在求解星际探测轨道时，遗传算法收敛精度较高，粒子群算法搜索速度较快，梯度混合粒子群算法收敛速度最快，GHPSO相对GA提高61.96%，相对PSO提高47.85% ；梯度混合粒子群算法精度最高，GHPSO相对GA平均精度提高了2.86%，最高精度提高了1.24%，相对PSO平均精度提高了4.19%，最高精度提高了3.97%。

针对小推力轨道设计阶段，以GHPSO算法得到混合推力模式轨道设计的结果为初解，设置遗传算法种群大小取20，代数设为25；粒子群算法种群大小取20，最大迭代次数取25。

仿真进行50次，选择各算法精度最高的一次作为代表进行对比，遗传算法、粒子群算法和梯度混合粒子群算法的适应度收敛曲线如图9所示。

由图9可知，由于具有良好的初解，各算法收敛较快，但在收敛速度和求解精度上仍然存在差异，表4为50次仿真计算结果的统计值。

仿真结果表明，在求解星际探测轨道时，遗传算法收敛精度较高，粒子群算法搜索速度较快，梯度混合粒子群算法收敛速度最快，GHPSO相对GA提高61.87%，相对PSO提高43.66%；梯度混合粒子群算法精度最高，GHPSO相对GA平均精度提高了3.33%，最高精度提高了1.63%，相对PSO平均精度提高了4.72%，最高精度提高了3.02%。

本文提出的梯度混合粒子群算法，通过结合梯度搜索的特点使得粒子种群能跳出局部最优解，解决了粒子群算法易“早熟”的现象。仿真结果表明，该算法的全局寻优能力及收敛速度较传统遗传算法和粒子群算法都有了显著提高。

表 4 优化性能对比

5 结论

(1)本文提出了新的“星际高速公路”概念，旨在通过寻找合适的发射窗口，合理利用行星引力场，缩短深空探测需要耗费的时间。

(2)以多任务深空探测为背景，建立了包含多模型、多约束、多变量、多阶段的星际高速公路优化设计模型。

(3)通过融合推力工作模式、 分段设计目标函数等策略，克服了模型的内点约束限制，降低了优化模型的复杂度。

(4)为了提高优化速度、提升优化精度，结合梯度搜索和粒子群算法的特点，研究提出了一种梯度混合粒子群算法。

(5)横向对比了本文算法与传统粒子群算法和遗传算法的优化性能，仿真结果表明，本文提出算法搜索速度快，第一设计阶段GHPSO相对GA提高61.96%，相对PSO提高47.85%，第二设计阶段GHPSO相对GA提高61.87%，相对PSO提高43.66%；精度最高，第一设计阶段GHPSO相对GA平均精度提高了2.86%，最高精度提高了1.24%，相对PSO平均精度提高了4.19%，最高精度提高了3.97%，第二设计阶段GHPSO相对GA平均精度提高了3.33%，最高精度提高了1.63%，相对PSO平均精度提高了4.72%，最高精度提高了3.02%。

(6)优化得到了发动机的工作时序，发动机从66 844.4 MJD开机，持续工作397.41个儒略日；在67 241.85 MJD关机，持续关机382.89个儒略日；在67 624.74 MJD再次开机直至燃料消耗完毕。

[1] 吴伟仁,刘旺旺,蒋宇平,等.国外月球以远深空探测的发展及启示(上)[J].中国航天,2011(7):9-12.

[2] 吴青.飞出太阳系[J].大自然探索，2011(4):20-24.

[3] Cui P Y,Qiao D,Cui H T,et al.Target selection and transfer trajectories design for exploring asteroid mission[J].Science China Technological Sciences,2010,53(4):1150-1158

[4] 李鉴,韩潮.小推力最优轨道转移问题的UKF估计算法[J].宇航学报,2014,35(2):144-150

[5] 谭高威,高扬,杨新.深空探测器多次引力辅助转移轨道全局搜索[J].航天器工程,2012,21(2):18-27.

[6] David C F,Mark W,Kathleen H,et al.Applications of multi-body dynamical environments:the ARTEMIS transfer trajectory design[J].Acta Astronautica,2012,73(12):237-249.

[7] 孟林智,黄江川,叶培建,等.嫦娥二号卫星多目标多任务设计与经验[J].中国科学：技术科学,2013,43(6):585-595.

[8] 李俊峰,蒋方华.连续小推力航天器的深空探测轨道优化方法综述[J].力学与实践,2011,33(3):1-6.

[9] 尚海滨,崔平远,徐瑞,等.基于高斯伪光谱的星际小推力转移轨道快速优化[J].宇航学报,2010,31(4):1005-1011.

[10] 乔栋,崔平远,徐瑞.星际探测借力飞行轨道的混合设计方法研究[J].宇航学报,2010,31(3):655-660.

[11] Hartmann J W,Coverstone V L,Williams S N.Optimal interplanetary spacecraft trajectories via Pareto genetic algorithm[J].The Journal of the Astronautical Sciences,1998,46(3):267-282.

[12] Mateen-ud-Din Q,He Lin-shu,Tarek E.Rapid trajectory optimization using computational intelligence for guidance and conceptual design of multistage space launch vehicles [C]//AlAA Guidance,Navigation,and Control Conference and Exhibit,San Francisco,California,2005:1-18.

[13] 冉茂鹏,王青.一种基于EPSO的航天器交会轨迹优化方法[J].宇航学报,2013,34(9): 1195-1201.

[14] 唐金国,罗亚中,雍恩米.航天器轨道优化理论、方法及应用[M].北京: 科学出版,2011：169-180.

[15] 赵国强.深空探测飞行任务轨道设计[D].北京:清华大学，2011.

[16] 戴光明,彭雷,罗治情.行星际脉冲转移轨道设计与优化算法[M].武汉:中国地质大学出版社,2012.

[17] 汪定伟,王俊伟,王洪峰,等.智能优化方法[M].北京:高等教育出版社,2007.

[18] 鲜勇,许立军.遗传算法在导弹飞行程序设计中的应用研究[J].系统仿真学报,2009,21(5):1502-1504.

[19] 杨希祥,江振宇,张为华.基于粒子群算法的固体运载火箭上升段弹道优化设计研究[J].宇航学报,2010,31(5):1304-1309.

(编辑：吕耀辉)

Design of low-thrust multitask exploration orbit based on gravity-assist

LIN Hao-shen,HE Bing,ZHAO Xin,LIU Gang,AN Xi-bin

(Department of Space Engineering,The second Artillery Engineering University,Xi'an 710025,China)

Based on long time and high cost features of deep space exploration,an optimization model,containing multiple models,constraints,variables and multi-stage,was established.By integrating thrust mode and step-by-step design of objective function,the complexity of optimization model was reduced.In order to improve the speed and accuracy of optimization algorithms,a Gradient Hybrid Particle Swarm Optimization (GHPSO) algorithm was presented,which combined the characteristic of gradient search and Particle Swarm Optimization algorithm.This algorithm was applied to the trajectory optimization for multitask explorations to obtain engine's timing.Then the performance of GHPSO was compared with traditional particle swarm optimization(PSO)algorithm and genetic algorithm(GA).The results of simulation show that the GHPSO has faster convergence and higher accuracy. In the first stage of simulation,the convergence speed of GHPSO was 61.96% faster than GA and 47.85% than PSO,meanwhile,the average accuracy of GHPSO was 2.86% higher than GA and 4.19% than PSO,and the highest precision of GHPSO was 1.24% higher than GA and 1.63% than PSO.In the second stage,the convergence speed of GHPSO was 61.87% faster than GA and 43.66% than PSO,meanwhile,the average accuracy of GHPSO was 3.33% higher than GA and 4.72% than PSO,and the highest precision of GHPSO was 1.63% higher than GA and 3.02% than PSO.The result shows that the GHPSO can be applied to trajectory optimization design as well other nonlinear constrained global optimization problems.

gradient hybrid particle swarm optimization；multitasking interplanetary exploration；gravity-assist

2015-09-25；

2016-03-07。

基于量子生物地理优化的低空UAV编队在线协同航迹规划方法研究(61403399)。

林浩申(1992—)，男，硕士，专业方向为空间轨道设计与优化、空间信息融合。E-mail：linhaoshen1@163.com

V412

A

1006-2793(2017)01-0121-07

10.7673/j.issn.1006-2793.2017.01.022