基于RRLS的电网戴维南等值参数辨识研究

丁 蓝班诗淇曾 博

（1.国网四川省电力公司南充供电公司，四川 南充 637000；2.华北电力大学新能源电力系统国家重点实验室，北京 102206）

基于RRLS的电网戴维南等值参数辨识研究

丁 蓝1班诗淇1曾 博2

（1.国网四川省电力公司南充供电公司，四川 南充 637000；2.华北电力大学新能源电力系统国家重点实验室，北京 102206）

互联电网的规模不断扩大，为简化规模满足运算要求，戴维南等值广泛用于电力系统计算中。本文从戴维南等值参数获取方法进行分类，通过分析了戴维南等值模型以及参数的特点，讨论了利用端口电压电流数据的可辨识条件，进而提出了基于抗差递推最小二乘的戴维南等值参数辨识，抗差递推最小二乘算法能够有效地处理因为工况运行点过于接近所导致的戴维南参数漂移问题，同时能够有效并且具有一定抗干扰的参数跟踪能力。简单电路测试表明抗差递推最小二乘更够更快地反映参数变化，并且证明了其具备抗差性，同时四机两区域系统计算结果表明所提方法的有效性。

戴维南等值；参数辨识；抗差递推最小二乘

目前从电网戴维南等值参数的获取方法可以分为3类：①基于多点潮流观测方程的辨识法，文献[2-9]分别提出了卡尔曼滤波参数跟踪、两点及多点直接计算、卡尔曼滤波、最小二乘等方法对端口方程进行等值计算；②基于轨迹的构造比函数，文献[10-12]利用相近运行点的等值外端口特性相接近，对轨迹进行逼近求解，通过构建不同的曲线方程，利用运行相近而计算等值参数，而目前主要采用电压幅值曲线作为逼近对象；③基于递推修正类等值参数跟踪方法，文献[13-17]主要研究了偏差校正算法跟踪以及相关参数选取。戴维南等值参数辨识一般需要用到不同运行点的端口数据，存在因为运行点相近而导致 0/0数值不稳定，即参数漂移，另一方面又存在由于运行工况发生变化，等值参数也随着变化，即参数跟踪问题。

本文分析了戴维南等值模型以及参数的特点，讨论了利用端口电压电流数据的可辨识条件，进而提出了基于抗差递推最小二乘（robust recursive least square,RRLS）的戴维南等值参数辨识。抗差递推最小二乘算法能够有效地处理因为工况运行点过于接近所导致的戴维南参数漂移问题，同时能够有效并且具有一定抗干扰的参数跟踪能力。简单电路测试表明抗差递推最小二乘更够更快地反映参数变化，并且证明了其具备抗差性，同时四机两区域系统计算结果表明所提方法的有效性。

1 戴维南等值模型与物理意义

将待分析的电力系统划分为外部系统（E），边界系统（B）和内部系统（I），若只需要关注内部信息，则需要消去外部节点，保留边界和内部节点，如图1所示。

图1 等值示意图

完整系统的节点电压方程为

消去外部节点，保留边界和内部节点后的节点电压方程，即

戴维南等值方程为

除每年大量现场演出之外，巴尔迪还致力于钢琴唱片的录制。他曾录制《格里格钢琴及室内乐作品全集》《拉赫玛尼诺夫钢琴协奏曲全集》《舒曼钢琴作品全集》等大型录音合辑，以及《普朗克歌曲改编曲》《“李斯特读后感”》等单张专辑。目前，他正在录制《胡梅尔钢琴奏鸣曲全集》，其中前两张业已问世。

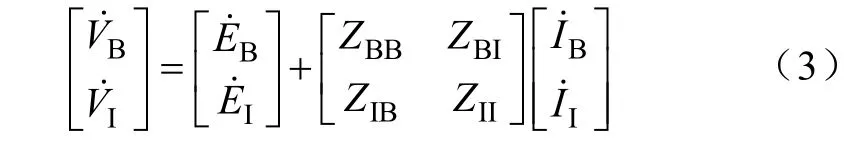
特别的，当从单个负荷节点观察电网时，即可等值为电压源串联阻抗与待研究的节点相联。

并且满足：

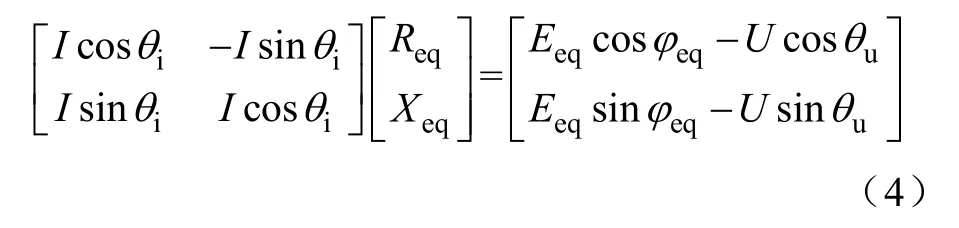
图2 端口等值模型

式中，Eeq、ϕeq分别表示等值电势的幅值、相位；θu、θi分别表示端口电压以及电流相位，Req、Xeq分别表示等值电阻与电抗。

由上分析可知：

1）对于注入量不变且拓扑参数不改变的系统，戴维南等值是严格的数学等值。

2）当能够实时获得戴维南等值参数，则戴维南等值具备动态跟踪意义。

2 基于RRLS的等值参数辨识

抗差递推最小二乘（robust recursive least square,RRLS）的核心思想是：每更新一次新的数据点，算法就会将所获数据经过抗差准则函数判定后，若为噪声数据进行抗差修正，若为正常数据则对结果进行更新[18]。由于该算法不是直接将新数据加入计算，因此历史数据的误差对辨识结果将不会增大。其数学描述为

式中，λ被称之为遗忘因子，其物理意义是对所参与计算的采样数据不同权重考量，基于需要追踪等值参数的变化，所以离当前时间越近的数据越能反映参数的变化状况，故而其权重也应该偏大。因此对有效数据采取渐消记忆的方式，将旧数据逐渐地遗忘掉。最新的一次采样数据加权为1，λ值通常取为0.95～0.99。ρ表示抗差准则函数，满足：

式中，δ是ε对应的标准差，i为ε的维数，Δ是用来调节递推的抗差性与有效性的正实数[14]，当观察误差存在大于Δδ时，ρ(ε)为一常数，即存在较大的预测误差出现时，其对目标函数的贡献固定在(Δδ)2/2，因此，其所带来的副作用将会被削弱。误差较小时，则为加权平方和最小，对辨识结果产生有益的贡献。特别地，通常认为噪声满足为高斯分布，因此取Δ=3，因此在已知道第l次参数辨识结果，建立l+1次采样数据抗差递推：

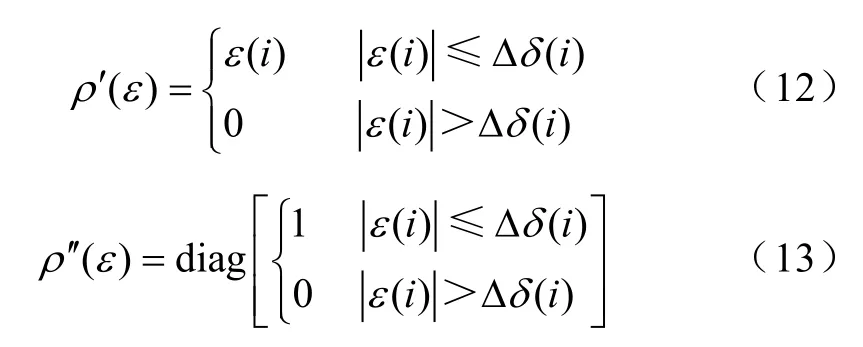
标准差δ的取值可由误差传递式获得，如对于电流的实部和虚部间接测量误差方差[18]：

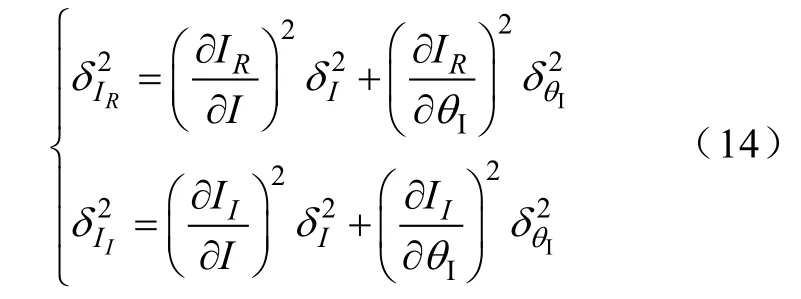
3 算例验证

3.1 简单电路测试

简单电路测试对象，电源电势 100V，阻抗为5+j20Ω，改变端口负荷阻抗由 j101～j250，变化时间步长0.1s，阻抗变化步长j1，变化时间15s。测试结果如图3所示，图中实线代表本文所提RRLS等值跟踪，虚线代表文献[17]所提出偏差校正的等值跟踪。可以看出RRLS经过初值优化后可以快速进入等值跟踪，并且比文献[17]所提方法达到稳定状态更加迅速，明显提高了跟踪速率，并且保持数值稳定性。

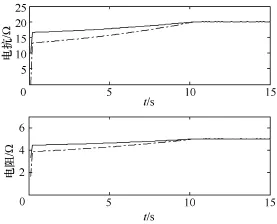
图3 简单电路跟踪性能测试结果之阻抗

对端口电压电流量幅值加入 0.1%的高斯白噪声，等值跟踪辨识结果如图4所示，图中实线代表本文所提 RRLS等值跟踪，虚线代表文献[17]所提出偏差校正的等值跟踪。

图4 加入0.1%噪声等值参数辨识结果

由图 4可以看出，RRLS在噪声的作用下，具有较强的抗差性能，辨识结果更加稳定。

3.2 四机两区域系统测试

测试系统采用文献[17]中仿真系统，如图 5所示，对区域1进行系统等值，改变母线9的负荷（仿真第5s开始均匀增加有功无功负荷，直到10s）针对区域1系统，即节点6背后系统进行RRLS戴维南等值跟踪，等值阻抗结果如图6所示。

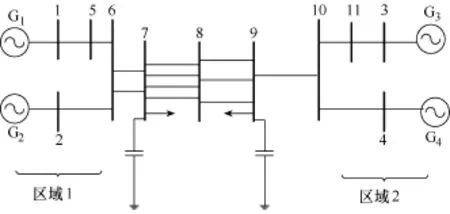
图5 四机两区域系统

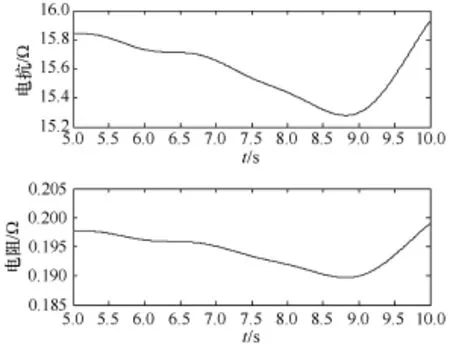
图6 四机两区域系统跟踪等值阻抗

对于节点6的边界自导纳：

节点6外部区域1自导纳矩阵：

节点6与区域1互导纳矩阵：

式中，Y(i,j)表示节点i、j之间节点互导纳，Y(i,i)表示节点i的自导纳，YG1、YG2分别为G1、G2的等值导纳。由式（2）可以计算出区域1等值阻抗为0.2117+ j15.8916Ω。

通过RRLS的戴南等值参数跟踪辨识可知，等值电阻 0.19～0.2Ω之间变化，等值电抗在 j15.3～j15.9Ω之间变化，与基于静态等值计算结果基本一致的。但是值得注意的事由于利用实测数据进行参数辨识，等值阻抗也体现了算法对动态参数跟踪能力，能够更加准确反映系统运行工况的变化，因此基于RRLS的戴维南等值参数跟踪辨识是有效。

4 结论

本文提出基于抗差递推最小二乘的戴维南等值参数辨识，抗差递推最小二乘算法能够有效地处理因为工况运行点过于接近所导致的戴维南参数漂移问题，同时能够有效并且具有一定抗干扰的参数跟踪能力。等值参数跟踪性能测试证实了抗差递推最小二乘更够更快地反映参数变化，并且具备抗差性。而四机两区域系统计算结果表明所提方法的有效性。

[1]周念成,廖彦洁,颜伟,等.基于相量测量的电压稳定裕度计算及减载方案[J].中国电力,2012,45(5):6-10.

[2]庞晓艳,周剑,颜伟,等.基于最小二乘外网等效的线路电压稳定性指标[J].中国电力,2011,44(4):21-25.

[3]Ohtsuka K,Yokokawa S,Tanaka H,et al.An equivalent of multi-machine power systems and its identification for on-line application to decentralized stabilizers[J].IEEE Transactions on Power Systems,1989,4(2):687-693.

[4]廖国栋,王晓茹.电力系统戴维南等值参数辨识的不确定模型[J].中国电机工程学报,2008,28(28):74-79.

[5]李来福,柳进,于继来,等.节点戴维南等值参数在线跟踪简捷算法[J].中国电机工程学报,2006,26(10):40-44.

[6]安天瑜,周苏荃.一种电压薄弱负荷节点群的戴维南等值参数跟踪方法研究[J].继电器,2007,35(24):21-25.

[7]罗华伟,吴政球,戴庆华,等.电网戴维南等值参数的快速计算[J].中国电机工程学报,2009,29(1):35-39.

[8]赵金利,余贻鑫,Zhang Pei.基于本地相量测量的电压失稳指标工作条件分析[J].电力系统自动化,2006,30(24):1-4,10.

[9]闫常友,刘建飞,杨奇逊,等.基于平方根滤波的网络等值算法[J].继电器,2006,34(3):41-46.

[10]王漪.柳焯.基于戴维南等值的系统参数跟踪估计[J].电网技术,2000,24(11):28-30.

[11]王芝茗,王漪,徐敬友,等.关键负荷节点集合电网侧戴维南参数预估[J].中国电机工程学报,2002,22(2):16-20.

[12]李娟,刘修宽,曹国臣,等.一种面向节点的电网等值参数跟踪估计方法的研究[J].中国电机工程学报,2003,23(3):30-33.

[13]Corsi S,Taranto G N.A real-time voltage instability identification algorithm based on local phasor mea-surements[J].IEEE Transactions on Power Systems,2008,23(3):1271-1279.

[14]Corsi S.Wide area voltage protection[J].IET Gener.Transm.Distrib,2010,4(10):1164-1179.

[15]牟善科,丁涛,顾伟,等.基于偏差校正的戴维南等值参数在线跟踪改进算法[J].电力系统保护与控制,2011,39(2):23-28.

[16]Arefifar S A,Xu W.Online tracking of power system impedance parameters and field experiences[J].IEEE Transactions on Power Delivery,2009,24(4):1781-1788.

[17]丁蓝,王先洪,欧智乐,等.初值优化的电力系统戴维南等值跟踪算法研究[J].中国电力,2013,46(9):102-106.

[18]丁蓝.基于PMU的输电线路参数辨识与戴维南等值研究[D].北京:华北电力大学,2012.

Research on Thevenin Equivalent Parameters Identification based on Robust Recursive Least Square

Ding Lan1Ban Shiqi1Zeng Bo2
(1.Nanchong Electric Power Bureau,Nanchong,Sichuan 637000；2.State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University),Beijing 102206)

The thevenin equivalent is widely used in power system calculation for simplifying the scale.In this paper,thevenin equivalent parameter acquisition method is reviewed and the model characteristics are analyzed.Then,robust recursive least square is presented to track thevenin equivalent parameter considering numerical instability and the changing operating point of power gird.At last,the tracking performance test and four-machine two-area system simulation prove the validity and stability of the proposed algorithm.

thevenin equivalent；parameter identification；robust recursive least square

丁 蓝（1987-），男，硕士，工程师，主要研究方向为电力系统保护与控制。