基于组合预测模型的电动汽车充电站短期负荷预测研究

陈希强刘志欣李兴波

（1.山东电力公司泰安供电公司，山东 泰安 271000 2.山东电力公司高密供电公司，山东 高密 261500 3.山东电力公司平阴供电公司，山东 平阴 250400）

基于组合预测模型的电动汽车充电站短期负荷预测研究

陈希强1刘志欣2李兴波3

（1.山东电力公司泰安供电公司，山东 泰安 271000 2.山东电力公司高密供电公司，山东 高密 261500 3.山东电力公司平阴供电公司，山东 平阴 250400）

针对电动汽车充电站充电功率随机性大的难题，本文建立了 ELMAN反馈式神经网络预测模型，然后采用粒子群算法对其进行优化，接着将优化之后的模型与模糊控制相结合，最终建立 3种模型相结合的组合预测模型，并以青岛地区某一充电站的实际负荷数据为算例，验证了组合预测模型的有效性，提高了电动汽车充电站短期负荷预测的精度。

ELMAN神经网络；粒子群算法；模糊控制；组合预测模型；短期负荷预测

电动汽车的快速发展给电网带来巨大的冲击，尤其在短期负荷预测领域，电动汽车充电负荷的随机性非常大，给短期负荷预测带来困难[1]，为了提高短期负荷预测的精度，有必要对电动汽车充电站单独进行短期负荷预测。目前关于电动汽车充电站短期负荷预测的研究历史不长，国内外学者主要研究思路为：首先分析负荷数据，选出相关性较大的影响因子，然后选择神经网络、支持向量机等单一模型及其改进模型建立预测模型，预测精度有所保障，但仍有待进一步提高。

神经网络模型具有自我学习能力强、能够较好逼近任意非线性函数的优点，在电动汽车充电站短期负荷预测领域仍是一种有效的预测方法。其中，ELMAN神经网络属于反馈式神经网络，能够将前一时刻隐含层的输出结果保存下来，具有更好的动态控制效果。

ELMAN神经网络模型在训练过程中将误差反向传播，计算出的误差梯度是近似值，难免影响权值的调整，而粒子群算法是一种寻优方法，具有良好的全局搜索能力，能够有效解决模型陷入局部最优的问题。采用粒子群算法对ELMAN神经网络进行优化，能够更好的训练网络，快速优化出网络最佳权值。

神经网络虽然能够处理任意非线性问题，但无法证明其推理过程，而模糊控制的推理能力强，能够模仿人脑功能，处理只能依靠经验判断而无法依靠公式表述的问题。因此，将模糊控制引入神经网络模型中，从而使预测模型具有两者共同的优势。

本文考虑了ELMAN神经网络、粒子群优化算法以及模糊控制3种模型，最终建立了基于三者的组合预测模型，实现了3种模型之间的优势互补，同时更加全面的考虑了负荷数据、日类型、气象状况等影响因素，预测结果表明，组合预测模型能够有效提高预测精度。

1 ELMAN神经网络原理

1.1 ELMAN神经网络的网络结构

ELMAN神经网络结构示意图如图1所示。

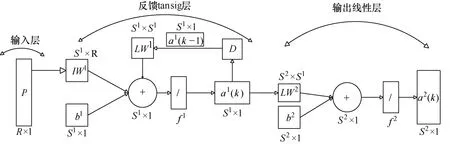
图1 ELMAN神经网络结构示意图

图1中，神经网络模型的输入为P，为R维向量，隐含层输出为 a1，为 S1维向量，输出层输出为a2，为 S2维向量， IW1为输入向量到隐含层神经元的权值矩阵，为 S1×R维矩阵， LW1为反馈层神经元到隐含层神经元的权值矩阵，维数为 S1×S1维矩阵， LW2为隐含层到输出层的权值矩阵，为 S2×S1维矩阵，b1、b2为阈值，分别为 S1、S2维向量， f1、f2分别为隐含层传递函数、输出层传递函数。

ELMAN神经网络两层神经元的输出与输入关系式为

1.2 学习算法

ELMAN神经网络是在BP神经网络的基础上发展而来的，在一些近似简算的过程中，采用与静态BP神经网络相同的方法修正权值，在精确计算时则不可，需要考虑动态学习规则修正权值。BP与ELMAN两种网络的学习算法都是链式法则，但不同之处为BP网络为无序的，而ELMAN网络为有序的。另外一个不同点是ELMAN神经网络在训练过程中采用在线训练规则。

误差函数 E为某一时刻（k时刻）权值修正的依据函数，即

网络权值的修正公式为

式中，w可以代表输入层到隐含层和隐含层到输出层的权值。

采用有序链式法则，对于隐含层到输出层权值，则有

同样采用有序链式法则，对于输入层到隐含层的权值，则有

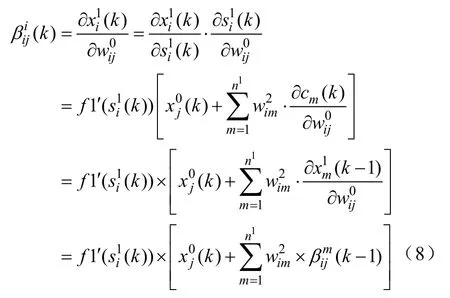
从而可以得到

同理可得关联层的权值，即

2 粒子群算法优化ELMAN神经网络预测型

粒子群（particle swarm optimization，PSO）算法的提出来自于人类对于鸟群寻找食物这一社会群体行为的研究与模仿，是一种通过模拟鸟群寻找食物这一常见动物行为而逐渐形成的基于群体协作的随机搜索算法，现在广泛用于解决智能优化问题。

粒子群算法优化神经网络可以有多种方式[2]，本文采用优化ELMAN神经网络的权值，优化模型的关键在于粒子群算法适应度函数的选取和编码方式的确定。首先，适应度函数仍然选择神经网络的性能函数—mae函数，通过粒子群算法寻找一组合理的权值，以使mae函数的结果最小，即网络训练误差最小。适应度函数公式为：

式中，F为适应度；N为样本数；y为预测输出；t为实际输出。

对于编码方式，为了确定粒子群算法中待优化的变量，需要确定神经网络结构，输入维数记为Indim ，隐层神经元数目记为Hiddendim ，输出层神经元数目记为Outdim，则输入层至隐层权值维数W1、隐层至隐层权值的维数W2、隐层至输出层权值的维数W3分别为

每一个粒子的维数D为

适应度函数和编码方式确定之后，便可建立粒子群算法优化ELMAN神经网络模型，PSO算法优化ELMAN神经网络模型算法流程图如图2所示。

图2 PSO算法优化ELMAN神经网络模型算法流程图

3 融入模糊控制的组合预测模型

3.1 模糊控制原理

模糊控制由模糊集合论、模糊语言变量、模糊逻辑推理三部分组成，是一种智能控制方法，利用人的经验知识对问题进行处理，针对无法建立数学模型的复杂问题，普通自动控制系统可能出现既属于A又属于B的多种选择，从而影响控制过程的下一步选择，而模糊控制则可以明确下一步过程的选择，具有模糊处理问题的能力，模糊控制原理图如图3所示。

图3 模糊控制原理图

图中，知识库、模糊化、模糊推理和非模糊化4部分共同组成模糊控制器，作为模糊控制的核心，图3中，E为误差信号，e为模糊集合，u为模糊输出，U为模拟输出量。通过不断对控制量进行采样，并输入模糊控制器中，可得到高精度的控制量，减小偏差。

3.2 PSO-ELMAN神经网络与模糊控制组合预测模型

模糊控制与神经网络的结合方式有多种方式[3-5]，本文采用模糊控制系统优化ELMAN神经网络预测结果，这对于预测精度的提高效果显著，预测模型如图4所示。

图4 PSO优化ELMAN神经网络与模糊控制组合预测模型图

图4中，t表示预测时间点，Y(t)为PSO-ELMAN神经网络模型预测值，∑表示求和，R(t)为预测点实际负荷值，E(t)为当前预测点PSO-ELMAN神经网络模型预测误差，E(t−1)为前一预测点PSO-ELMAN神经网络模型预测误差，EC(t)为误差变化，EC(t)=E(t)−E(t−1)。X(t)为负荷修正量，y(t+1)为输出预测值（注意y(t+1)=Y(t+1)+X(t)）。由图4可知，PSO-ELMAN神经网络与模糊控制组合预测模型采用模糊控制优化神经网络运行结果的组合方式，模糊控制系统通过对PSO-ELMAN神经网络模型的预测误差E(t)以及前一预测时间点PSO-ELMAN神经网络模型预测误差E(t−1)进行采集，得出负荷修正量X(t)，对下一时刻PSO-ELMAN神经网络模型预测值Y(t−1)进行修正，得出输出预测值。

图4组合预测模型中，模糊控制器一旦设计完成，无需进行内部操作，可看做一个黑匣子，只需输入邻近预测点的预测误差E(t)、E(t−1)，便可对下一时刻负荷预测值进行修正。模糊控制器设计步骤如下文所述。

1）确定输入输出

模糊控制器有许多类型，根据输出维数的不同可以分为单维输出和多维输出，考虑到PSO-ELMAN神经网络采用1维输出，所以模糊控制器相应的取单维输出。模糊控制器的输入维数取为2，以PSO- ELMAN神经网络模型预测误差E以及误差变化EC为输入。输出为修正因子a，则下一时刻的负荷预测值Y的修正量X为

式中，a，b为误差和误差变化的修正因子，且a+b=1；a,b∈(0,1)。

2）模糊化处理

对于输入量E、EC和输出量a，需要分别确定自己的模糊论域、模糊语言值以及隶属度函数。模糊论域、模糊语言值、隶属度函数三者均可以人为设定，本文如此设定：

E模糊论域为E={−4,−3,−2,−1,0,1,2,3,4}。

EC模糊论域EC={−4,−3,−2,−1,0,1,2,3,4}。

a模糊论域为a={0,0.25,0.5,0.75,1}。

E模糊语言值为NB、NS、ZO、PS、PB（分别表示负大、负小、零、正小、正大）。

EC模糊语言值为NB、NS、ZO、PS、PB（分别表示负大、负小、零、正小、正大）。

a模糊语言值为VS、S、M、B、VB（分别表示负大、负小、零、正小、正大）。

隶属度函数是将变量的模糊语言值映射到模糊论中，与普通函数的区别在于隶属度函数允许是一对多，隶属度函数通过隶属度的值确定因变量。隶属度函数有多种表示方法，本文采用三角形隶属函数，分别如图5和图6所示。

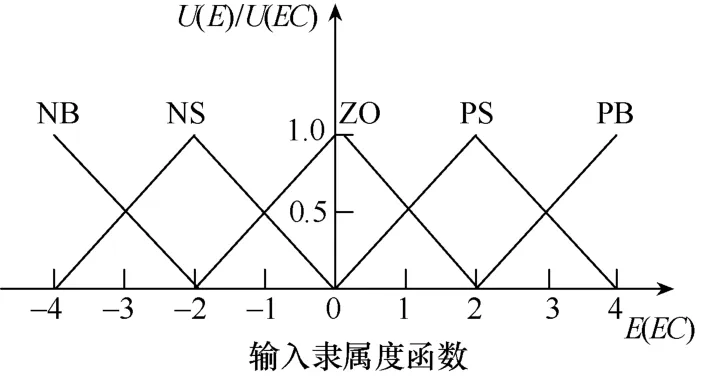
图5 三角形输入隶属度函数图

图6 三角形输出隶属度函数图

3）模糊规则设定

模糊规则采用“if ...then...”的格式存储，例如：if E is NB and EC is ...then a is VS.译为当误差太大，预测值远远大于实际值时，无论误差变化的趋势如何，都应当使下一时刻的预测值减小，所以修正因子应当尽可能的减小。根据类似的逻辑推理，可以得出其他模糊规则，本文建立模糊规则表见表1。

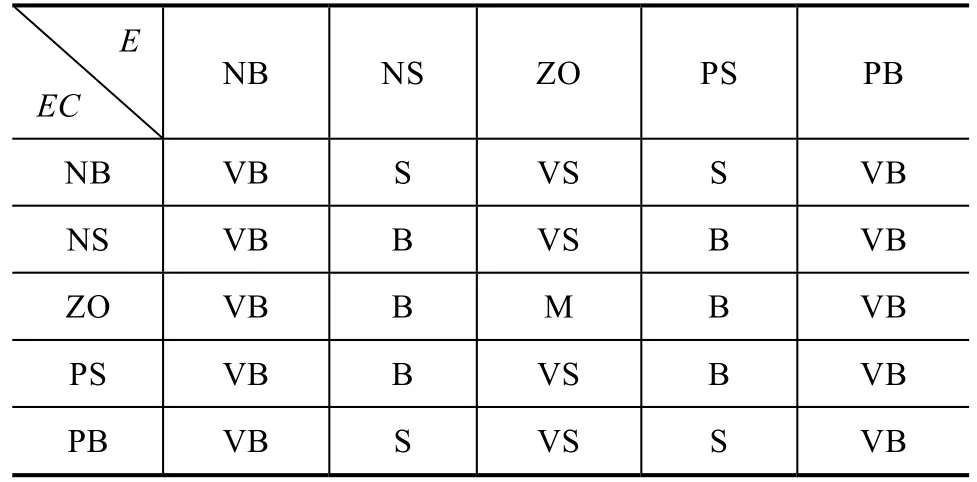
表1 输出a的模糊控制规则表

4）反模糊化

通过模糊规则进行模糊控制之后，将输出进行反模糊化得出最终的输出量，反模糊化方法有多种，本文采用经典的 Mamdani极大极小推理法和重心法[6]进行反模糊化操作，此法具有简单易行、可图形化等优点。具体过程如下文所述：为模糊论域中的某一个值，则三元模糊关系即可得出：

因此a的隶属度则成为

以上过程即为Mamdani推理法求取输出a的隶属度的方法，其结果为模糊化之后的结果，然后用重心法求出输出a的精确值，重心法的计算公式为

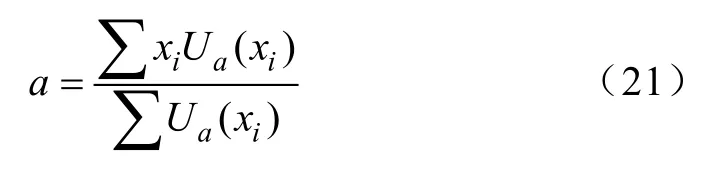
式中，xi为输出a所对应的模糊论域中的某一个值，为输出a的隶属度。

4 仿真算例

4.1 样本处理

本文考虑了气象类型、温度、日类型、负荷数据4部分内容作为影响因素，气象类型可以根据降雨的概率进行归一化处理，可能性大的诸如大中小雨、雪，阵雨，雷雨等天气，记为 1，其他类型记为0。

对于温度数据，同样需要对其进行归一化处理，线性式为

式中，Tmax、Tmin分别为整个样本中的最高温度和最低温度，T、t分别为处理前、后的数据。

对于日类型数据，由于工作日与非工作日人们的出行情况差别较大，必须考虑，工作日样本记为1，非工作日记为0。

以青岛地区某一电动汽车充电站 2013年的历史负荷数据为样本，对负荷数据进行预处理，首先剔除不合理的数据以及坏掉的数据，然后根据历史数据样本表格的上下左右4个数据进行平均求值，以此作为剔除数据的补充。

4.2 模型参数选择

ELMAN神经网络参数设定：迭代次数取1000，误差目标取 0.001，总样本数取 10，样本输入维数取24，三层神经元数目分别取24、9、1，两层传递函数分别为“tansig、logsig”。

粒子群算法参数设定：ω初值取0.9，c1,c2取2，种群规模P取40，迭代次数T为100，1r，r2取[0,1]内的随机数。

模糊控制器参数设定：最大误差Emax取 2，最大误差变化取 2，修正量初值X0为 0，误差变化初值EC0为0。

4.3 仿真结果

由于季节的不同对电动汽车充电站负荷的影响不同，本文选择秋季和冬季两个季节的数据进行仿真，仿真结果分别见表2和表3。

表2 秋季预测日四种模型预测误差对比表/%

表3 冬季预测日四种模型预测误差对比表/%

5 结论

本文以ELMAN神经网络为基础，采用粒子群算法对其优化，优化后的预测模型又与模糊控制建立了组合预测模型，仿真结果表明，对于秋季预测日，采用PSO单独优化ELMAN神经网络，误差可以减少1.1%，而融入三种模型的组合预测模型，可以将误差进一步减小0.8%；对于冬季预测日，采用PSO单独优化 ELMAN神经网络，误差可以减少0.9%，而融入三种模型的组合预测模型，可以将误差进一步减小0.9%。由于冬季电动汽车负荷数据的随机性更大的缘故，组合预测模型对于秋季预测日和冬季预测日的预测误差仍存在约2%的差距，但并不影响说明组合预测模型的有效性。

[1]张维戈,颉飞翔,黄梅,等.快换式公交充电站短期负荷预测方法的研究[J].电力系统保护与控制,2013(4):61-66.

[2]Bahrami S,Hooshmand R A,Parastegari M.Short term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization) algorithm[J].Energy,2014,72(7):434-442.

[3]Ahmmed S,Khan M A,Hasan M K,et al.STLF using Neural Networks and Fuzzy for anomalous load scenarios-A case study for Hajj[C]//International Conference on Electrical and Computer Engineering,2010:722-725.

[4]Jain A,Jain M B.Fuzzy Modeling and Similarity Based Short Term Load Forecasting Using Swarm Intelligence-A Step Towards Smart Grid[J].Advances in Intelligent Systems &Computing,2013,202:15-27.

[5]Rejc M,Einfalt A,Gawron-Deutsch T.Short-term aggregated load and distributed generation forecast using fuzzy grouping approach[C]//International Symposium on Smart Electric Distribution Systems and Technologies.IEEE,2015.

[6]陈阳,王涛,刘玉航.二型模糊集下的推理模型及Mamdani推理算法[J].模糊系统与数学,2008,22(3):41-48.

Research of Short-Term Load Forecasting for Electrical Vehicle Charging Station based on Combined Prediction Model

Chen Xiqiang1Liu Zhixin2Li Xingbo3
(1.Taian Power Supply Company of Shandong Power Company,Taian,Shangdong 271000 2.Gaomi Power Supply Company of Shandong Power Company,Gaomi,Shangdong 261500 3.Pingyin Power Supply Company of Shandong Power Company,Pingyin,Shangdong 250400)

The electrical vehicle charging station has a problem of big randomness.In order to solve this problem,this article sets up the ELMAN neural network prediction model.Then this article optimizes the model by Particle Swarm optimization.Then this article combines the optimized model with fuzzy control,and sets up a combined prediction model based on three models.This article collects the real load data of a electrical vehicle charging station in Qingdao.Lastly,results show that the above combined prediction model is effective,and this combined prediction model can improve the predict accuracy.

ELMAN neural network;particle swarm optimization;fuzzy control;combined prediction model;short term load forecasting

陈希强（1990-），男，山东省泰安市人，硕士研究生，主要研究方向为电力系统分析与控制。