计及随机性的电网低频振荡实时修正控制研究

宗鹏鹏 王培秀 闫济红 杨钦臣 吴健超

（东南大学电气工程学院，南京 210096）

计及随机性的电网低频振荡实时修正控制研究

宗鹏鹏 王培秀 闫济红 杨钦臣 吴健超

（东南大学电气工程学院，南京 210096）

本文主要研究电力系统发生低频振荡后的实时稳定性控制，分析了计及随机性的情况下概率阻尼比分布的变化，在半不变量法的基础上推导了计算方法。基于概率阻尼比以及阻尼比灵敏度，对控制措施进行量化，以确定最优控制措施，包括控制选址和控制量的确定。在两区四机系统中进行了仿真，验证了实时修正控制的有效性，与传统低频振荡控制措施相比，所提出的方法考虑了随机性，并且对控制措施进行了量化。这种方法能有效抑制系统的振荡模态。

半不变量法；概率分析；低频振荡；阻尼比灵敏度

随着大区联网，我国电力系统中低频振荡现象逐年增多，其严重性甚至超过了暂态稳定性，成为系统安全稳定运行的主要障碍[1]。低频振荡与系统的小干扰稳定性密切相关，目前的电网调度部门通常会针对电力系统的典型运行方式进行小干扰稳定分析校验，只有具有一定稳定裕度的运行方式才可能被采用。由于风电等可再生能源的快速发展、需求侧响应等原因，系统实际运行工况的随机性和波动性都日益明显。上述不确定性因素将导致系统发生低频振荡的风险明显增大，关系到电网的安全稳定运行。然而，如果将各种可能的不确定性因素都用确定性方法加以校验，那么计算量十分巨大，难以应用于实际电网。概率稳定性分析弥补了确定性方法的局限性，因而在电力系统动态稳定分析中有广泛的应用前景。

有关人员在电力系统低频振荡研究方面已经开展了较多工作，部分文献的研究基于确定性场景背景。文献[2]根据振荡中心的信息对设备进行分群，进而匹配主导模式，确定对应的控制措施；文献[3]分析了确定性情况下各个系统参数对电网小干扰稳定性的影响；文献[4]对储能系统提高系统低频振荡稳定的机理进行研究，研究了储能元件阻尼转矩的产生、传递、分配及影响模态阻尼的机理；文献[5]基于模态对运行方式和运行参数灵敏度，对控制措施加以量化。随着现代电力系统的不断发展，电网运行过程中出现了越来越多的不确定性因素，使得确定性的方法得到的结论在实际电网中往往有局限性。

目前国内外低频振荡概率稳定性的研究也有一定进展。文献[6]采用概率特征根分析的方法，比较了含附加阻尼控制器前后主要的概率特征根的变化；文献[7-8]采用蒙特卡洛模拟方法进行概率小干扰稳定性分析，耗时严重；文献[9]采用伊藤公式判别小干扰稳定性，并用矩稳定性刻画小扰动稳定性；文献[10]采用概率特征根的方法研究电力系统稳定器参数设计，使得PSS具有在较宽系统运行方式下的整体合理性。该方面的研究工作大多针对抑制低频振荡发生，聚焦于离线预防控制。

本文在计及随机性的基础上，对电力系统发生低频振荡后的实时修正控制展开研究。基于半不变量法和Gram-Charlier级数展开方法，提出了实时修正控制优化方法，减少了计算量，以适应实时控制的要求，并通过算例阐述了实时修正控制的步骤，证明了该方法的有效性。

1 常规的确定性修正控制

系统发生低频振荡后，主要基于运行人员的经验，有选择性的减小某些机组的出力以消除低频振荡。在常规的确定性修正控制[5]中，通过特征根的灵敏度合理的选择减出力的机组，得到有效的调整措施。

阻尼比通常用来衡量电力系统小干扰的稳定性，是分析和平息电力系统低频振荡的重要指标，对于系统中某一个弱阻尼或者负阻机电振荡模式，其对应的状态矩阵的特征值为λ，那么该特征值得阻尼比为

式中，Re和Im分别表示复数的实部和虚部，根据自动控制原理，当阻尼比大于零时，系统小干扰稳定，低频振荡会逐渐平息。实际应用中，一般给定系统中最弱阻尼比不小于 0.1～0.3。阻尼比对系统运行方式的灵敏度可以通过下式求得

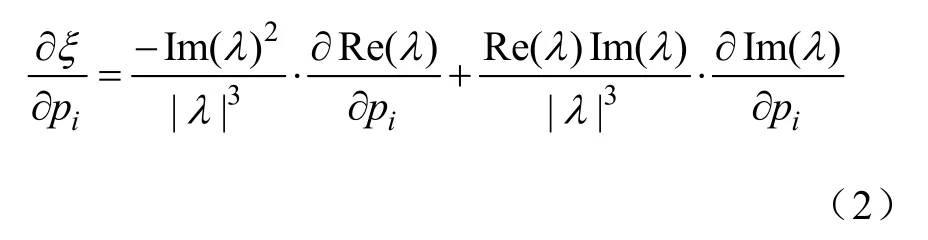
2 计及随机性的实时修正控制

2.1 概率阻尼比

随着风电的接入、负荷的波动以及运行方式的调整，系统的特征根也出现随机性。负荷的不确定性可以通过负荷曲线来描述，从而可以求得负荷的均值与方差，还可以求得发电机出力的均值和方差。所有的节点电压（V）、节点注入（S）和特征根（λ）都被认为是随机变量。本节的目的是确定系统阻尼比的灵敏度和它的方差。

在考虑多种运行状态时，系统稳定的程度取决于阻尼比ξ 的概率分布。而系统的阻尼比可以表示为

式中，0ξ为系统稳定运行点的对应模态的初始阻尼比，Δξ是考虑电力系统随机性后系统阻尼比的变化量，其可以被表示为

式中，S0称为阻尼比灵敏度矩阵，考虑注入量的随机性，通过半不变量法和级数展开可以很容易求得阻尼比变化量的概率分布，其期望和标准差分别可以写成和σΔξ。式（5）为一组线性变换，按式中的计算方式求取阻尼比变化量Δξ需要进行随机变量的卷积计算，计算量很大，不利于实时计算。通过引入半不变量与Gram-Charlier级数展开方法，可以通过半不变量的简单代数运算获得随机变量的概率分布。

节点i注入功率的随机扰动ΔiP主要由该节点发电机注入功率和负荷注入功率的随机量决定，即

式中，ΔPGi和ΔPLi分别为发电机和负荷注入功率的随机变量，符号∗代表卷积运算。

根据半不变量的齐次性和叠加性[11]，可以将式（6）转换为半不变量的代数运算，以减少计算量，满足实时计算要求，从而得到节点注入量的各阶半不变量，即

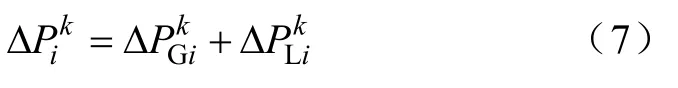
通过半不变量和中心距的关系以及级数展开式，可以得到Δξ的分布，从而得到Δξ的期望和方差[12]。本文采用Gram-Charlier级数展开式，这种级数的方法是把随机变量的分布函数表达为服从正态随机的变量各阶导数组成的级数，其中级数的系数可以用随机变量的各阶半不变量表示为

计及随机性的低频振荡修概率阻尼比计算流程图如图1所示。

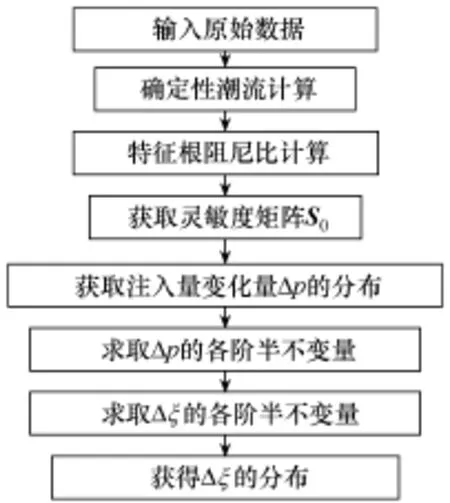
图1 概率阻尼比计算流程

2.2 实时修正控制措施

由上一节可以得Δξ的分布，通过概率统计的相关知识，可以定义边界阻尼比系数ξ′，满足ξ ξ′＞时的概率大于 0.95，当时系统小干扰稳定，此时认为低频振荡在该条件下能随机稳定[13-15]。

采取实时修正控制措施抑制低频振荡，涉及两个方面的内容：①减出力机组的选取；②减出力量化的确定。在电网已出现低频振荡的紧急状态之后，一般情况下减出力可以满足稳定要求，本文为了充分论证方法的有效性和正确性，同时采取了减出力和减负荷两项措施，以抑制系统振荡。

阻尼比灵敏度S0中较大的元素对应节点的发电机对阻尼比的影响较大，因此出力调整机组的选取可以由中S0元素的大小来确定。当采取实时修正控制措施时，除控制节点外，其余节点变化为零，此时阻尼比的变化和相应节点出力的变化关系可表示为

式中，ΔξGL为由于采取实时修正控制阻尼比的变化量；ΔPG和ΔPL分别为需要调整的发电机和负荷节点有功变化，为保证系统有功平衡，一般取ΔPG和相等。

为保证系统稳定，应满足随机稳定的条件，即

因此实时修正控制有功调整可以表示为

具体控制措施如下。

步骤 1：输入原始数据，在稳定点进行潮流计算；

步骤 2：通过摄动法求得特征根灵敏度，进而得到相关阻尼比的灵敏度矩阵S0；

步骤3：由初始数据得到注入量变化量ΔP的随机分布，得到ΔP的半不变量；

步骤 4：由ΔP的半不变量得到阻尼比变化量Δξ的半不变量，进而得到Δξ的分布，包含均值和方差；

步骤 5：根据式（12）确定相应节点减出力的量ΔpG。

3 算例分析

3.1 两区四机系统算例

为验证所提方法的准确性与实用性，本文以两区四机系统为例，其系统结构如图2所示，基本参数见文献[11-16]。

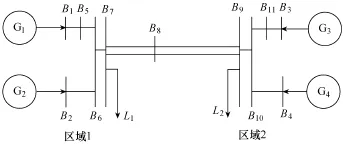
图2 两区四机系统网络图

通过频域分析发现，该系统存在3种低频振荡模式，有一个区域振荡模态和两个局部振荡模态，见表 1。其中区域模式阻尼比最小，严重影响联络线传输功率。

表1 系统存在的模态

在不考虑随机性的情况下，在仿真0.5s时系统8号节点受到一个小的干扰，发生接地短路故障，0.1s后短路故障消除，此时系统将发生低频振荡，如果此时不采取有效措施，系统就将逐步失去稳定，发电机1和发电机3间的功角的变化曲线如图3所示。

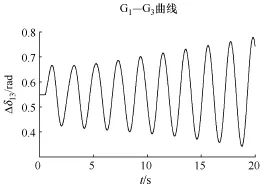
图3 不计随机性低频振荡功角图

下面将从3种场景来验证所提实时修正控制措施的有效性。场景一：不考虑系统的随机性，当系统发生低频振荡时及时采取常规的确定性修正控制；场景二：考虑系统的随机性，发生低频振荡时依然采取常规的确定性修正控制；场景三：考虑系统的随机性，发生低频振荡时及时地采取本文提出的计及随机性的实时修正控制。

1）在场景一的情况下，系统受到小干扰发生低频振荡时，及时采用常规的确定性修正控制，根据特征根灵敏度计算后，在发电机 1处减出力151MW，相应地负荷节点9处减负荷，通过系统仿真，此时发电机1和发电机3间的功角的变化曲线如图4所示。

图4 不计随机性常规修正控制功角图

由图4可以看出，在不考虑随机性的情况下，通过减出力和降负荷的常规修正控制措施，系统将逐步恢复稳定。这表明在不考虑随机性的基础上，常规的确定性修正控制可以平息系统的低频振荡。

2）在场景二的情况下，在上一小节的基础上，引入随性性，假设发电节点中1、2为风机接入点，其他发电机为常规机组。风机有功出力服从正态分布，其中Pgen为发电机基态有功值。常规机组出力保持恒定。另外，假设系统中的负荷服从正态分布其中Pload为负荷基态有功值[17-18]。

此时，同样采取常规的确定性修正控制，在发电机1处减出力151MW，相应地负荷节点9处减负荷，对上述系统采用仿真，此时发电机1和发电机3间的功角的变化曲线如图5所示。

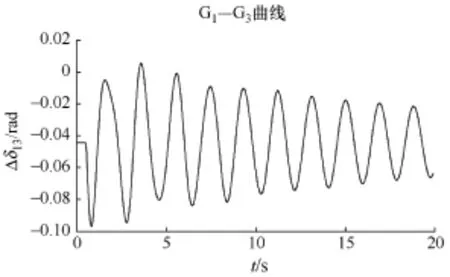
图5 计及随机性的常规修正控制功角图

由图5可以看出，考虑系统随机性的影响情况下，在采用常规的修正控制后，发电机1和发电机3之间的功角依然震荡，不能及时平息低频振荡，因此可以认为在考虑随机性的情况下，常规的低频振荡措施失效了。

3）在场景三的情况下：首先，各个稳定点进行线性化，求得系统的线性化方程。在考虑随机性的基础上，求得系统的边界阻尼比，在满足系统随性稳定的情况下，制定实时修正控制措施，在1号发电机处紧急减235MW出力，同时在节点9处减负荷。通过仿真可以看出在采取紧急控制减小出力和负荷之后，阻尼比保持在合理的范围之内，此时发电机1和发电机3间的功角的变化曲线如图6所示，系统低频振荡逐渐平息。

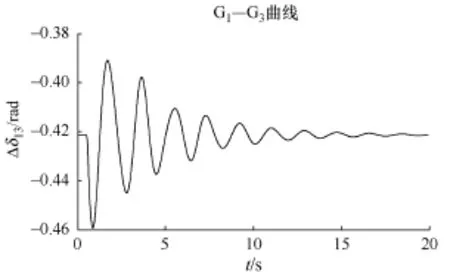
图6 计及随机性的实时修正控制功角图

3.2 某地区电网算例

以某地区电网进行仿真，该地区电网模型中含有发电机64台，节点294个和线路共计628条。通过频域分析发现，该系统存在63个低频振荡模式，由运行经验可知，其中 FJ模态对系统影响较为严重，通过模式辨识，可以确定 FJ模态的频率为0.53Hz。

通过计算FJ模态的左右特征向量，可以得出该模态的相关发电机分别为B23和B45。在0.5s时在节点Jp12处施加一个扰动，系统发生模式为FJ的低频振荡，系统仿真结果如下。

图7所示的曲线分别为3种情况下节点B23和B45处发电机间的功角差，仿真时间为20s。从图7可以看到，该系统在受到干扰后发生了模式为FJ的低频振荡，在考虑负荷以及风机随机性的情况下，如果不采取控制措施，系统振荡就会很快发散，危害系统的安全运行；如果采取常规的确定性控制措施，系统发散的速度就会减缓，但仍然不能有效的抑制该模态；通过采取实时修正控制的情况，低频振荡逐渐平息，系统进入到稳定状态，符合预期的效果。

综上可知，在确定性的场景下，原有的修正控制能及时抑制电力系统的低频振荡。在考虑系统随机性的情况下，原有控制失效了，如果在这种情况下采取实时修正控制措施，就能够及时平息系统的低频振荡，这验证了所提出措施的有效性。

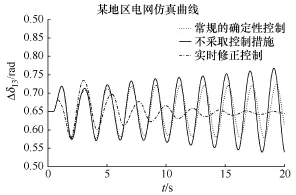
图7 某地区电网仿真图

4 结论

本文在概率特征根的基础上提出了阻尼比灵敏度指标，结合半不变量法，求得阻尼比的概率分布，确定边界阻尼比系数，以制定最优的实时修正控制措施，包括控制选址和控制量的确定。算例表明，在系统发生低频振荡后，受到随机性的影响，常规的修正控制措施不能有效的平息系统的低频振荡，而采用实时修正控制后系统低频振荡很快平息，验证了考虑随机性的情况下实时修正控制的有效性。

[1]田立峰,李成鑫,刘俊勇.电网低频振荡在线可视化监视的理论和实现[J].电力自动化设备,2010,30(5):28-33.

[2]郑伟,鲍颜红,彭慧敏,等.基于受扰轨迹模式分析的动态稳定辅助决策[J].电力系统保护与控制,2013(4):79-83.

[3]陈磊,陈亦平,戴远航,等.基于 WAMS的南方电网低频振荡调度应对策略[J].南方电网技术,2013(4):12-18.

[4]李安娜,吴熙,蒋平,等.基于形态滤波和 Prony算法的低频振荡模式辨识的研究[J].电力系统保护与控制,2015(3):137-142.

[5]Pourbeik P.Gibbard M J.Simultaneous coordination of power system stabilizers and FACTS device stabilizers in a multi machine power system for enhancing dynamic performance[J].Power Systems IEEE Transactions,1998,13(2).

[6]陈中.电力系统小干扰稳定实时控制[J].电力自动化设备,2012,32(3):42-46.

[7]周崇雯,罗骏,汪芳宗,等.基于不完全S变换的低频振荡可视化实时监测方法[J].电力系统保护与控制,2015(24):63-68.

[8]谢志棠,宗秀红,钟志勇,等.计及 FACTS装置的概率特征根分析[J].电力自动化设备,2004,24(8):13-17.

[9]Rueda J L,Colome D G.Probabilistic performance indexes for smallsignal stability enhancement in weak wind-hydro-thermal power systems[J].IET Generation,Transmission and Distribution,2009,3(8):733-747.

[10]Krause G.From turbine toand spin-off products[M].India:wind farms:technical requirements In Tech,2011.

[11]周明,元博,张小平,等.基于SDE的含风电电力系统随机小干扰稳定分析[J].中国电机工程学报,2014(10):1575-1582.

[12]王克文,谢志棠,史述红,等.基于概率特征根分析的电力系统稳定器参数设计[J].电力系统自动化,2001,25(11):20-23.

[13]Zhang P,Lee S T.Probabilistic load flow computationusing the method of combined cumulants and Gram-Charlier expansion[J].IEEE Transactions on Power Systems,2004,19(1):676-682.

[14]石东源,蔡德福,陈金富,等.计及输入变量相关性的半不变量法概率潮流计算[J].中国电机工程学报,2012,32(28):104-113.

[15]苏展,徐谦,孙黎滢,等.含 DFIG的电力系统随机建模及小干扰随机稳定分析[J].电网技术,2015,39(9):2404-2410.

[16]岳昊.考虑并网风电随机波动的电力系统小干扰概率稳定研究[D].北京:华北电力大学,2014.

[17]门锟,吴超,涂亮,等.互联电网功率振荡辨识方法应用研究[J].深圳大学学报(理工版),2014(3):299-306.

[18]赵红生,刘源,陈伟彪,等.互联电力系统联络线功率波动机理及其扰动概率分析[J].电力系统保护与控制,2015,43(14):1-9.

Real Time Correction Control of Low Frequency Oscillation in Power System with Randomness

Zong Pengpeng Wang Peixiu Yan Jihong Yang Qinchen Wu Jianchao
(School of Electrical Engineering,Southeast University,Nanjing 210096)

The main research of this paper is the real-time stability of the system with low frequency oscillation in power system.This paper analyzes the change of the probability distribution of the damping ratio in the case of the randomness,and the calculation method is derived.Based on probability damping ratio and damping ratio sensitivity,control measures have been quantified,in order to determining the optimal control measures,which include control location and amount.The simulation was carried out in two area four machine system,in which the validity of the real time correction control is verified.The method proposed in this paper can effectively suppress the oscillation mode of the system,in which the randomness is considered compared with traditional control measures.

cumulant;probability analysis;low frequency oscillation;characteristic root sensitivity

宗鹏鹏（1992-），男，硕士研究生，研究方向为电网低频振荡分析、电网运行控制。

国家自然科学基金项目（51277029）