液体罐装车罐体结构稳定性研究

刘耀邦，程 章

（1.安徽交通职业技术学院 汽车与机械工程系，安徽 合肥 230051；2.合肥工业大学 汽车与交通工程学院，安徽 合肥 230009）

液体罐装车罐体结构稳定性研究

刘耀邦1,2，程 章1

（1.安徽交通职业技术学院 汽车与机械工程系，安徽 合肥 230051；2.合肥工业大学 汽车与交通工程学院，安徽 合肥 230009）

液体罐式车在运输行业中应用极为广泛，相对较其他运输车辆，研究基于液罐车罐体部分的气液两相流固耦合现象和其工作状态下的外界激励产生的振动，本文以相流模型作为理论基础，建立该液罐车的整车UG模型和有限元模型，通过液罐车的静态结构分析及固有频率与随机振动频率的研究，能够有效避免共振而引起的结构局部变形或结构破坏现象.

液罐车；相流模型；有限元分析；模态分析；稳定性

1 引言

罐式汽车[1-3]是指装有罐状容器的完成特定作业任务的专用车辆和专用汽车列车[4]，用于运输液体、气体或粉粒或粉末状物质.20世纪50年代起，我国开始进行罐式专用车制造.如今，罐式运输车基本实现多功能化、大容量化及自动化.本文的研究对象——半挂式液体罐装车实物图如图1所示.其罐体部分与车架部分刚性连接.罐体部分为封闭的伴有筒体、封头、防浪板及管道的罐式容器.

本文重点考虑特殊工况下，液体产生的瞬态动载荷可能产生的液罐车结构失效，国内外越来越多的学者投入到固液耦合振动方面的研究，俄罗斯和美国率先取得研究成果，1953年，Niordson F.I和V.N.Pi1ipchuk等人对储液容器振动问题进行的研究[5]，并将搭建模型进行研究[6].20世纪80年代，以居荣初为首的液固耦合问题研究成果应用于实际抗震分析中[7].90年代，王世忠[8]等人更是取得突破性成果.

图1 液罐车实物结构图

2 欧拉多相流模型

气液两相流模型如图2所示[9]，从图2可见，气体与液体之间存在明显的界面.

图2 气液两相流自由液面图

当各相质量、动量传输方程均不同时，引入欧拉多相流模型[10]，其方程为：

其中：Ta=c12(ø2-ø1)

多相流模型质量连续方程：

多相流模型动量传输方程：

其中：ρ：混合流体密度；U：平均速度；ø：实际含气率；p：混合流体压强.

3 罐体模型建立

液体罐式运输车常运输易燃易挥发液体，本文的液罐车用来运输环庚烷，环庚烷为无色油状液体，沸点118.5℃，相对密度0.81（20℃），闪点6℃，燃点极低，化学特性不稳定，其蒸气与空气混合时遇热源和明火燃烧和爆炸的可能性极大.所以液罐车在运输过程中必须具有更高的可靠性，以防出现问题.

3.1 液体罐式运输车UG模型

液罐车主要由罐体、防护装置、管道系统、人孔、行走系统、灭火器、支撑装置、车架、牵引装置、扶梯等组成，在不同的工作条件下，应力状态是不同的.由于液罐车工作情况的特殊性，所以要求车架、罐体等主要部件应该具有较高的强度、刚度和形状稳定性，以承受复杂的各种载荷而呈现正常工作状态，并且要求它的质量尽可能小.基于此，对罐车模型进行各工况的结构静力分析，找出结构应力集中及较大位置.

该液体罐式运输车的参数如表1所示：

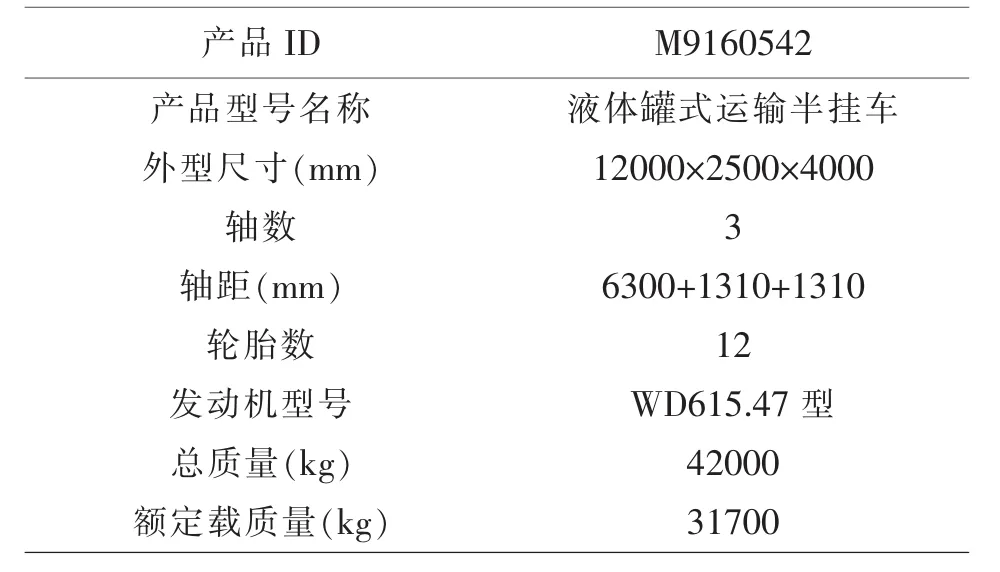
表1 液罐车参数

图3 罐式运输半挂车的UG模型图

根据液罐车的二维CAXA图纸并参考液罐车实车结构，进行该易燃液体罐式运输半挂车三维建模工作，得到如图3所示的易燃液体罐式运输半挂车UG三维模型.

3.2 有限元模型建立

根据罐体结构力学原理，对罐式运输半挂车的罐体结构进行简化，忽略结构受力较小部件，如行走平台、人孔、灭火器、防护装置、扶梯等；对于起着支撑作用的结构，以约束来进行处理.建立罐车有限元模型，经过模型的简化、几何模型的建立、建模的单元的选择、网格划分等，液罐车有限元模型如图4所示.最后得到的结构有限元模型共341516个节点，345042个单元.

图4 罐式运输车的有限元模型

4 液罐车模态分析

固有频率是研究动态物体特征的重要参数，其数值与研究对象的结构、形状及材料属性有关，因固有频率与振动状态的强弱没有关联，但是外界的激振干扰频率可能影响到液罐车的结构建模及产生共振造成的结构破坏，进行液罐车结构的模态分析，是为了明确液罐车的结构模型以及不同模态时液罐车的固有频率[12]，便于研究者了解外界的激振干扰频率到液罐车的结构建模的影响，并考虑共振现象存在与否.

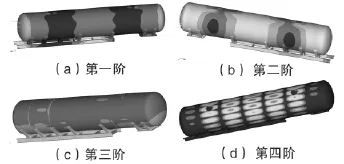
图5 各阶模态云图

很显然，液罐车是一个多自由度系统的运动体，其自身激励难免造成车体振动，外界激励也会影响到振动研究.比如路况的不同，会出现不同的外界振动激励，尤其要注意随机振动频率等同于固有频率而出现的共振.当液罐车工作时，其发动机气体燃烧出现的压力变化和活塞工作的惯性产生的振动是液罐车自身激励的主要来源[13]，这些自身因素和外界激励的频率与液罐车某一阶对应固有频率值接近时，就会产生共振，结果轻则引起液罐车的局部结构变形，重则会造成液罐车的总成结构破坏.

罐车固有振型有罐车的整体振动和以罐车一个或几个部分振动为主的局部振动两大类.本文重点研究中主要考虑局部振动模态，局部振动模态图如图5所示.

前六阶次振型的结构固有频率如表2所示，可见，液罐车第一阶模态结构的固有频率为50.46Hz，远远高于外界激励频率，从液罐车的前六阶结构固有频率可以看出半挂液罐车整体结构振型平稳.

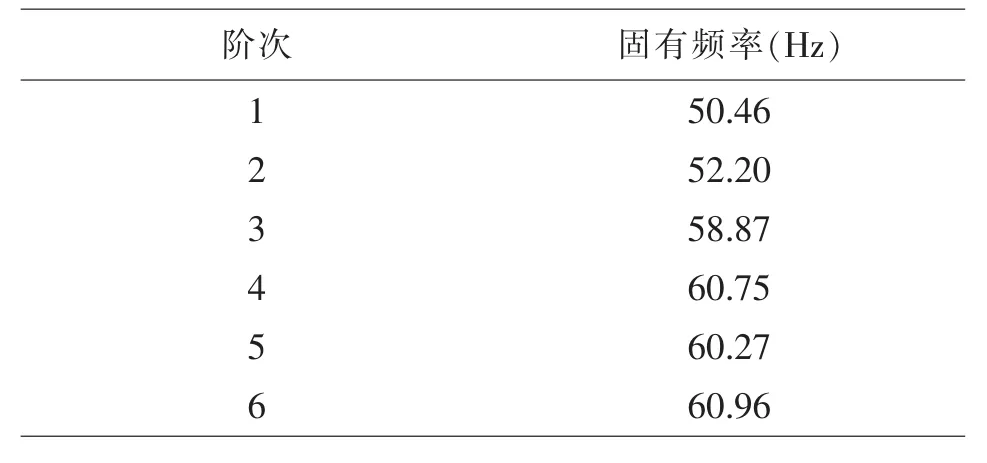
表2 前六阶次振型结构固有频率

液罐车工作时主要激振频率为路面不平度引起的激振频率，值域[1Hz,20Hz]，其次为发动机工作引起的频率范围较宽的简谐激励.根据频率计算结果以及液罐车模态分析结果可知，液罐车一阶模态频率为50.46Hz，不仅仅高于路面激励频率，也高于发动机工作时气体燃烧出现的压力变化和活塞工作的惯性产生振动的固有颇率，而且振型平稳，可以确定外界频率的激励对液罐车的整车各阶模型的影响可以忽略.

5 结论

根据半挂液罐车的自由模态分析，得到液罐车的固有频率及前面六阶的振型，根据分析，可知液罐车整体结构的固有频率值较高，集中在[50.46Hz,60.96Hz]值域范围，外界激振频率对其影响可以忽略不计，排除了液罐车因为共振而导致的局部结构变形及破坏，该研究为今后的液罐车瞬态响应分析提供了可靠的理论依据和模型平台.

〔1〕明平顺.汽车运输专用车辆车[M].北京:人民交通出版,1997.1-3,66-78.

〔2〕冯晋祥.专用汽车设计[M].北京：人民交通出版社,2007.193-240.

〔3〕严大凡.油气储运工程[M].北京：中国石化出版社,2003.222-226.

〔4〕端木凡峰.液罐车罐体有限元仿真分析及研究[D].新疆农业大学,2010.

〔5〕Niordson F.I.Vibrations of a cylindrical tube containing flowing fluid[J].Kungliga Tekniska Hogskolans Handlingar（Stockhohm).1953,73:40-48.

〔6〕V.N.Pilipchuk,R.A.Ibrahim.The Dynamic of nonlinear systemSimulating liquid sloshing impact inmoving structures[J].Journal of Sound and vibration,1997,205(5):593-615.

〔7〕居荣初，曾心传.弹性结构与液体的耦联振动理论[M].地震出版社,1983.201-207.

〔8〕王世忠，王茹.三维管道固液耦合振动分析[J].哈尔滨工业大学学报,1992（04）.

〔9〕林宗虎.多相流体力学及其工程应用[J].自然杂志,2006（08）:47-51.

〔10〕蒙伟安,穆塔里夫·阿赫迈德.T型管流场混合多相流与欧拉多相流模型的数值研究[J].机械设计与制造,2012(02):26-31.

〔11〕陈玉杰.客车车身骨架有限元建模及优化分析[D].合肥工业大学,2007.

〔12〕王玉超,王力,宋俊.利用CWELD和RBE2模拟焊点模态及刚度分析[J].现代制造工程,2009 (04):85-89.

〔13〕谢小平,韩旭,吴长德,雷飞.基于PolyMAX方法的某轿车白车身实验模态分析[J].汽车工程, 2009(5):440-443,447.

TH48

A

1673-260X（2017）01-0024-03

2016-10-23

安徽省2014年省级质量工程：工程机械运用与维护专业（群）教学团队（2014jxtd084）