《常量与变量》课堂实录（节选）

《常量与变量》课堂实录（节选）

科 目 数 学

执教者李 玲/湖北省武汉市经济技术开发区第一初级中学教师、高级教师

点评者翟立安/上海市数学特级教师

教学目标

1.在具体情境中领悟常量与变量的含义，能分清实例中的常量与变量。

2.用运动的眼光观察生活，关注一个量随另一个量变化而变化的现象。

3.感受“万物皆变”，保持对世界的敏感和好奇，感知规律的普遍存在。

制造一次纠结

师：我这里有一个圆柱体的水槽，可以求它的容积吗？

生：可以，V=Sh（S是水槽的底面积，h是水槽的高度）。

师：现在向水槽中注水，水槽里发生了什么变化？

生：水面不断上升，水越来越多，……

师：在注水的过程中，水的体积可以求吗？（学生开始“纠结”）

生：能，因为水槽中的水是圆柱体，用V=Sh就可以计算了。

生：不能，注水的过程中，水面高度不断上升，体积逐渐变大，不能求。

师：观点不同，但并不矛盾，只是所站的角度不同，看问题的眼光不同。

用运动变化的眼光看，注水的过程，水面的高度不断上升，体积也随着变化。

用静态的眼光看，上升中的每个时刻都可以测量一个高，有一个确定的体积。

小结：我们习惯于计算一个杯子的容积，计算一次运动的路程，计算一次购物的总金额，我们总在追求计算一个结果。然而，当用运动的眼光去观察时，我们看到的就是量与量之间的联系，或者说是规律。

板书：

【意图：制造一次“纠结”，经历动与静的冲突。】

点评：

这个引入比较妙！一是因为它是生活中常见的情景；二是因为它是从静态很自然地走向动态；三是因为蕴含了本课的关键要素；四是因为一静一动，引发了学生的比较与思考，产生了“纠结”引发了学生探究的兴趣。

关注一类现象

师：在一个变化过程中，数值发生变化的量叫变量，保持不变的量叫常量。

当S一定时，V随h的变化而变化，其中，S是常量，h和V是变量。

当h取一个值时，V有一个值与之对应。

（用几何画板动态演示）

点评：

数学学习经常要经历“具象、表象、抽象”这三个环节，有时是具体的形象在前，再到表象然后抽象；也可以先给出抽象的概念，再用具体的形象来解释或演示，让学生多感性地感悟。这里的几何画板演示，就起到了在出示概念后用学生对具象的感悟对概念的理解。

师：生活中广泛存在着一种现象：一个量随另一个量变化而变化，看下面例子，指出其中的变量和常量。

（1）下表反映了一家的奶茶店的销售情况。

销量X(杯) 1 2 3 4 5 6 7 ……销售额Y(元) 6 12 18 24 30 36 42 ……

变量_____，常量____；____随____的变化而变化。

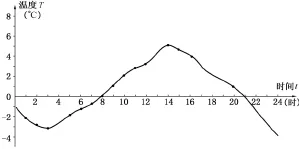
（2）下图表示了一天之中，____随____的变化而变化，变量____，常量____。

（3）以速度v0(m/s)向上抛一个小球，小球的高度h(m)与小球的运动时间t(s)之间的关系式为：h=v0t-4.9t2。在这一变化过程中，____随____的变化而变化，变量____，常量____。

（学生产生疑惑：两个人抛球，v0或许不相同，v0是常量还是变量？）

师：当理解模糊，产生疑问时，请“回到定义上去”。

生：不同的人抛球，表示不同的变化过程中，就好比（1）中我家的奶茶6元一杯，你家的奶茶8元一杯，而6和8都是各自变化过程中的常量。

（学生关注到了定义中的“在一个变化过程中”的前提，并用更容易理解的例子来打比方解释，领悟到字母不一定就表示变量，为学生点赞。）

点评：

学生所以能够有如此精彩的回答，是因为老师的启发到位，“请回到定义”给学生思考指引了方向。数学概念教学要紧扣概念中的条件与结论，甚至要逐字逐句地分析概念的内涵，尤其是对关键词的重点思辨。

小结：两个变量之间的关系的表达形式可以是（1）中的表格，可以是（2）中的图像，可以是（3）中的解析式，也可以用语言来描述。

点评：

选择的三个生活中的现象，很典型，也比较全面，为后续学习函数打下良好的伏笔。

【意图：关注一类现象，聚焦概念的理解。】

保持一份敏感

师：“万物皆变”——行星在宇宙中的位置随时间而变化，气温随海拔而变化，树高随树龄而变化……在你周围的事物中，这种一个量随另一个量的变化而变化的现象大量存在，请你继续举例，并指出其中的常量和变量。

生：加油过程中，油费随汽油数量的变化而变化；股价随时间的变化而变化；心电图人体的生物电波随时间的变化而变化；圆面积随半径的变化而变化；匀速运动中，路程随时间的变化而变化……

（学生又回到往圆柱体水槽中注水的例子，水的压强随水的高度的变化而变化；水的重力随水的高度变化而变化。)

【意图：保持一份敏感,唤醒对世界的好奇。】

点评：

让学生举例，是判断学生是否真正理解概念的一种方法，能够正确举一反三者，是理解概念者，只要不是机械模仿。

完成一次探索

师：一种手机卡有两种收费方式。（接听免费）

A套餐：月租费22元，拨打每分0.2元；

B套餐：无月租费，拨打每分0.4元。

请你为客户制作一份选择方案。

（学生独立思考以后展开讨论）

生1：B套餐合算，因为不用交月租费。

生2：我不同意，如果打200分钟，B套餐收80元，A套餐只要62元。

我认为有时候A套餐划算，有时候B套餐划算

生3：费用跟拨打的时间有关，时间不一样费用就不一样。

生4：费用随拨打时间的变化而变化，可以设拨打时间为x分。

0.2x+22=0.4x，x=110

当每月拨打时间≤110分时，选B套餐；

当每月拨打时间≥110分时，选A套餐。

作业：温度随海拔高度的变化而变化，具体关系如下：T=a-0.65h。

a表示海平面处的气温摄氏度，h表示海拔高度的百米数，T表示在h高度处的温度。仅仅使用温度计，能估算一座较高的山的高度吗？

【意图：完成一次探索，认识研究的必要。】

点评：

探索手机套餐问题，用来说明研究的必要性，最好能与本节课所学“常量”“变量”紧密相连。例如：师生合作分析时要注意突出不同套餐是不同的“一个变化过程”，要分析出常量、变量。当学生产生了方程“0.2x+22=0.4x”，老师要追问“如何想到利用方程来解决的？”因为这是两个变化过程中寻找一个费用相等的时间常量。

讲述一段史实

师：400年前，德国天文学家开普勒发现了行星运行的三大定律，破译了天体运动的运行规律。人们按照开普勒定律观测天王星时，发现它的实际运行轨道出现了偏差，猜想一下会是什么原因造成的？

生：因为另一个量的变化而变化。

点评：

这里学生回答含糊，到底是那个量的变化引起了另一个量的变化？教师要追问到让几乎让所有学生都明白的地步，要生发出集体思维的“共振”，让学习在每个学生身上真正地发生！

师：的确如此，根据天王星轨道的偏差推算出，并成功地观测到了海王星，这颗利用掌握的规律进行数学运算发现的行星，被称为“笔尖下的星球”。在此基础上牛顿发现了更为普适的万有引力定律，把地面上物体运动的规律和天体运动的规律统一起来，我们也不禁惊叹，浩瀚的银河系，共同遵循着同一条规律有序地运动变化。

常量变量带我们走进了真实的运动变化的生活，希望同学们永远保持对世界的惊讶与好奇，用数学的眼光和方法去解开更多的规律，探索更多的奥秘。

点评：

整个教学设计，非常自然流畅，流淌在学生的最近发展区，又引发学生合作探讨的兴趣，体现了教师较高的数学素养和教学设计的独具匠心。

【意图】讲述一段史实，展望课题远景。

设计思路

李玲/文

常量和变量是函数的萌芽，本节课是为函数的学习埋下一颗种子。我设计了五个问题，但答案得由学生给出。

问题一制造了一次“纠结”，“纠结”中学生经历了动与静的冲突。从静态的常量数学到动态的变量数学，学生看问题的角度和眼光、思维方式都将发生深刻的变化。

问题二动态直观地让学生关注到一种现象：一个量随另一个量变化而变化，这是本节课的核心。一方面常量变量是在这一现象中定义的；另一方面现象的本质就是函数，举例过程中，有解析式、表格、图像，让学生提前感知了函数表达的三种形式，为后续学习作铺垫。

问题三请学生大量举例，加深对概念理解的同时希望他们保持对世界的关注和好奇。孩子小时候都特别喜欢问“为什么”，随着年龄的增长，问题就变少了，是问题都解决了？更可能是司空见惯了，这种麻木要引起重视和警醒。

问题四在真实的问题情境中定方案、做决策，学生是用方程解决的问题，方程思想是动中求静，研究运动中的等量关系，和函数思想有着密切的联系。问题的解决让学生进一步认识到生活是运动变化的，变化的问题是有办法去研究的。

问题五讲述了海王星的发现过程，无论是科学领域，还是人类社会的发展都依赖于对规律的逐步揭晓和利用，惊奇和震撼让对学生对后续的学习满怀期待。

义务教育阶段的数学课讲授的是最基础的数学知识，是人类历经几千年的智慧结晶。当我欣喜地、精确地与学生分享我的所知、所思、所得时，他们却未必能精确地接受，更谈不上欣喜。于是我开始研究我的学生，这个过程让我充满了“共情”的能力，我也在学生和学科之间找到了一条“浪漫”的路径：用合适的问题开启学生的思考，学生自己悟到的才真正属于自己。

知识本身固然是知识，在解决问题的过程中所积累下的活动性经验又何尝不是知识呢？它是学生面对未知，走向未来的知识和力量。