培养问题意识 提升思维能力

培养问题意识 提升思维能力

■陈德前

《义务教育数学课程标准（2011年版）》（以下简称新课标）在总目标中指出：“通过义务教育阶段的数学学习，学生能体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力。”我们知道，对于分析和解决问题，其中已知和未知都是明确的，只是需要利用已有的概念、性质、定理、公式、模型，运用恰当的思路和方法得到问题的答案即可；而对于发现和提出问题，其中的已知和未知都是不明确的，所以其难度很大，对思维的要求更高。正如爱因斯坦曾强调的：“发现问题和系统阐述问题可能要比得到解答更为重要。解答可能仅仅是数学或实验技能问题，而提出新问题、新的可能性，从新的角度去考虑老问题，则要求创造性的想象，这标志着科学的真正进步。”因此，新课标把原来的增强分析问题和解决问题的能力，发展为现在的增强发现和提出问题的能力、分析和解决问题的能力。可见，在新课标培养学生创新精神和实践能力的总体目标下，培养学生的问题意识，尤其是发现和提出问题的意识，提升学生的思维能力就显得非常重要。那么，如何在数学教学中落实这个要求呢？下面谈一点个人的浅见。

一、精细研读教材，挖掘培养问题意识的素材

我们知道，学生问题意识的培养是蕴含在具体的素材之中的，在课堂教学中要培养学生的问题意识，引发学生的思维，就必须提供必备的素材。那么素材从哪里来？我们认为，教材是最重要的来源。在我们使用的各种版本的教材中，都隐含着丰富的培养学生问题意识的优秀素材。我们必须通过精细研读教材、深刻理解教材，才能将教材中隐含的培养学生问题意识的素材挖掘出来，再根据本班学生的具体情况，经过教师的创造性工作，设计出有效培养学生问题意识、提升学生思维能力的教学方案。苏科版新版初中数学教科书在编写中十分重视学生问题意识的培养，通过“做一做”“数学实验室”“数学活动”等栏目，引导学生通过实验操作，观察思维，归纳猜想，去发现问题、提出问题，进而分析问题和解决问题。

案例1：苏科版初中数学教材七（上）6.1线段、射线、直线（1）。

通过研读教材P146-148，我们不难发现，在这部分的教学内容中，有许多培养学生问题意识的好素材：（1）在连接两点之间的多条线中，哪一条最近？除了这些线，还有没有更短的路？如果有，是否存在最短的？如何修出这条路？（2）怎样规定两点之间的距离？这样的规定合理吗？（3）两点间的距离是不是就是两点间的线段？如果不是，它们之间有什么关系？（4）怎样从线段出发，得到射线、直线的概念？（5）理解射线的定义要抓住哪些要素？怎样的两条射线才是同一射线？（6）线段、射线、直线之间有什么联系？又有哪些区别？（7）怎样科学地进行线段的计数？如何推广到一般情况？（8）为什么两点就可以确定一条直线？它在生活中有哪些应用？等等。只有经过精细研读，深刻思考，教师在教学中才能充分利用学生已有的线段、射线、直线的知识和经验，以挖掘出的培养问题意识的素材为载体，引导学生经过自己的思维，去发现问题、提出问题，进而分析问题和解决问题，相机地培养学生的问题意识，有效地进行知识建构。

二、针对具体学情，把握培养问题意识的梯度

问题意识的培养是一个复杂的系统工程，根据年级的不同、班级的不同、城乡的不同，这个工程的具体要求、序时进度也不尽相同，需要针对学情，循序渐进，拾级而上。只有了解学生、研究学生、全面掌握学情，才能把握培养学生问题意识的梯度。因此，要有效培养学生的问题意识，教师就应当对学生的知识基础、已有经验等做具体而深入的分析，这是有效设计教学预案、高效实施课堂教学的坚实基础。

案例2：苏科版初中数学教材七（下）12.2证明（1）中“做一做”。

（2）换几个数再试试，你发现了什么？

关于这个活动，学生已经具备的知识和经验主要有：（1）有理数的运算；（2）代数式求值的方法与技巧；（3）乘法公式的双向运用；（4）非负数的性质；等等。如何利用这个素材来培养学生的问题意识呢？学情不同，实施的策略也应该有所不同。对于基础比较薄弱，经验迁移能力较弱的班级，可以先设计出如下表格，来引导学生思考，发现结论：

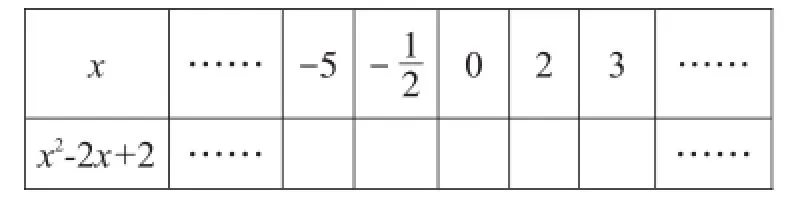
然后，请学生观察表中运算的结果，问他们有什么发现，请他们把发现写下来。接下来，再提出问题启发学生：换几个数再试试，刚才的发现还成立吗？你能试着说明理由吗？对于基础好，思维能力强的班级可以直接在学生计算的基础上，提出问题：结合你的计算结果，你能发现哪些结论？说明你的结论的正确性。

面对同一个代数式，不同层次的学生从不同的角度观察、思考，会探索出不同的结论，如：（1）2-2m+m2的值一定是偶数；（2）2-2m+m2的值是正数；（3）2-2m+m2的值大于1。这些结论有的正确，有的错误，要求学生都必须通过说理来作出判断，并归纳出解决这类问题的一般性方法，即要说明一个代数式取值范围的正确性，将代数式进行变形是最常用的方法。在此基础上，对于学优生，还可以用代数式的变形为抓手，抓住前后知识的联系，充分利用学生的知识最近发展区，引导学生拾级而上，不断地发现和提出问题。如：（1）这个代数式有最大（小）值吗？何时取得最大（小）值？（2）x为何值时，代数式的值随x的增大而增大（减小）？等等。同时，帮助学生学会通过有条理地思维来分析和解决问题，不断积累初步的发现和提出、分析、解决问题的基本活动经验，从而达到预期的教学目标。

三、创设多元情境，提供培养问题意识的契机

问题的发现和提出必须有好的情境，创设出好的情境是开展有效教学、高效教学的前提，这是因为好的情境具有引领学生思维、激发学习欲望的作用。那么，怎样的情境才算是好的情境呢？湖北省教科院的裴光亚先生对此作了精辟的论述：愤、悱是对“情境”的恰当描述。愤，就是让学生想弄明白但又感到困难；悱，就是学生想说出来但又说不明白。好的情境不仅仅只是“问题”，在它的背后更要有内在需求，能激发起学生主动探究的愿望。江苏省教研室董林伟先生把好的数学情境归纳为三个特征：（1）学生熟悉的；（2）简明的；（3）必然引向数学本质的。我们在数学教学中，要依据这些情境设计的原则，精心设置多元情境，为学生提供培养问题意识的契机。

案例3：见本期栏目中的《苏·科版七（下）“证明（1）”教学案例》。

这节课注重对问题情境的精心设计。首先，教师给出了两幅图片，图片中有两个等大的圆，一个是大圆内的小同心圆，一个是小圆外的大同心圆。教师先让学生观察后给出结论，再通过平移两个等圆使其重合，学生发现观察得到的结论不正确，“眼见不一定为实”。它满足了有效问题情境应具有的三个特征，既是学生熟悉的，又是十分简明的。学生在探讨结论正确性的过程中，认识到数学的本质——说理的必要性，教师便自然而然地导入了新课。接着，在探索活动中，又设置多元活动情境，教师引导学生分别从生活问题（活动1）、代数问题（活动2）、图形剪拼问题（活动3）、图形旋转问题（活动4）等不同层面进行探究。教师不是将结论直接告诉学生，而是不断创设思维情境，提供机会让学生去动手操作、观察思考，引领学生来发现和提出问题，并通过小组和全班交流的方式来分析和解决问题，让学生经历问题的发现、提出、分析和解决的完整过程，引领学生的思维向纵深发展，不断积累基本活动经验。在活动1中，教师以“曲径”面积的计算为情境，在学生的思维“最近发展区”内提出问题。教师给学生提问的示范，使他们领悟了发现和提出问题的艺术；学生通过合情推理多角度地得到同一结论，再通过演绎推理来说理。活动2以计算代数式的值为情境，让学生借助表格来发现问题（结论），提出问题（结论），并应用已有的知识和经验来进行分析，体会出利用取特殊值是可以说明结论的，但不可以说明某个结论就一定正确；让学生进一步感悟出利用演绎推理来说理的必要性，尝试了步步有据地进行说理。活动3以图形剪拼问题为情境，让学生尝试提出问题，并通过计算图形的面积说明由8×8的正方形剪拼为13×5的长方形的不可能性。活动4则借助多次操作，引导学生通过合情推理来判断PE与PF的大小关系，再利用操作中不同的特殊位置，通过演绎推理来多角度说明PE=PF的正确性，进一步引导学生用多种方法来表征说理的过程，提升演绎推理的能力。其次，教师布置的课堂练习，更让学生完整经历了用合情推理发现并提出问题，从特殊到一般探索归纳结论，再用演绎推理证明结论的过程。最后，教师又以问题情境进行课堂小结，让学生谈对说理的感受，进一步感受说理的重要性；教师归纳出说理的常用方法，不断帮助学生积累说理的基本经验，提升学生的说理水平，并让学生提出新的问题，既进一步提供了培养问题意识的契机，又为后面的学习做了铺垫。

四、注重积极评价，提升培养问题意识的情感

新课标指出：“对学生数学学习的评价，既要关注学生知识与技能的理解和掌握，更要关注他们情感与态度的形成与发展；既要关注学生数学学习的结果，更要关注他们在学习过程中的变化和发展。评价的手段和形式应多样化。”由于发现问题和提出问题的难度很大，对思维的要求更高，因此，我们要根据新课标的评价理念，在评价的有效性方面进行精心思考，大胆探索课堂的多元评价方式，发挥积极评价在培养学生问题意识中的情感作用。课堂上，教师不仅要关注学生基础知识和基本技能的掌握情况，更要关注学生能否用数学的眼光发现问题，用数学的语言提出问题，用数学的方法分析问题，用数学的范式解决问题。教师要关注每个学生特别是学困生的学习过程，采用多元评价，及时鼓励学生，如：口头评价中的“你的回答真棒”“问题表述得很规范”“这真是个好问题”“讲得太精彩了”“问题提得很有特色”，等等；体态评价中的竖起大拇指、OK手形、掌声，等等。要充分发挥学生之间评价的作用。在课堂小结环节，教师要组织学生对自主探索、合作交流、小组汇报、问题讨论等环节中自己的表现和同学的表现进行评价，通过学生的自评、互评，小组评，全班评，使评价的结果相对合理。总之，要通过形式多样、丰富多彩的积极评价，不断提升学生情感，使学生问题意识的培养真正落到实处。