|x|α在一类结点组的有理插值

蒋银停，赵 易，许江海

(杭州电子科技大学理学院，浙江 杭州 310018)

|x|α在一类结点组的有理插值

蒋银停，赵 易，许江海

(杭州电子科技大学理学院，浙江 杭州 310018)

有理插值；Newman-α型有理算子；稠密；逼近阶

0 引 言

1918年，文献[1]证明了在等距结点处的关于Lagrange插值多项式序列的一个经典的结果，除了端点及零点，该插值多项式序列在任何其它点处都发散.1964年，文献[2]发现|x|的有理插值的逼近阶远优于其Lagrange插值逼近.之后，有不少研究者考虑了在不同类型结点组的Newman型插值.如文献[3]与文献[4]分别给出了当结点组取作Chebyshev结点及调整的Chebyshev结点时的相应的逼近阶.

比较文献[3]与文献[4]的结论，并从文献[4]中得到灵感，2003年，文献[5]的作者构造了一类新的结点组，并计算了函数|x|在此结点组处的有理插值逼近阶.

以上问题均关于函数|x|展开，讨论其在不同结点组处的多项式插值与有理插值；另一方向的推广，是对函数|x|的探究.2000年，文献[6]把Bernstein的结果推广到更一般的情况，即当0<α≤1时，|x|α的Lagrange插值多项式有类似的发散性.

本文研究|x|α的有理插值问题，并讨论其逼近度.可以证明，在选取适当插值结点的情况下，其逼近效果较好.同时，本文结论也包含了之前的一系列结果.

1 rn,α(X;x)对|x|α的有理逼近

定义Newman-α型有理算子如下：

本文采用文献[5]中的插值结点，具体构造如下：

当n为奇数时，即n=2m-1，记

x1=1/m2,x2=2/m2,…,xm-1=(m-1)/m2,xm=1/m,…,x2m-1=1.

(1)

当n为偶数时，即n=2m，记

x1=1/(m+1)2,…,xm-1=m/(m+1)2,xm+1=1/(m+1),…,x2m=m/(m+1).

(2)

本文主要针对式(1)和式(2)的结点组，讨论rn,α(X;x)对|x|α的有理逼近.

证明 首先取x∈(j/m2,(j+1)/m2),j=1,2,…,m-1.有

由于x≥0，1-x≤e-x，

上述证明只获得在区间[1/m2,1/m]时的结论，同理可证在区间[1/m,1]上，

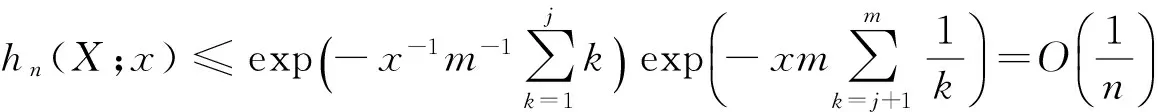
引理即证.

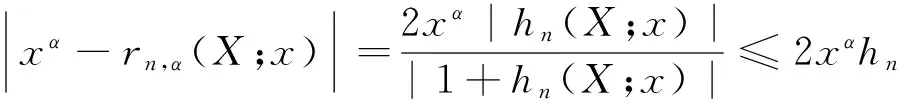
其中

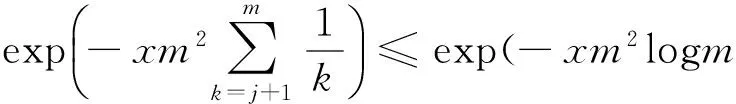
情形2 当x∈[1/m2,1/m]，j/m2≤x≤(j+1)/m2，j=1,2…,m-1.当n充分大时

并且

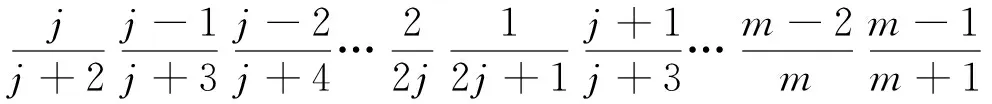
其中，j+2≥3,j+3≥4,…2j≥j+1,2j+1≥j+2.

故

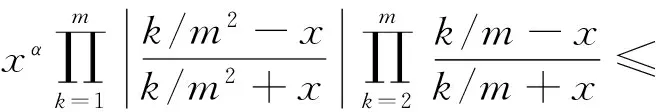
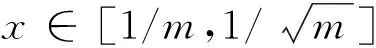
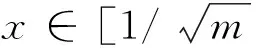
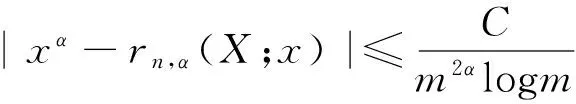
最后，需要证明上述的逼近阶是不可改善的，令x*=x*(n)=α/(m2logm)，x*∈(0,1/m2)，仍由引理，当n充分大时，有

(3)

由此可得

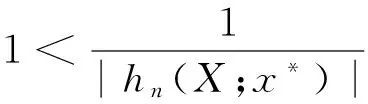
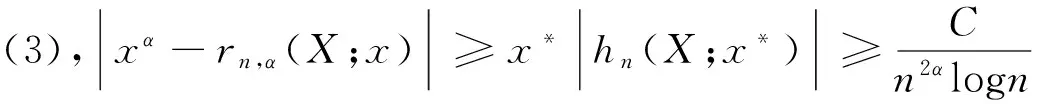
2 结束语

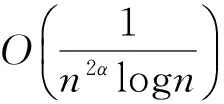
[1]BERNSTEINS.Quelquesremarquessurlinterpolation[J].MathematischeAnnalen，1918，79(1):1-12.

[2]NEWMANDJ.Rationalapproximationto|x|[J].Michigan Mathematical Journal，1964，11(1):11-14.

[3]BRUTMAN L，PASSOW E.Rational interpolation to |x| at the Chebyshev node[J].Bulletin of the Australian Mathematical Society， 1997，56(1):81-86.

[4]BRUTMAN L.On rational interpolation to |x| at adjusted Chebyshev nodes[J].Journal of Approximation Theory，1998，95(1):146-152.

[5]ZHAO Yi， ZHOU S P.Some remarks on rational interpolation to |x| [J].Journal of Mathematical Research &Exposition，2003，23(1):65-70.

[6]REVERS M.The divergence of Lagrange interpolation for |x|αat equidistant notes[J].Journal of Approximation Theory，2000，103(2):269-280.

[7]张慧明，段生贵，李建俊.|x|α在第二类Chebyshev结点的有理插值[J].四川师范大学学报(自然科学报)，2015，38(06):889-892.

Rational Interpolation to |x|αon a Set of Interpolation Nodes

JIANG Yinting, ZHAO Yi, XU Jianghai

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

rational interpolation; Newman-αtype rational operator; density; approximation order

10.13954/j.cnki.hdu.2017.01.020

2016-05-25

国家自然科学基金资助项目(11601110)

蒋银停(1992-),男,安徽宿州人,硕士研究生,函数逼近论.通信作者：赵易副教授；E-mail：zhaoyi@hdu.edu.cn.

O174.41

A

1001-9146(2017)01-0091-04