脉冲序列控制BIFRED变换器的脉冲组合和电压纹波
2017-03-02李芳苑吴志敏张海明
李芳苑, 吴志敏, 张海明
(1.南京信息职业技术学院电子信息学院,江苏 南京 210017;2.常州大学信息科学与工程学院,江苏 常州 213164)
脉冲序列控制BIFRED变换器的脉冲组合和电压纹波
李芳苑1, 吴志敏2, 张海明2
(1.南京信息职业技术学院电子信息学院,江苏 南京 210017;2.常州大学信息科学与工程学院,江苏 常州 213164)
升压式-反激式集成的整流/储能直流-直流(BIFRED)变换器是由Boost电路与反激式电路集成实现的,具有电路简单、成本低、负载范围宽等优点,工程应用价值较高。脉冲序列(PT)控制技术是一种新的离散控制技术,比较适用于BIFRED变换器的输出电压调节控制,但PT控制存在着输出电压纹波较大的缺点,因此研究PT控制BIFRED变换器的输出电压纹波具有重要的物理意义。为了更好地表征工作在双断续导电模式(DCM-DCM)下的PT控制BIFRED变换器的电压调节控制性能,通过求解在1个开关周期内流过副边二极管的平均电流,得到了在1个开关周期内高、低功率脉冲作用下的输出电压变化量,由此获得了不同负载时PT控制DCM-DCM BIFRED变换器的控制脉冲组合,并进一步确定了相应的输出电压纹波。通过PSIM仿真软件和硬件试验,得到了不同负载下的时域波形,验证了控制脉冲组合、输出电压纹波理论分析的正确性及控制方案的可行性。
双断续导电模式; 脉冲序列控制; BIFRED变换器; PSIM; 电压; 功率; 电路; 动态响应
0 引言
随着对开关电源瞬态特性和鲁棒性的要求越来越高,传统脉冲宽度调制所体现的局限性也越发引起人们的重视[1-2]。为了提高开关电源的电压调节性能,提出了一种新型脉冲序列(pulse train,PT)控制技术[3-4]。与传统的脉冲宽度调制(pulse width modulation,PWM)控制技术不同,PT控制通过改变预先设定的两个相同频率、不同占空比的脉冲组合形式,来实现对输出电压的调节。PT控制具有动态响应速度快、控制电路实现简单等优点[5-7],但也存在输出电压纹波较大的缺点,所以研究PT控制开关功率变换器的输出电压纹波特性具有重要意义[8-10]。
四阶隔离式升压式-反激式集成的整流/储能直流-直流(boost integrated flyback rectifier/energy storage DC-DC,BIFRED)变换器是由Boost变换器和反激式变换器集成实现的[11-13],两者均工作于电流断续导电模式(discontinuous conduction mode,DCM),也称为双断续导电模式(dual discontinuous conduction mode,DCM-DCM)[14]。由于BIFRED变换器存在多种工作模式,动力学建模及其理论分析相当复杂,使得对BIFRED变换器的研究受到了极大限制[11,14],因此关于其输出电压纹波特性的研究成果并不多。本文分析了随负载变化时PT控制DCM-DCM BIFRED变换器的工作原理,并根据每个控制脉冲周期内其变换器输出电压的变化量,推算出与负载相关联的控制脉冲组合与输出电压纹波量,进而进行数值仿真和硬件试验,验证了结果的正确性。
1 PT控制BIFRED变换器的工作原理
主电路由负载电阻R、功率MOS开关管S、二极管D1与D2、储能与输出电容C1与C2、输入与励磁电感L1与L2、隔离变压器等电路元件组成。隔离变压器的原、副边绕组匝比为N∶1。假设流过L1与L2的电流分别为i1与i2,C1与C2两端电压分别为U1与U2,负载输出电压为Uo,且有Uo=U2。PT控制BIFRED变换器的电路原理图如图1所示。

图1 电路原理图
在每个控制脉冲周期的开始时刻,PT控制器检测并采样BIFRED变换器的输出电压Uo,且与基准电压Uref进行比较。当输出电压Uo低于基准电压Uref时,PT控制器选择高功率脉冲PH作为控制信号;当Uo高于Uref时,PT控制器选择低功率脉冲PL作为控制信号。高、低功率脉冲PH和PL具有相同的频率和不同的占空比,PT控制器通过选择PH和PL来控制主电路中开关管S的导通时间,从而对Uo进行调节。
2 控制脉冲组合和输出电压纹波
2.1 高低功率控制脉冲组合
PT控制BIFRED变换器在DCM-DCM模式下工作时,对于在每个控制脉冲周期的起始或结束时刻,通过副边二极管D2的电流为零,故可以求出在一个控制脉冲周期内流过副边二极管D2的平均电流,并进一步求得在高功率脉冲PH或低功率脉冲PL作用下输出电压Uo的变化量。
稳态时,BIFRED变换器在DCM-DCM模式下的不同工作模式所对应的输入电感电流i1、励磁电感电流i2和副边二极管电流iD2的时域波形如图2所示[14]。图2中:T为开关周期;t0、t5分别为第n个开关周期的开始、结果时刻;t1、t2和t4分别为S、D1和D2由导通至关断的切换时刻;t3为i2下降到i0平均值的时刻;τ1、τ2、τ3和τ4分别为t0~t1、t1~t2、t3~t4、t4~t5的时间间隔;i1(t1)、i2(t1)和iD2(t1)分别为在t1时刻的电流值,也是一个控制脉冲周期内i1、i2和iD2的最大值;i0为负载电流。
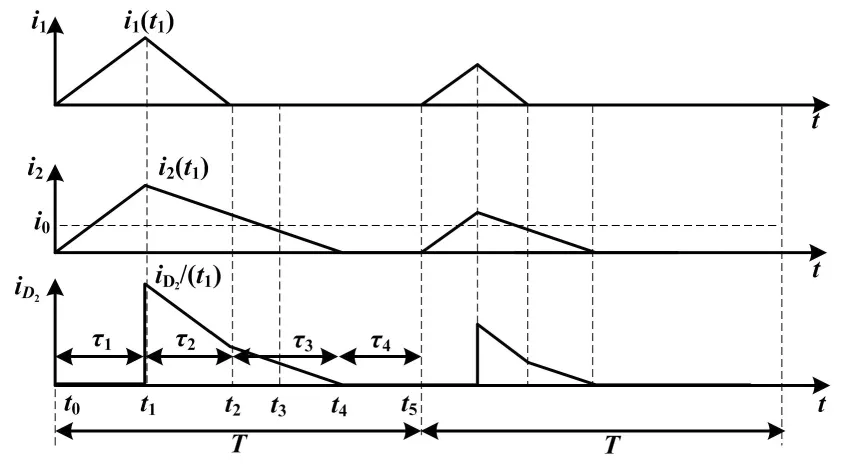
图2 BIFRED变换器i1、i2和iD2的时域波形
通过副边二极管D2的平均电流ID2可以表示为:
ID2=[(τ2+τ3)/i2(t1)+Nτ2i1(t1)]/2T
(1)
在每个控制脉冲周期开始时刻,输入电感电流i1始终为零。在τ1期间,i1线性增加,恒定斜率为E/L1。当变换器工作在τ2期间,i1开始下降,即L1对变压器的初级侧以及C2放电。此时,i1(t1)既是τ1阶段的结束值,也是τ2阶段的初始值,可分别表示为:
i1(t1)=τ1E/L1
(2)
i1(t1)=τ2(U1+NU1-E)/L1
(3)
同理,i2(t1)也可分别表示为:
i2(t1)=τ1U1/NL2
(4)
i2(t1)=(τ2+τ3)U2/L2
(5)
储能电容C1的电流iC1、电压U1的稳态时域波形如图3所示。图3中的iC1与时间轴t构成的阴影部分的面积,表示在一个开关周期内储能电容C1的电荷变化量。

图3 储能电容C1的电流iC1和电压U1时域波形
由电荷守恒原理得:
τ1i2(t1)/N=τ2i1(t1)
(6)
将式(2)~式(4)代入式(6),并整理得:
(7)
假设U2=Uref,可将式(7)改写为:
(8)

因此,有:
(9)
由式(4)和式(6),可分别求出U1和τ2为:
U1=NL2i2(t1)/τ1
τ2=τ1i2(t1)/Ni1(t1)
(10)
由式(5)可得τ3为:
τ3=i2(t1)L2/Uref-τ2
(11)

(12)
从式(12)可以看出,平均电流ID2的值只与i2(t1)有关,而i2(t1)值已求出,则可得流过副边二极管D2的平均电流ID2。
当以一个高功率脉冲PH作为控制信号时,在一个控制脉冲周期内输出电压的变化量ΔUH可近似为:
(13)
同理,当以一个低功率脉冲PL作为控制信号时,在一个控制脉冲周期内输出电压的变化量ΔUL可近似为:
(14)
由式(13)和式(14)可知,ΔUH和ΔUL都是关于负载电阻R的函数。
当PT控制DCM-DCM BIFRED变换器工作在稳定状态时,在控制脉冲循环周期内,输出电容的电荷变化量为零,则有:
μHΔUH+μLΔUL=0
(15)
即:
(16)
式中:μH和μL分别为高低脉冲的个数。
PT控制BIFRED变换器的电路参数如表1所示。表1中,R的范围为4~20 Ω。

表1 PT控制BIFRED变换器的电路参数
由式(13)、式(14)和式(16)可分别绘制出ΔUH、-ΔUL和μH/μL、μL/μH与负载电阻R的关系曲线,如图4所示。
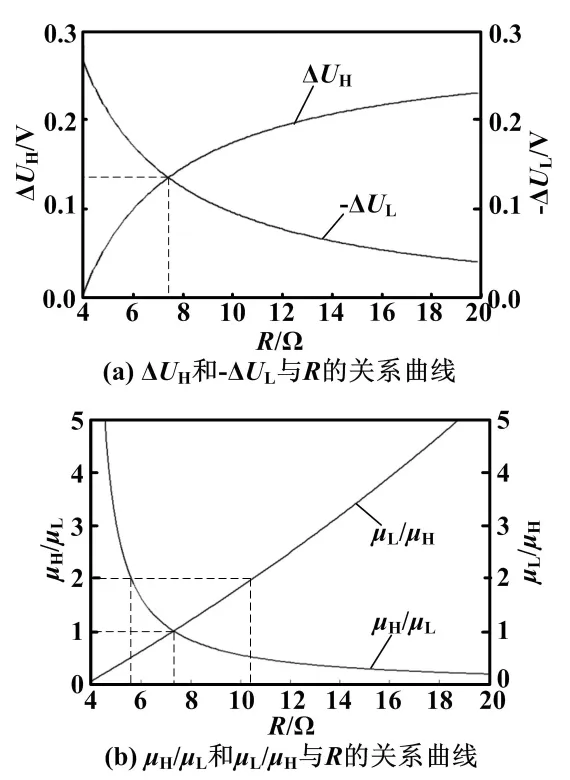
图4 ΔUH和-ΔUL、μH/μL和μL/μH与负载R的关系曲线
从图4(a)可以看出,当PT控制DCM-DCM BIFRED变换器在一个控制脉冲循环周期内工作,PH和PL所形成的输出电压变化量是相等的。同时可知,随着R的增大,即负载功率降低,ΔUH增加,-ΔUL减小。反之,随着R减小,即负载功率增加,ΔUH减小,-ΔUL增大。ΔUH与-ΔUL在R=7.3 Ω处有一个交点,高功率脉冲与低功率脉冲的数相等,且控制脉冲组合为1PH-1PL,其循环周期数为2。从图4(b)可以看出,随着负载不断增大,μH/μL的比值不断减小,即PH的个数逐渐小于PL的个数;反之,随着负载不断减小,PH的数量逐渐大于PL的数量。当R≈7.3 Ω时,PH数量与PL数量相等,控制脉冲组合为1PH-1PL,其循环周期数为2。当控制脉冲循环周期数为3时,其控制脉冲组合有两种,分别为2PH-1PL和1PH-2PL,即μH/μL= 2和μL/μH= 2;而对应的负载R分别约为5.6 Ω和10.6 Ω。
2.2 输出电压纹波分析
输出电压纹波是PT控制DC-DC开关功率变换器的重要性能指标。当控制脉冲组合不同时,输出电压纹波也不同。
当PT控制DCM-DCM BIFRED变换器工作在稳定状态时,高、低功率脉冲的输出电压变化量在每个控制脉冲周期内是不变的。通过计算高、低功率脉冲对应的输出电压变化量,作为PT控制开关变换器在一个控制脉冲周期内的输出电压纹波[8]。
若PT控制DCM-DCM BIFRED变换器的控制脉冲循环周期数为2PH-1PL,输出电压纹波如图5所示。

图5 脉冲循环周期为2PH-1PL时的输出电压纹波
其输出电压纹波为:
ΔU≈ΔUH+ΔUH,tOFF
(17)
同理,当PT控制DCM-DCM BIFRED变换器的控制脉冲循环周期由μH个PH和μL个PL组成时,其输出电压纹波为:
ΔU≈(μH-1)ΔUH+ΔUH,tOFF
(18)
式中:ΔUH,tOFF为S关断时,即BIFRED变换器工作在τ2和τ3阶段的输出电压变化量。
(19)
3 电路仿真和硬件试验
利用PSIM仿真软件,根据表1所示的电路参数,对PT控制BIFRED变换器进行电路仿真。在负载R不同的情况下,PT控制BIFRED变换器的输入电感电流i1和输出电压Uo的时域波形如图6和图7所示。
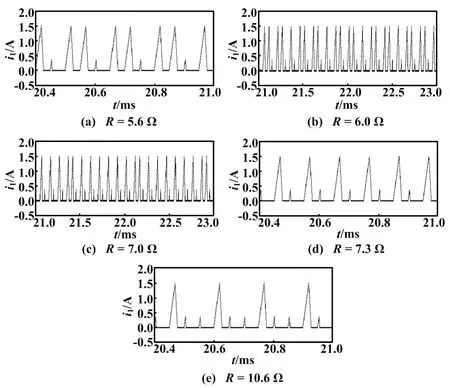
图6 不同负载时i1的仿真波形

图7 不同负载时Uo的仿真波形
输入电感电流i1的仿真波形表明该变换器均工作在DCM模式,且运行在多周期状态。当R分别为5.6 Ω和10.6 Ω时,BIFRED变换器均为周期3振荡,相应的控制脉冲序列分别为2PH-1PL和1PH-2PL,分别如图6(a)、图7(a)和图6(e)、图7(e)所示。当R=6.0 Ω时,BIFRED变换器为周期8振荡,控制脉冲序列为2(2PH-1PL)-1(1PH-1PL),如图6(b)、图7(b)所示。当R=7 Ω时,BIFRED变换器为周期15振荡,控制脉冲序列为(2PH-1PL)-6(1PH-1PL),如图6(c)、图7(c)所示。当R=7.3 Ω时,BIFRED变换器为周期2振荡,控制脉冲序列为1PH-1PL,如图6(d)、图7(d)所示。
在一个控制脉冲循环周期内,对于不同负载R,PT控制DCM-DCM BIFRED变换器的高、低功率控制脉冲组合的电路仿真结果及理论计算结果如表2所示。图6、图7和表2表明了该变换器控制脉冲组合的PSIM电路仿真结果与理论分析一致。

表2 不同负载下控制脉冲组合计算结果
以R=5.6 Ω为例,说明在该负载下PT控制DCM-DCM BIFRED变换器在一个控制脉冲循环周期内输出电压纹波的变化量。进行PSIM电路仿真时,输入电感电流i1和输出电压Uo的时域波形放大图如图8所示。由图8可知,控制脉冲组合为2PH-1PL,输出电压纹波变化量的仿真值为0.34 V。由式(18)可计算出输出电压纹波变化量的理论值为0.36 V。由此表明,仿真值与理论值基本一致。

图8 当R=5.6 Ω时i1和Uo的仿真波形
通过设计硬件电路,可进一步验证理论分析的正确性。在硬件电路中,选取的主要元器件型号有[14]:开关管IRF640N、二极管MBR2035、比较器LM319、D触发器74LS74、与门74LS08、或门74LS32、驱动电路IR2125等。高、低功率脉冲采用FPGA技术生成,输出电容采用22个10 μF的贴片电容并联实现。从示波器上捕获的试验波形可观察到,PT控制BIFRED变换器的输入电感电流i1和励磁电感电流i2均工作在DCM模式,当负载R的电阻值分别选取为5.6 Ω、6.0 Ω、7.0 Ω、7.3 Ω和10.6 Ω时,相对应的控制脉冲组合分别为2PH-1PL、5PH-3PL、8PH-7PL、1PH-1PL和1PH-2PL。此外,当R=5.6 Ω时,PT控制BIFRED变换器在一个控制脉冲循环周期内输出电压纹波变化量的测量值约为0.35 V。由此表明,硬件试验结果与电路仿真结果基本一致。
4 结束语
脉冲序列控制技术通过改变预先设定好的控制脉冲组合形式来实现对开关变换器输出电压的调节,其控制电路简单,具有快速的动态响应性能。通过分析每个开关周期内高、低功率脉冲控制下输出电压纹波的变化量,得到了不同负载条件下PT控制DCM-DCM BIFRED变换器的高、低功率控制脉冲在一个控制脉冲循环周期内的组合形式,以及对应的输出电压纹波解析式,为实际工程电路设计的参数选择提供了十分有价值的理论参考。最后,通过PSIM电路仿真和硬件电路试验,验证了上述理论分析的正确性。
[1] 史国栋,董伟,包伯成,等.开关DC-DC变换器恒频定关断时间控制技术研究[J].自动化仪表,2016,37(1):88-92.
[2] 史国栋,杨艳,张希,等.电感与负载对V2 控制Buck变换器的动力学影响[J].自动化仪表,2016,37(4):12-20.
[3] FERDOWSI M,EMADI A,TELEFUS M,et al.Pulse regulation control technique for flyback converter[J].IEEE Transactions on Power Electronics,2005,20(4):798-805.
[4] TELEFUS M,SHTEYNBERG A,FERDOWSI M,et al.Pulse train control technique for flyback converter[J].IEEE Transactions on Power Electronics,2004,19(3):757-764.
[5] QIN M,XU J P.Multiduty ratio modulation technique for switching DC-DC converters operating in discontinuous conduction mode[J].IEEE Transactions on industrial Electronics,2010,57(10):3497-3507.
[6] 沙金,包伯成,许建平,等.脉冲序列控制电流断续模式Buck变换器的动力学建模与边界碰撞分岔[J].物理学报,2012,61(12):120501.
[7] SHA J,XU J P,BAO B C,et al.Effects of circuit parameters on dynamics of current-mode pulse train controlled buck converter[J].IEEE Transactions on Industrial Electronics,2014,61(3):1562-1573.
[8] 牟清波,许建平,秦明,等.脉冲序列控制反激变换器输出电压纹波和脉冲组合方式[J].电工技术学报,2010,25(9):101-107.
[9] 许建平,牟清波,王金平,等.脉冲序列控制DCM Buck变换器输出电压纹波研究[J].电机与控制学报,2010,14(5):1- 6.
[10]吴志敏,包伯成,张希.脉冲序列控制DCM Boost变换器的控制脉冲组合和输出电压纹波研究[J].电测与仪表,2013,50(3):75-80.
[11]FERDOWSI M,EMADI A,TELEFUS M,et al.Suitability of pulse train control technique for BIFRED converter[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(1):181-189.
[12]WILLERS M J,EGAN M G,DALY S,et al.Analysis and design of a practical discontinuous-conduction-mode BIFRED converter[J].IEEE Transactions on Industrial Electronics,1999,46 (4):724-733.
[13]FERDOWSI M,EMADI A.Pulse regulation control technique for integrated high-quality rectifier-regulators[J].IEEE Transactions on Industrial Electronics,2005,52(1):116-124.
[14]史国栋,张海明,包伯成,等.脉冲序列控制双断续导电模式BIFRED变换器的动力学建模与多周期行为[J].物理学报,2015,64(1):010501.
Pulse Combination and Voltage Ripple in Pulse Train Controlled BIFRED Converter
LI Fangyuan1, WU Zhimin2, ZHANG Haiming2
(1.School of Electronic Information,Nanjing College of Information Technology,Nanjing 210017,China; 2.School of Information Science and Engineering, Changzhou University,Changzhou 213164,China)
The boost integrated flyback rectifier/energy storage DC-DC (BIFRED) converter is integrated by a boost circuit and a flyback circuit;its advantages are simple circuitry,low cost,wide load range,and higher engineering applicable value.Pulse train (PT) control technology is a new type of discrete control technology,which is more suitable for output voltage regulation control of BIFRED converter.However,there is disadvantage of larger output voltage ripple in PT control;therefore,the investigation of output voltage ripple in PT controlled BIFRED converter has important physical significance.To better characterize voltage regulation control performance of PT controlled BIFRED converter operating in dual discontinuous conduction mode (DCM-DCM),the output voltage variations respectively driven by high and low power pulses in a switching cycle are derived by solving the average current flowing through the secondary diode in a switching cycle,from which the control pulse combinations of PT controlled DCM-DCM BIFRED converter under different loads are obtained and the corresponding output voltage ripples are further determined.Based on PSIM circuit simulations and hardware experiments,the time domain waveforms under different load resistances are obtained.The correctness of the theoretical analysis of control pulse combinations and output voltage ripples and the feasibility of control scheme are verified.
Dual discontinuous conduction mode (DCM-DCM); Pulse train (PT) control; BIFRED converter; PSIM; Voltage; Power; Circuit; Dynamic response
国家自然科学基金青年资助项目(51407054)、常州市基础研究计划(自然科学基金)资助项目(CJ20159026)
李芳苑(1988—),女,硕士,讲师,主要从事智能产品开发、电子信息工程及集成电路设计等方向的研究。E-mail:lify@njcit.cn。 吴志敏(通信作者),女,硕士,讲师,主要从事电能变换与控制技术的研究。E-mail:wuzhimin@cczu.edu.cn。
TH86;TP13
A
10.16086/j.cnki.issn 1000-0380.201702002
修改稿收到日期:2016-03-05
