盾构隧道局部不同部位漏水对隧道和地表沉降的影响
2017-03-02姚杰戴轩郑刚孙佳羽
姚杰,戴轩,郑刚,孙佳羽
(1.天津大学滨海土木工程结构与安全教育部重点实验室,天津 300072;2.天津大学水利工程仿真与安全国家重点实验室,天津 300072;3.天津市市政工程设计研究院,天津 300051)
盾构隧道局部不同部位漏水对隧道和地表沉降的影响
姚杰1,2,戴轩3,郑刚1,2,孙佳羽1,2
(1.天津大学滨海土木工程结构与安全教育部重点实验室,天津 300072;2.天津大学水利工程仿真与安全国家重点实验室,天津 300072;3.天津市市政工程设计研究院,天津 300051)
针对富水地区中隧道管片局部在隧道不同区域发生漏水灾害情况,建立三维流固耦合模型,对比分析了不同位置发生漏水以及在不同漏水量下地表沉降、隧道变形规律。研究表明隧道漏水位置越靠近隧道底部时,地表沉降最大值越小,沉降槽呈现宽而浅,漏水量越大,沉降越明显;隧道局部漏水会使隧道纵向沉降不均匀,使得隧道环缝张开,漏水位置越靠近隧道底部,环缝张开量越大,张开量与流量之间成正比,从而验证了隧道漏水与隧道变形耦合发展的机理。
隧道工程;漏水位置;灾害;沉降;隧道变形
0 引言
在饱和软土地区,盾构隧道不均匀沉降引起隧道发生纵向弯曲,导致隧道环缝张开,引发的隧道渗水的情况十分常见。隧道渗水引起隧道进一步变形,影响隧道运营安全,甚至引发更为严重的漏水漏砂事故,国内的金山引水隧道和前苏联的圣彼得堡1号线隧道都曾因隧道漏水漏砂而被迫终止运营[1-2]。
大多数学者[3-5]采用二维模型进行数值模拟计算,但隧道发生局部渗水主要集中在环缝、纵缝、螺栓孔等位置,隧道漏水问题实质是一个复杂的三维问题,二维模型难以反映隧道的纵向变形情况,在隧道纵向受力上,忽略了隧道自身对该环隧道管片的约束作用;在水的补给上,二维模型中水的补给全部来自于漏点横向两侧,忽略了来自隧道纵向上的补给。
针对二维模型的不足,有的学者[6]采用三维模型进行了渗水模拟,从二维到三维,学者们针对隧道的长期渗水行为研究成果斐然,但对于隧道局部渗水流量的增大导致隧道纵向变形,从而引起灾害的情况关注较少。此外,隧道发生漏水灾害后在短期即可对隧道和土体造成较大影响,目前缺乏相关研究。
笔者建立了三维模型对隧道局部漏水问题进行流固耦合分析,分析了隧道不同漏水位置、流量大小对地表沉降及隧道变形的影响。本文仅研究盾构隧道局部漏水(土颗粒没有漏出)这种情况下的影响,更为极端的土体流失的情况将另撰文研究。
1 盾构隧道局部渗漏的数值模拟
1.1 三维数值计算模型
天津市地铁2号线建国道—天津站区间隧道采用土压平衡盾构施工,隧道顶部的平均埋深为10 m,盾构管片厚度350 mm,管片宽度1.2 m,管片外径 6.2 m,混凝土管片的弹性模量为34.5 GPa,泊松比为0.16,本文以该工程为背景建立数值模型。采用FLAC3D有限差分软件,建立可考虑流固耦合的三维模型,如图1所示。模型计算域横向(X轴向)长度为120 m,纵向(Y轴向)长度为120 m,深度(Z轴向)为53 m,模型坐标原点取在模型地表中心处,隧道中心轴线沿Y向,位于X=0 m,Z=-13 m地表之下13 m处,经过多次试算,该计算域尺寸基本满足边界效应的影响要求。同时,模型网格在隧道附近进行了加密。

图1 有限差分计算模型Fig.1 Modeloffinite difference method model
本文选择M-C模型进行隧道漏水分析和计算,J.H.Shin等[3-5]文章的分析结果也验证了M-C模型对于隧道渗水引发土体变形计算问题的适应性,故本文采用M-C模型进行隧道的漏水分析和计算。
按照所选定的本构模型,数值计算所需要的土层物理力学参数如表1所示。

表1 土层参数表Table 1 Parameters of soillayers
1.2 隧道刚度选取
盾构隧道管片接头较难模拟,很多学者采用刚度等效折减的方法模拟接头的作用[7-8]。本文同样引入横向刚度有效率和纵向刚度有效率来考虑隧道接头对其刚度的影响,即隧道刚度各向异性[7]。
根据各向同性材料的弹性矩阵对称性可知:

在隧道横截面上,弹性模量通过横截面上的横向刚度有效率ηxy进行折减,而在隧道纵向上,弹性模量通过纵向刚度有效率ηz进行折减,即:

横断面上的剪切模量与横断面弹性模量有关,剪切模量Gxy与Ex和Ey同比例折减;而纵向上的剪切模量与弹性模量相互独立,根据何川等[8]的研究,可采用纵向上的抗剪切刚度折减系数进行折减:
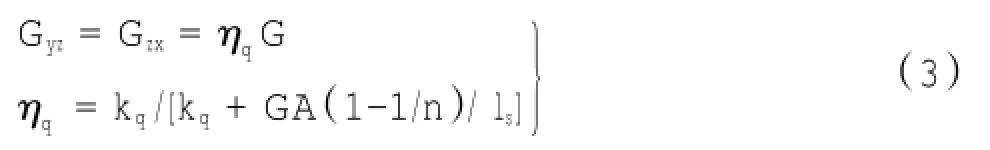
式中:下标x,y和z为各向同性材料的3个主方向;E为原混凝土的弹性模量;G为原混凝土的剪切模量;kq为纵向接头螺栓的剪切刚度;A为管片环横截面面积;ls为单环管片衬砌的幅宽。
根据钟小春等人[9]的研究,横向刚度有效率的取值在0.4~0.8左右,黄宏伟等[10]也通过模型试验证实隧道横向刚度有效率在0.7左右,本文中模型横向刚度有效率取值为0.7。
隧道衬砌层纵向变形主要由结构弯曲变形引起,钟小春等[11]研究表明纵向刚度有效率取值和隧道横向刚度有效率、环缝处的螺栓数量、管片环宽度,纵向螺栓预紧力等因素有关。本文横向刚度有效率取值为0.7,天津地铁二号线隧道结构参数如表2所示,根据钟小春的研究成果,得到纵向刚度有效率在0.1左右,故本文中模型纵向刚度有效率取值为0.1。模型中隧道参数见表3。

表2 盾构隧道的主要结构参数Table 2 Structuralparameters of shield segment

表3 衬砌管片参数Table 3 Parameters of tunnelsegment
1.3 隧道漏水的模拟及工况
潘海泽等[12]根据衬砌渗漏水量的大小及渗漏状态将隧道渗漏水灾害分为渗润、滴水、流水、喷水、淋瀑5个等级,在其调查的95座隧道之中有7%的隧道存在缝漏喷水现象,根据经验,一处喷水的漏水量可达1 m3/d,隧道在某一局部区域产生5处喷水即可致灾,即产生5 m3/d漏水量,以此漏水量为基准建立隧道局部漏水的灾害环境。
本文采用Shin等[3]提出的等效衬砌渗透系数的方法来实现漏水,通过改变衬砌的渗透系数来模拟漏水。衬砌渗透系数是其劣化、裂缝等的综合反映。通过试算的方法,不断调整衬砌与土体渗透系数比,最终确定不同工况下漏水位置处衬砌的渗透系数取值。
隧道发生漏水的位置主要集中在隧道环缝、纵缝以及螺栓接头等地方[4],为了反映隧道局部不同位置的漏水情况,将隧道漏水位置选在隧道模型中部一环管片(Y=-0.6 m到Y=0.6 m)的4个区域,如图1和图2所示。
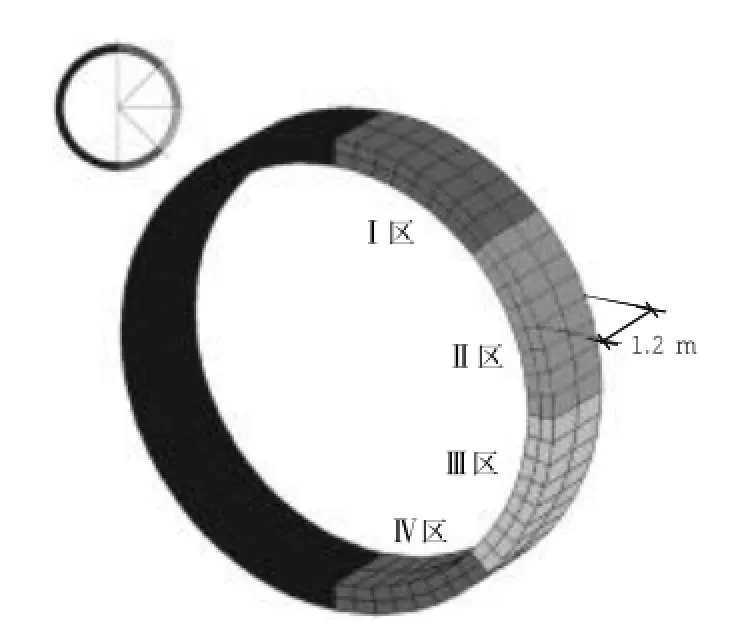
图2 渗漏隧道分区Fig.2 Different zones of leakage tunnel
针对在这4个区域发生相同的漏水量以及在同一区域发生不同的漏水量建立了7种工况,如表4所示。
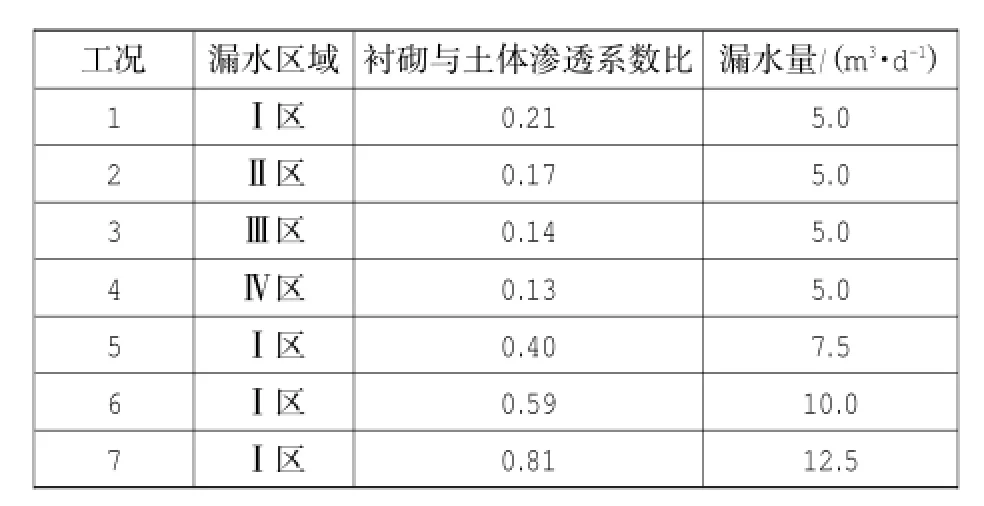
表4 计算工况Table 4 Calculated working conditions
1.4 计算分析步骤及边界条件设置
本文主要研究隧道建成之后运营期间发生漏水所产生的影响,在前期首先模拟盾构隧道的开挖,主要的分析步骤如下:1)初始地应力平衡;2)模拟隧道开挖;3)设置漏水区域,通过调整衬砌渗透系数确定漏水量,进行漏水模拟。
模型位移边界条件为:地表为自由边界;模型土体的侧向边界和底面边界约束各自法向位移,模型隧道始发和接收端也约束其转动位移。模型中地下水位位于地表以下1.5 m,并在模型侧面施加了孔压边界条件,模型侧面水位以下施加梯度为9.8 kPa/m的静水压力以模拟水源补给;模型底面和隧道不透水部分设置为不透水边界;隧道发生漏水区域在漏水期间设置为透水边界,并将该部分隧道内侧孔压设置为0。
2 隧道局部漏水的影响分析
2.1 隧道局部漏水对地表沉降的影响
图3是隧道局部不同位置发生漏水时地表最大沉降随时间的变化情况,图4为200 d时隧道局部不同位置漏水时横断面处地表沉降曲线。
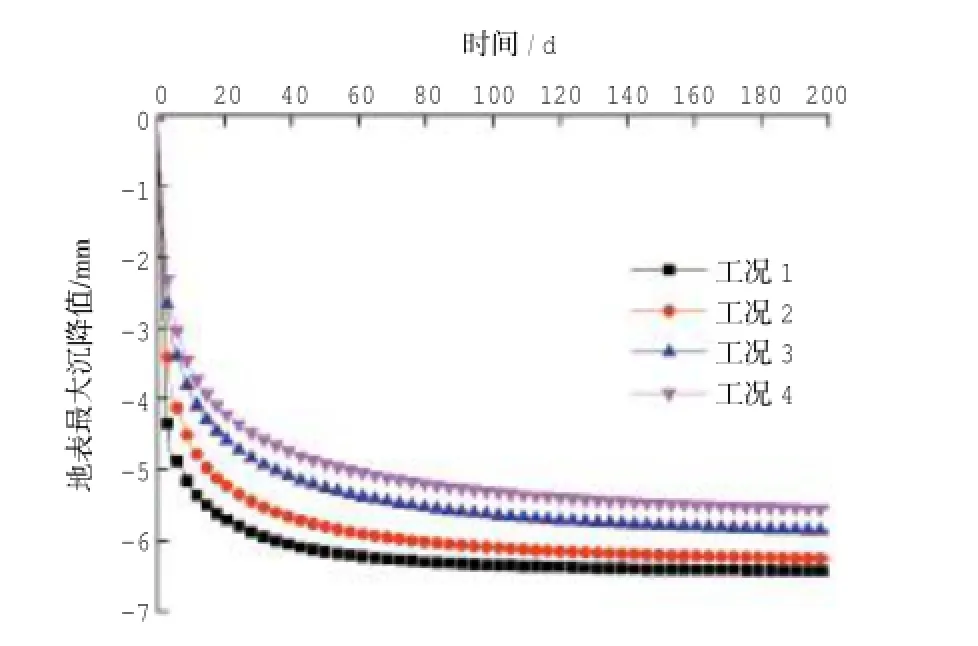
图3 不同漏水位置地表沉降最大值随时间变化曲线Fig.3 Variations of maximum surface settlement with time atdifferentleakage positions

图4 不同漏水位置地表沉降槽Fig.4 Surface settlementtroughs atdifferentleakage positions
综合这两张图,可以得出以下规律:
1)隧道局部发生漏水之后,前72 h地表迅速发生沉降,之后地表沉降缓慢发展,漏水灾害的治理应该在72 h内展开[5]。
2)漏水量相同时,漏水位置越靠近隧道顶部,地表最大沉降量越大,隧道局部Ⅰ区漏水相比于Ⅳ区漏水时地表最大沉降提高16%,分析其原因,在三维模型之中考虑了隧道纵向的约束作用,隧道不能轻易随着土动,当漏水位置降低,使得更多的土体固结发生在隧道下侧,这部分土体的变形需绕过隧道传递到地表,隧道阻碍土体变形的向上传递。而二维模型无法考虑隧道的纵向约束,往往隧道随着土体运动,从而得出相反结论(漏点越低,沉降值越大[10-11]),与隧道实际工作状态不符。这种隧道对土体变形的扩散效应最终使得隧道局部漏水位置越低,地表沉降最大值反而越小。
3)地表沉降槽形状接近peck曲线,隧道位置靠近隧道底部时,地表沉降槽呈现宽而浅,而当漏水位置靠近隧道顶部时,地表沉降槽呈现窄而深,如果上方存在建筑物或者刚性路面,更可能因为不均匀沉降而发生开裂。
4)由于漏水位置的偏离,会使得沉降槽最低点偏离隧道中心竖轴,由于隧道的纵向刚度的影响,隧道下方的土体固结变形需绕过隧道传递到地表,所以工况4和工况3相比于工况1和工况2沉降槽最低点偏离隧道中心竖轴更远,这也进一步佐证了第2)条中土体变形扩散的推论。
图5是不同漏水量引起的地表最大沉降随时间的变化情况。
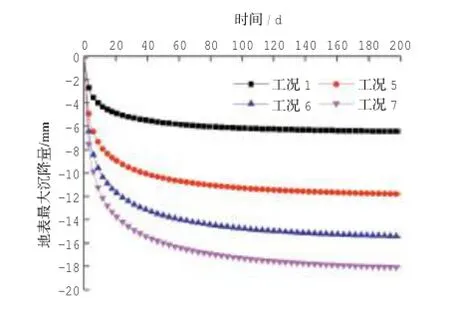
图5 不同漏水流量下地表沉降最大值随时间变化曲线Fig.5 Variations of maximum surface settlement with time at different leakage flow rates
图6、图7为隧道局部在不同漏水量下第200天时横断面处地表沉降曲线和最大沉降值。

图6 不同漏水量地表沉降槽Fig.6 Surface settlement troughs atdifferent leakage flow rates

图7 不同漏水量下地表最大沉降值Fig.7 Maximum surface settlement at different leakage flow rates
综合图5~图7,可以得出以下规律:
1)漏水量增大,会使得地表沉降发展更迅速,同时沉降达到稳定所需的时间越长。
2)漏水量增大,地表沉降越大,漏水影响的范围也越广,工况6相比于工况1漏水量提高1倍,地表沉降最大值提高2.4,接近等比例,吴怀娜等[13]也得到类似的规律。相比隧道局部不同漏水位置对地表沉降的影响,漏水量差异造成的影响更加明显。
2.2 隧道局部漏水对隧道的影响
图8和图9分别为隧道局部不同位置漏水和不同漏水量下隧道最大沉降值随时间变化曲线,结合图3和图5,可以看出隧道沉降的发展相比于地表沉降更平缓一些,漏水位置越靠下,隧道下部固结的土体越多,使得隧道沉降越大,工况4相比于工况1,隧道沉降最大值增大112%;当流量增大时,隧道下部土体固结值增大,使得隧道最大沉降量也增大。

图8 不同漏水位置隧道沉降最大值随时间变化曲线Fig.8 Variations of maximum tunnelsettlement with time at different leakage positions

图9 不同漏水流量下漏水隧道沉降值随时间变化曲线Fig.9 Variations of maximum tunnelsettlementwith time at different leakage flow rates
不同工况下隧道与地表之间沉降最大值之间的比值(沉降比)如表5所示,各工况的沉降比位于0.33~80之间,漏水位置越低,沉降比越大,这与刘印[4]二维渗漏水模型的计算结果一致。随着漏水量增大,沉降比增加并不明显。

表5 隧道与地表之间沉降最大值的比值Table 5 Ratio of maximum tunnelsettlement and maximum surface settlement
隧道发生漏水后,引起隧道周围土体的固结,最终引发隧道的下沉,图10和图11分别为隧道局部不同位置漏水和不同漏水量下隧道中心轴线的沉降曲线,隧道局部漏水会使得隧道纵向沉降不均匀,漏水位置越靠下,隧道沉降的范围越广;漏水量增大,隧道沉降的范围越广。
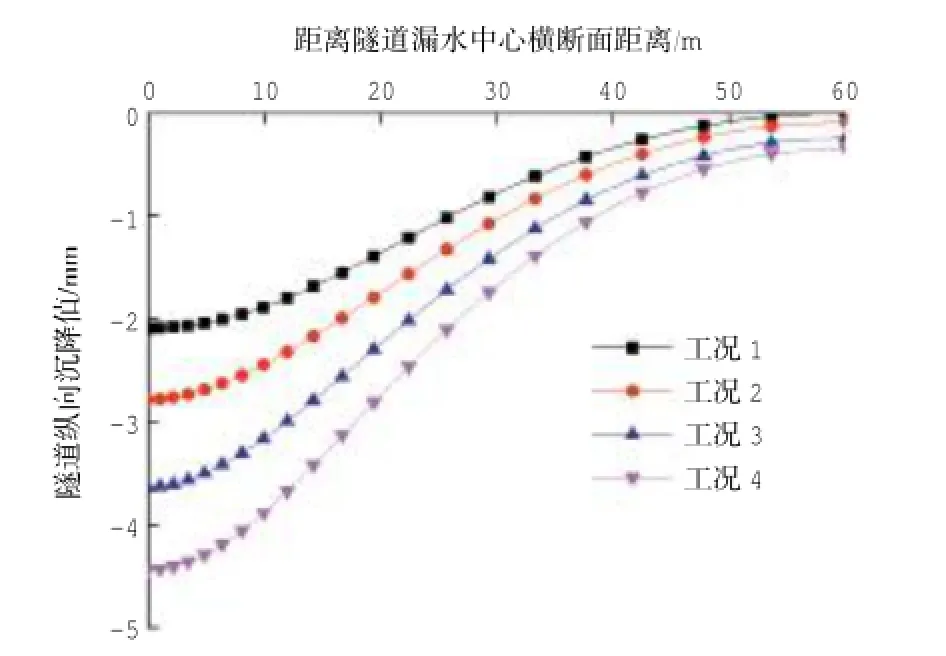
图10 不同位置漏水隧道纵向沉降曲线Fig.10 Tunnellongitudinalsettlementcurve atdifferent leakage positions
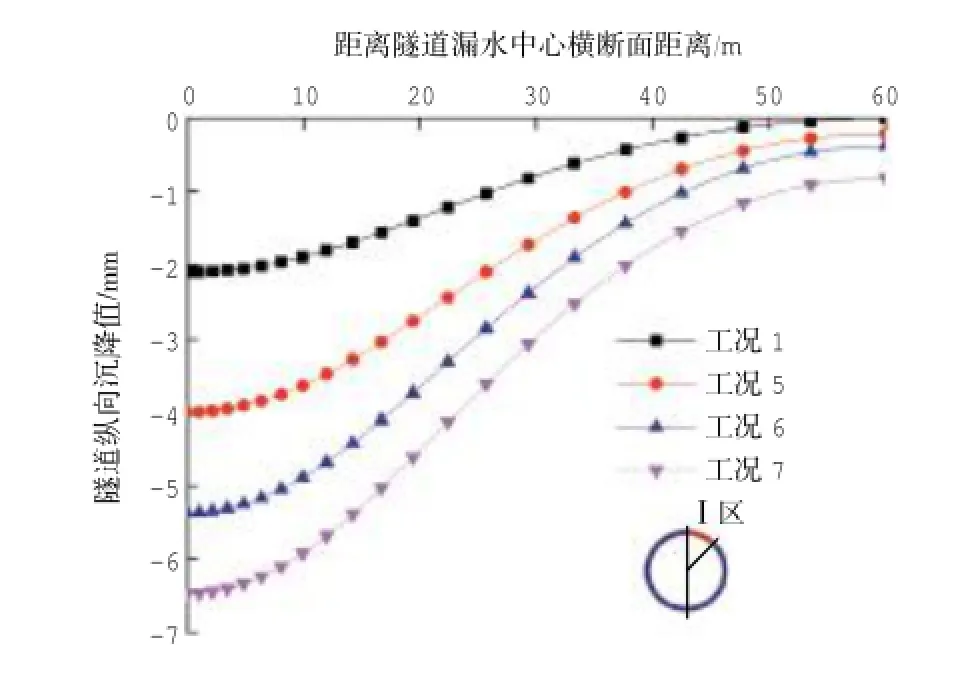
图11 不同流量下隧道纵向沉降曲线Fig.11 Tunnellongitudinalsettlement curve at different leakage flow rates
隧道的不均匀沉降不仅影响列车的运营,这种隧道曲率上的变化更会使得环缝进一步张开[13],刘印等[14]也通过隧道漏水机理分析验证了隧道曲率对于隧道环缝张开量的显著影响。隧道漏水引起的隧道纵向曲率半径的变化见表6,在笔者计算的几种工况下,最小曲率半径为44.5 km,继续发展可能超过《地铁隧道保护条例》规定由外界因素引起的隧道曲率半径不小于15 km的限制限值。
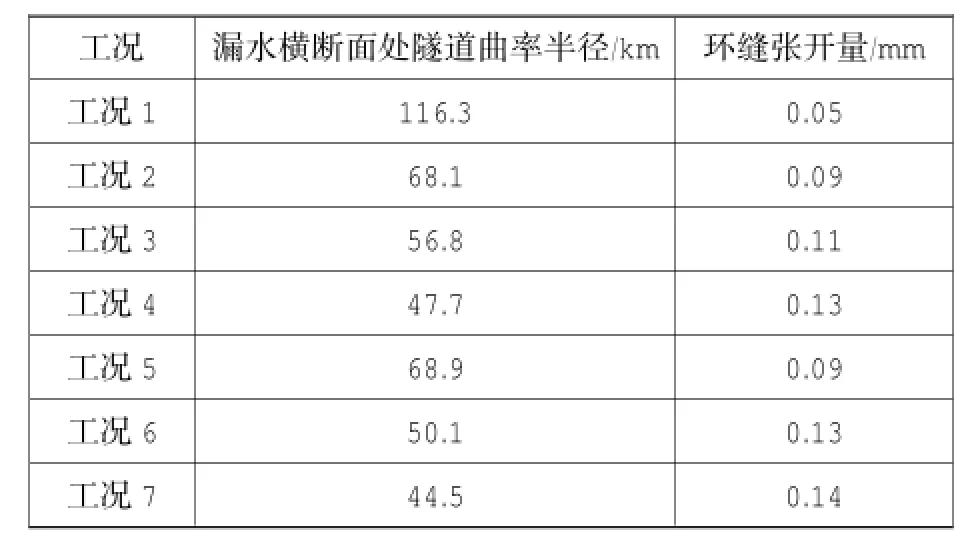
表6 不同工况下隧道曲率半径和环缝张开量Table 6 Curvature radius and joint openning of tunnelat different working conditions
假设此时隧道环缝螺栓还处于弹性状态,将表2中的隧道结构参数以及表6中漏水位置处隧道的曲率半径代入式(4)[21]中:

式中:δj为与相对应的环缝接头螺栓的最大张开量;R为纵向曲率半径;ls为环宽;x和φ分别为中性轴的位置和角度。
得到不同工况下环缝接头螺栓的最大张开量如表6所示。当隧道局部发生漏水后,隧道沉降使得隧道环缝最大张开量增大,当漏水位置越靠近隧道底部时,环缝张开量越大,当环缝张开量越大,漏水量会增加,对比工况1和工况5~7可知,漏水量增大会使得接头螺栓张开量越大,进一步恶化漏水环境,从而验证了隧道漏水与隧道变形耦合发展的机理。
3 结语
本文通过建立三维模型,分析了在灾害环境下隧道局部一环管片的不同位置发生漏水以及不同漏水量下地表沉降、隧道沉降的规律,主要结论如下:
1)由于隧道纵向刚度产生的阻碍作用,使得隧道局部漏水位置越低,地表沉降最大值越小。地表最大沉降值与漏水量成线性正比的关系,漏水量增大,地表受影响的范围也扩大,同时沉降值达到稳定所需要的时间也越久;灾害发生后72 h内地表沉降迅速发展,这段时间进行治理最为有效。
2)隧道沉降达到稳定相比地表沉降达到稳定更缓慢,且漏水位置越靠近隧道底部,漏水量越大,沉降达到稳定时间越长;漏水位置越靠近隧道底部,隧道沉降值越大,沉降值与漏水量之间成正比。
3)隧道局部漏水使得隧道纵向发生不均匀沉降,漏水位置越靠近隧道底部,环缝张开量越大,造成漏水量增大,漏水量增大,使得环缝张开量更大,隧道漏水与隧道变形之间恶化耦合发展。
[1] LIAO S M,PENG F L,SHEN S L.Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction[J]. Tunneling and Underground Space Technology,2008,23(4):241-430.
[2]白云,肖晓春,胡向东.国内外重大地下工程事故与修复技术[M].北京:中国建筑工业出版社,2012. BAIYun,XIAO Xiao-chun,HU Xiang-dong.Domestic and internationalimportantengineering accidents and repair technology[M]. Beijing:China Architecture&Building Press,2012.
[3]SHIN J H,ADDENBROOKE T I,POTTS D M.A numericalstudy of the effect of groundwater movement on long-term tunnel behaviour[J].Géotechnique,2002,52(6):391-403.
[4]刘印,张冬梅,黄宏伟.盾构隧道局部长期渗水对隧道变形及地表沉降的影响分析[J].岩土力学,2013,34(1):290-298. LIU Yin,ZHANG Dong-mei,HUANG Hong-wei.Influence of long-term partial drainage of shield tunnel on tunnel deformation and surface settlement[J].Rock and Soil Mechanics,2013,34(1): 290-298.
[5]郑刚,戴轩.灾害环境下隧道不同部位漏水对于周围土体及平行隧道的影响研究[J].岩石力学与工程学报,2015,34(S1):3 196-3 207. ZHENG Gang,DAI Xuan.Influence of different leakage positions of tunnel on surrounding soils and parallel tunnel under disaster environment[J].Chinese Journalof Rock Mechanics and Engineering,2015,34(S1):3 196-3 207.
[6]WONGSAROJ J,SOGA K,MAIR R J.Modelling of long-term ground response to tunnel ling under St James′s Park,London[J]. Géotechnique,2007,57(1):75-90.
[7] 曾东洋.盾构隧道衬砌结构力学行为及施工对环境的影响研究[D].成都:西南交通大学,2005. ZENG Dong-yang Research on the mechanical behavior of shield tunnel lining structure and influence on the environment in construction[D].Chengdu:Southwest Jiaotong University,2005.
[8]何川,苏宗贤,曾东洋.盾构隧道施工对已建平行隧道变形和附加内力的影响研究[J].岩石力学与工程学报,2007,26(10):2 063-2 069. HE Chuan,SU Zong-xian,ZENG Dong-yang.Research on influence of shield tunnel construction on deformation and secondaryinner force ofconstructed paralleltunnel[J].Chinese Journalof Rock Mechanics and Engineering,2007,26(10):2 063-2 069.
[9]钟小春,朱伟,季亚平,等.盾构衬砌管片环弯曲等效刚度的一种确定方法[J].地质与勘探,2003,39(S):185-189. ZHONG Xiao-chun,ZHU Wei,JI Ya-ping,et al.The method to confirm the effective bending stiffness of shield-driven tunnel lining[J].Geology and Prospecting,2003,39(S):185-189.
[10]黄宏伟,徐凌,严佳梁,等.盾构隧道横向刚度有效率研究[J].岩土工程学报,2006,28(1):11-18. HUANG Hong-wei,XU Ling,YAN Jia-liang,etal.Study on transverse effective rigidity ratio of shield tunnels[J].Chinese Journal of Geotechnical Engineering,2006,28(1):11-18.
[11]钟小春,张金荣,秦建设,等.盾构隧道纵向等效弯曲刚度的简化计算模型及影响因素分析[J].岩土力学,2011,32(1):132-136. ZHONG Xiao-chun,ZHANG Jin-rong,QIN Jian-she,et al.Simplified calculation modelfor longitudinal equivalent bending stiffness ofshield tunneland its influence factors′analysis[J].Rock and SoilMechanics,2011,32(1):132-136.
[12]潘海泽,黄涛,杨海静,等.运营隧道渗漏水灾害分类和等级评定方法[J].干旱区地理,2009,32(1):145-161. PAN Hai-ze,HUANG Tao,YANG Hai-jing,et a1.Classification and grading assessmentmethod ofleakage disasters in running tunnel[J].Arid Land Geography,2009,32(1):145-161.
[13]郑永来,韩文星,童琪华,等.软土地铁隧道纵向不均匀沉降导致的管片接头环缝开裂研究[J].岩石力学与工程学报,2005,24(24):4 552. ZHENG Yong-lai,HAN Wen-xing,TONG Qi-hua,eta1.Study on longitudinalcrack ofshield tunnelsegmentjointdue to asymmetric settlementin softsoil[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(24):4 552.
[14]刘印,张冬梅,黄宏伟.基于纵向不均匀沉降的盾构隧道渗漏水机理分析[J].铁道工程学报,2011(5):66-70. LIU Yin,ZHANG Dong-mei,HUANG Hong-wei.Analysis of mechanism ofwater leakage induced by longitudinaluneven settlement of shield tunnel[J].Journal of Railway Engineering Society, 2011(5):66-70.
Influence of different leakage positions of partial tunnel on tunnel deformation and surface settlement
YAO Jie1,2,DAIXuan3,ZHENG Gang1,2,SUN Jia-yu1,2
(1.Key Laboratory of CoastCivil Structure Safety of Ministry of Education,Tianjin University,Tianjin 300072,China; 2.State Key Laboratory ofHydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China; 3.Tianjin Municipal Engineering Design and Research institute,Tianjin 300051,China)
Considering the disaster caused by leakage in differentregions oflocal segment of the tunnel in water-rich area,we set up 3-dimensionalfluid-solid coupling modelto compare and analyze the ground surface settlement and tunnel deformation under different leakage positions and different leakage amount.The results indicate that the lower leakage position causes the smaller of maximum surface settlement,and the wider and shallower surface settlement troughs.With the increase of leakage, the surface settlementbecomes obvious.Local tunnel leakage will lead the tunnellongitudinaluneven settlement,enlarging the joint opening of the adjacent segments.The lower leakage position,the greater the joint opening,the open quantity is proportional to the flow.As a result,the mechanism of coupled development between leakage and deformation of tunnel is verified.
tunneling engineering;leakage positions;disaster;settlement;tunnel deformation
U654;U455.43
A
2095-7874(2017)02-0009-07
10.7640/zggwjs201702002
2016-09-26
2017-01-18
国家自然科学基金(41630641)
姚杰(1991— ),男,重庆涪陵人,硕士,主要从事隧道工程领域的科研工作。E-mail:tju_yao@163.com
