半潜式钻井平台动力定位控制器设计

王 莉，陈红卫

（江苏科技大学 电子与信息工程学院，江苏 镇江 212003）

半潜式钻井平台动力定位控制器设计

王 莉，陈红卫

（江苏科技大学 电子与信息工程学院，江苏 镇江 212003）

针对运动参数及外界环境扰动的不确定性的动力定位系统，考虑系统设计过程中的各种约束问题，本文基于广义预测控制基本理论设计了非线性预测控制器，同时将遗传算法y应用到广义预测控制器的滚动优化中，提高寻优速度。最后以981半潜式钻井平台为研究对象进行了仿真实验，仿真结果表明该控制器的有效性和优越性。

半潜式钻井平台；动力定位；广义预测控制；遗传算法

海洋结构物在海上进行作业时，需要在风、浪、流等外界环境的作用下，仍然能保持在预定的工作区域，这就需要定位系统来完成[1]。比较常见的定位方式有锚泊定位和动力定位。锚泊定位主要依靠锚链的张力提供的反力来抵抗外界风、浪、流等环境力，从而将海洋平台保持在预定的工作水域内。但随着水深增加，抛锚难度增大，成本高，定位精度受到限制。而动力定位系统是依靠推进器的推力抵抗外界环境的干扰，将海洋平台维持在预定的工作区域内。灵活性好，操作简单，定位精度高。

海洋结构物在海上的动力学特性具有强耦合、非线性、大时滞和大惯性等特点，很难建立精确的数学模型，而且外界环境的干扰也会随着不同海况发生变化，传统的PID控制已无法满足要求。模糊控制、神经网络控制、鲁棒控制等控制方法都被应用于DP控制系统。

文中基于广义预测控制理论设计了非线性预测控制器，并采用遗传算法进行优化，通过仿真实验验证该算法控制效果较好，具有较强的鲁棒性。

1 半潜式钻井平台动力定位系统的数学模型

1.1 坐标系

建立如图1所示的半潜式钻井平台坐标系统，一套是固定坐标系，另一套是随船坐标系。，两个坐标系的原点都在平台的重心处，各个坐标轴的指向如图所示。

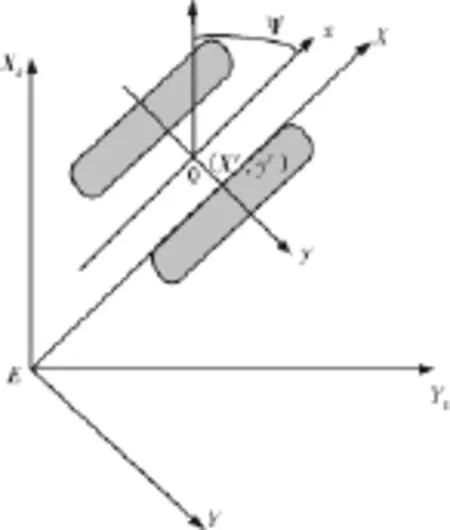
图1 平台坐标系

对于动力定位系统的半潜式钻井平台，我们只考虑其在水平面3自由度的运动，即纵荡、横荡和艏摇3个方向。我们用向量η=[x，y，ψ]T代表平台在固定坐标系下的位置和艏摇角度；取向量ν=[u，v，r]T代表平台在随船坐标系下速度，则固定坐标系和随船坐标系之间的转换关系如下：

其中：转换矩阵

1.2 平台低频运动方程

装配有动力定位系统的海洋平台，在海洋上主要受到风力、波浪力、流力、推进器的推力、以及系统的运动阻尼等共同作用。平台在风浪流作用下的运动可简化为低频运动和高频运动的叠加。动力定位系统只考虑平台的低频，低频运动方程如下：

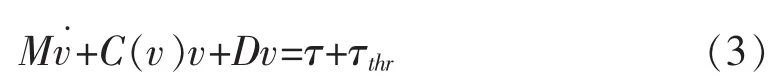
其中，M是包含附加质量的惯性矩阵，v是平台的速度向量，C（v）是科式力和向心力矩阵，D是阻尼矩阵，τ是外界环境力（风、浪、流），τth是推力器产生的推力。在动力定位系统中，平台的运动速度很小，因此C（v）v项可以忽略。

式中，质量矩阵M和阻尼矩阵D定义为：

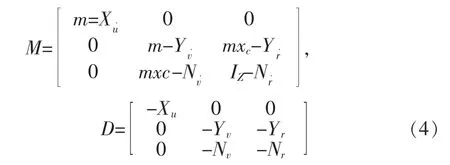
动力定位系统控制器的设计需以状态空间形式的数学模型为基础，因此，需要将上述低频线性运动模型转化为状态空间形式。在固定坐标系中的平台期望艏向角为ψd，实际艏向角为ψ。假设ψd和ψ相差不大，运用小角理论可得，非线性旋转矩阵（2）可近似表示为一个单位矩阵。由此可得平台低频运动的线性状态空间模型为：

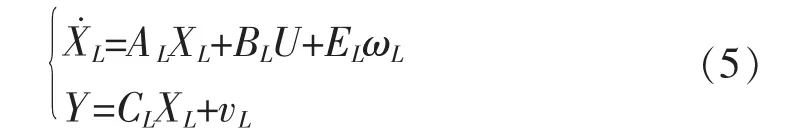
其中，XL为平台状态向量，XL=[ηT，vT]T；ωL为三维扰动向量；yL为平台位置和艏向角；vL为传感器测量的三维噪声向量，假定为高斯白噪声。各系数矩阵定义如下：

2 基于广义预测控制原理的动力定位控制器设计

对于执行动力定位的半潜式钻井平台而言，其有着不同类型的约束，在控制系统设计中必须加以考虑，如功率消耗约束、推进器负载约束、操作区和工作区约束。而广义预测控制可以很好地处理动力定位系统存在的各种约束，而且GPC具有预测功能，可以在偏差产生之前就进行校正，对系统参数及环境变化有更强的鲁棒性。基于GPC的动力定位系统框图如下：

图2 基于GPC的动力定位系统结构框图

主要工作如下：

1）建立可以预测平台未来时域行为的预测模型；

2）初始化：包括GPC的相关参数（如预测时域、控制时域、控制加权系数、输出加权系数、柔化系数等）以及平台状态空间模型的初始化；

3）定义系统的性能指标，如下所示：

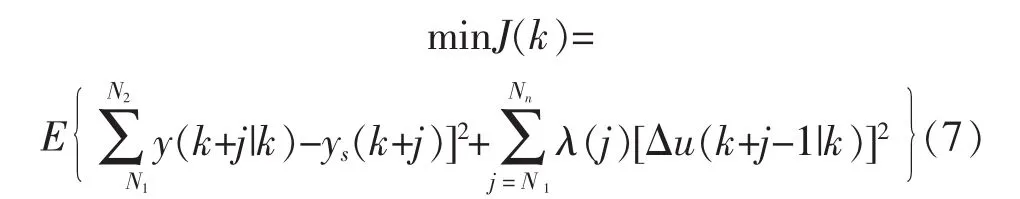
4）考虑平台动力定位系统中的约束条件（推力器约束和操作区域约束）；

5）进行滚动优化：在线求解控制向量，直至满足最优性能指标以及所有约束条件。

3 遗传算法

遗传算法是一种基于达尔文物种进化论中 “适者生存，优胜劣汰”思想的搜索最优解的方法，是一种全局概率搜索算法。遗传算法直接对研究对象进行操作，仅用适应度函数值来评估个体，采用概率变迁的规则来自动获取和指导它的搜索空间，而且可以自适应地调整搜索方向。这些特点使得遗传算法广泛应用于模式识别、图像处理、自适应控制等领域。

遗传算法的流程图如图3所示：

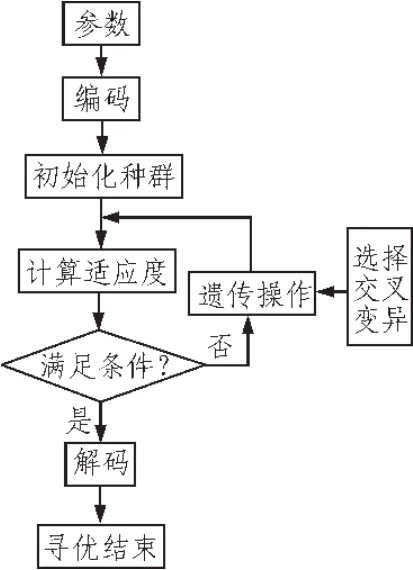
图3 遗传算法流程图

1）确定需要寻优的参数；

2）选取合适的编码方式对参数进行编码；

3）初始化：t=0，随机生成个体个数为M的原始群体P（0）；

4）适应性函数评价：分别计算种群中每个个体的适应度值；

5）遗传操作：包括选择运算、交叉运算和变异运算，确定选择算子、交叉算子和变异算子的数值；

6）终止条件判断：如果迭代次数达到设定值时，误差没有满足要求，则选择最佳适应度个体作为最优解；如果在进化过程中误差满足了要求，则选择当前的个体作为最优解，停止进化。

我们将遗传算法引入到GPC控制的滚动优化中，将控制增量Δu作为寻优变量，按照图3所示的算法流程进行寻优，直至满足所有的约束条件和性能指标，得到最优的Δu。

4 仿真实验

4.1 平台参数

文中选择981钻井平台进行仿真研究，平台主要参数见表1。

表1 平台模型参数

该平台的模型参数通过多次大规模的海试辨识得到，其中，无因次的质量矩阵和阻尼矩阵分别为：

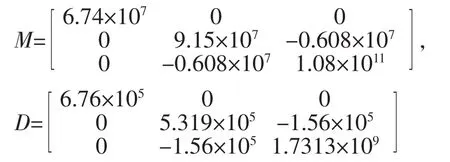
4.2 约束条件

仿真过程中所施加的约束力大小如表2、表3。

表 2 平台推力器限制

表 3 平台操作禁区

4.3 仿真结果

文中作如下假设，平台处于无风静水的仿真环境中。设平台初始位置坐标为η=[0，0，0]，给定的期望位置为η=[30，20，20]，仿真时间为1 000 s。观测经过设计控制器后，平台的位置和艏向输出值，以及控制作用的推力和力矩大小。

图4 纵荡位置输出

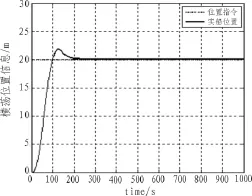
图5 横荡位置输出

图6 艏向角度输出

图7 纵向控制力输入

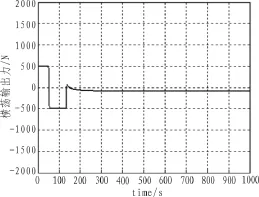
图8 横向控制力输入

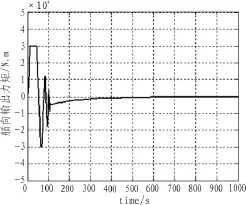
图9 艏向控制力矩输入

从仿真结果可看出，基于遗传算法的广义预测，在纵向、横向和艏摇3个方向都达到了很好的控制效果，使平台快速准确地从初始位置到达目标位置，而且可满足系统的推力器和操作区域的约束限制。

5 结 论

文中利用广义预测控制在处理约束方面的优势，设计了基于广义预测控制理论的力定位控制器，很好地解决了动力定位过程中各种约束问题，在此基础上，将遗传算法应用到广义预测控制的滚动优化中对控制变量进行优化，达到了良好的控制效果。

[1]王丽娜.船舶动力定位系统控制器的设计与仿真[D].大连：大连海事大学，2012.

[2]边信黔，付明玉，王元慧.船舶动力定位[M].北京:科学出版社，2011.

[3]齐亮，俞孟蕻.船舶动力定位系统的广义预测控制方法研究[J].中国造船，2010，51（3）：154-160.

[4]Thor I Fossen.Handbook of marine craft hydrodynamics and motion control[M].Norway:Norwegian University of Science and Technology，2011:191.

[5]苏义鑫，赵俊.基于广义预测控制的船舶动力定位约束控制[J].船舶工程，2015（3）:49-52.

[6]常佳佳，郭百巍，王星德.基于遗传算法的模型辨识[J].计算机仿真，2015，32（2）:102-105.

[7]Du J，Hu X，Liu H.Adaptive robust output feedback control for a marine dynamic positioning system based on a high-gain observer[J].IEEE Transaction on Neural Networks&Learning Systems，2015: 4554-4559.

[8]李源，补给船船位广义预测控制方法研究[D].哈尔滨：哈尔滨工程大学，2011.

[9]Mahfouf M，Linkens DA，Asbury AJ，et al.Generalized predictive control （GPC）in the operating Theatre[J].IEE Proc.D.1992，139（4）:404-420.

[10]郭琪伟，半潜式石油平台动力定位控制系统研究[D].广州：广东工业大学，2009.

[11]顾楠.船舶动力定位仿真技术研究[D].北京：中国舰船研究院，2011.

[12]Nguyen DT，Quek ST.Design of high level hy-brid controller for dynamic positioning from calm to extreme sea condition[J].Automatica.2007，5（43）: 768-785.

[13]王会丽.单点系泊下船舶动力定位控制方法研究[D].哈尔滨：哈尔滨工程大学，2012.

Design of dynamic positioning controller for semi-submersible drilling platform

WANG Li，CHEN Hong-wei
（School of Electronics and Information，Jiangsu University of Science and Technology，Zhenjiang 212003，China）

For the uncertainty of the motion parameters and the external environment disturbance of dynamic positioning system，considering all the restrictions in the process of system designing，the article designed a nonlinear predictive controller based on generalized predictive control theory.At the same time，the genetic algorithm is applied to the rolling optimization of the generalized predictive controller，which can improve the optimizing speed.Finally，simulation experiments were carried out on 981 semi-submersible drilling platform，and the simulation results show the effectiveness and superiority of the proposed controller.

semi-submersible drilling platform；dynamic positioning system；generalized predictive control；genetic algorithm

TN876.3

：A

：1674-6236（2017）02-0117-04

2016-03-30稿件编号：201603403

江苏省产学研联合创新基金——前瞻性联合研究（BY2013066-08）；江苏高校高技术船舶协同创新/江苏科技大学海洋装备研究院资助（HZ2015006）

王 莉（1989—），女，安徽马鞍山人，硕士研究生。研究方向：船舶自动化。