基于遗传算法的物流车辆派送管理

刘海燕，余世欣

（成都理工大学 工程技术学院，四川 乐山614007）

基于遗传算法的物流车辆派送管理

刘海燕，余世欣

（成都理工大学 工程技术学院，四川 乐山614007）

为了提高物流车辆的运营效率和节约其成本，分析与描述了多车辆同时服务于多城市的配送模式，然后建立了4辆车配送50个城市的运输总路程模型，接着利用遗传算法的优化技术对运行路线进行最优性的规划。仿真结果表明：遗传算法经过3712次的迭代获得最优解，50个城市分别有且只有1辆车经过，4辆车的最短总路程为812.1628公里。

配送模式；总路程模型；遗传算法；优化；最短路程

随着电子商务技术发展的日新月异，物流行业自身管理与运营的水平的提高也需要顺势而为，否则这块“短板”将会制约电子商务行业整体的发展。对于物流行业，高效率是其管理的核心宗旨，而运营成本的最小化是反映管理水平的重要指标。提高交通运输工具以及行驶线路等方面的作业水平都会对物流费用产生积极性影响[1]，因此合理规划与管理车辆行驶路线可以有效降低运营成本。可以采用计算离散客户之间的节约值和运用EXCEL2000中的规划求解最佳路径两种方法来规划行驶线路[2]。该方法需要通过表格数据运算处理，较为繁琐；利用GIS（地理信息系统）技术使得企业随时可以查看任何区域的电子地图，从而得到有效的路径规划[3]，该方法相当于提供电子地图，而对多个目的地址的路线不能进行有效规划；还可以采用遗传算法进行车辆路径规划[4]，而该文献假设的模型只有一个中心站点，整个区域内只有1辆货车运行。文中先针对多车辆、多节点的运行路线模式进行描述分析，然后建立50个独立城市、4辆车共同派送的物流配送模型，最后在遗传算法的理论基础之上对运行路线进行优化选择。结果表明：遗传算法经过3712次的迭代获得最优解，其最短总路程为812.1628公里。

1 运行路线模式分析

已知物流公司设定某一固定集散点中心，自身拥有N辆车，专门为M个固定位置的城市配送货物（M＞N），那么物流公司管理人员面临的问题就是：如何规划N辆车进行物流配送的路线，使得每一个城市目的地均有且只有1辆车到达送货，而且所有车辆完成各个城市的配送任务所往返的路程总和要最短。所以该情况不是一个简单的电子地图问题，而是一个数值优化问题。对于多辆汽车共同配送的情况，可以按照一定的分解策略把整个过程看成多个单辆汽车的配送路径优化问题，这样只要找到每辆汽车的最优配送路径以后，然后根据相应的原则再来求和，最后就能得到整个物流配送过程的最优配送路径规划。下面需要先建立问题的数学模型，然后采用遗传算法进行优化处理。

2 模型的假设与建立

假定已知物流公司设定的固定集散点中心平面坐标为（X，Y）=（64，8），自身拥有N=4辆车，专门为M=50个固定位置的城市配送货物，这50个固定位置的城市平面坐标如表1和表2所示。

表1 前25个城市平面坐标

表2 后25个城市平面坐标

由于我们需要每一个城市目的地均有且只有1辆车到达送货，这里把各个城市与车辆的之间的配送情况用变量Pij表示，其下标i代表第i辆车；下标j代表第j个城市。变量Pij取值如式（1）:

再根据各个城市相互之间的地理坐标数据，表示各个车辆的运输路径之和（即优化目标函数）为式（2）：

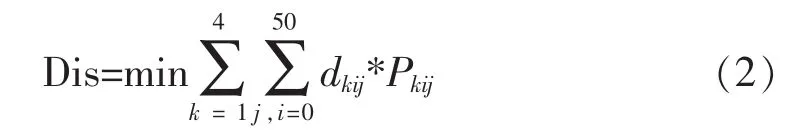
在式（2）中，dkij代表第k辆车经过两个相邻城市i、j之间的距离，而代表各个城市与车辆之间配送情况的变量Pkij有4组取值：P1ij、P2ij、P3ij、P4ij；这4组中的组合变量ij取值要各不相同。根据表1和表2的坐标数据采用遗传算法进行求解最佳优化结果。

3 遗传算法及其优化过程

遗传算法原理来源于生物进化原理的灵感，它是一种全局搜索算法，其求解问题的基本思路为：把待求解的问题变量表示成“染色体”，变量的多个取值就构成一群染色体，把多个不同的“染色体”变量置于问题的“环境中”，根据适者生存、优胜劣汰的生物进化原则，在这些“染色体”中选择适应度较高的染色体进行复制，再通过交叉和变异产生出下一代适应度更高的染色体；如此反复循环，经过若干次数的迭代，最终收敛到一个最高适应度的个体上，也就得到问题的最佳优化结果[5]。遗传算法的特点[6]主要有以下几点：

1）传统搜索算法是从单个初始值进行迭代搜索最优解，这样容易产生过早收敛。而遗传算法从问题解的串集开始搜索，避免“早熟现象”带来的局部最优解问题。

2）遗传算法并行处理染色体中的不同个体基因，也就是在整个搜索空间里对所有解进行适应度计算，降低出现局部最优解的优化结果。

3）遗传算法只是采用适应度函数值来选择代遗传的个体进行优化求解，不需要增加额外的搜索空间知识或其它辅助信息。由于适应度函数的定义域可以不受限制，也不会受连续可微的约束性。鉴于此因，遗传算法的应用领域较为广泛。

4）遗传算法依据概率的可变规则来引领它的搜索方向，也就是说它是非确定性的。

5）遗传算法具有自重组、自适应和自学习的3大特点。它利用求解的迭代过程中获得的信息自行组织搜索时，适应度值较大的基因个体具有较高的遗传到下一代的概率，并重新形成适应度更高的个体结构。优化过程如图1所示。

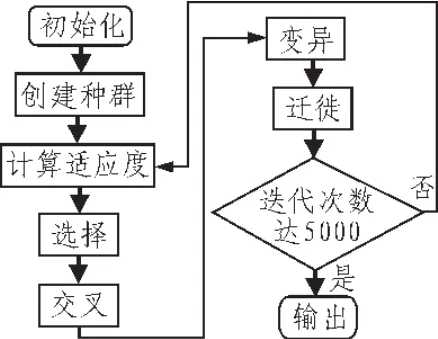
图1 优化过程

在图1的步骤中，首先进行初始化，将表1、表2的50个城市地理坐标信息加载进来，然后创建包含40个个体的种群，每个个体包含两个变量值，分别表示两个城市的序号组合与是否经过该相邻城市；这样利用其值计算适应度，并根据适应度高（总距离最短）的染色体选出来进行交叉、变异、迁徙，然后重新计算适应度值，迭代完5 000次以后，输出最优解。

4 仿真分析结果

先把各个已知城市的坐标数据录入文本文档，以供程序初始化时采用load指令加载调用，根据建立的数学模型和遗传算法流程，编写MATLAB试验程序，验证其设计的效果。

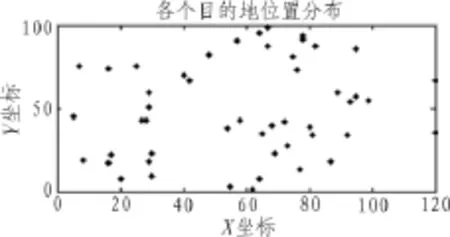
图2 城市分布图

根据表1和表2的坐标数据绘制成各个被配送城市的平面分布图如图2所示，可以看出：Y坐标方向的最大距离差在100公里左右，X坐标方向的最大距离差在120公里左右，4辆车负责完成这50个分布城市的非重复性配送任务，并返回物流公司的集散中心。

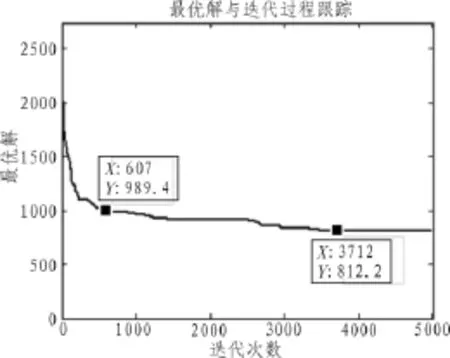
图3 迭代运算过程

图3 是通过遗传算法优化路线时总距离最优解随着迭代次数的变化过程跟踪，可以看出：总距离由一个较大的距离数值开始急剧下降，前1段迭代过程中的收敛速度较快，然而在第607次迭代左右得到一个局部较优解，不过随着迭代次数的增加，总距离的较优解依然在变化，也就是该遗传算法既较好地避免了过早收敛的问题，也具备较快的收敛速度。最终在第3712次迭代处取得最优解，即最小总路程数为812.2公里。

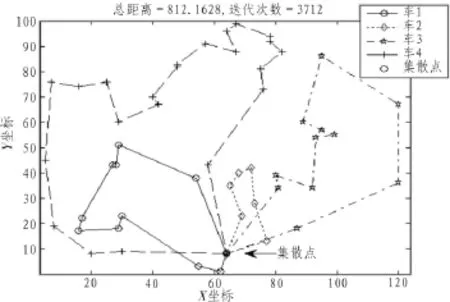
图4 最佳路线图

通过遗传算法优化求解得到的4辆车配送路线图如图4所示。在图4中，4辆物流车从集散点出发，分别沿着4条不同的线路对50个独立城市进行配送，各个城市被完全覆盖，而且只有1辆车经过，最远路程的是第4辆车，最近路程是第2辆车，统计出4辆车的总路程为812.1628公里，相应的迭代次数为3712次，其值与图3的最优迭代解相吻合。

5 结束语

文中从降低物流车辆运营成本的角度出发，分析与描述了多车辆共同派送于多城市的运行路线模式，然后建立了相应的物流配送模型，接着利用遗传算法的优化技术对运行路线进行最优性的规划选择，仿真结果表明：4辆车分别沿着4条不同的线路完成50个城市的配送任务，各个城市有且只有1辆车经过，4辆车的总路程为812.1628公里。

[1]王晶.浅谈电子商务环境下企业物流管理的方法[J].现代商业，2014（26）:127-128.

[2]易华平，浅谈两种配送路线求解方法的比较[J].商场现代化，2007.12，（524）:110-111

[3]王钰，物流信息技术管理方法研究[J].数字技术与应用，2015（10）:80-80

[4]付瑞，张纪会.基于遗传算法的电子商务物流配送研究[J].青岛大学学报（工程技术版），2015，30（1）:81-86

[5]陈同英，遗传算法在林木采伐作业信息管理中的应用[J].运筹与管理，2001，10（4）：96-101

[6]百度百科，遗传算法[EB/OL].http://baike.baidu. com/linkurl=BTbVRoxHmTNjVe7DJFPHsXoJDb 3R4TrvfvgvmWyuGH4gMlp6oz0IqhrjWF7KyEAtdF dCCqkdAx4QKBcwec2ziK.

Management for delivery of logistics vehicle based on genetic algorithm

LIU Hai-yan，YU Shi-xin
（College of Engineering and Technology，Chengdu University of Technology，Leshan 614007，China）

In order to improve the logistics vehicle operating efficiency and save the cost，analysis and describes the distribution pattern of multiple vehicles at the same time in the service of the multiple cities，then sets up the distribution model of the total transportation distance of 4 cars which distribute for 50 cities，then plans the running routes by using the genetic algorithm's optimization technique.The simulation results shows that Genetic algorithm （ga）obtains the optimal solution after 3712 times iterations，50 cities have respectively only 1 car by passing，and the shortest total distance of 4 cars passing is 812.1628 km.

distribution mode；the total distance model；genetic algorithm；optimization；the shortest distance

TN0

：A

：1674-6236（2017）02-0037-03

2016-01-27稿件编号：201601248

刘海燕（1979—），女，吉林长春人，硕士，讲师。研究方向：信息管理、物流管理等相关的教学与科研。