EGM2008模型在GPS高程转换中的适用性探讨

路媛琦，章传银，李圳

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590； 2.中国测绘科学研究院，北京 100039)

EGM2008模型在GPS高程转换中的适用性探讨

路媛琦1*，章传银2，李圳1

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590； 2.中国测绘科学研究院，北京 100039)

传统高程测量方法在地形复杂地区和已知水准点较少的情况下难以实施高程控制测量。本文提出了利用GPS获得的大地高与EGM2008模型结合获取高程异常值，从而通过GPS获取的大地高和高程异常值拟合求出控制点正常高的方法，经在不同测区验证表明，此方法可以达到四等水准测量的精度，提高了高程控制测量的效率。

EGM2008模型；高程异常；GPS高程拟合

1 引 言

传统的高程测量方法主要是水准测量和三角高程测量，测量程序复杂，工作效率比较低，在地形复杂和范围较大的测区费时费力，高程测量的进度往往要落后于平面控制测量，高程测量直接影响项目的总体进度，为后续的测量工作带来了不便。全球定位系统(Global Positioning System，GPS)技术可以很容易获得点位厘米级甚至毫米级的三维坐标，因此GPS技术给高程测量带来了新的获取方式，但是利用GPS测量获得的高程是在WGS-84(World Geodetic System-1984 Coordinate System)坐标系中的大地高，而我国采用的是正常高，因此GPS测量得到的高程不能直接应用于项目生产。一点的正常高即用该点的大地高减去该点相应的高程异常值即可以得到，如果知道高程异常值后就可以将大地高转化为正常高，因此高程异常值的获取十分关键。

求解高程异常的方法有重力法、GPS水准法、联合平差法、转换参数法、神经网络等方法。其中GPS水准法是普遍，也是最容易实现的方法之一。GPS水准法是利用测区内已知高程异常的已知点，采用比较适宜的模型对该测区的似大地水准面进行拟合，然后求出待定点的高程异常值，从而确定整个测区的正常高。目前常用的GPS水准方法主要分为曲线拟合法和曲面拟合法。曲线拟合主要有多项式曲线、三次样条曲线等方法。曲面拟合主要有相关平面、斜平面、多项式曲面、多面函数、曲面样条、移动曲面等[1-3]。利用GPS进行高程拟合的优点是算法相对来说比较简单，不受中、长波项及高程系统异常等的影响，无须地球重力场方面的专业知识和数据，缺点是在山区精度会受到损失。而且利用GPS进行高程拟合需要一定数量、分布合理、且能均匀覆盖整个拟合区域的GPS点，从而用这种方法求解高程异常值的工作量比较大，并且在水准点稀少的测区实施起来比较困难。本文使用少量水准点基于EGM2008模型实现GPS大地高到正常高的转换。

2 基于EGM2008的高程拟合

2.1 基于EGM2008的高程拟合及精度

地球重力场模型(Earth Gravitational Model 2008，EGM2008)是美国国家地理空间情报局(National Geospatial-Intelligence Agency，NGA)在2008年推出的新一代全球重力场模型。该模型是NGA经过多年的探究和整理，在以往建立的地球重力模型的理论与实践的基础上，采用领先的建模方法和技术完成的地球重力场模型[4，5]。EGM2008模型提供的最终成果包括： 2 190阶次的全球重力场模型；全球5′×5′空间分辨率的重力异常；全球5′×5′、2.5′×2.5′、1′×1′网格大地水准面；全球5′×5′网格垂线偏差[6]。

章传银等学者对EGM2008模型在我国大陆的适用性进行了研究，研究结果表明：EGM2008模型高程异常在我国大陆的总体精度为 20 cm，华北地区 9 cm，华东华中地区 12 cm，西部地区为 24 cm；EGM2008模型空间异常在我国大陆的总体精度为 0.010 5 cm/s2[7]。

(1)

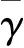
综上所述，高程异常的表达式为：

ζ=ζGM+ζ△G+ζT

(2)

式(2)中，ζGM为长波因素，可以由地球重力场模型计算出；ζ△G为中波因素，由重力场异常边值的求解得到；ζT为短波因素，由地球改正的解得到。综上所述，ζGM可以由EGM2008模型重力场中的长波信息求得，ζ△G和ζT可以由GPS高程测量中已知正常高的控制点逼近，利用已有数学模型拟合出未知点位的ζ△G和ζT两项值[9]。

GPS所测量得到的是大地高，而我国采用的是正常高系统，大地高与正常高之间的关系：

h=H-ζ

(3)

式(3)中，h为正常高；H为大地高；ζ为高程异常值；

由于我国所采用的似大地水准面于EGM2008所采用的似大地水准面之间存在一个差值，而这个值是在实际项目计算中必须考虑这一个差值，故式(3)又可表示为：

h=H-(ζi+△ζ)

(4)

式(4)中，h为正常高；H为大地高；ζi为EGM2008模型计算这个点的高程异常值；△ζ为模型差即EGM2008似大地水准面与我国采用的似大地水准面之间的差值；

若已知控制点正常高，用GPS测量出控制点在WGS-84参考椭球面上的大地高，由大地高与正常高之间的关系，求出控制点的高程异常值，再利用EGM2008模型计算出该控制点在EGM2008全球似大地水准面与WGS-84参考椭球面之间的高程异常值，根据式(3)和式(4)即可得到EGM2008全球似大地水准面与我国采用的似大地水准面之间高程异常值差值，即：

△ζ=H-h-ζi

(5)

式(5)中，h为正常高；H为大地高；ζi为EGM2008模型计算这个点的高程异常值；△ζ为模型差即EGM2008似大地水准面与我国采用的似大地水准面之间的差值；

由于在地区重力场的半波长范围内，模型误差具有很强的相关性，因此可以用该控制点上求出的高程异常值差值，近似代替半波长范围内的所有差值，然后求出该测区各个控制点在EGM2008模型下的高程异常值和测量出各控制点在WGS-84参考椭球面上的大地高，从而求出各控制点在我国高程基准下的高程即：

hi=Hi-(ζi+△ζ)

(6)

式(6)中，hi为各个点正常高；Hi为各个点大地高；ζi是EGM2008模型计算各个点的高程异常值；△ζ为模型差即EGM2008似大地水准面与我国采用的似大地水准面之间的差值；

基于EGM2008模型的GPS高程拟合得到控制点的正常高，需要进行精度评定。为了客观评价得到正常高的精度，应在测区有几何水准联测点且尽量多的联测GPS高程点，且最好均匀分布整个测区，以便做外部检核。可以将EGM2008模型拟合高程的精度误差来源分为三个方面：GPS测量大地高的精度、仪器高的量取和EGM2008模型分辨率及精度。

现在GPS接收机可以得到厘米甚至毫米级的大地高，而在GPS测量中仪器高的量取至关重要，量取仪器高的精度影响着最终成果的高度，合适的仪器高量取方法也是提高测量精度的方法之一，而在类似Trimble、Leica等GPS静态接收机在量取仪器高方面有较高精度，仪器高的量取误差不会超过 2 mm。张兴福等根据三个测区的GPS高程控制网水准数据，利用水准点检核和高差检核的方法来计算EGM2008模型的精度得到的成果显示：利用EGM2008模型求出的水准点的高程异常差将大地高转换为正常高的精度平均为 0.2 cm，均方误差为 ±4.5 cm[10]。

2.2 实例计算分析

本文结合西部某水利工程测图控制网工程测量项目，对基于EGM2008模型的GPS高程拟合在工程测量项目中的可行性检验和对比分析。选取的工程项目控制线性地形长度约为 60 km，测区内最高海拔约为 520 m，最低处海拔约为 488 m。利用GPS在测区建立E级GPS控制网，均匀布设23个E级GPS控制点，将已知3个省测绘局布设的GPS C级控制点作为起算点；同期测量四等水准测量；测区内已知2个三等水准点，位于测区两端；水准实测结果满足规范要求，经过严密平差得到各控制点水准高程。

(1)两种高程拟合方案对比分析

为了更好地检验分析在已知控制点少的情况下基于EGM2008模型的GPS高程拟合的优越性，采用两种方案得出的2组高程数据与水准测量得到高程进行对比分析使检验和对比分析更加具有代表性。2种方案如下：

方案1：利用已知控制点高程异常采用平面相关法拟合高程[3]；

方案2：基于EGM2008地球重力场模型的高程拟合。

在此次实验中，用测区两端已知三等水准点求△ζ，然后向测区中心各辐射12个控制点(文中仅列出以一个三等水准点求得△ζ拟合出的控制点)，两种计算高程之间相互对比，并进行精度评定，精度评定的公式为；

(7)

式(7)中，μ为中误差；v为残差；n为参与计算点数。

方案1拟合方法为常用方案在此不再论述，在使用方案2进行拟合高程时，先将各控制点的84经纬度转换为十进制(如表1所示)，用EGM2008的1′×1′大地水准面模型计算器Alltrans EGM2008 Calculator 1.2求出各点的模型高程异常值，如表2所示。

部分控制点成果表 表1

模型计算器计算各点模型高程异常值 表2

由二等水准点A的WGS84高和水准高，由式(5)求得EGM2008似大地水准面与我国采用的似大地水准面之间的差值△ζ。

△ζ=519.706 m-571.747 m-(-52.373 m) =0.332 m

由于各个地方的WGS-84坐标不同，由WGS-84经纬度计算的模型高程异常也就不同，因此△ζ各不相同，也就是说各个测区有不同的△ζ。至此得到模型差即可由式(6)求出各个点的85高程。这样，即可以完成基于EGM2008模型的GPS高程转换。

在该项目中，采用方案1拟合出的高程，求得中误差为 2.4 cm；利用方案2拟合出的高程，求得中误差为 1.4 cm。可见在工程测量项目中，采用基于EGM2008模型的GPS高程拟合的方案2的精度比用平面相关法拟合高程的方案1精度提高了 10 mm，由此可见，基于EGM2008模型进行GPS高程拟合精度要较好。两种高程拟合方案拟合精度比较如图1所示。

图1 两种拟合方案高程拟合残差比较

(1)基于EGM2008模型的高程拟合精度

通过上表中可以知道在已知点较少的情况下虽然EGM2008模型进行GPS高程拟合结果优于平面相关法，但此结果并不代表基于EGM2008模型的GPS高程转换方法的精度。下面对水准测量与基于EGM2008模型的GPS高程拟合获得的高程进行分析。

GPS高程及水准高程之差及精度统计 表3

在表3中距离是三等点A与其他点的直线距离，而常规水准测量的距离肯定比表中的距离大。水准点高程中误差为水准测量各水准点的中误差，计算参考《数字测图原理与方法》[12]。通过比较可以看出高程差、水准点高程中误差与高程拟合精度比较接近，在一定的数量级内，基于EGM2008模型的GPS高程拟合得到的高程其精度达到四等水准限差的要求。

3 结 论

在测量项目生产中，就基于EGM2008模型进行高程拟合求得的高程数据、GPS多项式拟合和传统几何水准测量求得的高程数据相互之间进行一些比较，得到一些结论：

(1)基于EGM2008模型的高程拟合在某一测区只需少量已知水准点即可，在某一段或某一测区中只需1个高等级的已知水准点即可实现GPS所测量的大地高转化为项目需要的正常高，且对于已知点的位置要求不太高。

(2)对于已知水准点少、测区联测困难、交通不便等实施几何水准困难的测区通过EGM2008模型拟合高程有效减小了作业强度，提高了作业效率，有较强的现实意义。

(3)基于EGM2008模型的拟合高程能够达到四等几何水准的精度；利用EGM2008模型拟合高程，所得到的精度均匀且实施起来简便快捷，提高了项目整体工作效率。

(4)在已知水准点的测区，可以利用多余已知水准点高程相互检验EGM2008模型拟合高程的错误或者粗差，提高数据可靠性。

(5)对于大区域和长距离控制网中利用EGM2008模型进行高程拟合可以分区域和分段来处理，这样精度可以得到有效保证。

[1] 徐绍铨，张华海，杨志强等. GPS测量原理及应用[M]. 武汉：武汉大学出版社，2008：168～178.

[2] 杨江波，李为乐，余代俊等. GPS高程拟合方法的实验研究[J]. 测绘科学，2009，34(3)：54～57.

[3] 崔卫磊. GPS水准中三种曲面拟合模型的对比分析[J]. 城市勘测，2015(1)：85～88.

[4] 江滔. 基于EGM2008模型的GPS高程拟合方法在铁路勘测中的应用研究[J]. 铁道勘察，2013(2)：16～18.

[5] 张建恩，刘亚宁，祁钰等. EGM2008大地水准面模型在陕甘宁盆地GPS高程转换中的适应性探讨[J]. 物探装备，20133，23(2)：121～124.

[6] 杨金玉，张训华，张菲菲等. EGM2008地球重力模型数据在中国大陆地区的精度分析[J]. 地球物理学进展，2012，72(4)：1298～1306.

[7] 章传银，郭春喜，陈俊勇. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报，2009，38(4)：283～289.[8] 祝乃龙，胡景海. GPS测量高程拟合精度探讨[J]. 地理空间信息，2009，7(4)：13～15.

[9] 朱亚光，高兴国、刘炎雄等. 基于EGM2008重力场模型的高程联测方法[J]. 济南大学学报·自然科学，2011，25(4)：410～413.

[10] 张兴福，刘成，王国辉等. 基于EGM2008重力场模型的GPS高程转换方法及精度分析[J]. 地球物理学进展，2012，27(1)：38～44.

[11] GB/T12898-2009. 国家三、四等水准测量规范[S].

[12] 潘正风，杨正尧. 程效军等.数字测图原理与方法[M]. 武汉：武汉大学出版社，2008：213～218.

EGM2008 Applicability of the GPS Height Transformation

Lu Yuanqi1，Zhang Chuanyin2，Li Zhen1

(1.College of Geomatics，Shandong University of Science and Technology，Qingdao 266590，China； 2.Chinese Academy of Surveying & Mapping，Beijing 100039，China)

The conventional height measurement method cannot be applied in height control surveying of complicated areas with less already known benchmarks. This paper proposed a method combing GPS-derived geodetic height with EGM2008 to retrieve height anomaly，which is used in the simulation with GPS-derived geodetic height to retrieve the normal height of control point. Tests in different areas indicated that four-level accuracy could be reached by using this method which could also raise the efficiency of height control surveying.

EGM2008 model；height anomaly；GPS height fitting

1672-8262(2017)01-91-05

P224

A

2016—06—27 作者简介：路媛琦(1992—)，女，硕士研究生，主要从事卫星定位与导航技术的研究。