论“非精确但严密”的科学——以几何学为线索

陶建文

(华南理工大学 科学技术哲学研究中心， 广东 广州 510640)

论“非精确但严密”的科学
——以几何学为线索

陶建文

(华南理工大学 科学技术哲学研究中心， 广东 广州 510640)

胡塞尔在其后期哲学中提出一种非精确形式的原几何学的思想， 这一思想被德勒兹发展为“非精确但严密”的科学理念。 其思维的核心在于从那种外在的、 固定的、 精确的、 均匀的人造框架模式中走出来， 从而走入一种内在的、 游动的、 无定向的差异过程中去。 这种科学具有边界的模糊性， 内部结构的严密性， 可广泛用于生物学、 材料学以及空间设计等研究领域。 关键词: 非精确但严密； 平滑空间； 质料

自从胡塞尔出版其著作《几何学的起源》以来， 围绕“非精确的形式”产生了许多哲学上的思考， 如德里达在《胡塞尔几何学的起源引论》中进行过详细的探讨， 德勒兹在《千高原》中把胡塞尔的“非精确的形式”改造为“非精确但严密(anexact yet rigorous)”的科学， 即指虽然没有数学的精确性但却有构成上的严密性的科学。 德勒兹的理论被德兰达(Manuel Delanda)用来论述强度科学(intensive science)， 也被当代建筑学家林恩(Greg Lynn)用来构造一种新的可能性的建筑空间。 本文试图展示“非精确但严密”科学这一论题的基本思想。

一、 “非精确的形式”与“原几何学”

胡塞尔最早是在《纯粹现象学通论》中讨论“描述科学”与“精确科学”的区别时论及精确科学的问题的， 奇怪的是， 胡塞尔不是针对与数有关的算术来讨论精确性问题， 而是针对几何学来讨论精确性问题， 而且在他的著作中是一以贯之的这样， 这大概是因为从阿基米德到牛顿的数学化科学传统几乎是几何学化科学传统所致。

虽然几何学(geometry)本来就有土地测量的含义， 但是几何学与土地测量是有区别的。 亚里士多德曾经对几何学与测量做过区分， 几何学的对象是不可肉眼感知的， 例如一条直线与一个圆相切， 在几何学理论上它们相切于一个点， 但是在感性经验中， 无论作图怎样精密， 其相交部分都只是一个线段或一段圆弧， 而不是一个点。 这样， 直线与圆相切的“切点”只能存在于观念世界之中。 然而， 测量处理的对象是可感知的对象， 如山脉、 河流、 田地等， 都是一些感知对象， 在其中根本找不到真正的点、 直线和圆之类的东西。 既然测量的对象不同于几何学的对象， 那么依据其对象来划分的科学也就要分为两类， 这样就要把数学与以测量为基础的物理学或自然科学区分开来。 “亚里士多德确信， 数学与自然哲学或物理学之间存在着差异。 根据他的定义， 物理学把所有自然物都看成可感、 可变的物体。 而数学家则去除物体的所有可感性质， 专注于剩余的数学部分。 因此， 数学家只关注物体的几何性质， 而这些几何性质根本没有穷尽实在。”[1]胡塞尔对精确性的讨论实际上与亚里士多德关于数学与自然科学的划分相类似。

胡塞尔把精确的形式定义为可以还原为具有明见性的观念， 即只有在主观世界中才存在的东西。 “几何学概念是‘观念的’概念， 表达着某种不能被‘看’的东西……精确的概念有其本质的相关物， 后者有康德意义上的‘观念’的特性。”[2]180因此， 理论几何学的研究方向不是将它根植于直接经验到的实际对象， 而是仅仅涉及那些被设定为存在于完全精确的观念领域中的对象， 如没有部分的“点”， 没有宽度的“线”， 没有厚度的“面”等等。 而且从这些基本的观念对象可以通过逻辑演绎推广到一个无限的观念领域， 典型的例子就是欧几里得几何学体系中的公理演绎体系， 如《几何原本》中的第一个命题：已知一条线段可以作一个等边三角形。 其构造过程如下：

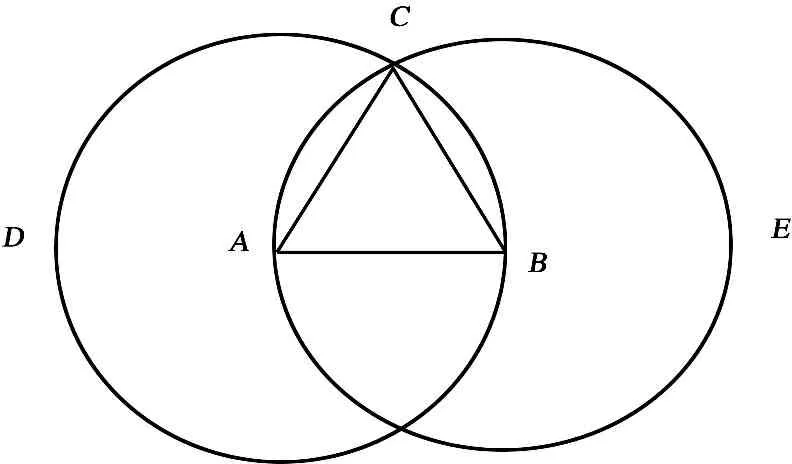
图1

设AB为已知线段， 要求以线段AB为边构造一个等边三角形。 以A为圆心AB、 为半径作圆BCD； 再以B为圆心、BA为半径作圆ACE； 两圆相交于C点， 连接CA、CB。 因为A点是圆CBD的圆心， 故AC=AB； 又因为B是圆ACE的圆心， 故BC=BA； 所以AC=BC=AB， 即三角形ABC是等边三角形。

该命题之所以成为“几何原本”中的第一个命题， 主要是等边三角形是从“点”“线”这些最原初的几何学定义即可推演构造出来的一个几何学对象， 只要最原初定义的“点”“线”概念的含义具有永恒性， 那么由上述明见性操作所得出的“等边三角形”的含义也就具有永恒性。 胡塞尔说：“借助于这些事先挑选出来的作为可资普遍利用的优越的基本成分， 按照与这些基本成分结合在一起的操作程序， 不仅构成越来越多的因其进行制作的方法而成为主观性地一义性地被规定的形状。 最终这样的一种可能性产生出来了：通过一种先天的， 包罗万象的系统的方法， 构成地， 一义性地制作出一切可设想的观念的形状。”[3]37那些观念的形状都可以在观念的逻辑网络中得到精确的界定。

与精确的观念之间的关系相对的是“非精确的形式”， 非精确形式的几何图形被描述为那样的图形， 它们没有常规固定的形状， 如圆、 三角形、 正方形或椭圆等等， 也不能还原为基本的几何学元素如“点”“线”等清晰的观念之间的关系， 其轮廓是不可精确描述的。 用它们来表征自然就属于描述的自然科学。 胡塞尔说：“我们首先考察几何学和描述的自然科学之间的对立。 几何学家不像从事描述的自然科学家那样关心事实上的感性直观形状。”[2]179-180描述的自然科学家使用一些与精确的几何学形状不同的术语来描述直接感知到的自然形状， 如百度词条对水蛭的描述：“呈扁平纺锤形， 有多数环节， 长4～10cm， 宽0.5～2cm。 背部黑褐色或黑棕色， 稍隆起， 用水浸后， 可见黑色斑点排成5条纵纹； 腹面平坦， 棕黄色。 两侧棕黄色， 前端略尖， 后端钝圆， 两端各具1吸盘， 前吸盘不显著， 后吸盘较大。 质脆， 易折断， 断面胶质状。 气微腥。”这段话用一些非标准几何学观念化的形态如“纺锤形”“环节”“隆起”“钝圆”等把水蛭的形象清晰地呈现出来。 描述中虽然有数据， 但这些数据之间没有像几何学观念之间严格的逻辑网络关系， 所以也是非精确的。 作为描述， 我们知道它也是非常严密的， 这些形态类型是根据感性直观而被直接把握的， 它们尽管模糊不清， 却是在概念上和术语上已被确定的， 借此描述我们能够把水蛭与其他各种动物区分开来， 因为它描述了这类动物的基本形态特征。 那些形态学概念具有模糊性， 但这种模糊性刚好使得它们的应用范围富于流动性， 这并非是它们的欠缺， 因为“在它们被使用的知识范围内， 它们是绝对必不可少的概念， 或者说在那些范围内它们是唯一合法的概念……最完善的几何学和最完善的对几何学的实际掌握， 不可能有助于进行描述的自然科学家去直接表达(以精确的几何学概念)， 他以简单的， 可理解的和完全适当的方式用‘齿形的’、 ‘凹形的’、 ‘透镜形的’、 ‘伞形的’诸词所表示的东西——这些简单概念在本质上而非偶然地是不精确的， 因而也是非数学的”[2]180。 可见， 胡塞尔的“非精确形式”并非是偶然不精确的， 例如测量的误差或计算的错误所造成的不精确性， 所以是一种非数学因素造成的不确定性。

非精确的形式对于动物学家、 地质学家或者今天时髦语言所说的博物学家从事描述而言是非常严密的。 与之相反， 如果博物学家们采取精确的几何学观念来研究动物的形态反而是不适合的， 因为抽象的几何学观念与感性材料完全相分离， 非精确的几何学形态却与感性材料严密地结合在一起。 这种非精确形式的几何学本身实际上是一种原初的几何学， 它描述的不是观念化的几何学本质， 而是被感官直接把握的形态学本质。 胡塞尔论几何学的起源时就是从原-几何学入手进行描述的。 “原几何学家总已利用了非精确的时空形态和本质上‘模糊的’形态学类型， 因为它们总是能够产生前几何学的描述性学科。”[4]原-几何学在它们被还原为异常清晰的陈述之前被用于描述各种外形的轮廓， 这些描述是严密的， 它们也抵制被还原为观念化的精确的形式， 从而被归为“非精确性”的范畴。

二、 非精确但严密几何学的游牧性和内蕴性

德勒兹在《千高原》中依据胡塞尔的原-几何学理论首次提到“非精确但严密”的科学：

胡塞尔曾谈到一种原-几何学(proto-geometrie)， 它研究的是那些模糊的——也即飘忽不定的或游牧的——形态学的本质。 这些本质有别于感性的物， 但同样也有别于理念的、 王权的、 帝国的本质。 作为研究它们的科学， 原-几何学自身就是模糊的， ——就“飘忽不定”(vagabonde)的词源意义而言：它既不像可感事物那般不精确， 也不像理念性本质那样精确， 相反， 它是非-精确的(anexacte)， 但却是严格的(rigoureux)(“此种不精确是本质上的、 而非偶然的”)。 圆是一种有机的、 理念的、 固定的本质， 但圆形(rond)却是一种模糊的和流动的本质， 它既有别于圆、 也有别于圆形物(一个花瓶， 一个车轮， 一个太阳……)。 一个定理性的图形是一种固定的本质， 但它的转化、 变形、 切除或扩张， 它的所有的流变， 形成了模糊的但却是严格的问题性的图形， 呈现为“透镜形”、 “伞形”或“锯齿形”。[5]527-528

从德勒兹的描述看来， 他承接了胡塞尔的“原-几何学”的思想， 认为像胡塞尔的这种原-几何学的性质， 既不是“精确(exact)”的， 也不是“不精确(inexact)”的， 而是“非精确但严密(inexact yet rigorous)”。 德勒兹举的例子是“圆”， 几何学观念上的“圆”， 即“同一平面中到一个定点的具有相同距离的点的集合”， 它是精确的； 但是像花瓶、 太阳和车轮的“圆形”却是“非精确但严密”的几何学图形。 因此， 德勒兹定义了三种几何平面图形：精确的几何， 它们与规则和严肃的科学有关系； 不精确的几何， 它们是一种意外或者可以理解为对精确几何形状的近似估计； 非精确但严密的几何， 它们与模糊和游牧的思想有关联。 另外， 上面的引文中一开始就提到“王权科学”和“游牧科学”， 它们分别对应于德勒兹的两种空间， 即“条纹空间”和“平滑空间”， 与条纹空间对应的是精确的几何， 而与平滑空间对应的是”非精确但严密“的几何。

自从阿基米德开始， 科学研究一直拘泥于柏拉图的理念论， 只有理念世界才是真实的世界， 现实世界的物体是对理念世界的模仿， 所有科学研究一直隐藏着胡塞尔所说的给现实世界披上一件“理念的衣裳”这样的动机。 理念的衣裳使得科学的世界成为线性的、 同质化的世界， 所有物体问题的表征空间都是在笛卡儿坐标系统的虚构空间中展开的， 在虚构的坐标系统中点与点、 点与线之间的关系是静态的关系， 所以那是一个均质的、 静态的空间， 也是一个无生命的空间， 即德勒兹所言的条纹空间。 条纹空间的技术化模型就是编织物， 编织物由垂直和水平的两种并行的要素构成， 二者垂直地交织在一起。 德勒兹用象棋来说明条纹空间。 象棋的棋子是被编码的， 它们具有内在性和各种内在属性， 由此而衍生出它们的运动、 处境和对峙。 它们是有个性的， 马就是马， 卒就是卒， 象就是象。 每一个都是被赋予了相对权力的陈述的主体。[5]274所以， 象棋所代表的条纹空间具有严格的等级制度， 同时具有不可变的内在属性， 而这些固化的性质使得其中的元素必须按照自己的先天角色行使自己的权力， 采取相应的行动和策略。 这种空间是一个封闭的空间， 不能够随机应变、 适应环境和适应时代变迁， 它固守着自己的特定属性， 从不改变。 因此， 条纹空间是被等级化的、 固定的、 静止的、 保守的、 稳定的、 封闭的、 同质的空间， 具有王权的、 帝国的本质。

与条纹空间相对的是平滑空间。 德勒兹平滑空间理论是基于空间生成与运动的研究理论。 平滑空间不具有同质性， 空间中所有的点都是异质的， 除非是在无限邻近的点之间才具有相似性， 空间中不同域之间的连接没有任何确定的路径。 它是触觉的空间而不是视觉的空间， 它是“一个场， 一个异质的平滑空间与一种极为特殊的多元体的类型联结在一起：非度量的、 无中心的、 根茎式的多元体， 它们占据着空间， 但却不‘计算’空间， 因而， 只有通过‘实地采样才能探索它们’”[5]532。 与条纹空间的象棋比喻不同， 平滑空间则用围棋比喻。 象棋的每一个棋子都被赋予了一种相对的权力； 而围棋的棋子则正相反， 它们是基本的算数单位， 不具有任何身份， 只有一种匿名、 集体性的功能。 围棋的棋子不具有内在属性， 只具有情境性的属性(这也是2016年阿尔法狗战胜李世石震惊全球的原因)。 因此， 这两种棋组成的空间也完全不同， 象棋是在一片封闭的空间内进行部署， 而围棋是在一个开放的空间进行列阵。 象棋对空间进行编码和解码， 而围棋对空间进行结域与解域。[5]505-506因此， 平滑空间中的运动具有游牧的性质， 它是一个开放的、 无中心的能量场， 其中蕴含了各种异质元素以游牧的方式作用于空间， 形成了赋予表达性的空间变化节奏， 这一节奏又构成了平滑空间中的一个个界域。 平滑空间强调向量、 方向、 流动， 这就类似于游牧民在沙漠中寻找水源和植被的空间轨迹。 由游牧科学所建构的空间也具有动态、 开放、 不受任何条件束缚的特征， 它可以作用于空间中的所有的点， 而不是被空间掌控于从一点到另一点的运动之中。 因此， 游牧空间中的运动是点与点之间的自由活动， 就如同游牧民在草原上生活的轨迹是开放、 自由、 不确定的， 即变量永远处于变化的状态之中。 平滑空间中的几何学不同于条纹空间中的几何学， 此时的几何学呈现为“非精确但严密”的特征。 这种几何学与时空中的可能形态、 图形， 还有运动状态、 形状变化等打交道， 如或多或少光滑的面， 或多或少粗糙的棱。 正是平滑空间的灵活的、 运动的、 开放的、 异质的、 非度量的本质， 所以它具有“非精确但严密”的几何学性质。

那么， 除了能对这种“非精确但严密”的几何做特征上的经验描述， 还能否给出一个数学形式上的描述呢？德勒兹认为黎曼几何符合他的平滑空间的论述， 由此他引用了黎曼(Lautman)的描述：

黎曼空间缺乏任何一种同质性。 每一个黎曼空间的特征都体现为表达的形式， 后者界定了两个无限接近的点之间间距的平方……由此得出， 在同一个黎曼空间之中的两个相邻的观察者可以对紧邻它们的点进行定位， 但却无法通过它们之间的关系来对它们自身进行定位， 除非借助新的约定。 每一个邻域因而就是作为一个微小的欧式空间的片段， 但一个邻域和下一个邻域之间的关联是未被限定的， 因而可以通过无限种不同的方式来形成此种关联。 这样， 最一般的黎曼空间就自身呈现为一个由并置但却并未依附在一起的片段所构成的无定形的集合。[5]700

我们知道， 对于平面几何学而言， 它处理的是像点、 直线、 三角形、 圆等规则的几何体， 这些几何体的变化是规则的、 可预先决定的， 这些几何体之间的关系也是固定的， 如三角形的三条中线相交于一点， 经过圆的直径的圆周三角形为直角三角形等， 这样的几何变换空间相当于德勒兹所说的条纹空间。 而对于曲线， 其走势灵活多变， 采用传统的平面几何方法根本无法把握曲线的灵活多变的形状， 相当于德勒兹的平滑空间。 曲线形状的研究是笛卡儿引入笛卡儿坐标系之后(即x,y轴)才开始的， 因为任何一条曲线， 只要把它放入坐标系之中， 这条直线上的每一个点就会对应一组(x,y)值， 我们就可以建立起相应的数学方程， 如直线方程、 圆的方程、 抛物线方程、 双曲线方程等， 这样， 传统几何学中形状的关系完全可以用代数的方法来加以处理。 坐标几何大大扩展了几何学的研究范围， 但是， 坐标几何是在坐标框架之中处理几何图形问题的， 其图形完全在坐标框架范围之内加以限定， 这样建立的曲线方程实际上还是条纹空间中的一种编码， 如抛物线方程y=2x2+3x+4， 实际上是把其中每一个点用两个数值编码之后确定的。 因此， 笛卡儿坐标系对曲线的研究是由一维的观察走向二维的观察， 或者说一维的线性对象必须嵌入二维的面中加以研究。 与此类同， 二维的曲面必须嵌入三维空间才能加以研究， 它们都还是在条纹空间中处理问题。

只有当牛顿和莱布尼茨发明微积分之后， 基于解析几何和微积分发展起来的微分几何才使得处理任意曲线和曲面的问题较为完满地得到解决。 但是， 在古典微分几何中， 人们常常将曲线和曲面放在三维笛卡儿坐标的欧氏空间中来处理相应问题。 曲线和曲面的很多几何特性的描述与讨论， 常常依赖于它们以什么方式嵌入高层空间。 但事实上， 很多几何物体的重要性质本质上是内蕴的， 与它们嵌入高层空间的方式无关。 早年的几何学家很少注意这一点。 高斯与黎曼开始真正意识到这个问题。 “高斯提出了一个完全新的概念， 即一张曲面本身就是一个空间。 这个概念后来为黎曼所推广， 从而在非欧几里得几何学中开辟了新的远景。”[6]301黎曼在其著名的几何学演讲中， 正式地用内蕴的观点重新讨论了几何学的诸多概念。 “黎曼提出的空间的几何并不是高斯的微分几何的推广， 他重新考虑了研究空间的整个途径。”[6]310许多几何概念都可以用内蕴的方式直接定义而摆脱外部空间和坐标系选择的干扰， 比如切向量、 余切向量、 联络、 外微分、 曲率、 挠率、 度量等基本的概念。 这种几何学也就是通常所说的“内蕴几何学”， 如此， 曲线和曲面都不需要嵌入高维空间加以处理， 在局部就可以处理好它们的游走趋势， 由此也基本符合德勒兹追求游牧科学的理念。

当然， 内蕴几何学是否真的能够代表德勒兹的平滑空间恐怕德勒兹本人也未做严格的审查， 因为内蕴几何学毕竟建立在笛卡儿坐标系的基础之上。 所以德勒兹在讨论完黎曼空间后采用一种辩证的眼光看待黎曼空间的平滑性：“不过， 二者是相互关联， 彼此推进的。 没有什么是完结了的：平滑空间令其自身被纹理化， 同样， 纹理化空间也重新给出一种平滑空间……也许必须说， 所有的发展进程都是通过纹理化空间并在纹理化空间中形成的， 但所有的生成却都是在平滑空间中实现的。”[5]701这里面还涉及一个重要的概念“生成”， 此处不多作解释， 就这里论及的内蕴几何学而言指曲面的游走成长的趋势， 即从一种动态的观点看待曲面。

另外， 平滑空间是不可度量的， “它自身是非度量性的， 去中心的， 方向性的等等”[5]698。 就此而言， 平滑空间的几何学具有拓扑特性。 拓扑学就是研究拓扑空间在连续变换下保持不变的性质。 在拓扑学里不讨论两个图形全等的概念， 但是讨论拓扑等价的概念。 比如， 圆和方形、 三角形的形状、 大小不同， 但在拓扑变换下， 它们都是等价图形； 足球和橄榄球， 也是等价的。 也就是说， 从拓扑学的角度看， 它们的拓扑结构是完全一样的。 拓扑学虽然没有度量上的精确， 但不失结构上的严密。

三、 “非精确但严密”的科学与设计

“非精确但严密”这个说法看上去很是深奥， 甚至有些拗口， 但对于科学中新的空间组织和新的材料组织而言却是十分关键的。 致力于生命物质研究的学科如胚胎学、 病毒学、 生物学和地质学最近开始率先发展模糊形式的令人信服的几何学描述。 每当我们需要研究难以测量的对象时， 我们就需要“非精确但严密”这样的思想风格或研究风格。 特别是生物科学的研究， 德兰达在《强度科学与潜在哲学》中举过很多相关例子， 如爱德曼(Edelman)处理他的细胞集合体的方式， 这些集合体的成分的精确数量或它们的确切位置是无法确定的。[7]52这种对待定量精度的态度并不表明， 生物学家是粗心或者是不严格的。 相反， 它表明一种更复杂精致的拓扑学思想风格， 而且这种基于拓扑风格的精度在自然界中处处存在。 对此， 德兰达引用生物学家亚瑟·温弗里(Arthur Winfree)的话加以佐证：“生命科学从未羡慕数量上的精度……但这并不意味着生物科学本质上是草率的、 模糊的、 不准确的和不科学的。 一条大马哈鱼是如何找到回家的路， 并在俄勒冈州它三年前离开的同样的小河里产卵？一条一米长的、 有着数十亿核苷酸碱基对的序列如何通过可逆盘绕进入直径不超过几千碱基对的细胞核而没有纠缠在一起？……这样的奇迹预示着可再现的精度。 但精度不是那种我们所知道的如何写方程， 也不是那种我们可以测量到小数点后八位数的那种。 这是一个更加灵活的精确性， 它回避量化， 就像一个细胞膜将其划分为内外两个部分， 在这错综复杂的区域甚至没有一个病毒大小的洞的精确性一样：拓扑的精密， 不在乎外形、 力和时间的定量细节。”[7]53-54

除生物科学之外， 材料科学也需要大量运用“非精确但严密”的思考方式， 因为材料科学属于质料性科学。 自古以来， 在哲学上“质料”都是与“形式”相对而言的， 所以形成了“质料+形式”的思维模式， 而且近现代科学更为重视形式方面的研究。 物理学家把物质变为一般性的“质量”， 即物质所含物质的量的多少， 作为一个广延量； 化学家发现了原子及原子的结构而忽视了物质本身所固有的属性。 他们都关注于各向同性的东西， 反而把物体本身所固有的差异给忽视了。 大多数哲学家也不大关心质料， 或者关心质料的也把质料从属于形式加以研究， 或者从质料上升为形式加以升华， 从而在普遍性上加以论述。 然而， 对于丰富的物质世界， 这种“质料+形式”的简单化的思维方式遭到德勒兹的批判， 他说：“作为游牧科学的要素， dispars则指向质料-力， 而非质料-形式。 在这里， 准确地说来， 问题不在于从变量中抽取常量， 而在于将变量自身置于连续流变的状态之中。”[5]531简单地说， 采用“质料+形式”的方式研究物质材料， 此时的几何学是观念化的精确的几何学， 精确的几何学只能研究物质的外部边界， 但不能研究物质的内在生成。

早期的工匠通过实际接触、 操作那些材料来了解物质本身的性能， 那些人在切、 削或塑性变形等热处理过程中亲身感受到材料性能的复杂性。 但是随着化学的发展， 这些早期想要掌握物理蜕变和物理结构对于材料属性影响的复杂性的企图， 都败给了化学的简化处理：单独成分的行为或者是服从定比法则的物质的行为。 这种简单化符合学科专项研究的要求， 由其产生的制造方式也适合大规模生产的需要。 但是， 它也带来了很多问题。 首先， 19世纪把技术从工匠转移到机器的过程， 是和金属性能的均质化相辅相成的。 但是因为材料复杂性能的大部分知识是由科学界之外(比如工匠)的经验发展的， 那么， 伴随着机械化， 降低技术难度必然导致部分工匠技术知识的损失。 其次， 简单化和条例化不只出现在制造过程中， 它也影响了设计过程， 它甚至使得许多结构工程师不知道如何用各向异性的材料来进行设计， 而正是各向异性的设计能力能够处理用新的复合材料设计结构所需要的复杂的、 连续变化的行为。 再就是人们对简单化和统一性的需求超越了制造和设计。 过去几个世纪中， 很多其他事物也变得均质， 比如农场里牲口和农作物的遗传物质因为转基因作物的发展和传播变得更加同质； 再比如随着义务教育系统和大众传媒的影响， 我们的语言材料也变得更加同质， 异质的方言开始向标准语屈服； 等等。 因此， 对同质的追求严重危害了物质哲学。 对此， 德勒兹花了很大的篇幅描述了早期冶金技术的游牧特性。 对于金属锭块的加工， 德勒兹说：“更应该构想的不是相互分离的节段， 而是一根流动作坊构成的链条， 从一个洞到另一个洞， 这些作坊形成了一条流变之线， 一条坑道。”[5]599“工匠就是巡游者、 流动者。 跟随着物质流， 就是巡游， 就是流动。 这是处于活动中的直觉。”[5]591德勒兹《千高原》中的《1227年——论游牧学：战争机器》一文对物质科学的论述简直可以算作一种新物质主义的宣言， 也可以看作一篇工匠哲学的力作。

西里尔·斯坦利·史密斯(Cyril Stanley Smith)作为一个冶金学家同时也是一位材料历史的专家， 探索了西方物质哲学从古到今的发展历史， 得出结论：在大多数时候， 材料行为复杂性和可变性的研究一直是实证为本的工匠和工程师(而不是哲学家或是科学家)的关注点。 史密斯的结论表达了他对于当前物质哲学研究问题的看法。 正因为史密斯有如此洞见， 他开始采用一种新的方式研究无机物的性质。 他从将简单的拓扑学应用于金属晶粒的形状开始， 拓展到多层次结构的各个层次。 他的一项非常著名的工作(成果发表于1952年)是将金属多晶与一个减小空气压力条件下的肥皂泡相比较， 显示了晶粒生长动力学与泡沫生长动力学之间存有一定的相似性。 由此他提出晶界可以理解为具有界面能的表面， 类似于肥皂膜具有一定的表面张力， 并分析了相互接触的多面体在角数、 棱数、 平面数之间的拓扑学关系， 以及不同棱数多面体平面出现的频率分布。 这些现象均可以在金属晶粒、 生物细胞组织和肥皂泡中观察到。[8]

除生物学、 材料学之外， “非精确但严密”的几何学现在被美国当代建筑设计大师林恩运用于建筑设计之中。 林恩从拓扑学、 哲学、 生物学、 地质学等学科的角度来研究建筑， 特别是以德勒兹的哲学为基础， 探索一种基于生长与突变概念的设计模式。 采用德勒兹的平滑空间理论， 林恩寻求重新配置建筑学中物体和几何间的关系， 从而突破传统建筑物对僵硬的条纹空间的依赖， 创造出折叠建筑的设计模式。 对林恩来说， 折叠建筑并不是传统建筑固定的空间样式， 其本身是建立在“有机体和几何语言之间的协定”[9]41之上。 物体变成褶皱折叠式的多样性， 而几何学变成德勒兹所说的一种“非精确但严密”的几何学形式。 例如球形设计他突破几何学中固有的“球”的概念， 采用一种“滴状物”的动感形状， 他说：“关于这些拓扑几何学的组织的阐释实际上表明了一种新的复杂性拓扑学的工作模式。 在滴状物模型中， 物体被定义为一群靠内力吸引在一起的单体， 与通常情况下的几何原型(如球体)所不同的是， 它有自己的组织， 一个可塑的球体被定义在与其他物体的关系之中， 它的中心、 表面积、 体量的组织被其他方面的影响所决定。”[9]174林恩的工作因此建立起了一种理论并使得“精确的、 多样的、 暂时的物体”和“更灵活的变形几何”之间发生了内在的联系。 限于篇幅， 此处不多做介绍。

四、 结语

“非精确但严密”的科学的应用面是非常广阔的， 本文只选取了几何学这一维度， 而且几何学中分形几何学维度方面的内容限于篇幅未做阐释， 实际上还可以涉及工艺、 语言、 写作、 中医、 政治、 法律、 战争、 人工智能等方面的内容。 其思维的核心点在于从那种外在的、 固定的框架思维模式中走出来， 从而走入一种内在的、 游动的、 无定向的过程中去。 从外在的框架所得到的结论无非就是人为的精确， 但内在的游走却可以趋近于物质世界的丰富细密的结构。 现代数学也努力使得这一思想形式化， 如“非精确几何学”“拓扑动力学”“分形几何”等都源于这一思维走向。 “非精确但严密”科学的思想虽起源于胡塞尔， 但胡塞尔最多只是从几何考古学的角度论及它， 是德勒兹、 德兰达等哲学家丰富了它的研究内容。

[1] 林德伯格.西方科学的起源[M].张卜天，译.长沙：湖南科学技术出版社，2003：89-90.

[2] 胡塞尔.纯粹现象学通论[M].李幼蒸，译.北京：商务印书馆，1995.

[3] 胡塞尔.欧洲科学的危机和超验现象学[M].张庆熊，译.上海：上海译文出版社，2005.

[4] 德里达：胡塞尔《几何学的起源》引论[M].方向红，译.南京：南京大学出版社，2004：134.

[5] 德勒兹,加塔利.资本主义与精神分裂:卷2 千高原[M].姜宇辉，译.上海：上海书店出版社，2012.

[6] 克莱因.古今数学思想:第2卷[M].北京大学数学系数学史翻译组，译.上海：上海科学技术出版社，1979.

[7] DE LANDA M.Intensive Science and Virtual Philosophy[M].New York:Continuum,2005.

[8] 康 R W.走进材料科学[M].杨柯，译.北京：化学工业出版社，2008:69.

[9] LYNN G.Folds,Bodies and Blobs[M].Brussels:La Lettre Volee,1998.

[责任编辑 尚东涛]

The “Inexact yet Rigorous” Science— Taking Geometry as a Clue

TAO Jian-wen

(ResearchCenterforPhilosophyofScienceandTechnology,SouthChinaUniversityofTechnology,Guangzhou510640,China)

A vague type of pro-geometry thought was put forward by Husserl in his later philosophy study, which was developed by Deleuze as an “inexact yet rigorous” science. Its quintessence is to get into a kind of internal, nomadic and non-directional differential process instead of being trapped by the external, fixed, precise and homogeneous artificial framework. This kind of science has both ambiguity of its boundary and precision of its inner structure, widely applied to many fields of research like biology, material science, space design and so on.

inexact yet rigorous; smooth space; material

2016-05-07

陶建文(1968—)， 男， 湖南华容人， 博士， 华南理工大学马克思主义学院教授， 主要研究方向为科技哲学。

N031

A

1009-4970(2017)01-0010-07