配送中心选址的自适应Levy分布混合变异鱼群算法
2017-03-01张立毅孙云山
费 腾 张立毅 孙云山
(天津商业大学信息工程学院 天津 300134) (天津大学电子信息工程学院 天津 300072)
配送中心选址的自适应Levy分布混合变异鱼群算法
费 腾 张立毅*孙云山
(天津商业大学信息工程学院 天津 300134) (天津大学电子信息工程学院 天津 300072)
在建立配送中心选址模型的基础上,提出一种解决配送中心选址的自适应Levy分布混合变异人工鱼群算法。该算法将公告板的历史最优鱼个体代替当前鱼群中最差鱼个体,形成中间鱼群。在中间鱼群中,对历史最优鱼个体进行混沌变异,其他鱼个体进行Levy变异。Levy变异的引入,对于算法跳出局部最优解起到更好的引导作用,保持了鱼群的多样性。混沌变异的引入,增强了算法局部搜索的能力,保证了算法后期的收敛速度。通过算例仿真表明,Levy分布混合变异人工鱼群算法比基本鱼群算法更能有效解决配送中心选址问题,寻找到更低的费用成本。
人工鱼群算法 Levy分布 混沌 变异 配送中心选址
0 引 言
配送中心的选址作为物流系统的极其重要组成部分,居于重要的枢纽地位,其规划的好坏直接关系到整个物流系统规划的成败[1-2]。在物流系统分析与设计时,物流配送中心选址常需要得到模型化、数量化的支持[3]。物流配送中心选址模型主要分为单一配送中心选址模型及多配送中心选址模型两种。单一配送中心模型求解方法主要包括重心法,交叉中值法,因素分析法及层次分析法等。多配送中心选址模型的求解方法主要包括混合0-1规划法、CFLP法、P中值法等。近些年由于智能算法的飞速发展,且配送中心选址问题属于离散的组合优化问题, 具有NP性质,学者们开始将智能算法运用到物流配送中心选址中。2008年,刘倩[4]用模拟退火算法的迭代得到了配送中心选址模型的最优解,通过实例验证了模拟退火算法对于物流系统的优化具有一定的实用价值。2010年,郝栋梁等[5]在建立配送中心选址数学模型的基础上,利用遗传算法求解配送中心选址问题,并通过具体算例进行验证。同年,许婷等[6]将 GIS 和蚁群算法结合,在解决最短路径问题上得到了较好的效果,并基于该最短路径构建了选址运输费用模型,使选址运输费用分析更接近实际运输环境。2013年,瞿斌等[7]依照更具有现实意义的“加工厂—配送中心—用户”的模式建立物流配送中心连续型选址模型,并针对较大规模的选址问题提出改进粒子群求解算法。近些年来,不断有学者对于配送中心选址问题的解决提出大量的改进算法,但基本都局限于上述提及的粒子群算法、退火算法、遗传算法及蚁群算法的改进上,而极少有鱼群算法及其改进算法应用于配送中心选址问题上。
本文是在建立配送中心选址模型的基础上,提出了一种解决配送中心选址的自适应Levy分布混合变异人工鱼群算法。该算法将公告板记录的历史最优鱼个体代替当前鱼群中最差鱼个体,形成中间鱼群。在中间鱼群中,对历史最优鱼个体进行混沌变异,其他鱼个体进行Levy变异。由于Levy分布具有厚尾特性,使得Levy变异扰动作用更将强烈,对于算法跳出局部最优解起到更好的引导作用,保持了鱼群的多样性。混沌变异的引入,增强了算法局部搜索的能力,保证了算法后期的收敛速度。通过算例仿真表明,Levy分布混合变异人工鱼群算法比基本鱼群算法更能有效解决配送中心选址问题,寻找到更低的费用成本。
1 配送中心选址问题
配送中心选址模型所要解决的问题是已知有n个需求点的前提下,要在其中设定m个配送中心,使得选定的配送中心与其配送范围内的需求点之间的运输费用最小。
为了方便配送中心选址模型的建立,假设如下:
(1) 配送中心的供应量总可以满足需求点的需求,并由其配送范围内的需求量决定;
(2) 一个需求点有且仅有一个配送中心配送;
(3) 只考虑一级运输情况,即只考虑从配送中心到需求点的费用,不考虑从工厂到配送中心的费用。
故建立如下模型[8]:
(1)
式(1)为目标函数,其目标为从选择的配送中心到其配送范围的需求点的运输费用最小。其中,Z表示运输费用,m表示配送中心的个数,n表示需求点的个数,Dk表示需求点的需求量,djk表示配送中心j到需求点k的距离。yjk是0-1变量,当yjk取值为1时,表示需求点k由配送中心j配送。
(2)
式(2)确保每个需求点仅有一个配送中心配送。J表示配送中心集合,{j|j=1,2,…,m},K表示需求点集合,{k|k=1,2,…,n}。
(3)
式(3)表示选择配送的个数为P。zj为0-1变量,当zj取值为1时,选择j为配送中心。P表示选择配送中心的个数:
yjk≤zjj∈Jk∈K
(4)
式(4)确保每个需求点必然有与之对应的配送中心。
yjk∈{0,1}j∈Jk∈K
(5)
zj∈{0,1}j∈J
(6)
式(5)、式(6)为yjk及zj的定义式。
2 自适应Levy分布混合变异鱼群算法
2.1 人工鱼群算法AFSA
基本鱼群算法数学模型如下:
用X=(x1,x2,…,xn)来描述各个人工鱼的位置,用Y=f(x)来描述当前人工鱼所在位置的食物浓度,其中xi为寻优变量,Y为寻优的目标。δ表示拥挤度因子;step表示人工鱼移动的步长;Trynumber表示人工鱼每次觅食最大的试探次数。
人工鱼的当前位置为xi,在视野允许范围内随机选择下一个位置xj,假设在处理极小值问题中Yi>Yj,则向xj方向前进一步,否则重新随机选择xj,再次判断是否满足前进条件[9]。若反复次数达到尝试次数Try_number时,随机游动一步。
(7)
式中,rand()为(0,1)的随机数。
(2) 聚群行为
人工鱼当前位置为xi,其食物浓度为Yi,在其视野允许的范围内的伙伴数量为nf,若Yc/nf>δYi,表示伙伴中心位置Xc的食物浓度较高,且周围处在不拥挤状态,则人工鱼向中心位置Xc前进一步,否则执行觅食行为[10]。
(8)
(3) 追尾行为
人工鱼的当前位置为xi,其食物浓度为Yi,在其视野允许范围内能够寻找到的食物浓度最高时的人工鱼位置为xmax,若Ymax/nf>δYi,表示处于xmax位置的人工鱼具有较高的食物浓度,且周围不拥挤,可以向xmax位置前进一步,否则执行觅食行为。
(9)
2.2 自适应Levy分布混合变异鱼群算法ALMM-AFSA
自适应Levy分布混合变异人工鱼群算法主要用于克服在基本鱼群算法后期,大部分人工鱼个体容易聚集在局部最优附近而非在全局最优附近聚集,或者人工鱼个体漫无目的的随意游走,使得整个基本鱼群算法全局搜索受限,陷入局部最优,严重影响到算法的搜索精度、收敛速度及稳定性等方面[11]。自适应Levy分布混合变异人工鱼群算法改进的核心思想是当基本人工鱼群算法在非全局最优严重聚集时,用公告板上的记录的历史最优鱼个体替代当前状态下的最差鱼个体,形成中间鱼群。对中间鱼群中的历史最优鱼个体采取混沌变异,其他鱼个体采取Levy变异。采取混沌变异的作用是使得改进算法在跳出局部最优的束缚的同时增强局部搜索的能力。对其他鱼个体采取Levy变异的作用是增加人工鱼的多样性,提高全局搜索的能力,引导人工鱼向历史最优鱼的方向移动,从而使基本鱼群算法在搜索精度、收敛速度及稳定性等方面的能力得到增强。
(1)Levy分布
按比例分配是在实际生活中经常碰到的问题,它的数学意义就是应用比把一个数量按照一定的比例来进行分配,在教学中可以结合实际创设合适的情境,通过一些生产、生活中的实例来呈现教学内容,既能吸引学生,激发学生的学习兴趣,又能让学生体验按比例分配的数学意义,体会数学来源于生活而又服务于生活的辩证思想。
在19世纪30年代Levy[12]提出Levy分布,式(10)为其概率密度函数。
(10)
其中,α,γ为Levy分布的两个特征参数。0<α≤2,γ>0。α用来控制分布图形的锐度,γ用来控制分布的尺度单位。当α=2时,Levy分布等同于高斯分布,当α=1时,Levy分布等同于柯西分布[13]。对于一般的α取值,通过Levy分布的概率密度函数分析起来比较困难,所以利用数值模拟算法来产生Levy分布随机数[14]。
假设产生两个独立同分布的随机变量x、y,其标准差分别为σx、σy。σx和σy取决于参数α,且相互影响。因此,令σy=1,则σx只受参数α的影响。如下产生变量v:
(11)
变量w通过如下非线性变换用以服从Levy分布:
(12)
为了获得尺度单位因子γ不为1的Levy分布,做如下线性变换:
(13)
其中,σx、K(α)以及C(α)的值可以通过文献[15]查表得到。根据上述步骤得到的分布能够快速准确地收敛于Levy分布。
(2) 传统变异
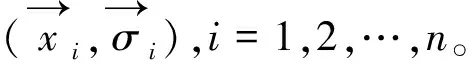
(14)
(15)
(16)
(17)
其中,j=1,2,…,m,N(0,1)用于产生个体的高斯分布随机数,Nj(0,1)用于产生每个分量的新的高斯分布随机数。文献[16]给出了参数τ和τ′的定义,即:
(18)
(19)
(3)Levy变异
在传统变异中,式(16)中δj(t)选取不同分布的随机数时,会产生不同的变异算子。
当δj(t)为Levy分布随机数时,式(16)演变为Levy变异算子,即:
(20)
其中,Lj(t)为服从Levy分布的随机数。
(4) 混沌变异
与Levy分布类似,当δj(t)为混沌随机序列产生的随机数时,式(16)演变为混沌变异算子,即:
(21)
其中,Hj(t)为在[-2,2]区间按照混沌规律变化的序列产生的随机数[17]。混沌序列一般采用一维Logistic映射:
Zk+1=μZk[1-Zk]Zk∈[0,1]
(22)
式中,μ为控制参数,取值为[3.56,4];当μ=4、0≤Zk(0)≤1时,Logistics映射完全处于混沌状态[18],历遍性最强。Hj(t)为通过Zk放大平移后得到。
3 求解流程
步骤1 进行鱼群初始化。设置人工鱼群的规模、初始位置设置、视野、步长、拥挤度、试探次数、最大迭代次数、Levy变异的特征参数及混沌变异的控制参数等,产生初始鱼群。读取需求点的坐标,计算各个需求点之间的距离。设置选择的配送中心的个数。
步骤2 进行公告板初始化。计算各个初始人工鱼个体当前的状态值,利用公告板将最优的费用值记录下来,进行公告板初始化。
步骤3 进行鱼群行为选择。各个人工鱼分别进行追尾行为和聚群行为,评价两种行为后的值,选择值较小的行为作为实际执行的行为,缺省行为是觅食行为[19]。
步骤4 进行公告板更新。一次迭代以后,若鱼群中的最优鱼的费用值大于公告板所记录的费用值,进行公告板的更新替代。
步骤5 判断是否变异。如果公告板上记录的最优费用值在连续多次迭代执行后仍没有改变,且连续的次数达到未改变次数的最大时,执行步骤6;否则执行步骤7。
步骤6 进行变异操作。人工鱼群体中的最差费用个体被公告板上记录的最优费用个体代替,形成一个父代中间种群。在中间鱼群对历史最优鱼进行混沌变异,其他鱼进行Levy变异。计算最优费用值与公告板比较,若优,表明变异成功,更新公告板,同时设置公告板未改变次数为0,执行步骤7;否则,重新变异,若达到最大变异次数时仍不成功就采用最后一次的变异,执行步骤7。
步骤7 记录最小费用及各个配送点的配送范围。
步骤8 判断是否算法终止。判断是否已达到最大迭代次数,若不满足,执行步骤3,否则执行步骤9。
步骤9 算法终止,输出最小费用值及配送方案。
4 算例仿真
假设有28个需求点,从其中选出6个作为配送中心。每个需求点的坐标及需求量如表1所示。设置人工鱼个数为100,尝试次数为100,人工鱼的视野为100,拥挤度因子为0.618,人工鱼移动的最大步长为9,Levy分布的特征参数α为0.8,尺度因子γ为2,混沌变异的控制参数为4,最大迭代次数为30。
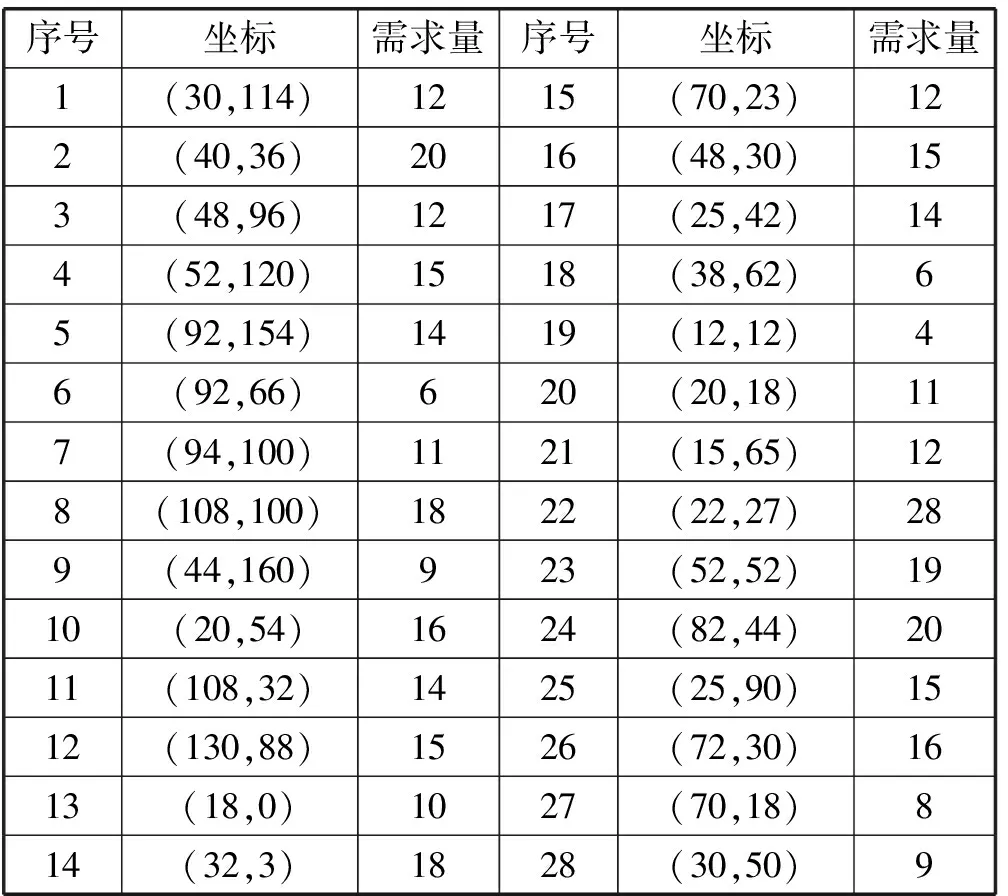
表1 需求点坐标及需求量
表2为利用AFSA解决配送中心选址问题的10次运行结果,表3为利用ALMM-AFSA解决配送中心选址问题的10次运行结果。表4为AFSA选择配送中心及配送的具体方案。表5为ALMM-AFSA选择配送中心及配送的具体方案。表6为AFSA与ALMM-AFSA在配送中心选址分配问题上的性能对比表。
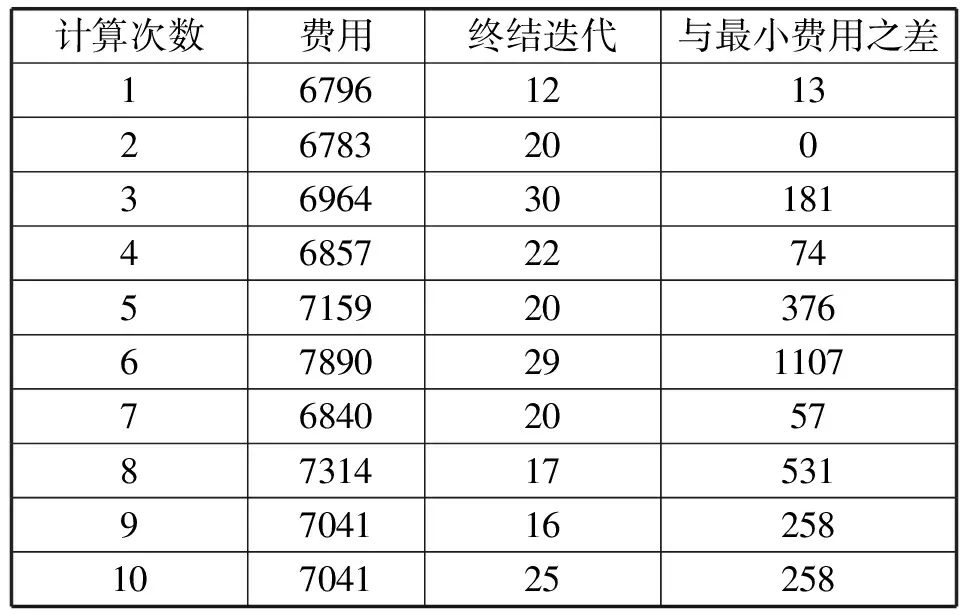
表2 采用AFSA所得实验结果
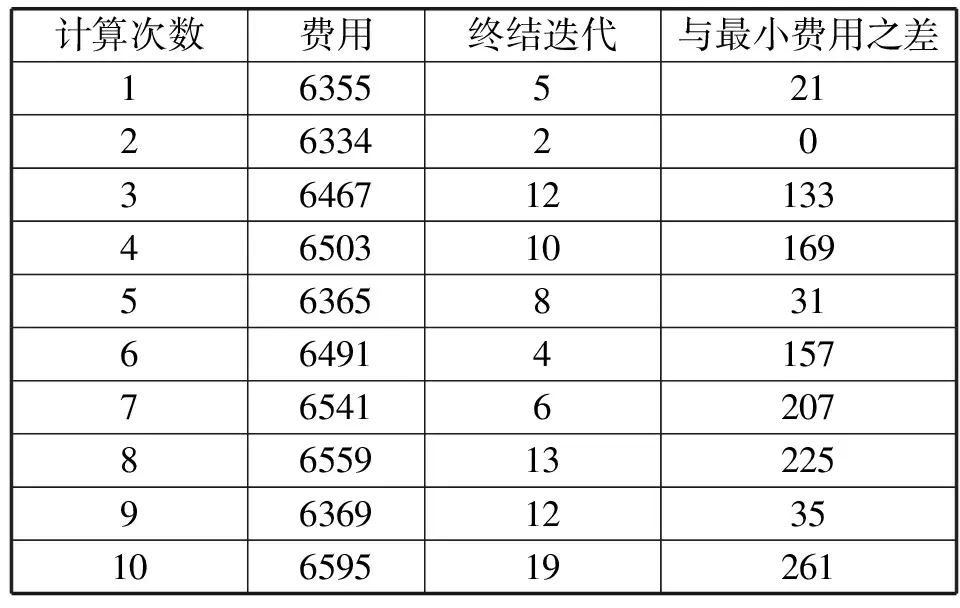
表3 采用ALMM-AFSA所得实验结果

表4 AFSA选址方案
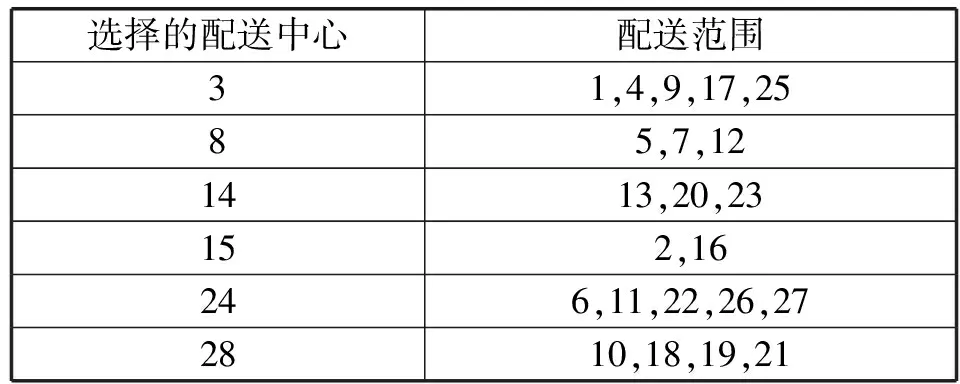
表5 ALMM-AFSA选址方案

表6 性能对比表
图1为AFSA选址方案图,图2为ALMM-AFSA寻址方案图,图3为AFSA与ALMM-AFSA寻优曲线对比图。
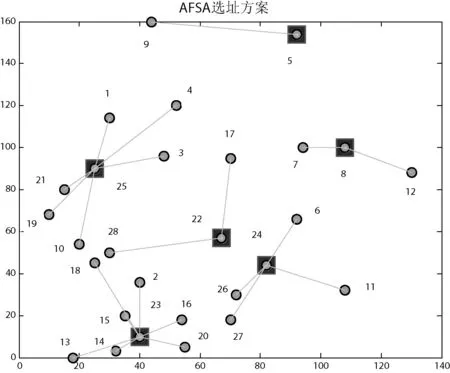
图1 AFSA寻址方案
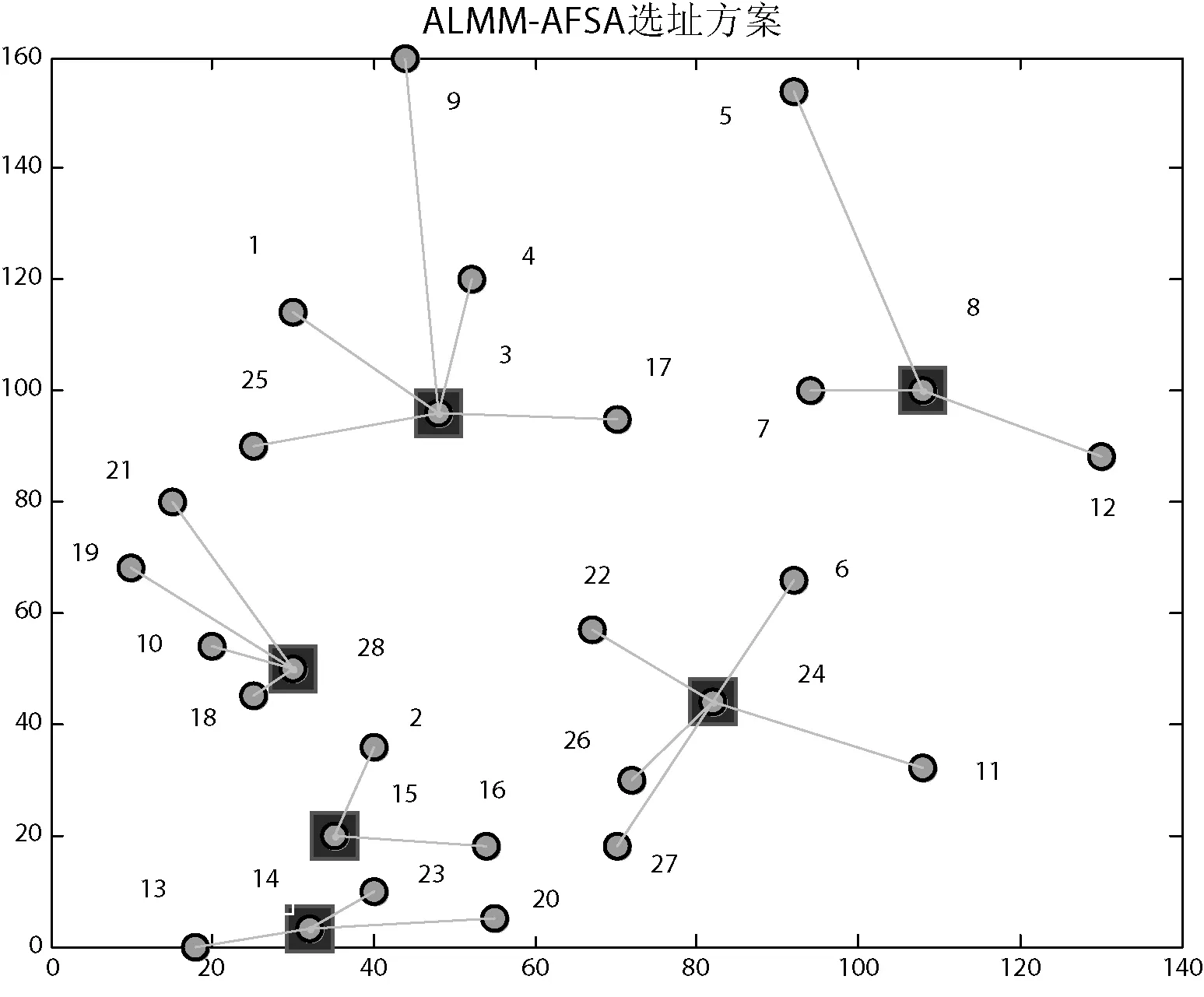
图2 ALMM-AFSA寻址方案
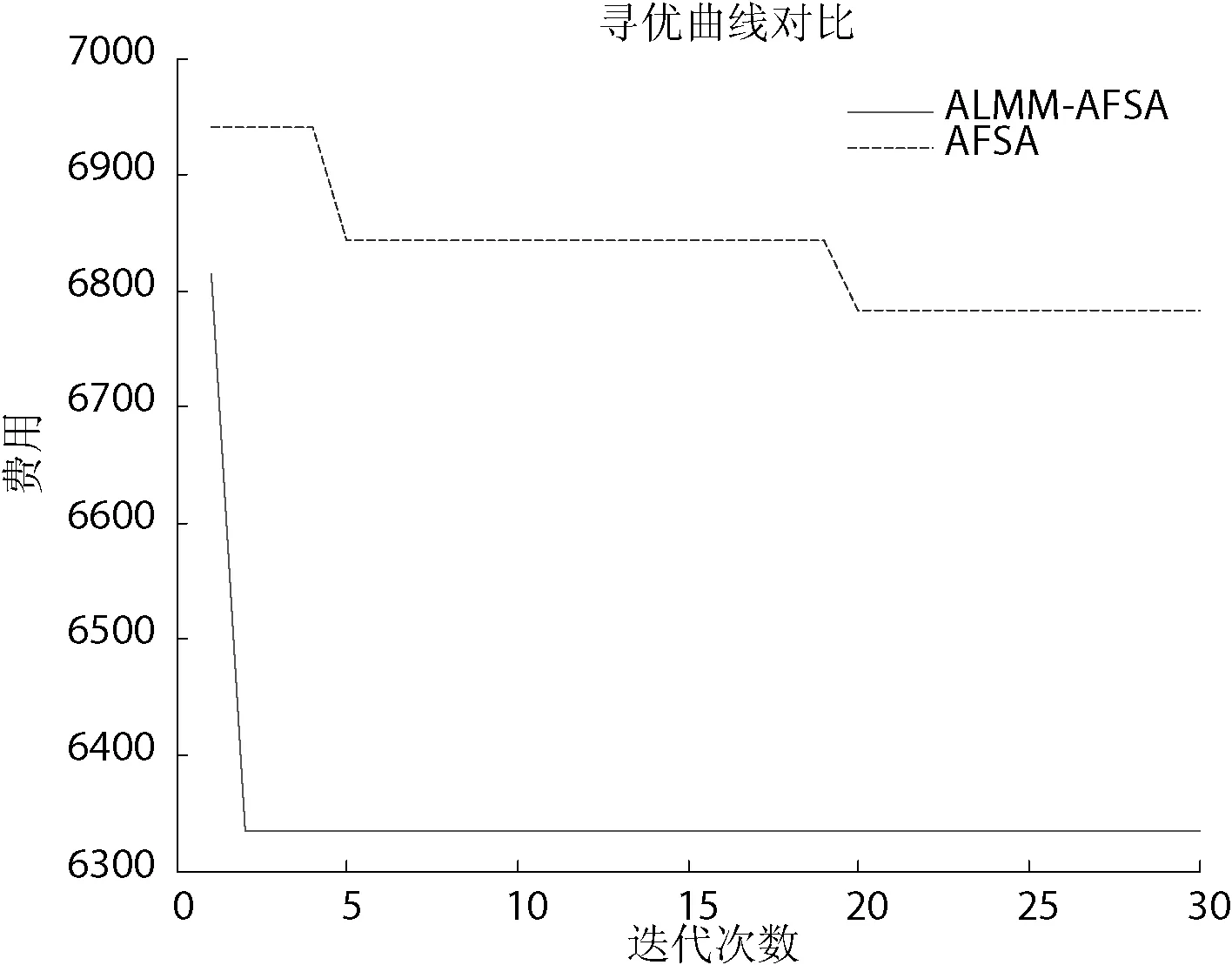
图3 寻优曲线对比图
算例仿真表明,在费用方面,AFSA的最小费用为6783,ALMM-AFSA的最小费用为6334,最小费用节省了6.65%。AFSA的平均费用为7068.5,ALMM-AFSA的平均费用为6458,平均费用节省8.64%。由此可以看出,ALMM-AFSA在求解配送中心选址问题中能够寻找到更低的费用,提高费用利用率。在终结代数方面,AFSA的平均终结代数为21.2,ALMM-AFSA的平均收敛代数为9.1。由此可见,ALMM-AFSA具有更好的收敛速度。在标准差及差的平均值方面,AFSA的标准差及差的平均值为334.74和285.5,ALMM-AFSA的标准差及差的平均值为95.28和123.9。由此可见,ALMM-AFSA在解决配送中心选址问题上稳定性更好。
5 结 语
本文提出了一种新的解决配送中心选址的算法——自适应Levy分布混合变异人工鱼群算法。该算法在基本鱼群算法陷入局部最优时引入Levy变异和混沌变异,通过变异来增加鱼群跳出局部最优的能力,增加鱼群的多样性,从而达到全局寻优的目的。通过实验仿真表明,该算法相比于基本鱼群算法更适合求解配送中心选址问题。但是,由于配送中心模型建立基本处在理想情况下,因此,对于更适合实际环境的配送中心模型的建立是今后进一步研究的方向。除此之外,由于对于鱼群算法的改进研究仍处在初期阶段,因此,对于改进鱼群算法的研究是今后研究的另一个方向。
[1] 李云清.物流系统规划[M].上海:同济大学出版社,2004.
[2] 胡双增,张明.物流系统工程[M].北京:清华大学出版社,2000.
[3] 秦固.基于蚁群优化的多物流配送中心选址算法[J].系统工程理论与实践,2006(4):120-124.
[4] 刘倩.模拟退火算法在配送中心选址的应用[J].交通标准化,2008(8):147-149.
[5] 郝栋梁,汝宜红,徐秀全.遗传算法在配送中心选址的应用[J].物流技术,2010(7):75-77.
[6] 许婷,盛明,娄彩荣.基于GIS和蚁群算法的物流配送中心选址研究[J].测绘科学,2010,35(6):206-208.
[7] 瞿斌,陆柳丝.种群规模自适应粒子群在配送中心连续型选址中的应用[J].运筹与管理,2013,22(3):102-108.
[8] 史峰,王辉,郁磊,等.Matlab智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011.
[9] 吴姗姗,黄友锐.基于改进人工鱼群算法的PID控制器参数优化[J].安徽理工大学学报:自然科学版,2013,33(2):23-26,55.
[10] 潘喆,吴一全.二维Ostu图像分割的人工鱼群算法[J].光学学报,2009,29(8):2115-2121.
[11] 张创业,莫愿斌,何登旭,等.混沌协同人工鱼粒子群混合算法及其应用[J].计算工程与应用,2010,46(32):48-51,54.
[12] Levy P.Théorie de l’Addition des Variables Aléatoires[M].Paris:Gauthier-Villars,1937.
[13] 唐洪,邱天爽,李婷.非高斯alpha稳定分布环境中自适应滤波及研究进展[J].系统工程与电子技术,2005,27(8):1336-1341.
[14] Lee C Y,Yao X.Evolutionary programming using mutations based on the Levy probability distribution[J].IEEE Transactions on Evolutionary Computation,2004,8(1):1-13.
[15] Mantegna R N.Fast,accurate algorithm for numerical simulation of Levy stable stochastic processes[J].Physical Review E,1994,49(5):4677-4683.
[16] Bäck T,Schwefe H P.An overview of evolutionary algorithms for parameter optimization[J].Evolutionary Computation,1993,1(1):1-23.
[17] 骆晨钟,邵惠鹤.采用混沌变异的进化算法[J].控制与决策,2000,15(5):557-560.
[18] 高尚.旅行商问题的混沌蚁群算法[J].系统工程理论与实践,2005(9):100-104,125.
[19] 陈广洲,汪家权,李传军,等.一种改进的人工鱼群算法及其应用[J].系统工程,2009,27(12):105-110.
[20] 王东升.赤峰电网无功优化规划方案研究[D].北京:华北电力大学,2008.
RESEARCH ON MIXED MUTATION ARTIFICIAL FISH SWARM ALGORITHM BASED ON ADAPTIVE LEVY DISTRIBUTION OF THE DISTRIBUTION CENTER LOCATION
Fei Teng Zhang Liyi*Sun Yunshan
(SchoolofInformationEngineering,TianjinUniversityofCommerce,Tianjin300134China) (SchoolofElectronicInformationEngineering,TianjinUniversity,Tianjin300072,China)
Based on the establishment of distribution center location model, the adaptive Levy distribution mixed mutation artificial fish swarm algorithm for solving distribution center location is proposed. In the improved algorithm, the worst individual of the current fish is replaced by the best individual fish of bulletin board toformat theintermediate fish swarm. In the middle swarm, the best individual fish is to carry out the chaotic variation, and the other fish individuals is to carry out Levy variation. The introduction of Levy mutation plays a better role in guiding the algorithm out of local optimal solution, and increases the diversity of fish.Besides,the introduction of chaos mutation enhances the local search ability of the algorithm and guarantees the convergence rate of the algorithm. The simulation results show that the adaptive Levy distribution mixed mutation artificial fish swarm algorithm are more effectively than artificial fish swarm algorithm to solve the distribution center location problem and find the lower cost.
Artificial fish swarm algorithm Levy distribution Chaos Mutation Distribution center location
2015-10-29。国家软科学研究计划项目(2014GXS4D089);天津市高等学校科技发展基金计划项目(20110709);天津市科技特派员项目(15JCTPJC63000);中国物流学会项目(2014CSLKT3-16)。费腾,实验师,主研领域:智能计算。张立毅,教授。孙云山,副教授。
TP391.1
A
10.3969/j.issn.1000-386x.2017.01.046
