基于混合混沌粒子群算法的装配线平衡问题研究

鲁建厦，朱 恺，董巧英

(浙江工业大学 机械工程学院，浙江 杭州 310014)

基于混合混沌粒子群算法的装配线平衡问题研究

鲁建厦，朱 恺，董巧英

(浙江工业大学 机械工程学院，浙江 杭州 310014)

为了实现装配线多目标最优化平衡，建立了以装配线平衡率与平滑指数最优化为目标函数的多目标装配线平衡模型.由于粒子群算法在求解时易发生“早熟”现象，陷入局部最优的缺陷，因此引入模拟退火算法与混沌思想，设计了一种三者相融合的混合混沌粒子群算法.算法借助混沌所具有的遍历性、随机性及规律性，对粒子速度的更新调整进行干预；利用模拟退火算法在一定范围内以变化的概率接受较差解的特点，有效抑制“早熟”现象，实现对于装配线的平衡优化，通过实例验证了算法的有效性.

装配线平衡；融合优化；模拟退火；混沌；粒子群算法

装配线平衡问题(Assembly line balancing problem，简称ALBP)一直都是制造领域中极为重要的一项研究课题，其平衡与否将直接对企业的生产效率、生产成本、市场竞争力产生巨大影响.Bryton于1954年首次系统论述了装配线平衡问题，并提出了一种“会聚过程法”来解决ALBP[1].Scholl等[2]采用分支定界法来高效寻找装配线平衡的最优解，基于“局部下界”理念提高算法求解效率.Mcmullen等[3]采用模拟退火算法来解决带有平行工作站的多目标的装配线平衡问题.彭慧等[4]对混流装配线第二类平衡问题展开研究，建立以加权平均负荷和生产节拍加权和的求解模型，并采用遗传算法进行模型求解.刘炜琪等[5]提出一种改进的多目标粒子群算法来求解所建立的以最小化超载时间、总切换时间以及产品变化率为优化目标的模型.李明等[6]采用变异粒子群算法来求解ALBP，在标准粒子群算法的基础上，对设定步长内位置没有更新的个体采用多点变异的方法来提升种群的多样性，并通过纵向进化与横向搜索的机制，提升算法综合搜索性能.实际生产过程中，多项衡量指标均会对装配线的平衡与否产生影响，单一性的指标衡量无法准确做到真正意义上的最优化平衡.因此，需要考虑多目标衡量的装配线平衡优化，研究以装配线平衡率与平滑指数相融合来衡量装配线的平衡优化程度.

1 装配线平衡模型构建

装配线平衡问题的定义为：装配生产线上，被加工对象依序沿装配线流动，在满足各作业元素装配生产优先顺序的约束前提下，合理优化分配各作业元素至一定数量的线上工作站，确保各工作站的作业时间总和基本相近且不超过生产节拍，尽可能减少工人与机器停顿等待现象的出现，实现生产目标的最优化[7].根据优化目标的区别，装配线平衡问题通常分为三类：1) ALBP-I型：已知装配线的生产节拍，求最小化的工作站总数；2) ALBP-II型：已知装配线的工作站总数，求装配线生产节拍的最小化；3) ALBP-III型：已知装配线的生产节拍和工作站总数，求装配线平滑指数的最小化.

在平衡优化过程中，企业既对装配线的平衡率非常看重，平衡率越高则表明整条装配线的效率更好；又对装配线的平滑指数密切关注，平滑指数越小则表明装配线上各工作站彼此间的工作负荷更为均衡，装配线整体平衡性更佳.因此，采用目标加权平均的方法同时考虑装配线平衡率和平滑指数，以融合优化的思维来解决装配线平衡优化问题.在装配线工作站总数给定的前提下，将装配线平衡率与平滑指数融合为新的最优化目标函数，其数学描述如下所述：

1) 平衡模型建立的条件假设.装配线上只生产单一品种的一类产品；作业元素为最小且不可再分的作业单位，其作业时间为确定值；作业元素在满足作业优先关系的前提下可被分配至任意工作站上，但任意作业元素都必须且只能分配至一个确定的工作站；作业元素的分配不受工作站约束，作业元素的作业时间不因工作站而不同；装配线的生产节拍不小于任意工作站时间；装配线上不存在并行工作站；装配线上所有工作人员的技能水平不存在差异，可完成任意工作站上的装配作业；不考虑生产过程中的空间、成本和资源等约束，忽略工作人员的行走路径时间等.

2) 目标函数.装配线平衡率最大化，即装配线上总的空闲时间最短，装配线生产效率更高，函数表达为

(1)

式中：M为工作站总数；N为装配线上所有作业元素的总数；CT为装配线的生产节拍；ti为装配线上第i个作业元素的作业时间.

装配线平滑指数最小化，即装配线上各工作站彼此间的工作负荷更为均衡，整体平衡性更佳，函数表达为

(2)

式中Tk为装配线上第k个工作站的作业时间.

总的目标函数F为

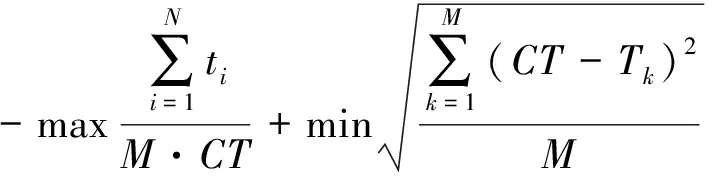
(3)

约束条件为

Sa∩Sb=Φ(a,b=1,2,…,M且a≠b)

(4)

(5)

Tk≤CTk=1,2,…,M

(6)

∀i，如果Pij=1,i∈Sa,j∈Sb，则a≤b

(7)

式中：Sa，Sb分别为装配线上工作站a和工作站b上所分配到的作业元素集合；S为装配线所有工作站上的作业元素集合；Pij=1表示i是j的紧前作业元素；i∈Sk(k=1,2,…,M)表示作业元素i在工作站k上完成.式(3)为装配线平衡优化的目标函数，由装配线平衡率和装配线平滑指数两部分共同组成；式(4)表示每一个作业元素只能分配至一个确定的工作站上；式(5)表示所有作业元素都将分配至装配线上的工作站；式(6)表示装配线的生产节拍不小于任意工作站时间；式(7)表示任一作业元素的分配都必须符合作业优先关系.

2 混合混沌粒子群算法设计

作为典型的NP组合优化问题，当前求解装配线平衡模型的算法主要有：遗传算法、模拟退火算法、蚁群算法、粒子群算法等，各类算法各具特点，但也都存在着各自的不足之处.粒子群算法具有概念简单，设定参数较少，便于实现等特点，但在寻优过程中也易发生“早熟”现象，陷入局部最优[8].因此，将模拟退火算法与混沌思想引入标准粒子群算法中，以三者融合后的混合混沌粒子群算法来求解装配线平衡模型.

基于NFL(No free lunch，简称NFL)定理，并不存在某一种算法面对所有求解问题都是最有效的，任何算法都有其所适宜的应用领域[9].因此，通过算法的混合来实现其适应域与优化性能的改善提升成为了较为有效的一种手段.考虑到装配线平衡问题及所建立的融合优化多目标函数模型的复杂性，以及粒子群算法所存在的不足与缺陷，故采用混合算法来进行问题的求解.

2.1 基本粒子群算法

粒子群算法(Particle swarm optimization，简称PSO)从本质上来说是一种基于仿生的迭代算法，通过运算过程中的反复迭代来寻求问题的最优解[10].粒子在每一次寻优迭代过程中通过比较两个“极值”来更新自身的速度与位置.个体极值为粒子自身当前寻找到的最优位置，其可以看作粒子自身的寻优经验；全局极值为整个群体当前寻找到的最优位置，其可以看作粒子种群的寻优经验.

设一个包含M个粒子的粒子群在D维空间中飞行，粒子i在D维空间中的飞行速度与位置表示为

(8)

(9)

2.2 混合混沌粒子群算法描述

虽然粒子群算法在求解过程中具有多项优势，但其对于算法的初始设值较为敏感及依赖，全局搜索效率较差，影响求解精度[11].因此提出将模拟退火算法与混沌思想引入粒子群算法中，借助混沌所具有的遍历性、随机性及规律性引入粒子速度的更新调整过程中，使系统表现出完全混沌特性；引入模拟退火算法，在一定范围内以变化的概率接受较差解，使其能有效跳出局部最优并抑制“早熟”现象，并采用基于适应度函数值与接受概率的初始化方法对模拟退火算法中的重要影响参数温度初始值进行初始化，进一步提升混合算法的搜索性能.融合后的混合混沌粒子群算法(Hybrid chaotic particle swarm optimization algorithm，简称H-CPSO)有效提升了算法求解的综合优化性能，可将其应用于装配线的平衡优化.图1为混合混沌粒子群算法的求解流程图.

图1 混合混沌粒子群算法流程图Fig.1 Hybrid chaotic particle swarm optimization algorithm flow chart

2.3 装配线平衡模型与算法的映射

装配线平衡问题为离散型的组合优化问题[12]，而H-CPSO算法不能直接运用于求解离散空间的组合优化问题，因此需要对混合算法以及平衡问题模型中的相关元素进行对应[13].求解空间中，每一个可行的作业序列定义为一个粒子，粒子的总数即种群规模，所有可行的作业序列集合构成了整个粒子群[14].

1)粒子速度.在n维解空间中，粒子速度vi=(v1,v2,…,vn)，粒子的初始速度由随机确定产生，并依据引入混沌思想的速度更新公式进行迭代更新.

2)粒子位置.粒子的位置对应于装配线上的一个作业序列，xi(k)为第i个粒子在第k次迭代时的位置.

3)粒子的适应度函数.多目标平衡模型以装配线平衡率与平滑指数为最优化目标，故适应度函数对应为给定工作站总数M的函数F，其表达为

(10)

2.4 求解装配线平衡模型的混合算法设计

1)编码与解码.为了将离散的编码序列与连续的粒子位置迭代进化相对应起来，选用随机数表示法来对粒子进行编码.其编码及解码的工作流程所述如下：

编码规则：采用随机数表示法对粒子进行编码.

编码过程：首先，对粒子的每一维度随机生成一组介于0～1之间的随机数，随机数的大小即为对应粒子的权重；然后，根据权重大小对粒子进行排序，并依序进行迭代计算.

解码规则：粒子位置中的各作业元素依据权重大小分配至若干工作站[15]，解码结果为输出一个工作站划分集合Dk={D1,D2,…,Dm}.

解码过程：选定一个新的工作站k，将其作业时间置零；在满足作业元素优先关系的情况下，将排序后随机数数值更大的作业元素i分配至工作站k，工作站k的作业时间Tk=∑ti，若Tk≤CT，则将作业元素i放置于工作站k内，否则返回上一步骤；若当前分配的作业元素为粒子位置中的最后一个作业元素，解码结束，否则返回上一步骤.

2)种群初始化.为确保H-CPSO算法中粒子群种群生产的多样性与合理性，综合运用随机生成任务序列法与位置权重法来完成种群初始化，通过随机选择任务分配至任务排列序列，并优先选择权重数值更大的任务[16].粒子群的生成以及粒子速度与位置的初始化计算式为

I={x10,x20,…,xm0}

(11)

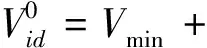
(12)

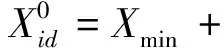
(13)

3)初始温度.初始温度是混合混沌粒子群算法全局优化搜索性能的重要影响参数，依据初始粒子群中最大目标函数值f(xi(0))max与最小目标函数值f(xi(0))min的差值以及初始接受概率pτ，计算初始温度TP0，其计算式为

TP0=(f(xi(0))min-f(xi(0))max)/lnpτ= -|Δf|/lnpτ

(14)

4)粒子的速度与位置更新.粒子速度与位置的更新，可在初始化速度与位置的基础上，依据迭代公式进行更新.对于粒子速度的更新，可在确定初始参数ω，c1，c2的情况下，将粒子自身最优位置所对应的随机数与当前位置所对应的随机数相减，同理将粒子全局最优位置所对应的随机数与当前位置所对应的随机数相减，分别与c1r1和c2r2做乘积，计算式如式(8)所述；同时采用混沌思想中的Logistic模型对粒子速度更新公式中的r1和r2进行混沌优化，其计算式为

ri(0)=random[0,1]

(15)

ri1(k)=ri2(k)=ri(k)

(16)

ri(k+1)=4ri(k)·(1-ri(k))

(17)

对于粒子位置的更新，公式可表述为将粒子当前位置对应的随机数与更新后速度所对应的随机数相加，得到的即为粒子更新后的位置所对应的随机数，其计算式如式(9)所述.

5)降温速率.H-CPSO算法中的退火过程采用线性降温方式，其计算式为

TPk+1=λ·TPk

(18)

3 计算实例

为了验证混合混沌粒子群算法对于装配线平衡问题的求解有效性，选用经典实例库中的MITCHELL问题，分别采用标准粒子群算法与混合混沌粒子群算法进行平衡模型求解，对比分析平衡优化效果.

3.1 参数设定

MITCHELL问题的作业顺序图如图2所示，分别求解装配线工作站数量为4～9个的6种情况.根据前期测试经验，综合考虑混合算法的求解精度、搜索性能以及运算效率等因素，混合混沌粒子群算法的参数设定为：种群规模m=40；惯性权重ω=0.9；学习因子c1=c2=2；初始接受概率pτ=0.8；最大迭代次数Gmax=300；降温速率λ=0.98.

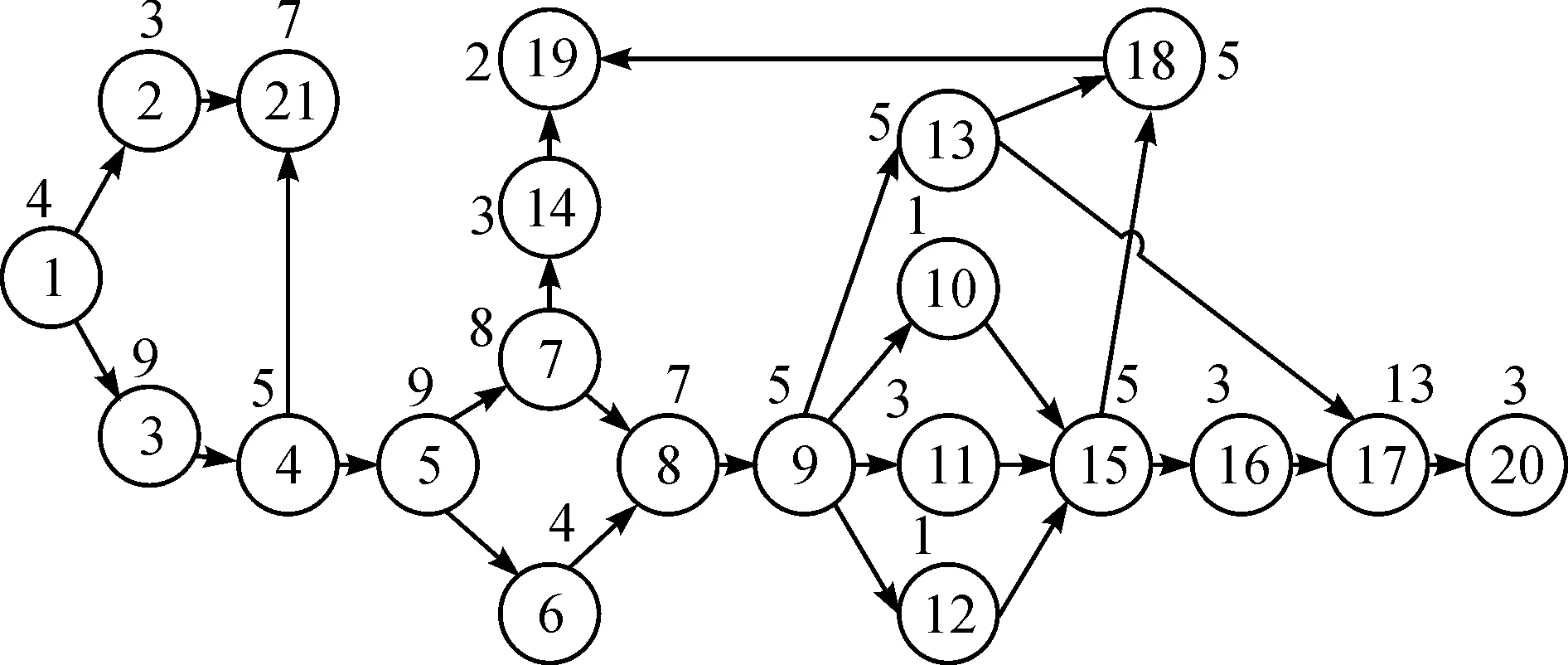
图2 MITCHELL问题作业顺序图Fig.2 Task sequence diagram of problem MITCHELL

3.2 实例计算结果分析

在装配线工作站数量分别为4～9个的6种情况下，求得采用标准粒子群算法与混合混沌粒子群算法的装配线作业分配方案，求解结果对比见表1.

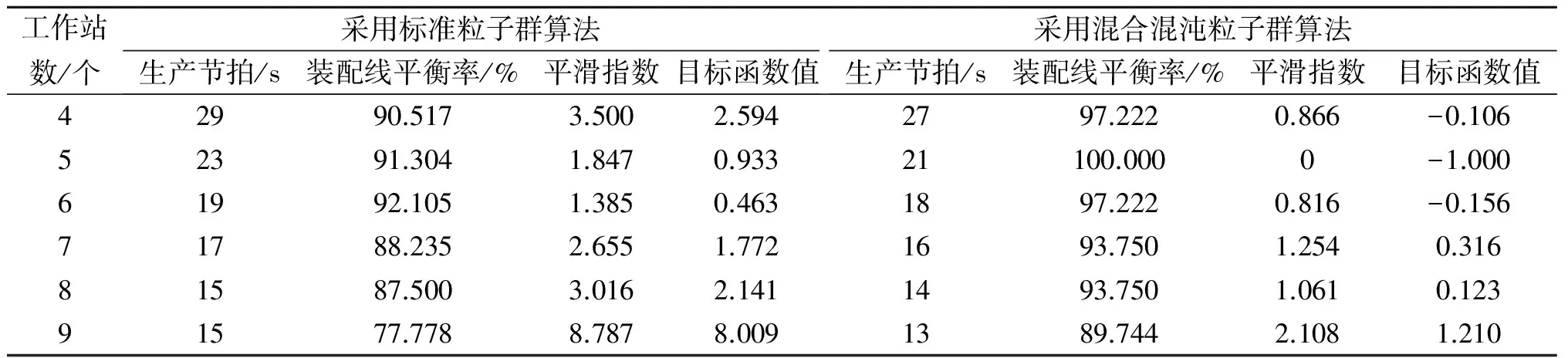
表1 MITCHELL问题求解结果对比

从表1中可以看到：不论何种工作站数量下，混合混沌粒子群算法所对应的目标函数值均小于标准粒子群算法所对应的目标函数值，说明混合算法对于装配线的平衡优化效果优于标准粒子群算法，进一步验证了混合混沌粒子群算法对于求解装配线平衡问题具有较为理想的效果.

4 结 论

针对装配线平衡问题，将衡量装配线是否最优化的多项参考指标进行融合优化，以装配线平衡率与平滑指数最优化为目标函数建立多目标装配线平衡模型.在标准粒子群算法的基础上，利用混沌所特有的遍历性、随机性以及规律性和模拟退火算法的全局寻优特点，设计三者相融合的混合混沌粒子群算法；并运用混合算法求解装配线的平衡优化模型.计算实例结果表明，所设计的混合混沌粒子群算法对比标准粒子群算法具有更佳的全局寻优能力，效率与可靠性进一步提升，对于装配线平衡问题具有较好的求解效果.

[1] DRISCOLL J, THILAKAWARDANA D. The definition of assembly line balancing difficulty and evaluation of balancing solution quality[J]. Robotics and computer integrated manufacturing，2001，12(5)：81-86.

[2] SCHOLL A, KLEIN R. SALOME：a bi-direction branch-and-bound procedure for assembly line balancing[J]. Informs journal of computing，1997，9(4)：319-334.

[3] MCMULLEN P. R, FRAZIER G.V. Using simulated annealing to solve a multi objective assembly line balancing problem with parallel workstations[J]. International journal of production research，1998，36(10)：2717-2741.

[4] 彭慧，徐克林，侣占华，等.采用遗传算法的混流装配线平衡多目标优化[J].现代制造工程，2011(11)：49-53.

[5] 刘炜琪，刘琼，张超勇，等.基于混合粒子群算法求解多目标混流装配线排序[J].计算机集成制造系统，2011，17(12)：2590-2598.

[6] 李明，张则强，刘济洲，等.变异粒子群算法在装配线平衡问题中的应用[J].组合机床与自动化加工技术，2014，16(10)：27-33.

[7] 陈勇，章金红，鲁建厦，等.基于GA-TS混合算法的多装配线调度建模[J].浙江工业大学学报，2013，41(4)：355-359.

[8] 刘海江，汤伟，张含叶，等.基于改进粒子群算法求解第二类装配线平衡问题[J].中国工程机械学报，2014，12(6)：508-513.

[9] 陈志杨，刘妍.改进粒子群搜索的二维皮革排样优化算法[J].浙江工业大学学报，2015，43(5)：492-496.

[10] 鲁建厦，胡海芬，董巧英，等.基于博弈粒子群算法的混流混合车间调度研究[J].浙江工业大学学报，2015，43(4)：398-404.

[11] 张则强，余庆良，胡俊逸，等.随机混流装配线平衡问题的一种混合粒子群算法[J].机械设计与研究，2013，29(2)：60-63.

[12] MOHD F. R, WINDO H. A review on assembly sequence planning and assembly line balancing optimization using soft computing approaches[J]. The international journal of advanced manufacturing technology，2012，59(1)：335-349.

[13] SENER A，ADIL B. Modeling and solving mixed-model assembly line balancing problem with setups. Part I: a mixed integer linear programming model[J]. Journal of manufacturing systems，2014，33(1)：177-187.

[14] SENER A. Performance evaluation of ant colony optimization-based solution strategies on the mixed-model assembly line balancing problem[J]. Engineering optimization，2014，46(4/6)：842-862.

[15] ALENA O，CHRISTIAN O. How to design effective priority rules: example of simple assembly line balancing[J]. Computers & industrial engineering，2014，69：43-52.

[16] GEMA C，ALBERT C. Combining matheuristics and MILP to solve the accessibility windows assembly line balancing problem level 2 (AWALBP-L2)[J]. Computers & operations research，2014，48：113-123.

(责任编辑：刘 岩)

Research on assembly line balancing problem based on hybrid chaotic particle swarm optimization algorithm

LU Jiansha, ZHU Kai, DONG Qiaoying

(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

In order to achieve the multi objective optimization of assembly line balancing, a multi objective assembly line balancing model was constructed with the objectives of maximization of assembly line balancing rate and minimization of smoothing index. The particle swarm optimization algorithm tends to be “premature” and falls into the local optimum. So the simulated annealing algorithm and chaos theory are introduced, a hybrid chaotic particle swarm optimization algorithm with three phase fusion was designed. The characteristics of ergodic, stochastic and regularity of chaos was used to intervene the particle velocity updating and adjustment. The simulated annealing algorithm was adopted to inhibit the “premature” phenomenon, an example was given to verify the model and algorithm, and the results prove the method is effective.

assembly line balancing; fusion optimization; simulated annealing; chaos; particle swarm optimization algorithm

2016-05-16

鲁建厦(1963—)，男，浙江余姚人，教授，博士生导师，研究方向为精益生产、生产调度和制造业信息化，E-mail：ljs@zjut.edu.cn.

TB491

A

1006-4303(2017)01-0114-05