感悟数学思想积累活动经验

刘延革　王雅薇

教学内容：人教版数学六年级上册第107～108页。

教学目标：

（1）在探究图形和数的问题中，使学生发现数与形之间的联系，体会数形互助解决问题的方法。

（2）在观察、发现、猜想、推理等数学活动中，帮助学生积累数形结合思考问题的经验，渗透归纳推理和极限思想。

（3）体会数形结合思想在学习和生活中的广泛应用，感受数形结合的价值，初步形成数形结合的意识。

教学过程：

一、谈话导入

师：同学们，一提到数学你们就会想到什么？

生1：我会想到数，如0、1、2、3等自然数，0.1、2.5等小数。

生2：我会想到“加、减、乘、除”等运算符号。

生3：我会想到如何进行运算、有趣的数学问题等。

生4：我会想到三角形、长方形、正方形、平行四边形等几何图形。

师：如果把同学们说的这些知识进行分类，可以分成两类。一类是由数、运算符号、运算方法组成的“数”；另一类是由点、线、面、体组成的“形”。“数”和“形”是数学研究的两大类对象。“数”和“形”有没有关系呢？

生1：有关系，如圆这个图形和π有关系。

生2：我没有想过这个事情。

师：大多数同学没有想过“数”与“形”之间的关系，今天我们就来研究。（板书：数与形）

评析：从学生学习过的数学知识入手，引导学生回忆数学研究的两个重要领域——数与代数领域和空间与图形领域，以“‘数和‘形之间有没有关系”这一问题为突破口，引发学生思考，有效地调动了学生思维的积极性，激发了他们学习本节课的兴趣。

二、体会形中有数，数中有形

1.例1教学

课件出示：

师：你发现图形的规律了吗？（学生观察）按照规律第四个图形应该是什么样子的？

评析：教师没有直接把四幅图一并出示，而是逐次出现。目的是给学生时间，让学生感受变化，在体会变化中发现规律，根据规律想象出圖形，既培养了学生的空间想象能力，又为将图形与算式建立联系做好准备。

生：如果把每个小正方形的边长看作是“1”，第四个图形应该是边长为4的大正方形。

课件出现：

师：你能用数或式子表达你发现的规律吗？

（学生思考、表达、汇报）

作品一：1、4、9、16

师：你能明白每个数表示的意思吗？

生：第一个有1个正方形，第二个有4个正方形，第三个有9个正方形，第四个有16个正方形。

作品二：1×1、2×2、3×3、4×4

问：这些算式是什么意思？

生：1是边长，1x1是第一个图形的面积；2×2、3×3、4×4分别表示图形的面积。

作品三：1、1+3、1+3+5、1+3+5+7

问：什么意思？

学生解释算式中每个数字在图形中的位置。如下图：

师：同一个图形，观察出的规律不一样，每个规律是从什么角度观察的？

生：作品一观察的是图形中小正方形的总个数，作品二观察的是图形的边长与面积的关系，作品三反映的是围绕左下角的正方形，外圈的正方形数逐渐增加。

师：虽然观察角度不同，但是我们都能从图形中找到算式中的数。

评析：教师为学生提供了充分的时间和空间，放手让学生自主观察、探究，多次安排从图形中找数，旨在让学生深刻感受到形中蕴含着数，为学生理解数形结合奠定了坚实的基础。教师及时获取学生的信息，并对学生的信息进行了分类、分层处理，处处紧扣“数”与“形”的结合。

2.算式1+3+5+7+9+11+13对应的图形

师：如果沿着“1+3+5+7”这个规律继续往下想，1+3+5+7+9+11+13这个式子对应的图形是什么样子7

生：我是用数的方法。一共7个数相加，所以边长是7。

师：谁理解他的意思了，到图形上给大家数一数，7指的是哪？（学生到黑板上指图形说明）

师：那么，1+3+5+7+9+11+13+15+17+19这个算式对应的图形又是什么样子？

课件验证：

1+3+5+7+9+11+13

师：如果1+3+5+7+9+11+13+15+17+19对应的图形是什么？

生：对应的图形是边长为10的正方形。

师：为什么？

生：10个数相加。

3.小结

师：回顾我们研究的过程，我们从图中找到数，又在数中想到了形，数与形有着紧密的关系。

评析：给算式想图形的样子，旨在让学生感受数的规律也能用图形表示出来，随着数的个数逐渐增加，培养了学生的推理能力和空间想象能力。小结前一段的学习时，教师没有把着力点放在“规律”的总结上，而是重点让学生感受数与形的关系，进一步加强学生对“数中有形，形中有数”的理解与体会。

三、体会以形助数、以数解形，数形互助

1.体会以形助数

出示：

师：省略号是什么意思？

生：省略号表示一直加下去，有无数个。

师：猜测一下和是多少？（学生有些迷茫，不知道和是多少）的微妙之处。

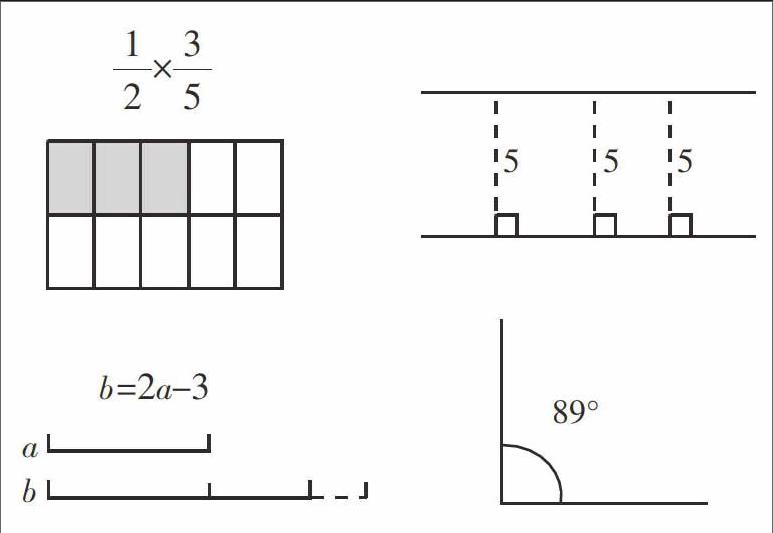
3.出示以前学习中数形互助的例子

课件出示：

评析：借助学生已有的知识经验和学习素材，进一步感受图形的直观特点和数精确、精准的特点，提升对以往学习的认识高度，进一步理解、体会数形结合的好处。

师：数和形的关系非常密切，它们各有各的优势，数和形有机结合才能更好地帮助我们解决问题。

四、深入体会“数无形时少直观，形无数时难入微”

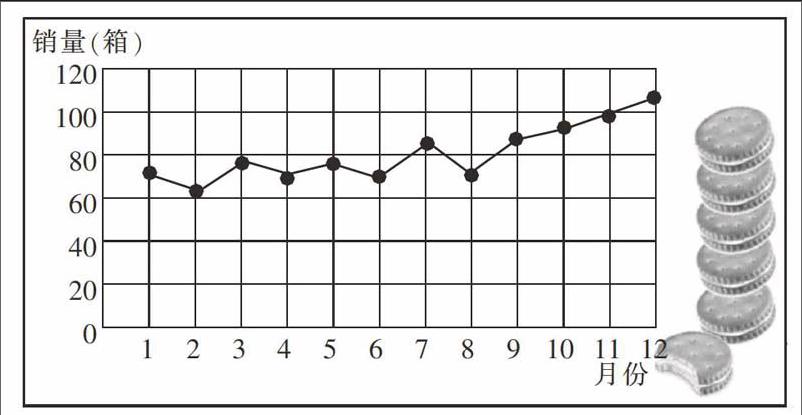
（出示：超市2014年销售某种饼干的数量）

1.以形助数，解决生活中的销售问题

课件出示：

月份：一 二 三 四 五 六 七 八 九 十 十一 十二

销量：72 62 79 68 77 69 82 71 89 89 99 105

师：这是某种饼干2014年的销售量，超市下一年是否还继续进货这种饼干？

生：进吧（个别）。

师：如果把这些数据制成折线统计图，你们再来感受一下。

课件出示：

生：进！（齐声，坚定）因为销售量越来越多，是上升的趋势！

师：在解决这个问题的时候，是谁帮助了谁呢？生：图在帮助数！（齐答）

2.以数解形，解决生活中的运输问题

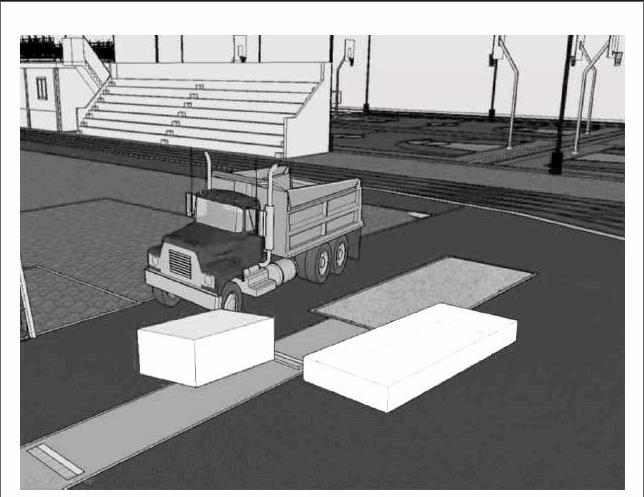
课件出示：

师：如果这样一辆卡车，想把这个沙坑里的沙子拉走，能不能一次性把沙子全部拉完呢？我们把车厢的形状和沙坑里的形状提取出来，同学们判断一下。

生：（集体沉默2、3秒钟）不知道！老师能给我们具体数据吗？

课件出示：车厢长2.5，宽4，高1.5；沙坑长3，宽7，深0.7。

生：能拉走！车厢的容积是15，沙坑的容积是14.7。

师：解决这个问题时，谁帮了谁？

生：数帮了形。

师：同学们思考一下，在数与形互助的過程中，数的优势是什么？形的优势是什么？

生：数是准确的，形一目了然。

师：“数”能更精准地表达，“形”能更直观地表达事物。其实，华罗庚老爷爷很早就说过这样一句话：“数缺形时少直观，形少数时难入微。”你能理解其中的含义吗？

生：只有数没有形，看不出来；只有形没有数，难算出来。

师：难算出来就是不具体，不能精确地表达！所以后面还有一句话，同学们读一读。

生：数形结合百般好，隔离分家万事休。

师：对！如果把数、形分家什么事都做不来。

评析：借助生活中的两个典型素材，再一次让学生体会数和形各自的特点，形能直观呈现数的抽象。数能精确描述形的模糊，深刻理解华罗庚先生关于数形结合的经典之词。

总评：

本节课围绕数形结合，选择适当的教学内容，设计了一系列的数学活动，帮助学生亲历活动过程，在活动中渗透数学思想方法，积累基本活动经验。具体如下：

1.利用学生的好奇心，激发学习兴趣

本节课开始部分，教师引导学生回顾数学学习的重要内容“数与代数”和“几何图形”，进而抽象出“数”与“形”。因为学生学习这两个领域时是分别进行的，很少有学生能够把两者联系起来，这与学生的思维习惯形成了强烈的矛盾反差，于是引发了学生的好奇心，激发了学生思考的兴趣。

2.整体把握教学内容，凸显数形结合的思想

本节课安排了两个例题，例1引导学生从图形中发现“数”，通过数想象图形，凸显“形中有数”“数中有形”的关系。例2引导学生利用图形解决计算问题，以及“以数解形”的妙处，进一步体会“数形互助”的关系。教学中教师还补充了大量数形结合的实例，如统计图描述数据，数据描述沙坑、车厢的大小等。这些素材很好地诠释了华罗庚先生所说：“数缺形时少直观，形少数时难入微：数形结合百般好，隔离分家万事休。”

3.核心活动设计为学生积累了数学思考经验

本节课通过两个核心活动，一是让学生看图写数，看数想形；二是让学生借助图形和数的推理来完成计算。在这两个活动中，每个学生有自己独立思考的空间和时间，不断经历观察、猜测、抽象、概括的过程，还经历了想象、推理、解释的过程。在组织学生汇报交流中，教师也给予每个学生展示思维过程的权利，促进了学生活动经验的不断提升。

4.教师尊重学生，促进了辩证唯物主义世界观的形成

教学中教师尊重学生的思维习惯和现状，允许学生对极限思想的暂时不理解，引导学生从“以形助数”和“以数解形”两个侧面体会“数形结合”的思想，并把这种观点延伸到自然界中事物之间的联系，有效地促进了学生用辩证唯物主义观点看待事物的思想方法的形成。