Spectra of the Edge-Subdivision-Vertex and Edge-Subdivision-Edge Coronae

LU Peng-li,XUE Liang-yuan

(School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China)

Spectra of the Edge-Subdivision-Vertex and Edge-Subdivision-Edge Coronae

LU Peng-li,XUE Liang-yuan

(School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China)

In this paper two classes of corona are defined:edge-subdivision-vertex coronaG1∨G2and edge-subdivision-edge coronaG1∀G2.Then,theA-spectrum (respectively,L-spectrum,Q-spectrum) of the two classes of new graphs are given in terms of the corresponding spectra ofG1andG2.By using the Laplacian spectra,the number of spanning trees and Kirchhoff index ofG1∨G2andG1∀G2are obtained.

spectrum; edge-subdivision-vertex corona; edge-subdivision-edge corona; spanning tree; Kirchhoff index

LetG=(V,E) be a graph with vertex setV={v1,v2,…,vn} and edge setE.The adjacency matrix ofGis denoted byA.The Laplacian matrix ofGis defined asL=D-A.Denote the eigenvalues ofLbyμ1(G)≥μ2(G)≥…≥μn(G).The signless Laplacian matrix ofGis defined asQ=D+A.For a graphG,we callfA(respectively,fL,fQ) the adjacent (respectively,Laplacian,signless Laplacian ) characteristic polynomial ofG[1-3].Calculating the spectra of graphs as well as formulating the characteristic polynomials of graphs is a fundamental and very meaningful work in spectral graph theory.

The subdivision graphS(G)[3]of a graphGis the graph obtained by inserting a new vertex into every edge ofG.We denote the set of such new vertices byI(G).

Definition 1 The edge-subdivision-vertex corona of two vertex-disjoint graphsG1andG2,denoted byG1∨G2,is the graph obtained fromG1and |E(G1)| copies ofS(G2) with each edge ofG1corresponding to one copy ofS(G2) and all vertex-disjoint,by joining end-vertex of theith edge ofE(G1) to each vertex ofV(G2) in theith copy ofS(G2).

Definition 2 The edge-subdivision-edge corona of two vertex-disjoint graphsG1andG2,denoted byG1∀G2,is the graph obtained fromG1and |E(G1)| copies ofS(G2) with each edge ofG1corresponding to one copy ofS(G2) and all vertex-disjoint,by joining end-vertex of theith edge ofE(G1) to each vertex ofI(G2) in theith copy ofS(G2).

The paper is organized as follows.In section 1,some lemmas used in this paper are given.In section 2,theA-spectrum (respectively,L-spectrum,Q-spectrum) of edge-subdivision-vertex coronaG1∨G2for an regular graphG1and an regular graphG2(see Theorems 1,2,3) are computed.In section 3,theA-spectrum (respectively,L-spectrum,Q-spectrum) of edge-subdivision-edge coronaG1∀G2for an regular graphG1and an regular graphG2(see Theorems 4,5,6) are obtained.By Theorems 2 and 5,the number of spanning tree and Kirchhoff index ofG1∨G2andG1∀G2(see Corollaries 2,3,5,6) are obtained.

1 Some Lemmas

Lemma 1[4-5]TheM-coronalΓM(x) of a square matrixMis defined to be the sum of the entries of the matrix (xIn-M)-1,that is,

(1)

where 1ndenotesthecolumnvectorofsizenwithalltheentriesequal1.

Lemma 2[6]LetM1,M2,M3andM4be respectivelyp×p,p×q,q×pandq×qmatrices withM1andM4invertible.Then

(2)

(3)

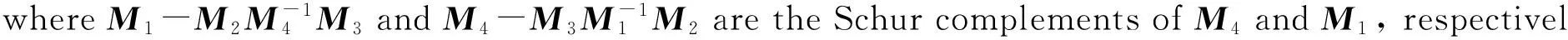
Lemma 3[7]The Kronecker productA⊗Bof two matricesA=(aij)m×nandB=(bij)p×qis themp×nqmatrix obtained fromAby replacing each elementaijbyaijB,

A⊗B=(aijB)mp×nq.

(4)

Lemma 4[2]Lett(G) denote the number of spanning tree ofG,it is well known that ifGis a connected graph onnvertices with Laplacian spectrumμ1(G)≥μ2(G)≥…≥μn-1(G)>μn(G)=0,then

(5)

TheKirchhoffindexofagraphG1,denotedbykf(G),isdefinedasthesumofresistancedistancesbetweenallpairsofvertices[8].Gutmanetal.[9]provedthattheKirchhoffindexofaconnectedgraphn1withn(n≥2)vertices.

Lemma 5[9]The Kirchhoff index of a connected graphGwithn(n≥2) vertices can be expressed as

(6)

2 Spectra of Edge-subdivision-vertex Corona

2.1A-spectrum of edge-subdivision-vertex corona

Theorem 1 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

Proof LetA1denote the adjacency matrices ofG1.Then,with respect to the partitionV(G1)∪[U1∪U2∪…∪Un2]∪[E1∪E2∪…∪Em2] ofV(G1∨G2),the adjacency matrix ofG1∨G2can be written as

where 0s×tdenotesthes×tmatrixwithallentriesequaltozero,Inis the identity matrix of ordern,1mdenotes the column vector of sizemwith all the entries equal one.Thus the adjacency characteristic polynomial ofG1∨G2is given by

where

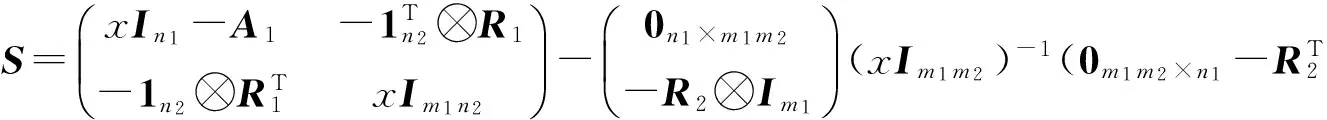
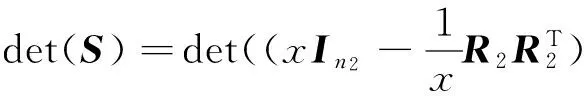
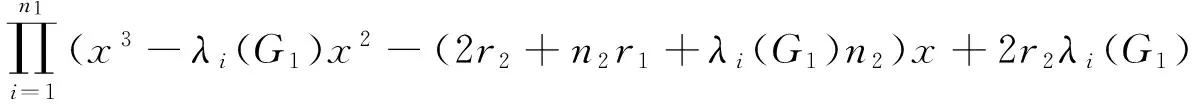
2.2 L-spectrumofedge-subdivision-vertexcorona

Theorem 2 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

Proof LetR1,R2be the incidence matrix ofG1andG2respectively.LetL1denote the Laplacian matrices ofG1.Then,the Laplacian matrix ofG1∨G2can be written as

Thus the Laplacian characteristic polynomial of G1∨G2isgivenby

where

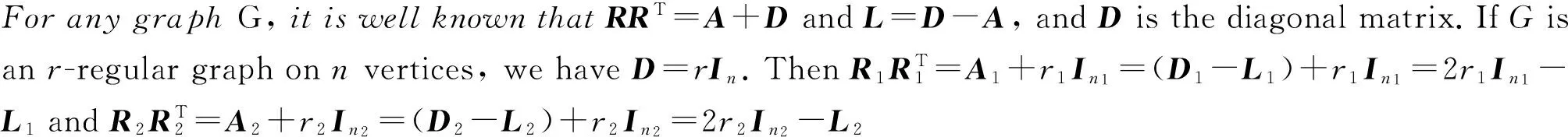
Corollary 1 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then the Laplacian spectrum is

(a) 2，repeatedm1m2-m1n2times;

(b) Two roots of the equationx2-(4+r2)x+4=0,for each root repeatedm1-n1times;

(c) Two roots of the equationx2-(4+r2)x+2r2+μi(G2)=0,for each root repeatedm1times,fori=2,…,n2;

(d) Three roots of the equation

x3-(4+r2+r1n2+μi(G1))x2+(4+(2+r2)n2r1+(4+r2+n2)μi(G1))x-(4+2n2)μi(G1)=0,

fori=2,…,n1.

Corollary 2 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

Corollary 3 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

2.3Q-spectrum of edge-subdivision-vertex corona

Theorem 3 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

Proof The proof is similar as Theorem 2 and is omitted.

3 Spectra of Edge-subdivision-edge Corona

3.1A-spectrum of edge-subdivision-edge corona

Theorem 4 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

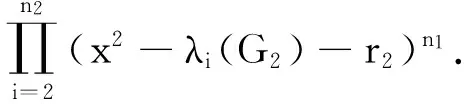
Proof The adjacency matrix ofG1∀G2can be written as

Thus the adjacency characteristic polynomial of G1∀G2isgivenby

where

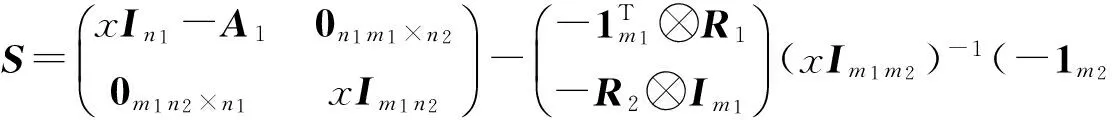
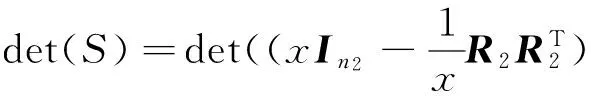
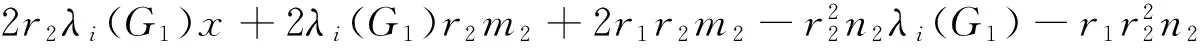
3.2L-spectrum of edge-subdivision-edge corona

Theorem 5 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

Proof The Laplacian matrix ofG1∀G2can be written as

Thus the Laplacian characteristic polynomial of G1∀G2isgivenby

where

Corollary 4 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then the Laplacian spectrum is

(a) 4，repeatedm1m2-m1n2-n1times;

(b) Two roots of the equationx2-(4+r2)x+2r2=0,for each root repeatedm1-n1times;

(c) Two roots of the equationx2-(4+r2)x+2r2+μi(G2)=0,for each root repeatedm1m1m1times,fori=2,…,n2;

(d) Four roots of the equation

x4-(8+r2+r1m2+μi(G1))x3+(16+6r2+(6+r2)r1m2+(8+r2+m2)μi(G1))x2-

Corollary 5 LetG1be anr1-regular graph onn1vertices andm1edges,andG2anr2-regular graph onn2vertices andm2edges.Then

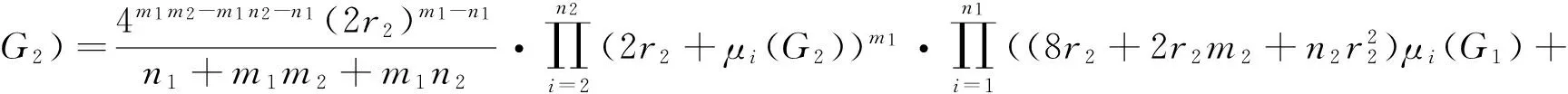
(4m2-2n2r2)r1r2);

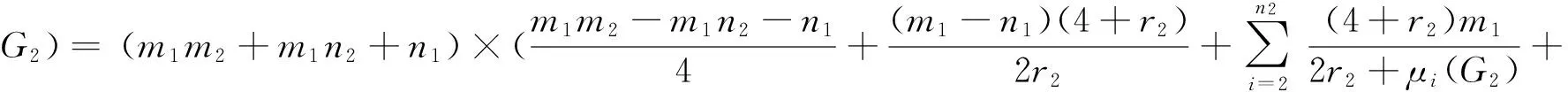
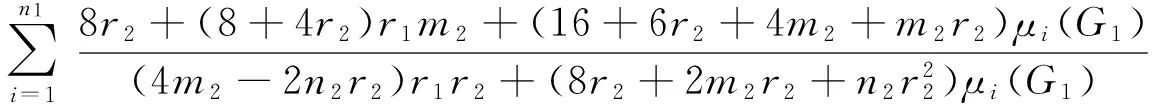
3.3Q-spectrum of edge-subdivision-edge corona

Theorem 6 LetG1be anr1-regular graph onn1vertices,andG2anr2-regular graph onn2vertices andm2edges.Then

Proof The proof is similar as Theorem 5 and is omitted.

[4] MCLEMAN C,MCNICHOLAS E.Spectra of coronae[J].Linear Algebra Appl,2011,435(5):998-1007.

[5] CUI S Y,TIAN G X.The spectrum and the signless Laplacian spectrum of coronae[J].Linear Algebra Appl,2012,437(7):1692-1703.

[6] ZHANG F.The Schur complement and its applications[M].New York:Springer,2006.

[7] HORN R A,JOHNSON C R.Topics in matrix analysis[M].Cambridge:Cambridge University Press,1991.

[9] GUTMAN I,MOHAR B.The quasi-Wiener and the Kirchhoff indices coincide[J].J Chem Inform Comput Sci,1996,36(5):982-985.

(编辑 HWJ)

2016-01-10

国家自然科学基金资助项目(11361033)

O175.6

A

1000-2537(2017)01-0084-07

边剖分点冠图和边剖分边冠图的谱

卢鹏丽*,薛亮元

(兰州理工大学计算机与通信学院，中国 兰州 730050)

定义两个图G1和G2的冠图：边剖分点冠图G1∨G2和边剖分边冠图G1∀G2；并用原图的邻接谱、拉普拉斯谱、无符号拉普拉斯谱表示两类冠图的邻接谱、拉普拉斯谱、无符号拉普拉斯谱.基于拉普拉斯谱，给出并证明两类冠图G1∨G2和G1∀G2的生成树数目以及Kirchhoff指数.

谱；边剖分点冠图；边剖分边冠图；生成树；Kirchhoff指数

10.7612/j.issn.1000-2537.2017.01.013

* 通讯作者,E-mail：lupengli88@163.com