轮边电机驱动型电动汽车动力系统参数优化设计
2017-02-28龚贤武唐自强许世维贺伊琳
龚贤武, 唐自强, 赵 轩, 许世维, 贺伊琳
(1.长安大学 电子与控制工程学院,陕西 西安 710064; 2.长安大学 汽车学院,陕西 西安 710064)
轮边电机驱动型电动汽车动力系统参数优化设计
龚贤武1, 唐自强2, 赵 轩2, 许世维2, 贺伊琳2
(1.长安大学 电子与控制工程学院,陕西 西安 710064; 2.长安大学 汽车学院,陕西 西安 710064)
文章对轮边电机驱动型电动汽车动力传动系统参数进行了优化设计。依据行驶工况高频车速区间与电机高效区域相重合的原则以及满足整车性能指标的要求,引入工况加权因子,对轮边电机和蓄电池参数进行了匹配;以整车动力性指标为约束、整车加权工况平均能量消耗最小为目标,分别采用粒子群算法(particle swarm optimization,PSO)和遗传算法(genetic algorithm,GA)对固定挡速比进行了优化设计;并基于Matlab/Simulink搭建的整车性能仿真平台,对整车性能进行了仿真分析。仿真结果表明,整车性能均能满足设计要求;通过与以单循环NEDC工况能耗最小为目标的速比优化结果的对比,表明以加权工况平均能耗最小为目标的速比优化设计方法能够兼顾不同工况下能耗经济性,具有较好的适用性。
电动汽车;轮边驱动;参数匹配;速比优化;智能算法
目前研发的电动汽车仅在传统汽车结构的基础上改装而成,并没有发挥电机驱动拥有的技术优势[1]。而轮边电机驱动型电动汽车是一种有别于传统汽车结构的新型电动汽车,其中轮边电机通过固定挡减速器和半轴直接驱动车轮,因此每个车轮转矩和转速由各电机控制器独立控制[2]。相比于传统汽车和集中式驱动电动汽车,轮边电机驱动型电动汽车省去了变速器、传动轴、变速驱动桥等部件,各驱动车轮的独立控制使得整车的动力性、操纵稳定性、车辆空间利用率以及制动能量回收均得到有效提升[2-3]。相比于轮毂电机驱动型电动汽车,轮边电机驱动型电动汽车可以将簧下质量转移到车身,因此车辆的操纵稳定性更优;同时轮胎磨损情况、电机安装以及维修调试方便性方面也更优,因此产品更适合应用[4]。
当前,轮边电机驱动型电动汽车的研究热点主要集中在电子差速以及驱动控制等方面[3,5-6],而对轮边电机驱动型电动汽车参数匹配的研究较少。文献[1]依据整车性能指标对两后轮独立轮毂电机驱动型电动汽车的轮毂电机和蓄电池参数进行了匹配;文献[2]对轮边电机驱动型电动汽车的驱动电机进行了选型与匹配,但没有对动力传动系统其他部件进行匹配;文献[7-8]依据整车性能指标对纯电动汽车传动系统参数进行了初步匹配,并基于智能优化算法,在单一工况下对传动系统部件参数进行优化设计。然而上述文献在对驱动电机参数匹配的过程中,没有考虑不同工况高频车速区间与电机高效区域相重合的原则,仅仅以单一循环工况消耗最少为目标对传动系统部件参数进行优化,不能有效地检验整车在其他工况下运行时的适应性。
本文针对一款前轮轮边电机驱动型电动汽车的传动系统,分析了以加权工况高频车速区间与电机高效区域相重合为原则、以满足整车性能指标为要求的轮边电机和电池参数的匹配方法;提出了整车加权工况平均能耗最小为目标、动力性为约束的2种智能优化算法的固定挡速比优化设计方案;基于Matlab/Simulink搭建整车性能仿真平台,对整车性能进行了仿真分析;并通过与以单循环NEDC工况能耗最小为目标的速比设计方案的对比,验证了本文提出的速比设计方案的有效性。
1 整车驱动系统、参数及性能指标
前轮轮边电机驱动型电动汽车的动力传动系统结构如图1所示,驱动电机通过固定挡速比减速器、半轴将动力传递至车轮。通常情况下驱动电机峰值转矩越大,整车动力性越好,然而电机峰值转矩增加会使电机尺寸与质量增加,反而影响整车经济性,同时带来车辆成本的增加[9]。因此,通常设置一级或两级齿轮的固定挡减速器来降低对驱动电机峰值转矩的需求。某前轮轮边电机驱动型电动汽车的基本参数与性能指标见表1所列。

图1 动力传动系统构型

参 数数 值整备质量+附加质量/kg1500汽车风阻系数0.335汽车迎风面积/m22.1汽车最高车速/(km·h-1)120百公里加速时间/s<15最大爬坡度/%28爬坡车速/(km·h-1)2060km/h匀速续驶里程/km>120
2 轮边电机及蓄电池参数匹配
2.1 轮边电机参数匹配
轮边电机的额定参数代表着电机的高效工作点,对整车经济性有重要影响,而其峰值参数对整车动力性也有重要影响。
2.1.1 轮边电机额定参数匹配
轮边电机实际工作点与整车经济性有直接关系,而电机额定参数是电机高效率区间,同时电机实际工作点决定于电动汽车的行驶工况,因此,在目前电动汽车电池技术尚未取得有效突破的情况下,结合电动汽车的行驶工况,使工况高频车速区间与电机额定参数相重合是提高整车能耗经济性的有效方法。但当前还没有针对电动汽车专用的行驶工况出现,因此本文仍使用传统燃油汽车的行驶工况。另外,因为不同行驶工况所对应的车速-时间历程不同,所描述车辆的行驶状态也不同,且电动汽车的实际行驶状态复杂多变,很难用单一工况来表征,所以本文选取具有代表性的3种循环工况,即欧洲NEDC循环工况、美国UDDC循环工况以及日本JC08循环工况。这3种工况的高频车速区间见表2所列,通过设定不同工况加权因子σ,对轮边电机额定参数进行匹配。
(1)
其中,VN-h为引入工况加权因子后的车辆高频车速区间;σ1为NEDC工况加权因子,值为0.5;σ2为UDDC工况加权因子,值为0.3;σ3为JC08工况加权因子,值为0.2;VNEDC-h为NEDC工况高频车速区间;VUDDC-h为UDDC工况高频车速区间;VJC08-h为JC08工况高频车速区间。
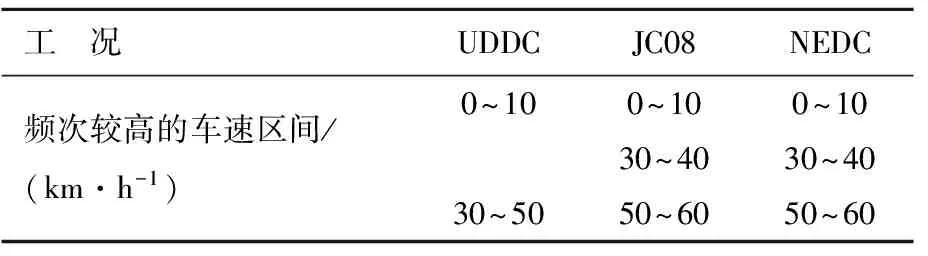
表2 不同工况的车速分析
由表2可知车速高频区间主要分为低速高频区间与中速高频区间,由(1)式可知车辆中速高频车速区间为35~47km/h。当车轮滑移率为10%时,轮边电机额定转速nnom为:
(2)
其中,unom为车辆高频车速区间;i为固定挡减速器速比;R为车轮半径,其值为0.282 m;根据10%车轮滑移率下车辆最高行驶车速需求,可知固定挡减速器速比i范围为:
(3)
其中,nmax为电机最高转速,其值为8 500 r/min;uamax为汽车最高车速。
由(3)式可知,i≤6.778,初选i为6.700,代入(2)式,可知电机额定转速范围为2 451~3 291 r/min。本文选择轮边电机额定转速nnom为3 000 r/min。根据整车最高车速行驶的功率需求,确定轮边电机额定功率Pe为:
(4)
其中,ηT为传动效率,其值为0.97;f为滚动阻力系数,其值为0.01;Cd为汽车风阻系数;A为汽车迎风面积;m为整备质量和附加质量。
由(4)式解得电机额定功率Pe为10.76 kW,因此电机额定转矩Te为:
Te=9 550Pe/nnom
(5)
由(5)式可以得到,电机的额定转矩Te为34.25 N·m。
2.1.2 轮边电机峰值参数匹配
依据整车性能指标最高车速、最大爬坡度和百公里加速时间来匹配轮边电机峰值功率[10]。
车辆以最高车速行驶时,轮边电机输出功率Pe1应满足:
(6)
车辆以最低稳定车速爬坡时,轮边电机输出功率Pe2应满足:
(7)
(8)
车辆百公里加速时间要求下,轮边电机输出功率Pe3应满足:
(9)
(10)
其中,δ为汽车旋转质量换算系数,值为1.01;vf为百公里加速末时刻车速,其值为100 km/h;vb为电机额定转速对应的车速,其值为47.6 km/h。
轮边电机峰值功率应同时满足以上3种整车性能指标要求,因此Pmax=max(Pe1,Pe2,Pe3)=27.5 kW,电机峰值转矩Tmax为:
(11)
由(11)式可得Tmax为87.54 N·m。
2.2 电池参数匹配
蓄电池作为电动汽车唯一的能量源,其性能参数决定了整车续驶里程和整车动力性能能否正常发挥。本文选取单体标称容量为45 A·h、额定电压为3.2 V的磷酸铁锂电池[10]。蓄电池参数需要同时满足轮边电机峰值功率和整车设计续驶里程的需求,通常情况下,当满足续驶里程需求时即可满足峰值功率需求,因此单体电池组数N为:
(12)
其中,P为60 km/h匀速行驶时功率需求,其值为4.58 kW;S为60 km/h匀速续驶里程;v为车速,其值为60 km/h;Ub为单体电池工作电压,其值为3.2 V;Db为电池放电深度,其值为0.8;Cb为单体电池容量,其值为45 A·h;η1为电池化学能与车辆动能之间的转换效率,其值为0.912;η2为车辆其他附属部件的能耗比例,其值为0.95。由(12)式可得单体电池组数N为92组。
3 固定挡速比优化设计
当轮边电机、蓄电池参数以及整车控制策略确定后,固定挡速比参数是决定整车动力性和经济性的唯一因素[8]。初选固定挡速比i为6.7,然而在该传动比下无法确保电动汽车不同行驶工况下始终处于能耗最优,因此有必要对固定挡速比进行优化设计。因为当前电动汽车续驶里程的提高比整车动力性的提高更为重要,所以本文以整车动力性指标为约束,在循环工况加权因子下,以整车加权工况平均能量消耗最小为目标,分别采用粒子群算法(particle swarm optimization,PSO)和遗传算法(genetic algorithm,GA)对轮边电机驱动型电动汽车固定挡速比进行优化设计,优化过程软件架构如图2所示。

图2 传动系统速比优化软件架构
3.1 优化目标函数
轮边电机驱动型电动汽车的优化目标是在整车动力性约束条件下,尽可能提高整车经济性,为提高电动汽车对不同循环工况的适用性,在工况加权因子下,确定整车加权工况平均能量消耗最小为优化目标函数,整车加权工况平均能量消耗值为:
(13)
其中,Wcyc为整车加权工况平均能量消耗值;PNEDC-cyc为NEDC工况电池输出功率;TNEDC-cyc为NEDC工况仿真时间,其值为1 200 s;PUDDC-cyc为UDDC工况电池输出功率;TUDDC-cyc为UDDC工况仿真时间,其值为1 367 s;PJC08-cyc为JC08工况电池输出功率;TJC08-cyc为JC08工况仿真时间,其值为1 200 s。
3.2 约束条件及约束处理
固定挡速比优化过程中,主要包括整车动力性约束(最高车速、加速时间和最大爬坡度)以及驱动轮极限附着力的限制。
根据车辆设计行驶最高车速和电机最高转速,确定固定挡速比i上限值为:
(14)
根据车辆稳定车速爬坡时性能需求,确定固定挡速比i下限值为:
(15)
根据0~100 km/h加速时间要求,确定固定挡速比i约束为:
(16)
根据车轮最大驱动力不大于地面对各驱动轮的最大附着力Fxmax,确定固定挡速比i上限值为:
(17)
根据电机最高转速时峰值转矩Tm产生的驱动力不小于最高行驶车速下的行驶阻力,确定固定挡速比i下限值为:
(18)
由(14)~(18)式可得固定挡速比i的取值范围为[6.341,6.778],而速比优化设计过程属于有约束实际工程优化问题,常见的约束优化处理方法主要包括比较个体优劣法、罚函数法以及双适应值法等[10]。本文选用比较个体优劣法作为约束处理方法。
3.3 基于智能算法的速比优化设计
3.3.1PSO算法
基于PSO算法的速比优化设计流程如图3所示,每个可能的固定挡速比解被认为是搜索空间的1个粒子,且每个粒子都有1个与目标函数对应的适应度值,假设在该一维空间中,由n个粒子组成的种群X=(X1,X2,…,Xn),根据目标函数计算出每个粒子位置Xi对应的适应度值,其中第i个粒子的速度可表示为Vi,个体极值为pi,种群的群体极值为pg。在每次迭代的过程中,粒子按照以下规则更新自身的速度和位置[11],即
Vi(t+1)=wVi(t)+c1rand[pi(t)-
(20)
其中,w为惯性权重因子,其值为0.72;c1和c2为学习因子,其值为1.49;rand为取0~1之间的随机函数。仿真中n为30,迭代次数为40。

图3 PSO算法流程
3.3.2GA算法
基于GA算法的速比优化设计流程如图4所示。
(1) 编码成位串。将固定挡速比编码转化为二进制字符串,构成1个串结构数据(即染色体),本文的i变化范围为0.437,为确保优化数值精确到小数点后4位,选择9位二进制编码。
(2) 生成初始种群。1个串结构数据作为种
群中的1个个体,初始随机生成N个串结构数据构成初始种群,仿真过程中N为30。
(3) 计算适应度。通过目标函数与适应度的映射关系得到个体的适应度。
(4) 选择与遗传。选择个体适应度较大的个体作为下一代遗传的基础,通过交叉与变异对个体串结构进行部分修改,防止过早陷入局部收敛。
(5) 重新插入生成新种群。将经过选择、交叉与变异操作后的串结构数据,重新插入并取代原始种群中的串结构数据,形成新的种群。
(6) 终止条件判断。当迭代次数少于或等于设定的迭代次数M时,跳转至步骤(2);反之结束优化过程,仿真过程中M为40。

图4 GA算法流程
3.4 整车动力性仿真平台
本文基于Matlab/Simulink搭建了后向为主、前向为辅的纯电动汽车整车动力学仿真模型,模型如图5所示。
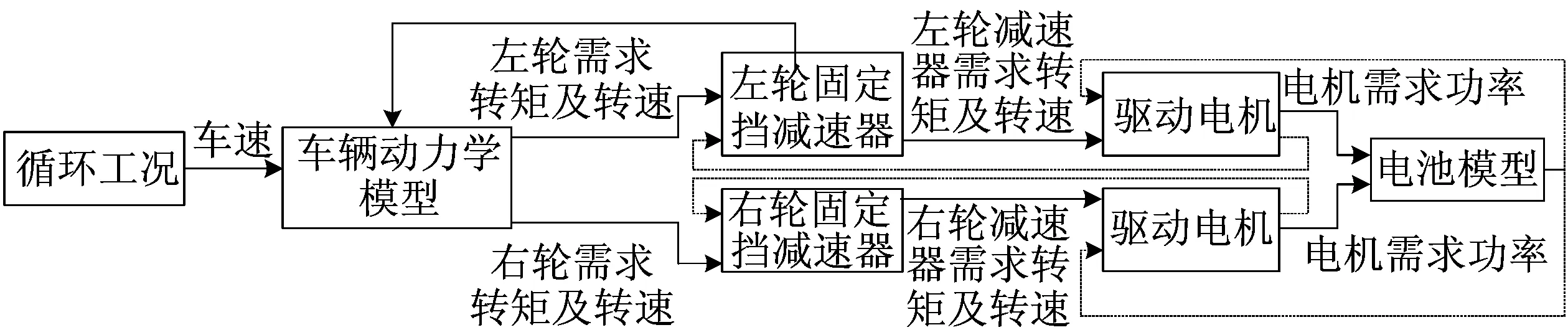
图5 纯电动汽车动力学仿真模型
4 仿真分析
为了验证以加权工况平均能耗最小为目标的速比优化设计方法能够兼顾不同工况下的能耗经济性,本文增加了以单循环NEDC工况能耗最小为目标的速比优化仿真。2种优化目标下不同优化算法的整车性能仿真结果见表3所列。由表3可知,2种优化目标下的整车性能均满足设计性能指标,且以加权工况平均能耗最小为目标优化设计方法下的多项整车性能更优,验证了本文优化设计方法的有效性。
以加权工况平均能耗最小为目标,基于PSO和GA算法的适应度值变化情况如图6所示。以加权工况平均能耗最小为目标,基于PSO和GA算法的固定挡减速器速比优化情况如图7所示。

表3 2种优化目标下速比优化后的整车性能
由图6、图7可知,2种优化算法下的速比寻优结果相同,由于GA中的选择、交叉以及变异算子的使用,与PSO相比,其速比优化过程波动更大。

图6 加权工况平均能耗最小为目标的适应度值变化
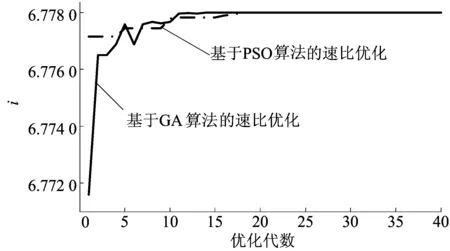
图7 加权工况平均能耗最小为目标的速比优化
以单循环NEDC工况能耗最小为目标,基于2种优化算法下的速比优化情况如图8所示。

图8 单循环NEDC工况能耗最小为目标的速比优化
由图7、图8可以看出,以加权工况平均能耗最小为目标的速比优化值(6.778 0)大于以单循环NEDC工况能耗最小为目标的速比优化值(6.398 4),并且给出了不同优化目标下速比优化值的NEDC和UDDC能耗仿真情况,结果如图9所示。

图9 2种速比下NEDC和UDDC工况能耗仿真
从图9中可以看出,速比为6.778 0下的NEDC和UDDC工况能耗处于速比为6.398 4的2种工况能耗之间,且由表3中2种优化目标下的整车UDDC和NEDC工况能耗值可以看出,尽管以NEDC工况能耗最小为目标的整车能耗比加权工况的低7.83 kJ,但其UDDC工况能耗比加权工况的高16.15 kJ,表明了以单循环NEDC工况能耗最小为目标的优化设计方法只能确保NEDC工况下的能耗最优,而无法顾及其他工况下的能耗情况,因此,进一步验证了以加权工况平均能耗最小为目标的速比设计方案的有效性,其具有更好的工况适用性。
2种优化目标下整车加速性能仿真曲线如图10所示。
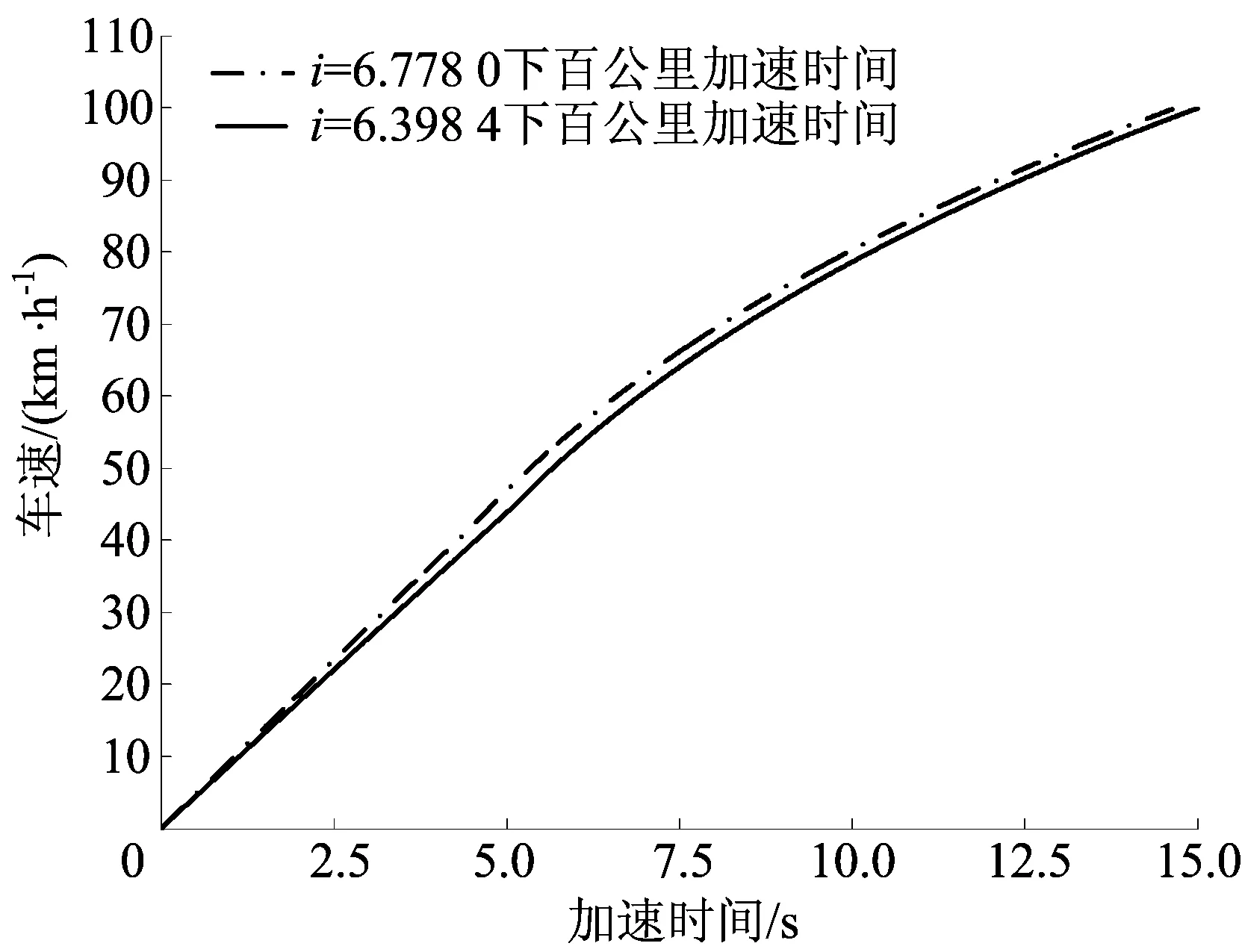
图10 2种速比下加速性能仿真
2种优化目标下的加速时间均小于15 s,满足整车设计性能指标,因为以加权工况平均能耗最小为目标的优化速比值更大,所以比以单循环NEDC工况能耗最小为目标的百公里加速时间提高了0.28 s。
5 结 论
本文针对前轮轮边电机驱动型电动汽车的动力传动系统,给出了以工况加权因子下车速高频区间与电机高效区间相重合为原则和满足整车设计性能指标的轮边电机与蓄电池参数匹配方法;提出了以加权工况平均能耗最小为目标,整车动力性为约束,基于PSO和GA算法的固定挡速比优化设计方法;仿真分析表明整车性能均达标,并通过对比以单循环NEDC工况能耗最小为目标的速比优化结果,表明以加权工况平均能耗最小为目标的优化速比能够兼顾不同工况达到能耗最优,提高了车辆对不同工况的适用性。
[1] 孟庆华,许进,王东峰.轮毂电机驱动型电动汽车动力系统研究[J].农业机械学报,2013,44(8):33-37.
[2] 智晋宁,项昌乐,朱丽君,等.轮边电机驱动汽车性能仿真与控制方法的研究[J].汽车工程,2012,34(5):389-393.
[3] 陈东,徐寅,梁华军.双电机后轮驱动混合动力汽车电子差速控制的研究[J].汽车工程,2013,35(1):46-50.
[4] 张媛媛.采用电动轮驱动的电动汽车转矩协调控制研究[D].长春:吉林大学,2009.
[5] 翟丽,董守全,罗开宇.四轮毂电机独立驱动车辆转向电子差速控制[J].北京理工大学学报,2010,30(8):901-905.
[6] HADDOUN A,BENBOUZID M,DIALLO D,et al.Modeling,analysis,and neural network control of an EV electrical differential[J].IEEE Transactions on Industrial Electronics,2008,55(6):2286-2294.
[7] 周兵,江清华,杨易.两挡变速器纯电动汽车动力性经济性双目标的传动比优化[J].汽车工程,2011,33(9):792-797.
[8] 秦大同,周保华,胡明辉,等.两挡电动汽车动力传动系统的参数设计[J].重庆大学学报,2011,34(1):1-6.
[9] GUZZELLA L,SCIARRETTA A.Vehicle propulsion systems: introduction to modeling and optimization[M].Heidelberg:Springer Verlag,2005.
[10] 龚贤武,唐自强,吴德军,等.两挡纯电动汽车动力传动系统参数设计与仿真[J].郑州大学学报(工学版),2015,36(3):39-43.
[11] 刘华蓥,林玉娥,王淑云.粒子群算法的改进及其在求解约束优化问题中的应用[J].吉林大学学报(理学版),2005,43(4):472-476.
(责任编辑 胡亚敏)
Optimization design of powertrain parameter for in-wheel motor driven electric vehicles
GONG Xianwu1, TANG Ziqiang2, ZHAO Xuan2, XU Shiwei2, HE Yilin2
(1.School of Electronic and Control Engineering, Chang’an University, Xi’an 710064, China; 2.School of Automobile, Chang’an University, Xi’an 710064, China)
The powertrain parameters for electric vehicles driven by in-wheel motor were designed. Firstly, according to the principle which makes the speed range of driving condition and the high efficiency range of the motor coincide, and the performance requirements of vehicle, a weighting factor of driving condition was introduced, and the parameters of the motor and the battery were matched. Then treating the vehicle dynamics indicators as constraint, and treating the minimal average energy consumption of weighting driving condition as target, the fixed gear ratio was designed respectively by particle swarm optimization(PSO) and genetic algorithm(GA). The vehicle performance was simulated and analyzed by the vehicle performance simulation platform which is built on Matlab/Simulink. The simulation results show that the vehicle performance can meet the design requirements; comparing with the result of ratio optimization whose target is the minimal energy consumption of single NEDC condition, it is shown that the gear ratio optimization design method can take into account the energy consumption of different economic conditions, whose target is the minimal average energy consumption of weighting driving condition, and this method has better applicability.
electric vehicle; in-wheel drive; parameter matching; ratio optimization; intelligence algorithm
2015-09-29;
2015-11-30
国家高技术研究发展计划(863计划)资助项目(2012AA111106);国家自然科学基金青年科学基金资助项目(51507013);中央高校基本科研业务费专项资金资助项目(2014G1321040;310822151025);陕西省自然科学基础研究计划资助项目(2016JQ5012)和陕西省工业科技攻关资助项目(2016GY-043)
龚贤武(1978-),男,福建邵武人,博士,长安大学副教授,硕士生导师.
10.3969/j.issn.1003-5060.2017.01.005
U469.72
A
1003-5060(2017)01-0024-07
