某三基发射药贮存寿命的预估方法

顾 妍，张冬梅，张林军，王 琼

(西安近代化学研究所，陕西 西安 710065)

某三基发射药贮存寿命的预估方法

顾 妍，张冬梅，张林军，王 琼

(西安近代化学研究所，陕西 西安 710065)

在95、 90、85、75 和65 °C下对某三基发射药进行热加速老化试验，以老化过程中安定剂的含量变化作为原始数据，采用Berthelot方程及修正的Arrhenius方程对不同温度模式下发射药的贮存寿命进行预估，并将预估结果与自然贮存结果进行对比验证。结果表明，安定剂分解深度为6.6%时，采用Arrhenius方程得到的预估结果准确性较高，而分解深度为50%时，采用Berthelot方程得到的预估结果更为可靠。

发射药；安全贮存寿命；动力学参数； Arrhenius方程；Berthelot方程

引 言

含硝酸酯的火药在贮存过程中会发生缓慢分解，导致其使用性能及贮存性能发生恶化，直接关系到整个武器系统的寿命[1-3]。目前，加速老化法是普遍采用的寿命试验方法，即根据高温试验数据建立合适的老化模型，从而对火药样品的安全贮存寿命进行预测。

Arrhenius方程和Berthelot方程是应用最广泛的老化模型。国内外普遍以不同老化温度条件下，根据老化性能评定参数与温度和时间的关系选取一种合适的性能评定参数(如安定剂含量、力学强度、延伸率、凝胶百分数等)，采用Arrhenius方程进行线性回归，进而求出老化表观活化能，实现不同恒定温度下贮存寿命的预测[4]。理论上，采用Arrhenius方程及其经验公式需要注意样品在实验室加速老化试验中发生的反应与自然环境试验是一致的[5-6]。我国的寿命试验方法已建立了相应的标准，其中应用最为广泛的是GJB 770B-2005火药试验法506.1“预估安全贮存寿命 热加速老化法”，即对火药进行不同温度的加速老化，得到各老化温度下安定剂含量降至50%的时间，然后通过Berthelot方程进行回归，求得方程的实验式，外推求得室温下(30或25℃)的安全贮存寿命[7]；与Arrhenius方程相比，Berthelot方程可简化试验和数据处理过程，不需要获得反应速率常数，无需性能随老化时间变化的规律，只要测出各个老化温度下的临界寿命，就可以外推预估寿命，但是不能获得性能评定参数随老化时间变化的趋势[5]。同时，火炸药在半地下仓库中贮存的温度环境也随季节及昼夜交替有一定程度的波动，而不是绝对的恒温环境，也需要考虑实际贮存温度的波动对安定剂分解的影响。

本研究以某三基发射药为研究对象，对发射药进行加速热老化试验，以老化过程中的安定剂变化作为参量，采用不同的老化模型对该发射药的贮存寿命进行预估，分析了老化模型对寿命预估结果准确程度的影响，为该型号发射药的延寿工作及配方设计提供参考。

1 实 验

1.1 样 品

试验样品为20世纪定型生产的某三基发射药，主要成分由硝化棉、硝化甘油、硝基胍、安定剂等组成，其中安定剂的质量分数为1.51%。

1.2 热加速老化试验

依据GJB770B-2005，506.1“预估安全贮存寿命热加速老化法”[7]，于95、 90、85、75和60 °C条件下对发射药样品进行热加速老化，定期取样，采用溴化容量法[7]定期检测发射药热分解过程中有效安定剂含量的变化。

1.3 自然贮存试验

将检测合格的样品密封在防潮袋中，并置于贮存罐中，在半地下仓库中存贮24年后取出，采用溴化容量法检测贮存24年后有效安定剂含量的变化。

1.4 寿命预估

1.4.1 Arrhenius方程寿命计算方法

Arrhenius基本微分方程表示速率常数(k)与温度(T)的关系，得到化学反应速率的表达式为：

(1)

式中：A为指前因子，s-1；E为反应活化能，J/mol；T为温度，K；R为气体常数；k(T)为老化速率，s-1；α为反应深度；f(α)为动力学机理函数。

为确定f(α)及速率常数k(T)的表达式，采用AKTS-Thermokinetics 软件进行反应动力学计算，该软件收录的动力学机理函数的通式为：

f(α)=(1-α)nαm

(2)

软件通过对原始数据进行分析，以某温度下获得的原始数据α和时间作图，通过拟合获得α与时间的关系，从而计算出指前因子(A)、活化能(E)以及机理函数中指数项m、n的取值。该软件主要解决复杂过程不能直接判断的零级、一级或二级等简单级数反应。为估算机理函数模型f(α)的匹配程度及拟合数据的优良性，该软件以模型筛选中最为通用的AIC (Akaike′s Information Criterion)和BIC (Bayesian Information Criterion)信息准则,对不同机理函数模型进行相关权重的排列[4,8-10]。在计算过程中，也可以根据相应的反应机理直接设置m和n的取值范围，在确定反应级数的条件下计算k(T)的表达式。

以计算得到的Arrhenius方程为基础，通过调用任意温度函数T(t)，进一步计算得到样品中安定剂在任意温度贮存时间tα与安定剂分解深度(α)的关系方程：

(3)

另外，以Arrhenius方程的对数形式外推得到常温下的贮存寿命：

lnk=lnA-Ea/RT

(4)

采用该式，根据不同老化温度条件下的实验数据，得到lnk和1/T的线性关系，从而可进行恒温条件下寿命的计算。

1.4.2 Berthelot方程寿命计算方法

假设τ为有效安定剂消耗一定含量所需的时间(规定50%为安全贮存寿命临界点)，对不同温度(T)下的τ值用线性最小二乘法按Berthelot方程[7]进行线性回归，求出火药在常温条件下的安全贮存寿命：

T=A+Blgτ

(5)

2 结果与讨论

2.1 采用Arrhenius方程预估安全贮存寿命

在95、 90、85、75 和65 °C条件下对三基发射药样品进行热加速老化，老化过程中定期跟踪安定剂含量的变化，5组温度条件下总计采样42个试验数据(表1)。由于原始数据呈明显的线性分布趋势，同时，考虑到火炸药寿命的热加速试验中，三基发射药样品的分解深度一般都不超过1%～2%，因此其分解仍处于分解延滞期内，此时分解速度很小，反应近似于零级反应，因此，设定式(2)参数中m=0，n=0，采用AKTS-Thermokinetics 软件对原始数据进行回归分析。针对安定剂含量变化这一类离散型数据，该软件在回归分析过程中不仅考虑线性拟合相关性，同时兼顾各离散型原始数据经过回归分析后预估结果的合理程度。

回归分析得到Arrhenius方程中速率常数k(T)的表达式为：

(6)

在零级反应情况下，对式(1)移相得到

(7)

机理函数的积分形式为：

(8)

将式(3)代入式(2)：

(9)

根据式(6)得到拟合曲线如图1所示，相关老化试验数据及回归分析后的数据如表1所示。

图1 三基发射药在不同温度条件下安定剂含量变化及依据式(6)得到的拟合曲线Fig.1 Change of stabilizer content in tri-base gun propellant at different temperature and fitting curves obtained by Eq.(6)

由于在零级反应过程中，反应深度(α)与时间(t)关系的积分函数是线性方程，反应机理函数的积分形式为：

g(α)=α=kt

(10)

移相，得

t=α/k

(11)

将式(9)代入式(10)，在指定温度条件下安定剂分解至一定深度的时间为：

(12)

采用式(12)可对三基发射药样品进行不同温度条件下的贮存寿命计算。现有的研究工作[1,11-13]一般以老化过程中安定剂含量变化作为判据对含能材料进行安全贮存寿命预估，主要以常温条件(通常为25℃及30 °C)作为预估贮存温度。

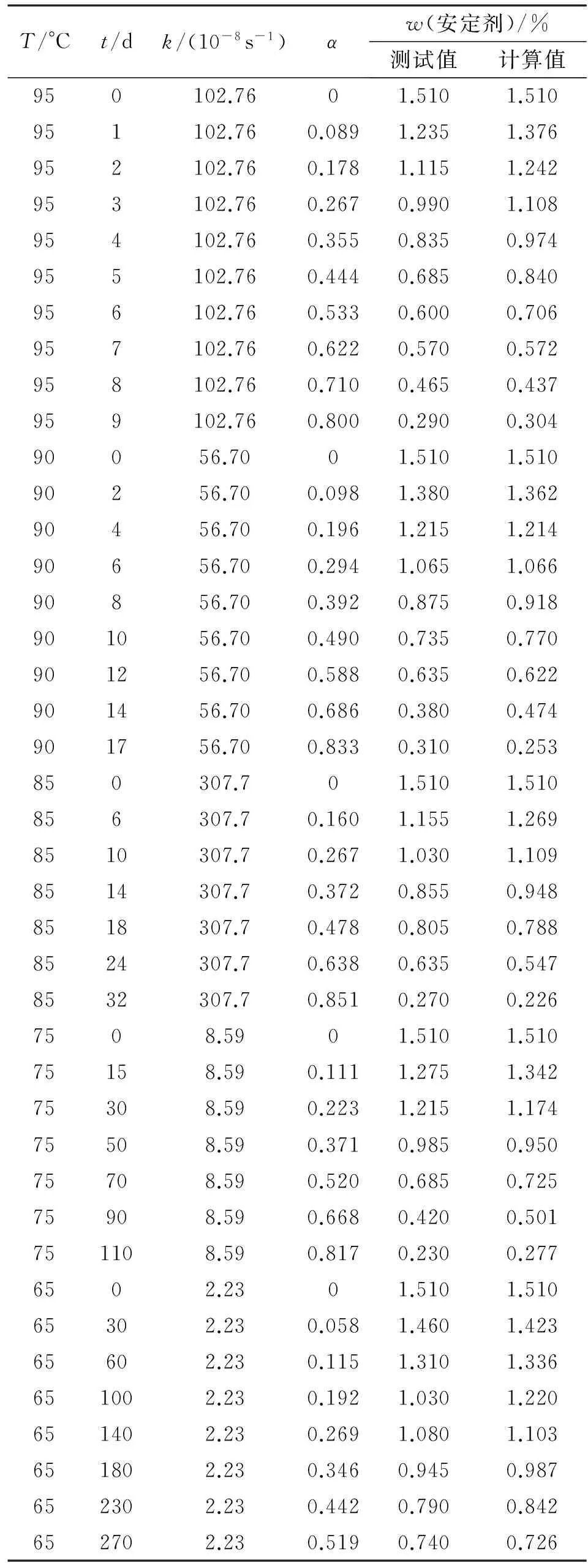
表1 根据老化过程中安定剂分解变化数据计算得到的动力学参数

在置信度为95%的条件下，通过AKTS-Thermokinetics计算得到三基发射药样品在等温条件下安定剂分解深度与贮存时间的变化关系如图2所示，外推安全贮存寿命(α= 50%)如表2所示。

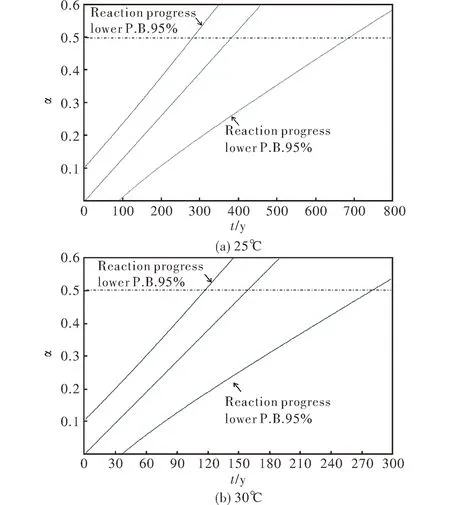
图2 常温条件下安定剂的反应深度与时间的关系Fig.2 Relationships of the reaction depth and time of stabilizer under the normal temperature conditions

T/℃αk(T)/(10-11s-1)τ0.5/y300.59.75663162.5250.54.04753391.7

从表2及图2可以看出， 25 ℃贮存条件下，发射药的安全贮存寿命约为391.7年，若贮存温度提高至30 ℃，发射药样品贮存寿命缩短至162.5年。在置信度为95%的条件下，发射药在25 ℃时贮存寿命为276.7～678.0年，在30 ℃时贮存寿命为117.6～280.8年。

采用Arrhenius方程的对数形式进行安全贮存寿命分析，对老化过程中安定剂含量变化的原始数据作线性拟合，并设定截距为1.51(未老化样品中的安定剂含量)，拟合结果如图3所示。

从图3可看出，有效安定剂消耗一半(α= 50%)时5个温度下的安全贮存寿命分别为5.3、10.1、19.0、66.9和243.2d，相应的反应速率常数(即拟合直线的斜率)为 1.67×10-6、8.68×10-7、4.59×10-7、1.31×10-7和3.59×10-8s-1，应用式(4)进行线性回归，求得Arrhenius对数方程为：

lnk=29.658-15828.399/T

(13)

将式(13)代入式(11)，得到安定剂在某温度下分解至一定深度的时间为：

(14)

根据式(14)外推得到发射药样品在25 °C及30 °C条件下的安全贮存寿命分别为244.1年及101.6年，与通过式(12)获得的预估结果下限较接近。

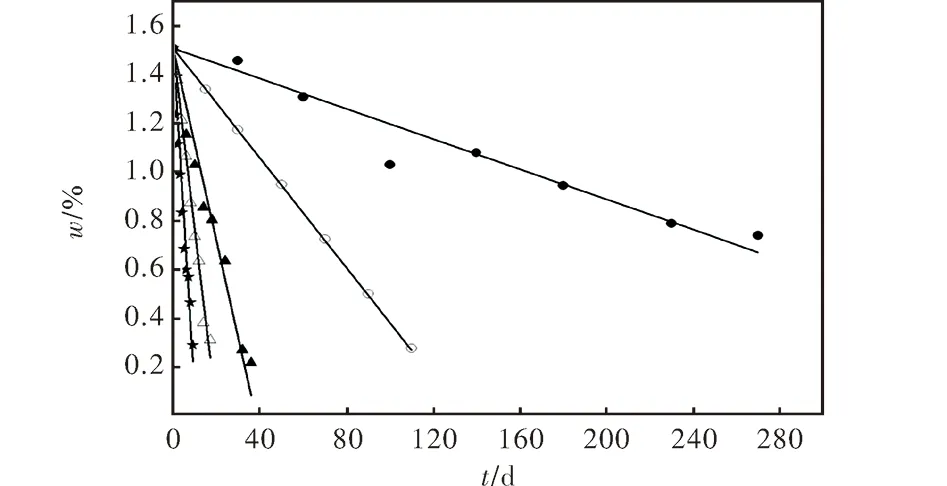
图3 安定剂含量变化的线性拟合曲线Fig.3 The linear fitting curves of change in stabilizer conteat

2.2 采用Berthelot方程预估安全贮存寿命

对老化过程中安定剂含量变化的原始数据作线性拟合，并设定截距为1.51，有效安定剂消耗一半(α= 50%)时5个温度下的安全贮存寿命分别为5.3、10.1、19.0、66.9、和243.2d，应用Berthelot方程进行线性回归，如式(15)所示：

T=470.3-18.1lgτ

(15)

其中R2=1。由式(13)外推求得三基发射药样品在常温25℃及30 °C条件下安全贮存寿命分别为104.8年和55.5年。

2.3 两种寿命预估方法比较及结果验证

采用不同老化模型，其计算结果有一定的差距，因此，应通过一定时间范围内的自然贮存结果对不同算法的寿命预估结果加以验证。三基发射药在半地下仓库贮存24年后，经检测，其中安定剂含量减少至1.4%，计算得到在实际贮存过程中安定剂的分解深度为6.6%。根据图3有效安定剂分解深度为6.6%时，各老化温度点下的贮存寿命分别为0.6、1.2、2.4、8.2、30.2d，应用Berthelot方程进行线性回归，如式(16)所示：

T=454.4-18.1lgτ

(16)

因此，通过Arrhenius方程及Berthelot方程计算常温条件下分解深度为6.6%所需的时间(t)如表3所示。

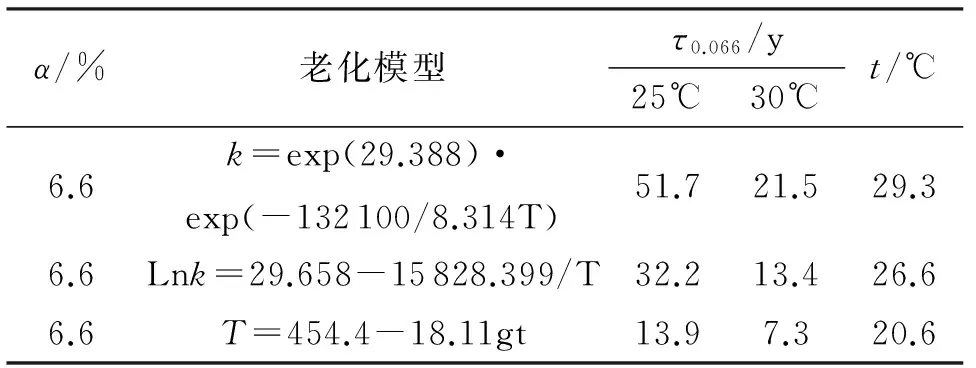
表3 不同老化模型计算常温条件下推进剂的安全贮存寿命

从表3分析得到，采用Arrhenius老化模型计算得到分解深度为6.6%时等效贮存温度均在25～30 °C之间，其中通过式(12)计算得到等效温度为29.3°C，通过式(14)计算得到等效温度为26.6°C；而通过Berthelot方程外推得到的预估寿命明显低于Arrhenius方程的计算结果。结合实际贮存数据，在安定剂分解深度为6.6%时，采用两种Arrhenius老化模型的预估寿命范围均与自然贮存情况比较接近。

实际上，三基发射药在半地下仓库中贮存的温度环境也随季节及昼夜交替，在常温附近有一定的波动，而不是绝对的常温环境。AKTS-Thermokinetics收录了全球各地区的典型温度模型，其中接近于西安全年室内温度变化的模型如图4所示。

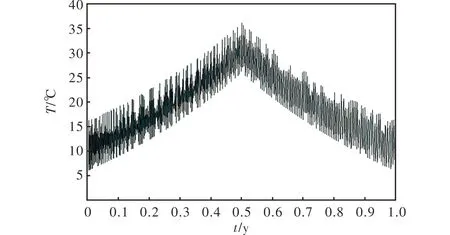
图4 典型全年室内日贮温度变化示意图Fig.4 Schematic diagram of change in the typical indoor diurnal storage temperature throughout the year

该温度模型的平均值约为23°C，且昼夜和四季的交变比较接近三基发射药样品贮存地的实际情况。由于式(12)是通过AKTS-Thermokinetics回归计算获得，因此，在软件中将上述典型温度模型代入该式，计算得到安定剂的分解深度随贮存时间的变化趋势，如图5所示。从图5可以看出，在该温度模式下，安定剂分解深度为6.6%所需的时间约为29年，与自然贮存结果非常接近。这是由于昼夜及四季的温差循环形成了一系列的温度冲击模型，形成交变应力，导致发射药样品中的安定剂含量变化曲线呈现阶梯状的累积损失变化，并且不断增大，结合常温条件下的预估结果，在安定剂消耗程度不高的情况下，采用Arrhenius老化模型预估寿命更接近自然贮存结果。

图5 用式(12)计算得到的安定剂在图4所示温度条件下的反应深度与时间的拟合曲线Fig.5 Fitting curve of the reaction depth and time of stabilizer under the temperature conditions depicted in Fig.4 calculated by Eq(12)

实际上，虽然三基发射药产品的安全贮存寿命是依据安定剂含量变化作为判据，但是在长期贮存过程中，还应当考虑发射药样品可能出现的力学、质量损失、结构完整性等一系列性能变化对贮存可靠性的影响[14]，安定剂含量变化不一定是唯一的失效模式，在多失效模式的情况下，通过安定剂含量评定的安全贮存寿命不完全等同于可靠寿命。而采用Berthelot方程预估的年限更短，可避免依据单一失效模式计算贮存可靠度时，忽视其他模式导致失效的风险。同时，由于Arrhenius老化模型在安定剂少量消耗的情况下预估数据较为准确，在定型产品定期延寿工作中应采用Arrhenius方程与Berthelot方程两种老化模型与自然贮存结果进行综合评定。

3 结 论

(1)当某三基发射药样品中安定剂的分解深度较小(如α= 6.6%)时，使用Arrhenius方程预估老化时间比较接近自然贮存结果，选用的温度函数越接近贮存地的情况，所得到的预估值与真实贮存结果的相关程度越高。

(2)安定剂的分解深度较大(如α= 50%)时预估外推老化寿命，需要考虑三基发射药样品在长期贮存过程中的力学、质量损失、结构完整性等一系列性能变化，由于通过Berthelot方程获得的外推寿命远小于Arrhenius方程的预估结果，结果的可靠度较高，因此在新型号产品研制、评价过程中应使用Berthelot方程预估安全贮存寿命。

(3)在定型产品阶段性延寿工作及剩余寿命预估工作中，应同时采用Arrhenius方程与Berthelot方程两种老化模型与自然贮存结果进行综合评定。

[1] 衡淑云,韩芳,张林军,等.硝酸酯火药安全贮存寿命的预估方法和结果[J].火炸药学报,2006,29(4):71-76.HENG Shu-yun,HAN Fang,ZHANG Lin-jun,et al.Estimation method and results of safe storage life for nitrate ester gun-propellants[J].Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2006,29(4):71-76.

[2] Asthana S N,Deshpande B Y.Evaluation of various stabilizers for stability and increased life of CMDB gun-propellants[J].Propellants,Explosives,Pyrotechnics,1994,19(5):266-269.

[3] Bellarmy A J,Bellerby J M,Sammour M H,Stabilizer reaction in cast double base rocket propellants.Part VII: Effect of lead based ballistic modifiers on the reaction of gun-propellant stabilizer during simulated aging of castdouble base solid propellants[J].Propellants,Explosives,Pyrotechnics,1996,21(2):85-89.

[4] Roduit B,Hartmann M.Prediction of thermal stability of materials by modified kinetic and model selection approaches based on limited amountof experimental points [J].Thermochimica Acta,2014,579:31-39.

[5] 刘子如，邵颖惠，任晓宁，常海.预估火炸药寿命的数学模型及其计算[J].火炸药学报,2016,39(2):1-7.LIU Zi-ru,SHAO Ying-hui,REN Xiao-ning,CHANG Hai.Mathematical models and its calculations for predicting the life of explosives and propellants[J].Chinese Journal of Explosives & Propellants(Huozhayao Xuebao),2016,39(2):1-7.

[6] Brown M E,Maciejewski M,Vyazovkin S,et al.Computational aspects of kinetic analysis.Part A: The ICTAC kinetics project-data,methods and results[J].Thermochimica Acta,2000,355:125-143.

[7] GJ87708-2005火药试验方法[S]．北京：国防科学技术和工业委员会，2005．

[9] Didier Clénet,Patricia Probeck.Advanced kinetic analysis as a tool for formulation developmentand prediction of vaccine stability[J].Journal of Pharmaceutical Sciences,2014,103(10): 3055-3064.

[10] Roduit B,Odlyha M.Prediction of thermal stability of fresh and aged parchment[J].Journal of Thermal Analysis and Calorimetry,2006,85(1): 157-164.

[11] Manfred A,Fred V.Aging behavior of propellants investigated by heat generation,stabilizer consumption,and molar mass degradation[J].Propellants Explosives Pyrotechnic，1992,17:171-178.

[12] Rolf F,Martin N.Stabilizer depletion in single base propellant from unexploded ordnance[J]．Propellants,Explosives,Pyrotechnic，2016,41(4):688-700.

[13] Asthana S N,Divekar C N,Singh H.Studies on thermal stability,autoignition and stabilizer depletion for shelf life of CMDB propellants[J].Propellants,Explosives,Pyrotechnic,1989,21(1):35-46.

[14] 张仕念，易当详，宋亚男，等.固体推进剂多失效模式相关的贮存可靠性评估 [J].含能材料，2007,30(6):525-528.ZHANG Shi-nian，YI Dang-xiang，SONG Ya-nan，et al.Evaluation on storage reliability of solid propellant based on correlative failure modes[J]．Chinese Journal of Energetic Materials，2007,30(6):525-528.

Method of Predicting the Storage Life of a Tri-base Gun Propellant

GU Yan,ZHANG Dong-mei,ZHANG Lin-jun,WANG Qiong

(Xi′an Modern Chemistry Research Institute,Xi′an 710065,China)

The thermal accelerated aging test of a tri-base gun propellant at 95,90,85,75 and 65 °C was performed.Taking the change of stabilizer content in the aging process as the original data,the life of the gun propellant under different temperature mode was estimated and calculated by Berthelot′s equation and modified Arrhenius equation.And the predicted results were compared and verified with the natural storage ones.The results show that when the decomposition depth of stabilizer is 6.6%,the prediction result obtained by Arrhenius equation has higher accuracy,whereas when the decomposition depth of stabilizer is 50%,the prediction result obtained by Berthelot′s equation is more available.

gun propellant; safe storage life; kinetic parameters; Arrhenius equation; Berthelot′s equation

10.14077/j.issn.1007-7812.2017.01.018

2016-08-02；

2016-08-30

总装备部预先研究项目(06101213)

顾妍(1987-)，女，从事火炸药理化性能和老化性能研究。E-mail:guyan0506@126.com

TJ55

A

1007-7812(2017)01-0091-06