基于成年行人头部保护的汽车发动机罩优化*
2017-02-27张良安乔维高
张良安 乔维高
(武汉理工大学汽车工程学院1) 武汉 430070) (现代汽车零部件技术湖北省重点实验室2) 武汉 430070) (汽车零部件技术湖北省协同创新中心3) 武汉 430070) (武汉理工大学华夏学院4) 武汉 430223)
基于成年行人头部保护的汽车发动机罩优化*
张良安1,2,3)乔维高1,2,3,4)
(武汉理工大学汽车工程学院1)武汉 430070) (现代汽车零部件技术湖北省重点实验室2)武汉 430070) (汽车零部件技术湖北省协同创新中心3)武汉 430070) (武汉理工大学华夏学院4)武汉 430223)
通过正交试验的方法优化发动机罩结构,以减小成年行人头部在车-行人碰撞中的伤害.基于Hyper Works和LS-DYNA建立了成人头型冲击器与发动机罩的碰撞有限元模型,仿真结果与数值计算结果相符.借助该有限元模型,研究了影响头部伤害的主要因素的联合作用,包括发动机罩的强度、倾斜角度、厚度和刚度,并通过正交试验挑选出了最优水平组合.与初始模型相比,最优水平组合的头部伤害指标(HIC)降低了19.44%.且HIC对发动机罩的强度、倾斜角度、厚度和刚度的灵敏性依次增加.同时,指出在发动机罩倾斜角度为5°附近做细化研究可进一步提高行人的安全性.
行人头部保护;发动机罩;碰撞;正交试验;头部伤害指标
0 引 言
据统计,2007年中国行人交通事故占交通事故的54.4%[1-2].行人是交通事故中的弱者,其死亡人数占交通事故死亡人数的24.6%[3].经事故分析,行人致死原因62%与头部伤害有关,而头部伤害的20%又与发动机罩有关[4].
乔维高等[5]对影响行人头部伤害的因素进行了深入研究,但并未对这些因素进行方便有效地组合研究.文中运用正交试验的方法研究发动机罩强度、刚度、厚度和倾斜角度对行人头部加速度的影响灵敏度,得出并验证最优水平组合.
1 成人头型冲击器有限元模型
头型冲击器分为成人和儿童头型冲击器.在此,以成人头型冲击器为代表.
1.1 成人头型冲击器模型的建立
文献[1]对成人头型冲击器的几何尺寸要求见图1a),且应满足质量m=(4.5±0.1) kg、质心与几何中心偏差在5 mm以内,对过质心且垂直于冲击方向的轴的转动惯量I=0.010~0.013 kg·m2等静力学条件.
按照图1a)的要求,可以把模型简化成底板,球体和头皮3部分,见图1b),几何参数上设定3个调节参数,建立其质量方程,质心方程和转动惯量方程,使之满足静力学要求,进而可求出设定的3个参数[6].按照设定的几何尺寸和形状,可在CATIA中建立初始模型,见图2.
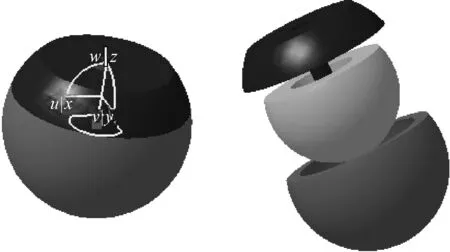
图2 成人头型冲击器CAD模型
有限元模型在Hyper Mesh中建立.相对于球体和底板,头型的外层头皮较易变形,在碰撞过程中易出现负体积而无法运算,故要求网格较细.同时,在头皮外表面覆盖一层空壳单元.为了提高计算精度,球体、底板和头皮两两之间共节点连接,外层空壳单元从头皮三维网格上提取、与头皮共节点连接,自动面面接触.网格划分为5 mm的四面体网格,共有26 910个节点,135 127个单元.
根据材料特性,LS-DYNA中的6号粘弹性材料可以很好地模拟头皮材料,而球体和底板采用MAT20刚性材料模拟较好.通过建立基于响应面法的参数优化模型,即可得到满足频率和加速度等条件的最佳材料参数.最终确定的材料参数见表1,有限元模型见图3.最终头型冲击器的静力学参数为:m=4.483 kg,质心坐标(0,0,0),Ix=Iy=0.011 5 kg·m2,符合法规要求.

表1 成人头型冲击器材料参数
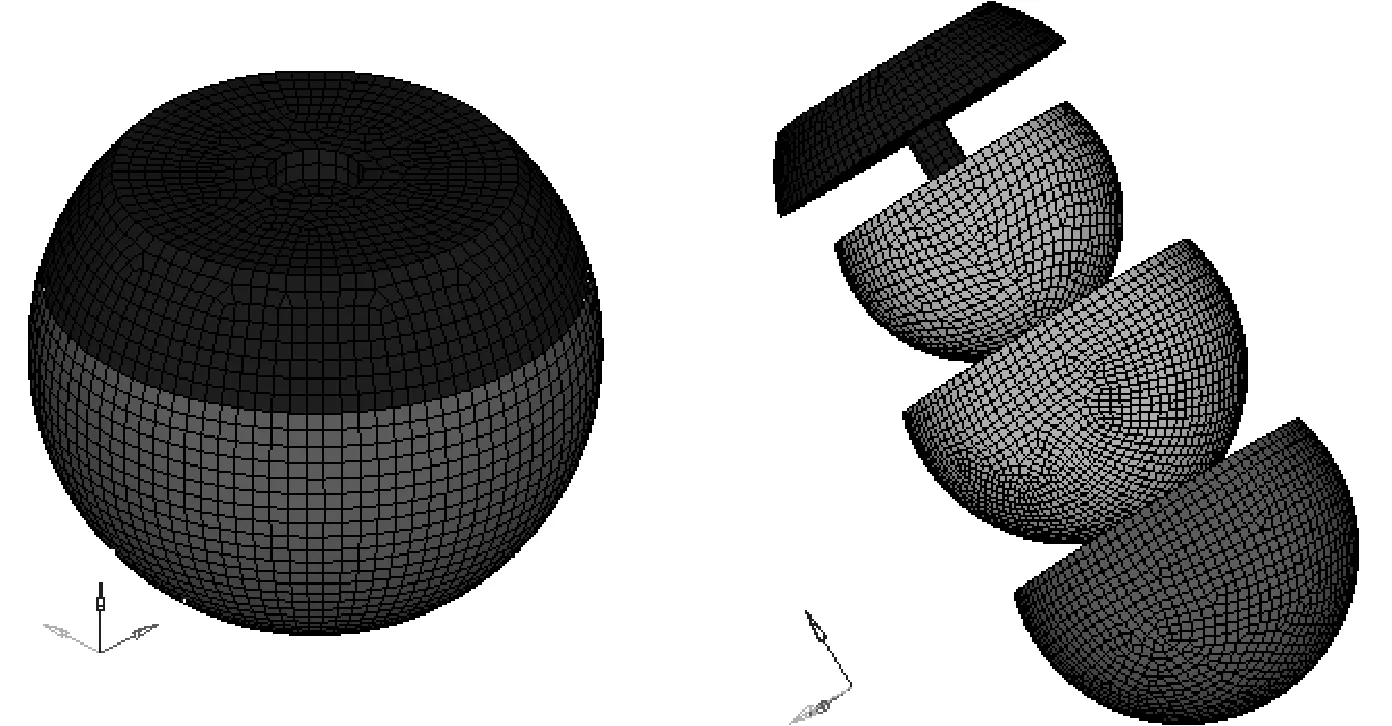
图3 成人头型冲击器CAE模型
1.2 成人头型冲击器的标定
动力学上,成人头型冲击器需进行标定试验,试验方法见图4a).跌落高度为(376±1) mm,跌落角度为65°±2°,刚板尺寸大于300 mm×300 mm×50 mm.要求其下落过程不旋转,且满足峰值加速度在225~275g之间.
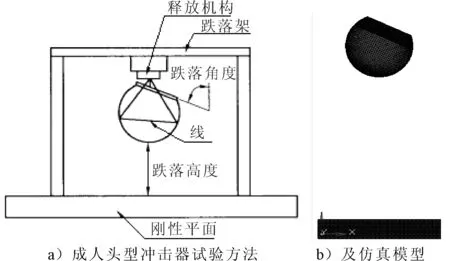
图4 成人头型冲击器
按照上述试验条件,对头型进行仿真标定,其模型见图4b).经过计算和后处理,标定试验所得头型质心加速度时间历程见图5.易知峰值加速度amax=264g,符合法规要求,可用于以下研究.
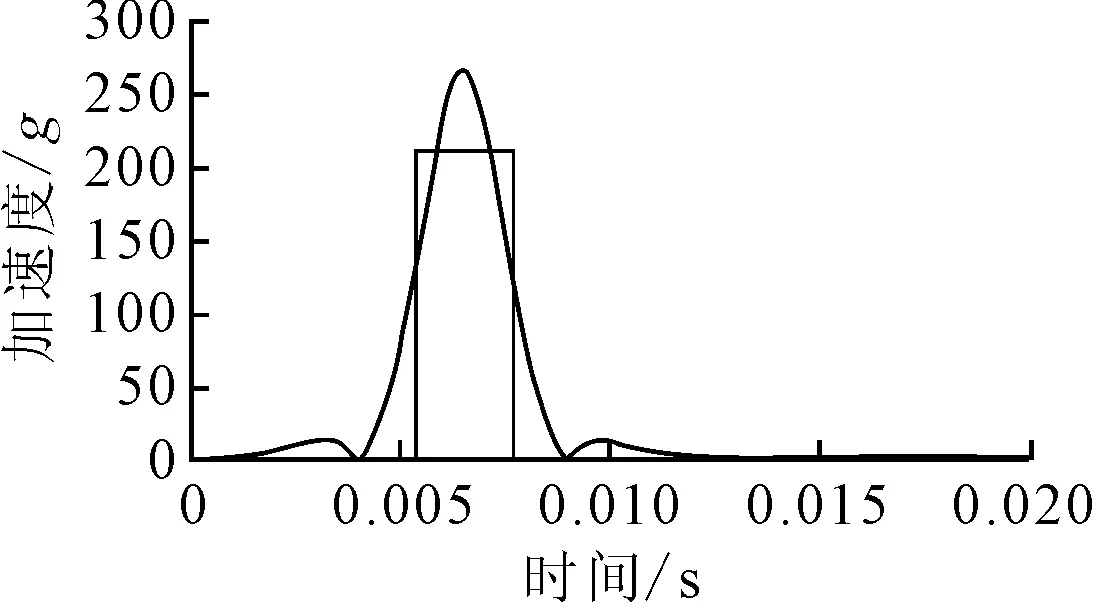
图5 标定模型质心加速度时间历程
2 发动机罩碰撞仿真及分析
根据某车型发动机罩几何和材料参数,建立其简化模型,见图6.根据球体与薄板冲击的力学原理,可得到头型与发动机罩碰撞的微分方程
(1)
(2)
式中:m1,m2为头型和发动机罩的质量;x1为头型的位移;x2为发动机罩的变形位移;kb为发动机罩的等效弯曲刚度;km为发动机罩的等效薄膜刚度;h(x1~x2)为碰撞模型的力-位移函数.
联立式(1)和式(2),可对头型与发动机罩碰撞过程的动力学响应进行计算,得到的头型质心峰值加速度约为171g.
头型冲击器以9.7±0.2 m/s的速度撞击发动机罩,碰撞点位于中心线上离发动机罩前缘1.0 m处,冲击方向与水平面呈65°±2°的夹角.碰撞过程中头型与发动机罩自动面面接触.
经过LS-DYNA求解计算得到的质心加速度时间历程曲线见图6,整体上曲线呈现出一个峰值,峰值加速度约为163g.与计算模型的误差在5%以内,该模型可用于后续分析和仿真.曲线的单峰主要是头型直接与发动机罩外板碰撞产生的较大反作用力而形成的.波峰加速度与外板厚度、外板材料和接触部件数等有关[7].
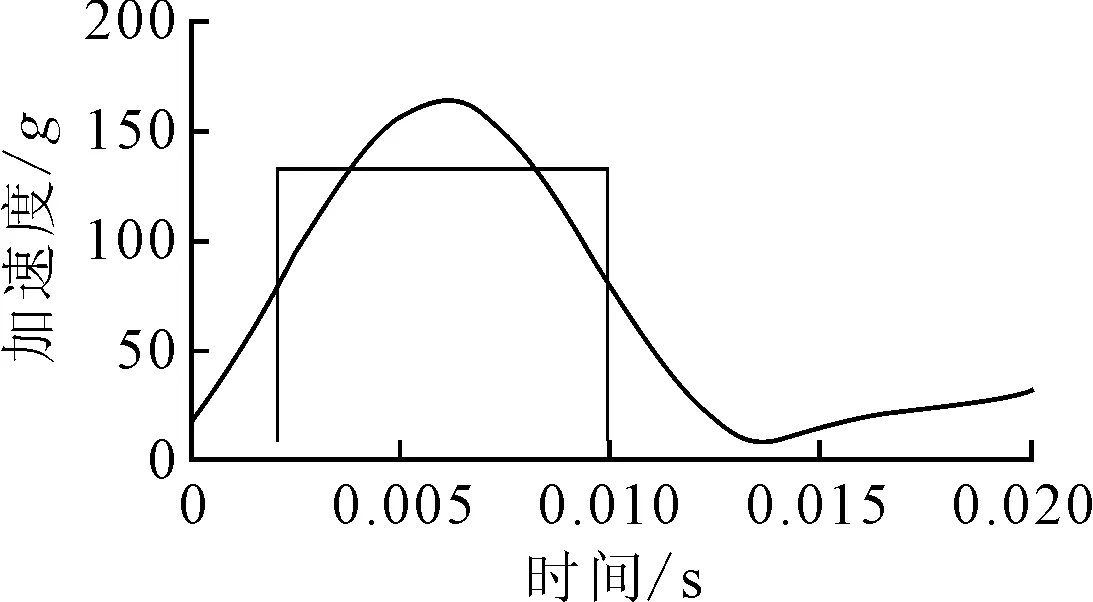
图6 初始模型质心加速度时间历程
HIC为头部伤害程度的重要评价指标,其值越小表示头部伤害程度越小,对行人的保护越有利.按式(3)计算.
(3)
式中:t1,t2为碰撞中的2个时刻,t2-t1≤15 ms;a为头型质心加速度时间历程,g.
经过滤波和计算,得到该模型的HIC=1 368,远大于法规规定的1 000.本人在前续研究中,已经探讨了发动机罩外板厚度、屈服强度、长度、和曲率半径对HIC值的影响[8-9].故文中运用正交试验的方法对发动机罩强度、刚度、厚度和倾斜角度进行优化设计.
3 正交试验优化方案
3.1 正交试验
由材料力学知,可用材料的屈服强度和罩板的长度分别表示发动机罩的强度和刚度.根据该车型实际情况,分别选取其屈服强度、长度、厚度和倾斜角度上的3个水平,见表2.
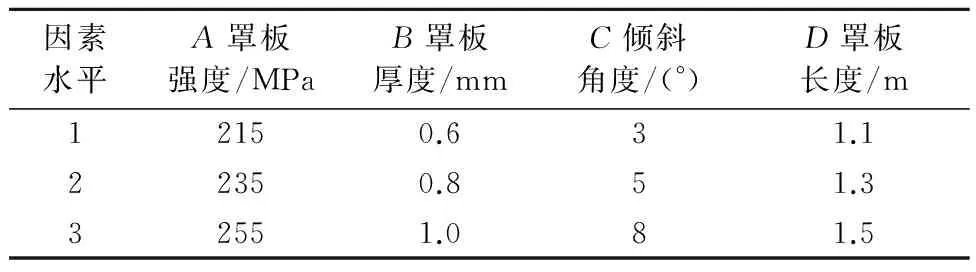
表2 因素水平表
该问题为4因素3水平,采用L9(34)正交试验表,只需做9次仿真试验即可得出最佳水平组合,见表3.
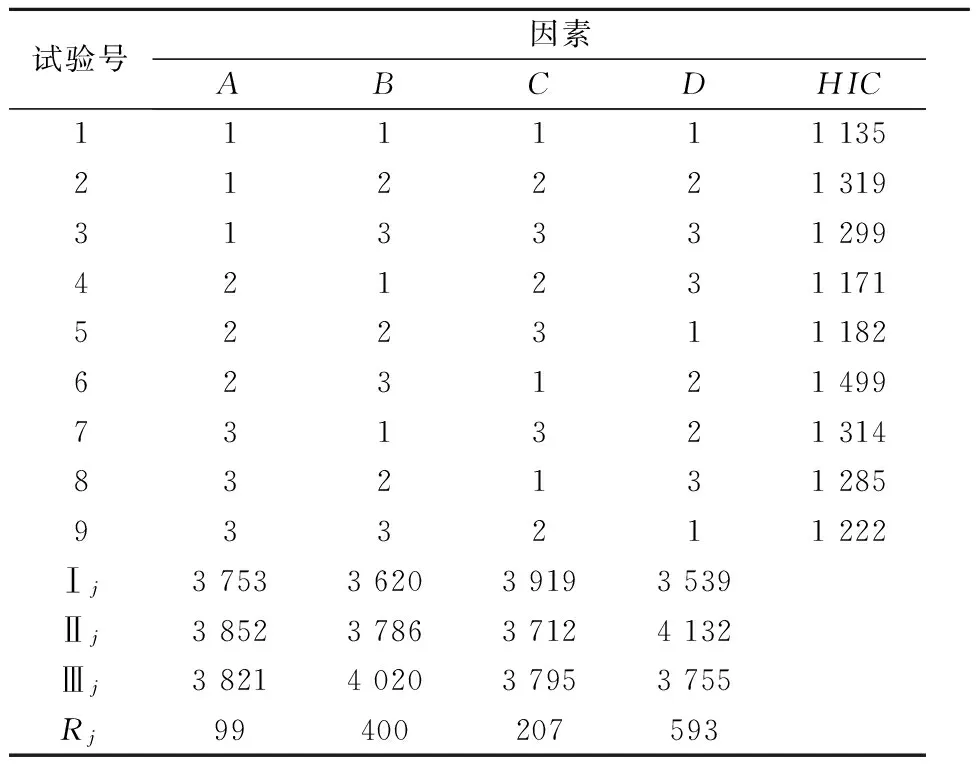
表3 L9(34)正交试验表及统计结果
3.2 正交试验结果分析
按表3依次进行仿真试验,并记录试验结果于表3中.其中,Ⅰj,Ⅱj,Ⅲj为第j个因素的1,2,3水平的HIC总和;Rj为第j个因素的水平极差.
最优水平组合分析及验证:每个因素的每个水平均与其他因素水平进行了一次试验,故Ⅰj,Ⅱj,Ⅲj可分别代表该因素的3个水平的优化作用大小.其中:Ⅰj,Ⅱj,Ⅲj越小,该水平越优.易知,该组试验的最优水平组合为A1B1C2D1.
按照A1B1C2D1水平进行验证试验,其仿真结果见图7,其峰值加速度约为160g,HIC=1 102.相对于初始模型,HIC减小了19.44%.
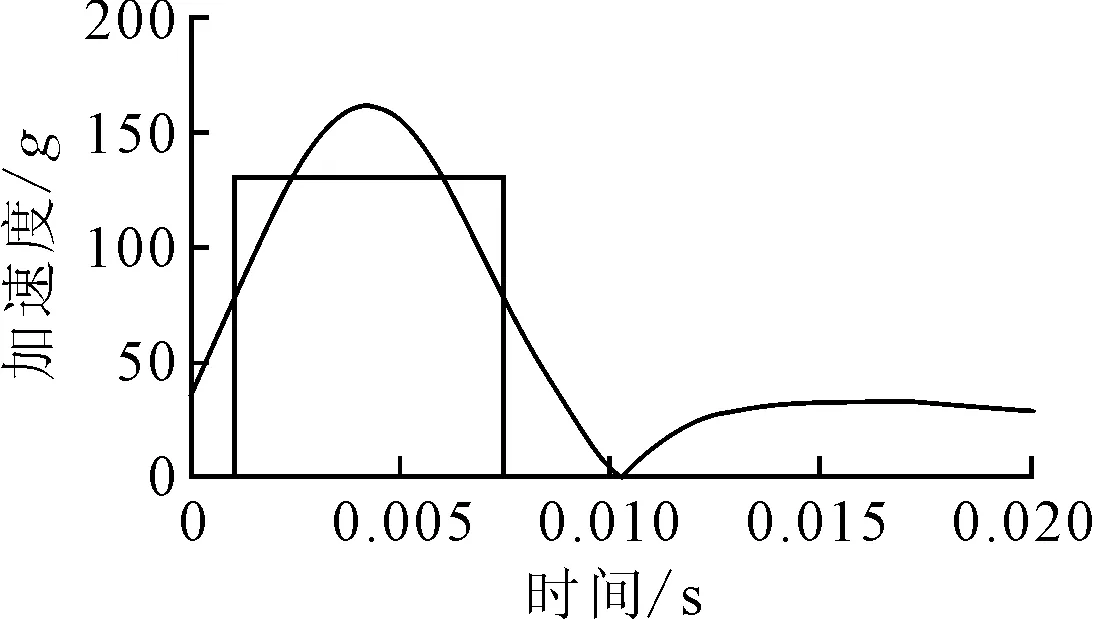
图7 优化模型质心加速度时间历程
灵敏度分析:某因素的水平变动造成试验结果变化越大,有理由认为头部伤害指标对该因素越灵敏.由表3可知,RA 进一步的细化研究分析:由表3可知,可对各因素水平下的HIC值做如下统计,观察其变化趋势,其结果见图9.对于罩板倾斜角度在5°附近做更细化的研究,适当降低强度,厚度和长度可能得到更优结果. 图8 各因素水平的HIC变化趋势 1) 正交试验得到的最优水平组合为A1B1C2D1.其仿真试验得到的HIC约为1 102,相对于原模型,降低了19.44%. 2) 罩板强度、刚度、厚度和倾斜角度4个因素中,HIC对其灵敏度从小到大依次为:强度<倾斜角度<厚度<刚度. 3) 为了得到更优化的结果,可以对罩板倾斜角度在5°附近做更细化的研究. [1]中国汽车技术研究中心.汽车对行人的碰撞保护:GB/T 24550—2009[S].北京:中国标准出版社,2010. [2]张铁川,朱西产,苗强,等.针对行人保护头部碰撞的发动机罩设计方法[J].汽车技术,2009(12):24-28. [3]胡昌东,董俊红,于波.基于成年行人头部保护的发动机罩仿真分析[J].农业装备与车辆工程,2014,52(6):46-50. [4]宋新端,兰凤崇,李新贤,等.弹起式发动机罩的行人保护性能研究[J].机械设计与制造,2013(12):97-100. [5]乔维高,朱西产.行人与汽车碰撞中头部伤害与保护的研究[J].农业机械学报,2006,37(9):29-31. [6]叶辉,胡平,胡兴军.行人保护头型冲击器有限元建模方法研究[J].汽车技术,2011(6):1-6. [7]HUANG S N, YANG J K. Optimization of a reversible hood for protecting a pedestrian’s head during car collisions[J].Accident Analysis and Prevention,2010(42):1136-1143. [8]葛如海,邱奇峰,应龙,等.基于LS-DYNA的行人头部保护发动机罩优化[J].广西大学学报(自然科学版),2014,39(3):598-606. [9]彭勇,陈勇,杨济匡.基于儿童行人头部保护的发动机罩设计分析[J].江苏大学学报(自然科学版),2013,34(5):502-507. Optimization of Vehicle Engine Hood Based on Protecting Adult-pedestrian Head ZHANG Liang’an1,2,3)QIAO Weigao1,2,3,4) (SchoolofAutomotiveEngineering,WuhanUniversityofTechnology,Wuhan430070,China)1)(HubeiKeyLaboratoryofAdvancedTechnologyofAutomotiveComponents,Wuhan430070,China)2)(HubeiCollaborativeInnovationCenterforAutomotiveComponentsTechnology,Wuhan430070,China)3)(WuhanUniversityofTechnologyHuaxiaCollege,Wuhan430223,China)4) In order to reduce adult-pedestrian head injury during vehicle-pedestrian collision, the paper aims to optimize the structure of engine hood by orthogonal experiment. In the paper, a FEM model of an adult-head form impactor colliding with an engine hood is built based on Hyper Works and LS-DYNA and its results are consistent with numerical results. Based on the FEM model, the combining effect for head injury of many main factors including the strength, tilt angle, thickness and stiffness of hood has been studied and the optimal combining level has been selected by arranging orthogonal experiment. Compared with the original model, the head injury criterion (HIC) of the optimal structure reduces 19.44% and the sensitivity ofHICis gradually increasing in the strength, tilt angle, thickness and stiffness of hood. Meanwhile, the article points out that refinement study on tilt angle of hood around 5°can further improve the pedestrian’s safety to. pedestrian head protection; engine hood; collision; orthogonal experiment;HIC 2016-10-31 *汽车零部件技术湖北省协同创新中心专项项目资助(20132r0001) U461.91 10.3963/j.issn.2095-3844.2017.01.030 张良安(1992—):男,硕士生,主要研究领域为汽车被动安全、汽车CAD/CAE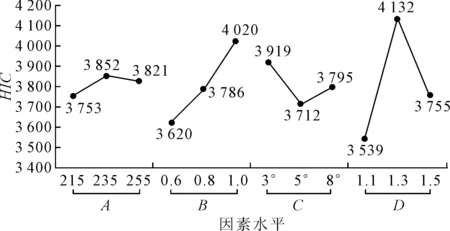
4 结 论
