基于正弦光栅相位调制的三维测量

吴泓欣，王拥军

（1. 中国人民大学附属中学，北京市 100080；2. 北京邮电大学，北京市 100876）

基于正弦光栅相位调制的三维测量

吴泓欣1，王拥军2

（1. 中国人民大学附属中学，北京市 100080；2. 北京邮电大学，北京市 100876）

高分辨率三维轮廓的测量在现代社会有着广泛应用，本文对正弦光栅相位调制的三维测量方法进行了理论研究，用计算机控制数字投影设备产生正弦条纹光栅，利用CCD采样分步移相的图案，通过解包裹的方法获得物体的三维信息，测量精度达到10微米。

光学工程；三维测量；正弦光栅；分步移相

0 引言

随着工业自动化不断发展，三维增材制造技术的日益成熟以及逆向工程的逐步应用，对复杂物件的高分辨率三维轮廓的实时测量的研究提出了要求。结合高端设备制造，高分辨率三维轮廓测量在国防军事、航空航天、机械制造、模具设计、医学整形、文物保护、安全、美容、娱乐等诸多领域都有重要应用。例如在航空机械制造中，发动机叶片型面复杂，尺寸跨度大，需要极高的加工精度才能满足飞行器的动力要求。并且发动机叶片工作在高压、高温及高速状态下，容易造成叶片的叶尖、叶面等部位的损伤。因此，航空发动机需要定期进行大修。发动机叶片的加工与大修都需要对其形面的三维尺寸进行精密的测量。又如在文物的保护与修复中，利用高精度三维测量技术，不仅可以对文物进行复原、复制，又可以保存电子数据，为虚拟现实等技术提供精确材料。此外，在虚拟现实技术中，三维轮廓测量可用于场景创建，在虚拟环境中调用测量信息，还原现实物体。

目前，对复杂形面的三维测量方法的主要有三坐标测量法、光学投影测量法[1,2]、电感测量法、标准样板法、激光扫描测距法[3,4]等。三坐标测量法利用三维坐标测量仪器上的机械探针，对被测表面进行逐点测量，测量效率低，探针造价高，损耗大；电感测量法是使用电感量仪测量物体上的典型点上的电感量，需要标准参考件进行比较，测量精度较高，但有效率低、成本高、信息量小等缺点；标准样板法选取一个与理论设计相近的物件作为标准件，在标准件上选取特征点提取特征参数，与被测物件的参数进行比较。该方法测量速度较快，但受主观性影响大，只能用于定性测量。激光扫描测距法使用激光对物件进行逐点扫描，经物体表面反射，测定发射脉冲与反射脉冲的时间差，或通过干涉法得到反射光与参考光的相位差，再将获取的物件表面高度信息与标准件进行比较。该使用脉冲时间差的方法测量精度在亚毫米级，使用干涉法的测量精度在微米级，但需要处理的信息量大，速度慢，对信号处理设备的时间分辨率要求极高[5,6]。

光学投影测量法通过将正弦或编码的光学条纹投到被测物体，利用物体的高度对光学条纹进行调制，通过特定的算法获得被测物体的高度信息。该测量方法具有测量精度高、速度快、操作简单、信息全的特点，并且是一种非接触式测量方法，适合于对复杂形面的高精度测量。

本文利用计算机控制数字投影设备产生正弦条纹光栅，利用CCD采样分步移相的图像，通过解包裹的方法获得物体的三维信息，测量精度达到0.01毫米。该方法使用全数字设备，易于实现工业自动化[7]。

1 测量原理

当两束平行的相干光垂直透射到一个均匀的平面时，平面上的干涉条纹平行而均匀；而当相平面不均匀时，干涉条纹会发生扭曲，这就意味着平面的高度对干涉条纹进行了调制。如果在一个物体上投射了包含相位信息的光学条纹，条纹中的相位信息就会被物体的高度所调制，我们可以通过解相位包裹获得物体的真实高度。

图1 测量系统Fig.1 measuring system

测量系统如图1所示，被测物体放置在参考平面上，在参考平面上建立xoy平面直角坐标系，CCD相机的光心为Oc点，投影仪的光心为Or点，P(x,y)为被测物体上任一点。假设从投影仪发出的一条光线OrB，应投射在参考面上的B点，由于被测物体的存在，该光线投射在物体的P点。从CCD相机的角度看，当没有被测物体时，参考面上的点A成像在CCD阵面上的一点(m,n)，而A点携带的是投影仪发出的OrA光线的信息。由于被测物体的存在，物体上的P点被成像到CCD的(m,n)点，而P点携带的是光线OrB的信息。也就是说，由于物体的存在，CCD上(m,n)点的信息从参考面上的A点变到B点。A点到B点距离AB携带了物体在P(x,y)点的高度h(x,y)的信息。设AB的距离为s，由ΔOrPOc相似于ΔAPB，可以得到：

假设投影的是正弦光栅，在参考面上正弦光栅的空间周期为λ0，参考面上A点与B点的光强可以表示为：

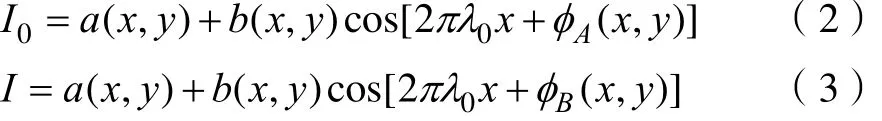
AB之间的距离s为:

由于CCD阵面上(m,n)点在没有被测物体时包含的相位为A点的相位有被测物体时包含的相位为B点的相位于是可以通过两次成像获得A点与B点的相位差。P点的高度为：

其中，i表示移相次数，I0(m,n)为背景灰度，γ(m,n)为调制深度，φ(m,n)为所求相位，iα为第i次移动的相位值。可以得到：

通过对参考面与被测物体进行四次移相，可以获得A与B点的相位，由公式（5）求得被测物体的高度分布。由（8）得到的相位主值φ在一个相位周期内是唯一的，但是由于在整个测量空间内有多个光栅条纹，φ呈锯齿状分布，必须对空间点的相位主值进行相位展开得到连续的绝对相位值φ，这个过程称为解包裹。为了避免解包裹过程中在物体高度梯度较大时的判断错误，一般使用双频外差法。双频外差是指将两种不同空间频率的相位函数φ1和φ2叠加得到一种频率更低相位函数φ。使用外差可法可以对空间点的相对相位在全场范围内无歧义的进行相位展开。

2 实验与讨论

实验系统的配置如图1所示，由DLP数字投影仪，CCD工业相机，参考白屏与被测物体（面具）构成，数据处理在后台由计算机完成。投影仪距参考白屏的距离为80厘米，采用双频外差法，由计算机生成128与127个条纹周期的正弦灰度分布的光栅条纹，通过四步相移分别投到参考白屏及测量面具上。在使用DLP投影仪进行光栅投影时，实际投影出的光栅并不满足标准的正弦分布，给测量带来很大的误差。即使投影仪投影出正弦光栅，CCD采集后很可能也不满足正弦分布。因此，需要对投影采集系统的各种参数进行调整校正。一般先选择投影仪的亮度为50%，对比度50%，通过提取灰度曲线的方法对采集到的条纹的正弦性进行分析。当曲线上宽下窄，且顶部接近CCD的量化的最高值（8位，255），适当降低亮度与对比度；当曲线下宽上窄，且顶部接近CCD的量化的最低值（0），适当提高亮度与对比度。当对比度变小时，造成量化的范围变窄，影响测量精度。当波谷处太小时，CCD采样的噪声较大，一般需要保证波谷处的量化值在40附近。调整投影仪的对比度与亮度，使量化的区间保持在40~240之间。由于正弦光栅由计算机生产，通过调节其背景光与调整度也可以较好的投影效果。结合调节CCD相机到合适的光圈值与曝光时间，可以获得最佳的正弦效果。经过参数校正后得到的参考面与被测面具的条纹图（从16幅图中选两幅）示于图2.

采集到的原始图像包含有噪声和畸变，直接用于运算会带来相位的跳变，造成解包裹的相位不连续，因此必须对图像进行预处理。首先对原始图像进行快速傅里叶变换，得到图像的二维频谱，由频谱选取合适的滤波区间，使用其滤波区间对16幅图进行滤波处理，然后按照公式（8）进行相位φ主值计算，按照双频外差法对折叠相位进行展开。图3给出了被测面具解包裹后不同三维轮廓图，图4给出了与图3对应的面具二维图像，而图5则给出了。可以看出，经过解包裹后的获得的数据包含了真实面具三维轮廓的详细数据。

图2 投影的参考面与面具条纹Fig.2 stripes in reference surface and measured object

图3 面具三维轮廓的不同方向的显示Fig.3 three-dimension contour in different directions

图4 实际面具不同方向的二维图Fig.4 the object in different direction

图5 面具三维轮廓信息中不同截面的曲线Fig.5 curves of different cross-sections

在被测物体的边缘或高度的跳变处，容易出现解包裹错误，表现为其相位点与周边邻域内点的相位值不连续并且不是正常的跳变。在解包裹过程中必须找出这些错误点，并进行纠正。在相位图中，质量值[8]为某点的相位值相对于周边相位的变化量，可以用来表示相位点出错的概率，而质量值可以求梯度的方法得到。图6，7分别为纠错后参考面的连续相位与相位主值的波动，表示相位误差，也可以衡量测量精度。对图7中的主值误差进行统计，可得到Δφ的方差为0.005，相位图的最高点与最低点的相位差为35.7，可以得到相位测量精度为0.014%，对应的高度方向的测量精度为10微米。

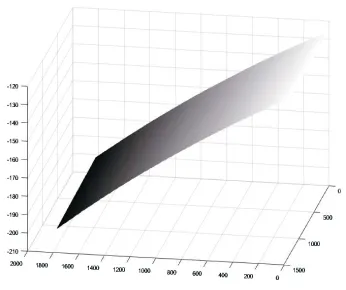
图6 参考平面的相位展开Fig.6 phase unwrapping

图7 参考平面的主值相位波动Fig.7 main phase fluctuates

3 结论

本文针对三维轮廓测量的正弦光栅相位调制的测量方法进行了理论与实验研究，结果表明，当投射的光栅条纹保持良好的正弦性时，通过选取合适的滤波区间可以获得良好的测量效果，测量精度可以达到10微米。

[1] Zhang Z H, Ma H Y, Guo T, et al. Simple and flexible calibration of phase calculation based 3D imaging system. Optics Letters, 2011, 36(7): 1257-1259.

[2] Ma S, Quan C, Zhu R, et al. A fast and accurate gamma correction based on Fourier spectrum analysis for digital fringe projection profilometry. Opt. Commun, 2012, 288(5): 533-538.

[3] Time-of-flight measurement in self-triggering pulsed laser ranging. Optical Engineering, 2005, 44(3): 34201-34205.

[4] A laser time-of-flight range scanner for robotic vision. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1983, 5(5): 505-512.

[5] 王学宁, 韦群. 三维重建效果评价技术综述[J]. 软件, 2016, 37(8): 129-132. WANG X N, WEI Q, Overview on Evaluation of 3D Reconstrction[J]. computer engineering & Software, 2016, 37(8): 129-132

[6] 石照耀, 韦志会. 精密测头技术的演变与发展趋势. 工具技术, 2007, 41(2): 3-8. SHI Z Y, WEI Z H. Evolution and Some Trends in Precision Probe Technology. Tool Engineering, 2007, 41(2): 3-8.

[7] 刘尚武, 魏巍, 矫宇鹏. 三维模型的规格化表示与存储方法研究[J]. 软件, 2016, 37(4): 29-31 LIU S W, WEI W, JIAO Y P. The Normalizing Representation and Storage of 3D Model[J]. computer engineering & Software, 2016, 37(4): 29-31.

[8] Zhang S, Li X L, Yau S T. Multilevel quality-guided phase unwrapping algorithm for real time three-dimensional shape reconstruction. Applied Optics, 2007, 46(1): 50-57.

Three-dimension Measurement Based on Phase Modulation of Sinusoidal Grating

WU Hong-xin1, WANG Yong-jun2
(1. The High School Affiliated to Renmin University of China, Beijing 100080, China; 2. Beijing University of Post and Telecommunications, Beijing 100876, China)

The measurement of high-resolution three-dimension contours has been widely used. In this paper, three-dimension measurement method of phase modulation of sinusoidal grating is studied theoretically. The digital projection equipment is used to generate sinusoidal grating. CCD is applied to sample pictures generated by stepwise phase shift method. Three-dimension information of the object is obtained by the method of unwrapping, and the measuring accuracy is up to 10 microns.

Optical engineering; Three-dimension measurement; Sinusoidal grating; Stepwise phase shift method

TP391.41

A

10.3969/j.issn.1003-6970.2017.01.023

吴泓欣，女，E-mail：1580705036@qq.com；王拥军(1968-)，男，博士，副教授，主要从事光纤通信与光传感等方面的研究。

本文著录格式：吴泓欣，王拥军. 基于正弦光栅相位调制的三维测量[J]. 软件，2017，38（1）：108-114