一种基于表面等离激元的纳米温度传感器

宗 妍，郎佩琳

(北京邮电大学理学院，北京 100876)

一种基于表面等离激元的纳米温度传感器

宗 妍，郎佩琳

(北京邮电大学理学院，北京 100876)

本文基于表面等离激元（Surface Plasmon Polariton，缩写为SPP）共振腔提出了一种新型纳米温度传感器。随着温度的升高，金属的折射率会发生微小的变化，而且，共振腔的整体结构也会发生热膨胀，这都是共振腔共振波长随温度变化的因素。同时，为了放大温度对共振波长的影响，引入了一个热膨胀系数不同的金属双层膜，随着双层膜的形变，共振腔的共振波长随之发生更明显的变化。这种共振波长移动的大小可用于测量温度的变化。此外，本文采用有限元法（Finite Element Method，简称FEM）来计算共振腔的光学特性。据了解，这是第一个基于SPP共振腔热膨胀的纳米光学温度传感器，而且与同等尺度的传感器相比，其拥有较大的灵敏度。

表面等离激元；共振腔；温度传感器。

本文著录格式：宗妍，郎佩琳. 一种基于表面等离激元的纳米温度传感器[J]. 软件，2017，38（1）：06-10

0 引言

SPP是束缚在金属-介质界面上的自由电子集体震荡的耦合模式的元激发[1]。SPP有很多优良的特性，如能突破传统光波的衍射极限尺寸、在纳米量级上具有显著的局域增强效应、可以实现亚波长量级上的电磁传输与调控等[2,3]。

基于SPP的共振腔具有SPP与共振腔的双重性质。它在亚波长光学器件[4]、超高分辨率成像[5]等方面有巨大的优势。金属-介质-金属（MIM）结构因其独特的优越性，比如，局部场增强，更容易激发SPP，低弯曲损耗，结构简单，容易制造等[6,7]。因此，很多MIM结构纳米光学器件如调制器、导波管、滤波器、传感器、转换器被研发出来[8,9,10]。

温度传感器是将温度转换为其他信号的温度检测元件器件。近年来，它向着小型化、集成化方向发展。S. K. Ozdemir和G. Turhan-Sayan采用一种有温度敏感层的三层SPR结构提出了一种光学温度传感器[11]。A. K. Sharma和B. D. Gupta以集成到光纤的SPP结构提出了一种远程温度传感器[12]。目前，温度传感器主要是利用温度对折射率的影响。最近，武静等提出了一种基于SPP共振腔的光学压力传感器，这展示了一种改变SPP波导的新思维：利用外界因素使结构尺寸及其波导尺寸产生细微变化，SPP共振腔光学特性也随之改变[13]。

1 结构和方法

1.1 基本结构

在本文中，基于SPP我们提出一种新型的纳米温度传感器，其二维结构如图1所示，结构包括一个波导和一个T形共振腔，共振腔包含一个水平槽和一个竖直槽。图中虚线是T形共振腔的对称轴。波导和槽的宽度均为w，波导和共振腔之间的间隙宽度为wg，水平槽和竖直槽的长度分别为LH和LV。蓝色、灰色和白色部分分别代表银(Ag)、钨(W)和空气。共振腔上面是一层厚度为tAg的银，如图1(b)所示。这些参数的值为：w = 50 nm，wg= 10 nm，LH= 700 nm，LV= 295 nm，tAg= 50 nm。为了提高传感器的灵敏度，在银膜之上又沉积了一层金属钨，且钨膜也关于虚线对称，其厚度和长度分别为tW和LW。整个结构之外为空气。

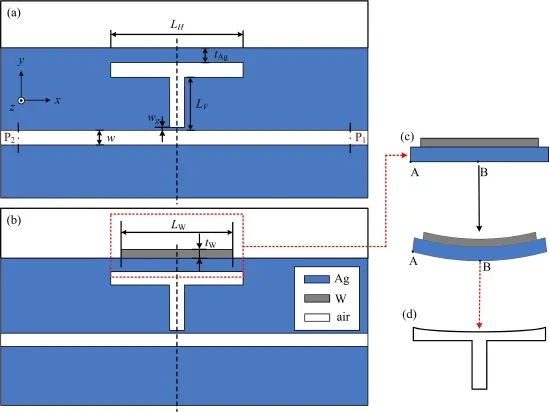
图1 温度传感器的MIM结构

1.2 结构优化

在定性处理过程中，共振腔上方的结构简化为双层膜，即银/钨双层膜。室温时，双层膜能保持平坦；温度升高时，由于两层膜的热膨胀系数不同，所以在原来的相同位置其上下膨胀程度也不同，又由于两层膜之间紧密接触，所以双层膜会发生弯曲，且会弯向热膨胀系数大的一方。本文中银的热膨胀系数比较大，所以双层膜会弯向银，即双层膜向下弯曲，这样使水平槽体积减小，如图1（c）、（d）所示。为了使传感器更加灵敏，就要使两层膜的形变差尽可能大；而只有热膨胀系数之差尽可能大，才能弯曲程度尽量明显。这就是本文选择了银和钨的最主要原因，而且这两种金属相对安全稳定。

我们需要对钨膜的尺寸进行优化，使得升高一定温度时双层膜弯曲程度尽可能明显。升高的温度设定为100℃，利用COMSOL Multiphysics的结构力学模块进行数值仿真模拟，计算升温后的弯曲程度。为了方便观测双层膜的弯曲程度，我们主要观测A、B（如图1（c）所示）两点的y方向上的位移（记作dA和dB），升温后，两点在y方向上的位移差（Δd = dB- dA）越大，双层膜弯曲得越明显。在数值仿真过程中，银和钨材料的相关的力学和热学参数如下面表1所示[14]。传感器的工作范围主要受其热学参数和其他稳定的物理性质决定。从表1中我们可以看出，银和钨的沸点分别为961.8℃和3422℃，所以最高工作温度不能超过961.8℃。而银的热膨胀系数在高于200 K即-73℃时是相对稳定的，所以，该传感器的最低工作温度不得低于-73℃。所以该传感器的工作温度范围很宽，约为-73 ºC～961.8 ºC。

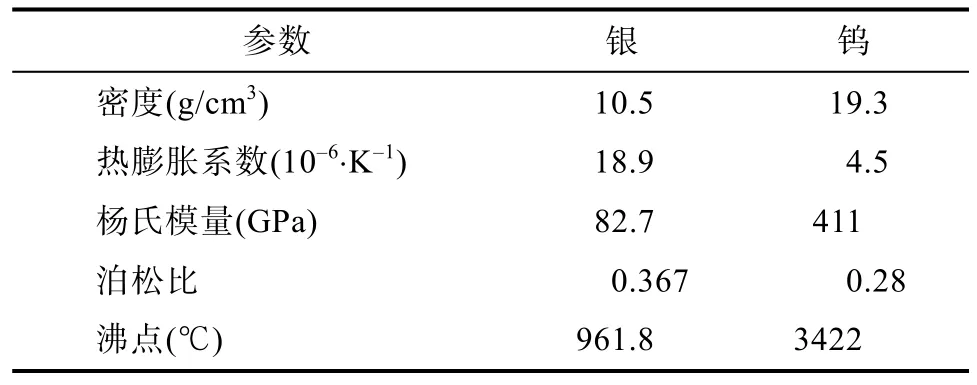
表1 银和钨的力学和热学参数

当温度升高100℃时，我们先假定钨膜的长度比银膜略短，约为600 nm，然后调整钨膜的厚度tW，计算出不同tW对应的变形，计算结果如下面图2（a）所示。可以看出，随着tW增大，dA、dB、差值Δd都先增大后减小，Δd有极大值，此时的tW= 28.6 nm。这个变化趋势的原因为：当钨膜的厚度不论特别大还是无限小时，银/钨双层膜都会近似为单层膜，这样不论温度升高多少双层膜也不会弯曲。然后我们把厚度tW固定在28.6 nm，然后调整钨膜的长度LW，计算结果如下面图2（b）所示。可以看到，差值Δd却先增大后减小，在中间某一个长度LW处出现极大值，此时LW= 609 nm。所以，当tW=28.6 nm且LW=609 nm时，双层膜的弯曲程度确实最明显。此时，当温度升高100℃时，双层膜在y方向上的最大变形可以达到约1.7 nm，如图2（c）所示。

1.3 结构的色散方程

在中长波段，SPP在银材料中的穿透深度δm不足30 nm[15]，比T形共振腔所覆盖的银膜厚度小很多，所以钨膜对整个结构的光学特性几乎没有影响，它影响的只是整个结构的力学特性。所以我们在计算整个结构的光学特性时不用考虑温度变化时钨膜折射率的改变，其折射率来自文献[16]。整个系统所有材料的磁导率为1，在MIM结构中只存在TM模式，所以SPP的色散方程为

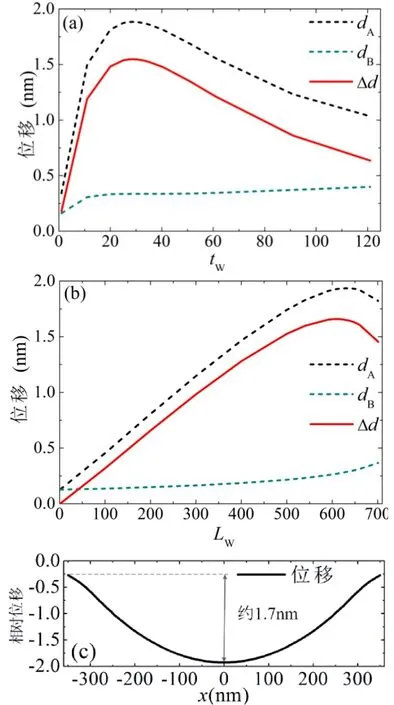
图2 温度升高100℃时，钨膜尺寸变化

1.4 金属的折射率

空气的相对介电常数为1，银的介电常数依赖于电磁波的频率，并且受到温度影响。金属的介电常数为

其中，ε∞为电子带间跃迁引起的介电常数值，也即频率无穷大时的相对介电常数，ωp是等离激子体频率，γ是阻尼常数，也是金属电子的碰撞频率，ω是电磁波的角频率。常温时，对于银，ε∞=3.8344, ωp=9.175 eV, γ=0.018 eV，我们可以因此计算出常温时银的折射率实部虚部。

然而，随着温度的变化，ε∞是常数，而ωp、γ也会随温度变化，ωp可以简化表示为[17]

其中，α是金属的热膨胀系数，T0是室温。

为了描述温度对γ的影响，我们可以把γ的影响写为γ=ωcp+ωce，其中ωcp和ωce可以分别表示为

其中，θD是德拜温度，Γ是费米面平均散射概率，△是部分逆散射，ħ是普朗克常量，EF费秘能，kB玻尔兹曼常数，θD=220 K，Γ=0.55，Δ=0.73，ħ=1.0546×10-34J·s，EF=5.48eV，kB=1.38062×10-23K-1，经过与实验数据拟合、计算，得出ω0= 0.01058 eV。这样，我们可以通过matlab计算出ωp和γ与温度的关系，由此也计算出银的折射率实部和虚部与温度的关系。

1.4 斯莱特微扰定理

根据斯莱特微扰定理[18]，如果电场占主导地位的部分增大，共振波长会发生红移。相反，如果磁场占主导地位的部分减小，共振波长会发生红移；反之，如果磁场占主导地位的部分增大，共振波长会发生蓝移。

1.5 数值仿真

在我们的仿真中，采用有限元法，选择的是COMSOL Multiphysics。SPP由平面波激发，沿着x向传播，P1和P2分别为入射端口和出射端口，仿真中采用的是散射边界条件。

2 结果与讨论

图3展示了共振腔的光学特性。通过图3（a）我们可以看出，这是一个Fano共振，我们把波长为961.5 nm处记为模式①。此处反射率出现极小值，不足0.1，后面我们对其光学特性的讨论均围绕反射率。

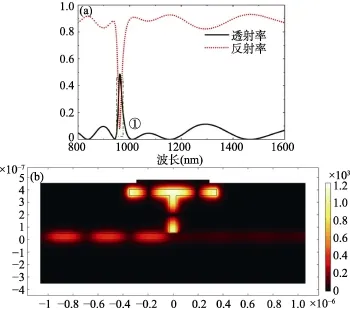
图3 （a）结构的反射谱和透射谱曲线图；（b）模式①的磁场强度|Hz|分布示意图

图4不同条件下结构光学特性的比较。图4（a）为升高不同温度时，模式①附近（图3绿色虚线框内）的透射谱；图4（b）为升温100℃时，在共振腔没有覆盖金属双层膜的情况下，模式①附近的透射谱；图4（c）为不同温度时模式①的共振波长；图4（d）为不同温度时，模式①的共振波长的移动。

图4 （a）升高不同温度时，结构的反射谱曲线图；（b）不加双层膜时，结构升温100℃前后透射谱的比较；（c）不同温度时，结构的共振波长；（d）不同温度时，结构的共振波长的移动

我们可以看出，当温度升高时，特征波长随温度均匀地移动。且当温度升高时，导致共振波长的移动主要有两大因素：折射率和体积的变化，后者又分为两部分——结构整体热膨胀和金属双层膜下凹。当没有双层膜覆盖时，其共振波长的移动远小于有双层膜覆盖时的移动，且这些移动均为红移，符合斯莱特微扰定理。

通过图4（d）我们可以看出，对于模式①，每升高25℃，特征波长移动1.7 nm。所以，我们的这个传感器的灵敏度为0.068 nm/℃。根据武静等所提出的增大共振腔尺寸来提高其压力传感器灵敏度的理论，用同样的方法，如果我们把水平槽的长度扩大两倍，那么我们的灵敏度可以增大到16倍，达到1.088 nm/℃，这样，灵敏度就已经非常大了。

3 结论

总之，通过数值仿真，采用有限元法，我们可以知道，温度升高导致SPP共振腔的光学特性的改变是由两大因素造成的——金属折射率改变和共振腔结构尺寸的改变，而后者又分为结构的整体热膨胀和双层膜外弯导致的共振腔体积变大形状微变，这些因素均导致了共振波长的红移。尤其是双层膜的影响明显放大了温度对共振波长的影响，这是共振波长红移的主要因素。由此提出的SPP光学温度传感器在相同量级的传感器中，其灵敏度占有着很大的优势。这是第一次基于SPP共振腔由于温度产生的热形变提出的传感器，这为传感器的研究提供了一种新思路。

[1] S. A. Maier. Surface plasmon polaritons at metal/insulator interfaces[M]. UK∶ Springer, 2007∶ 21-37.

[2] M. S. Tame, K. R. McEnery, S. K. OzdemW, J. Lee, S. A. Maier and M. S. Kim. Quantum plasmonics[J]. Nat. Phys., vol. 9, pp. 329-340, Jun. 2013.

[3] G. Veronis and S. H. Fan. Modes of Subwavelength Plasmonic Slot Waveguides[J]. J. Lightwave Technol., 2007, 25(9)∶ 2511-2521.

[4] D. K. Gramotnev and S. I. Bozhevolnyi. Plasmonics beyond the diffraction limit[J]. Nat. Photon., 2010, 14∶ 83-91.

[5] S. Kawata, Y. Inouye, and P. Verma. Plasmonics for near-field nano-imaging and superlensing[J]. Nat. Photon., 2009, 3(7)∶388-394.

[6] Y. X. Xiang, X. Z. Zhang, W. Cai, L. Wang, C. F. Ying, and J. J. Xu. Optical bistability based on Bragg grating resonators in metal-insulator-metal plasmonic waveguides[J]. AIP. Adv., 2013, 3∶ 012106-1-012106-7.

[7] G. Veronis and S. H. Fan. Bends and splitters in metal- dielectric-metal subwavelength plasmonic waveguides[J]. Appl. Phys. Lett., 2005, 87∶ 131102-1-31102-3.

[8] X. Chen, R. Zhang, P. L. Lang, H. C. Yang, T. Zhong and K. Zhong. Transmittance spectrum of surface plasmon polariton based filter with asymmetric double-ringresonator and switch[J]. J.Mod. Opt., 2014, 61(9)∶ 716-720.

[9] Z. Chen, X. K. Song, G. Y. Duan, L. L. Wang and L. Yu. Multiple Fano Resonances Control in MIM Side-Coupled Cavities Systems[J]. IEEEPhoton. J., 2015, 7(3), Art ID. 270100.

[10] Z. Chen, L Yu, L. L. Wang, G. Y. Duan, Y. F. Zhao and J. H. Xiao. Sharp Asymmetric Line Shapes in a Plasmonic Waveguide System and its Application in Nanosensor[J]. J. Lightwave Technol., 2015, 33(15)∶ 3250-3253.

[11] S. K. Ozdemir and G. Turhan-Sayan. Temperature Effects on Surface Plasmon Resonance∶ Design Considerations for an Optical Temperature Sensor[J]. Lightwave Technol, 2003, 21(3)∶805-814.

[12] A. K. Sharma and B. D. Gupta. Theoretical model of a fiber optic remote sensor based on surface plasmon resonance for temperature detection[J]. Opt. Fiber Technol, 2006, 26(87-100).

[13] J. Wu, P. L. Lang, X. Chen, and R. Zhang. A novel optical pressure sensor based on surface plasmon polariton resonator[J]. J. Mod. Opt, 2015, 63(3)∶ 219-223.

[14] Marvin J. Weber. Handbook of Optical Materials[M]. USA∶CRC Press LLC, 2003∶ 4.3-4.4.

[15] A. Amrani, B. Bouhafes, “Plasmon-Polaritons And Their Use In Optical Sub-Wavelength. Event Of Copper And Silver”, IJRAP., vol. 2, no. 2, pp. 9-15, May 2013.

[16] Marvin J. Weber. Handbook of Optical Materials[M]. USA∶CRC Press LLC, 2003∶ 4.2.

[17] J. A. McKay and J. A. Rayne. Temperature dependence of the infrared absorptivity of the noble metals[J]. Phys. Rev. B, 1976, 13(2)∶ 673-684.

[18] 王一平. 工程电动力学[M]. 西安∶ 西安电子科技大学出版社, 200∶ 35-36.Wang, Y. P. Engineering Electrodynamics[M]; University of Electronic tecknology press∶ Xi’An. China, 2007, pp 35-36(in Chinese).

An Optical Temperature Sensor Based on Surface Plasmon Polariton Resonator

ZONG Yan, LANG Pei-lin

(Beijing University of Posts and Telecommunications, Beijing, 100876, China)

This paper presents a novel optical temperature sensor based on a nanoscale surface plasmon polariton (SPP) resonator. With the increase of temperature, the refractive index of the metal will have small changes, and thermal expansion will occur throughout the structure of the resonant resonator, these are the factors that result in the shift of the resonators’ resonance wavelength with the temperature changing. At the same time, in order to enlarge the temperature's influence on the resonant wavelength, a metal bilayer with different thermal expansion coefficient is introduced, with the deformation of the bilayer, the resonator’s resonance wavelength then will change more obviously. The size of resonance wavelength can be used to measure the changes of temperature. In addition, The Finite Element Method (Finite Element Method, FEM for short) is applied to calculate the optical properties of the resonator. As is known to all, it is the first nanoscale optical temperature sensor based on the thermal expansion of the SPP resonators, and compared with the same scale of sensor, it has greater sensitivity.

SPP; Resonator; Temperature sensor

O436.2

A

10.3969/j.issn.1003-6970.2017.01.002

中国国家自然科学基金NO.11374041, 11574035

宗妍，女，硕士研究生，主要研究方向：温度对SPP共振腔的影响及其应用研究；郎佩琳，男，副教授，主要研究方向：表面等离激元共振腔及其应用，纳米光学传感器、光纤传感器和光学创新元素。

宗妍，硕士研究生，主要研究方向：温度对SPP共振腔的影响及其应用研究。