计算机图形学中仿射变换的教学

2017-02-27章夏芬朱昌明

计算机教育 2017年2期

关键词：矢量绘制立体

章夏芬，朱昌明

（上海海事大学信息工程学院，上海 201306）

计算机图形学中仿射变换的教学

章夏芬，朱昌明

（上海海事大学信息工程学院，上海 201306）

针对计算机图形学中三维立体绘制和变换涉及的数学理论太多、内容抽象、难以理解、难以综合应用的问题，分析三维仿射变换的数学基础、难理解的理论点、综合应用难点，提出浅入深出的理论讲解法，用实践综合和拓展法相结合的方式启发学生对综合变换应用的设计兴趣，为计算机图形学讲授仿射变换的教学者提供教学思路和参考。

计算机图形学；三维仿射变换；浅入深出；综合拓展

0 引言

仿射变换(Affine Transformation)及综合应用，尤其是三维 (Three-Dimension, 简称3D)仿射变换是计算机图形学中最重要的部分，是3D立体重建、科学计算可视化的基础，广泛应用于工程设计、医学图像、实时绘制、自然景物仿真、计算机动画、虚拟现实及影视特效等领域中。仿射变换与数学联系密切，通过操纵矩阵变换实现，理论难度大，教学学时有限，如果处理不好，满屏幕的数学公式和矩阵，会使学生难以理解，失去兴趣，影响教学质量。

受硬件限制，以往计算机图形学所处理的图形大都是二维的(Two-Dimension, 简称2D)。但随着计算机图形学的发展，Microsoft最早推出能捕捉3D坐标信息的Xbox+Kinect，Intel接着推出了RealSense 3D摄像头。3D图形绘制越来越普及，3D电影已“飞入寻常百姓家”。计算机图形学的教学要与时俱进，需要讲解3D图形绘制和变换。

本科生在实验中能绘制出3D图形是有成就感的，但对具体操作过程中遇到3D立体级联变换、消隐及相应的矩阵变换，觉得难理解，影响后续综合应用。有些学校在本科生的计算机图形学课程中，只简单介绍3D知识点[1]。本科生对仿射变换的迷茫主要体现在：①能理解3个基本的仿射变换对应3个矩阵，但难理解3D综合变换到底由几个基本仿射变换组成、顺序是什么；②能调用OpenGL函数完成单一的基本变换，但没掌握好原理，无法应用在具体的综合变换中。

1 浅入深出法

国内外很多大学以Edward Angel撰写的《计算机图形学》[2]为教材，笔者也以此书原版为教材[3]。该教材中，仿射变换是直接从3D基本仿射变换（包括平移、缩放、旋转）开始，把2D仿射变换作为3D的一种特例，放在课后练习题里。然而，3D基元变换矩阵含4×4个元素，综合变换对应矩阵的连乘。本科生刚开始接触，难以把实际空间的变换和相应的矩阵理论对应起来。因此，课堂讲解时宜由浅入深、循序渐进，主要表现在以下3方面。

（1）发挥图形学特长，用图例说明空间点、矢量、标量对应的物理意义。由线性变换公式引出矩阵运算；先讲解“为何2D变换矩阵是3×3矩阵”，为理解3D变换矩阵是4×4矩阵奠定基础。

（2）颠倒教材中3D和2D仿射变换内容的顺序。对教材中略过的2D变换，做出辅助图示详细讲解；而对教材中详细展开的3D变换，则只讲概要，讲解3D与2D变换的不同之处。

（3）扩展仿射变换，进行综合应用。从空间一个点的变换，扩展到空间的一条线段，再扩展到用线段表达的3D物体，最后进入3D级综合变换。

1.1 相关数学原理

何援军在文献[4]中指出：计算机图形学和造型依赖于点和向量的数学运算，仿射变换也依赖点和向量的运算。广义而言，仿射变换涉及欧几里得空间的3个基本元素：点（points）、矢量（vectors，又称向量）和标量（scalars）。在讲解点、矢量、标量3个元素绘图的表达和运算时，无需一开始就深入讲解相关数学原理，较难理解的数学原理容易打击学生的兴趣。

在讲解点、矢量、标量表达和运算时，并不按线性代数的方式讲解，而是发挥图形学的优势，辅助图示说明。让学生回答PPT上某一个点到底有多长，引出Points在数学和计算机图形学中的区别：图形学的Points需要绘制，要知道Points的尺寸和形状；让学生回答PPT上的某两点到底有多远，引出描述距离Scalars；接着指出Scalars只描述大小、尺寸，无法描述空间位置关系，引出Vectors，强调Vectors的两个属性（方向和模长），用图示意。

接着，用1个学时以图示辅助讲解Vectors的加、减、乘等操作的物理意义，着重讲解乘分为点乘（dot product）和叉乘（cross product）。在讲解Vector叉乘运算时，引出同一个面的两个Vectors的叉乘运算结果是Vectors，重复强调Vectors的两个属性；提出法矢量（Normal）的概念，为后续3D物体消隐算法中面的法矢量计算奠定基础。在展示Vectors的点乘运算公式时，指出该运算结果的符号取决于两个Vectors的夹角。若夹角θ∈[-90°, 90°]，则结果是正值，为后续3D消隐算法中判定面是否可见奠定基础。

1.2 2D仿射变换

教师演示一个2D的点在笛卡尔坐标系中的变换，向学生提问：如何计算变换前后的坐标位置？引出计算一个点仿射变换的坐标位置计算方法，并用矩阵表示；接着，展示较复杂变换是上述3种仿射变换的综合；然后，指出“由多个像素点所表达的物体，其中一个点是怎么变换的，该物体上的其他点做相同变换，和同一个变换矩阵做相乘”。

1.2.1 基本2D仿射变换

用动画图示，在PPT展示物体的平移变换。该物体中的一个点(x,y)在笛卡尔坐标系统中平移(Tx,Ty)距离后，新位置的坐标值(x’, y’)可由公式表达。结合上文讲解的Vectors和Points，从方便计算机编码的角度出发，增加一个维度（值为0时是Vectors，值为1时是Points），得出2D的仿射变换矩阵是3×3矩阵。把矩阵元素个数为何多出一维，放在2D仿射矩阵中讲解，是因为2D的图示效果比3D更直观，2D变换矩阵元素少，更易理解。同理，讲解2D的缩放和旋转。

在同一屏幕呈列并比较2D的3个基本仿射变换矩阵，称之为“三板斧”。类比计算机色彩系统中的RGB“三板斧”，RGB三基色能混合出任意一种颜色。这使学生联想到：RGB能按一定比例混出新颜色，3种基本变换能按一定规矩级联出任意一种空间变换。

1.2.2 级联2D变换

RGB三基色按一定比例混合得任一种颜色，3种基本仿射变换按一定顺序级联变换得到空间任意一种复杂变换。类比体操运动员完成复杂表演时，每个基本动作顺序不能交换，空间上的物体从初始状态变换到最终状态的每个基本变换序列，顺序也不能交换，可用图示给反例证明。接着，教师展示矩阵级联相乘中，乘子是不能交换的。最后，讲解综合变换：从两个矩阵的级联开始，图示物体初始状态变换到最终状态分解成两个动作，每个动作都对应一种基本仿射变换矩阵；推广3个矩阵的级联变换、 4个矩阵的级联变换等。

1.3 3D仿射综合变换

以上详细讲解2D仿射变换，为3D仿射变换奠定基础，尤其是3D的综合变换。3D增加了一维（用z表示），3D的平移和缩放，是在2D变换矩阵基础上添加变量Z。应重点讲解3D的旋转变换与2D不同，讲解3D的绕X轴、绕Y轴和绕Z轴旋转，并讲解教材上第200页的实例，即绕3D空间任意轴旋转θ°，强调正负方向，如果方向反了，代入级联矩阵中的角度正负值不同，结果就不同。教材上并没给出方向定位方法，需要补充定位的依据和图例，即平面的法矢量和时钟旋转方向。图示一种可行方案，从平面法矢量的正向（右手规则，在幻灯片上以水面上的灯塔示意）往下看水平面，逆时钟方向为正方向。

1.4 面消隐藏

绘制过程中3D物体由多个面构成，其仿射变换涉及面消隐。用肢体语言展示，前方的面，眼睛能看得见；背后的面，眼睛看不见，进而引出最简单的凸面体消隐算法——后向面检测法(Back-face detection)。检测一个面是否可见有3个步骤：①计算面的法矢量；②计算视线矢量；③两个向量做点乘，根据正负值决定是否可见。

如何计算面的法矢量？回顾刚讲过的矢量点乘和叉乘运算：两个矢量叉乘的结果，其方向垂直于这两个矢量构成的面。而获取两个矢量，只需要找到给定面的3个点，两两做差可得到两个矢量。这两个矢量做叉乘，其结果为该面的法矢量。

如何计算视线的方向？回顾刚讲过的空间上两个点做差运算：用眼睛所在的点和眼睛所看的点，做差运算，其结果是视线方向，一定要注意矢量方向。

2 实践验证法

通过上述理论讲解，学生可基本理解3D变换的原理。但根据笔者的教学经验，理解原理和独立编码、实现3D变换综合应用存在着距离。因此，秉承浅入深出法，从简单3D立体仿射变换实验着手，能使学生只专注原理和步骤。简单表现在：①输入数据简单，3D立体用8个3D点表达；②所用工具简单，用VC++（或Turboc）作为编码工具，禁止调用OpenGL库函数，避免OpenGL的加载；③绘制的结果简单，仅绘制12条直线段表示3D立体，避免了曲线、渲染等复杂算法和相关绘制。

2.1 3D物体绘制

编码之前，教师先演示并讲解3D物体投影到2D屏幕上的正等测投影法（Axonometric）的由来、推导过程，顺便为下一章的投影算法奠定基础。在推导正等测投影矩阵过程中，详细展示以下3个动作：①绕Z轴转 θ°；②绕X轴转-Φ°；③投影到XOZ平面。在这个展示过程中，给出相应的变换矩阵，再次证明一个基本变换动作对应一个基本矩阵。

以点P(x, y, z)为例，该点乘以投影矩阵，其结果是一个只含x和z坐标值的点。把这个规律写成函数，其他7个点调用该函数，得出由8个点组成的简单3D立体在2D屏幕上的投影坐标值。设计由8个点构成的3D立体时，可使其中一条边比另一条边高，并对8个顶点标记编号，这会使3D立体变换的前后位置明显。绘制后的可视效果见图1（b）。

图1 3D立体绘制

2.2 3D物体变换

屏幕上绘制的一个物体，怎样确认它是3D的呢？答案是让物体运动起来，使用户不仅能看到该立体的前面，还能看到后面，进而引出物体运动分3类。教师重复给出仿射的3个变换：平移、旋转和缩放的矩阵，将各个变换编码成一个函数。

然后，编写交互方式，用5对键盘按键对应5种变换：绕X轴旋转、绕Y轴旋转、绕Z轴旋转、缩放、平移。

2.3 3D物体消隐

由12条线6个面构成的3D立体，若所有轮廓线都用实线绘制，则难以辨别哪个面是前面、哪个面是后面。因此，要对面进行隐藏，隐藏面的轮廓线用虚线绘制，可见面的轮廓线用实线绘制。

可通过问题“如何处理虚实面的公共边”引出解决方案：先用虚线画不可见面的轮廓线，再用实线画可见面的轮廓线；通过问题“如何验证消隐算法是正确的”引出验证方式：用5对按键触发5种变换，观察3D立体在变换中的消隐是否正确。如图2所示，3D立体绕Z轴旋转一个角度，旋转之前，由顶点2和6组成的边是虚线，代表不可见，由顶点1和5组成的是实线，是可见的，见图2（a）；旋转一个角度后，2和6的边是实线，从“不可见”变成“可见”，而1和5组成的边则反之，见图2（b）。

图2 3D立体绕Z轴旋转的消隐

3 综合拓展法

按上述方式把仿射变换讲完整，需要7个学时，各内容的分布见表1。

表1 仿射变换教学的学时分布

3.1 综合应用

杭后俊在文献[5]中提出，计算机图形学教学的实践不足，即使有实验，也是验证性实验。蒋先刚在文献[6]中提出，兴趣是最好的老师。因此，需要设计一个接近生活实践、不重复教材内容、能综合应用算法的绘制实例。笔者给出旋转和平移两种仿射变换的综合应用——小汽车的行驶（车轮在旋转而车身在平移）。设置平移和旋转的参数，使车轮转动一圈后，整个车身前进的距离等于车轮的周长。为了不被其他因素干扰，只用简单轮廓线表示车模；为了使车轮旋转明显，绘制多条线段表示车轴，如图3所示。

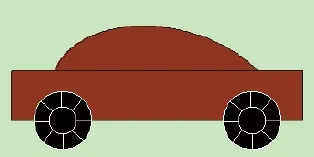
图3 仿射变换综合应用示例

3.2 拓展应用

乔布斯（Steve Jobs）在斯坦福大学演讲时说：把知识点串接一起(connecting the dots)。串接在一起后能得到教材上没有的新应用，能让学生见识到所学知识在实际场合中的应用。在后续曲线绘制时，让学生直接在已有作品上更新：画两条Bezier曲线表示的弯曲道路，并使车模由参数控制沿曲线前进，而不是沿直线前进。学完分形后继续更新：在弯曲的道路两旁，应用分形算法绘制树木。如此，每学习一次图形学，都能更新、完善原有的场景和物体，一步一步接近真实世界。这会使计算机图形学的学习过程，像游戏升级那样具有挑战。

上述3D物体仅由有限顶点构成，真实世界的3D物体由更多点构成，但变换的原理是一样的。建议学生可在后续的毕业设计中进一步完善，绘制出更逼真的3D物体。

最后十分钟，教师在屏幕上显示同一个汉字旋转、缩放、平移后生成的多幅不同图像，提出问题“不同的图像，如何证明它们是同一个字”，并说明这些图像均是原图乘以变换矩阵所得，是模式识别要解决的问题，但和图形学密切相关。通过这种关联方式，进一步拓展学生的思维，为培养其自学能力奠定基础。

4 教学效果与讨论

在笔者10年的计算机图形学教学中，前6年对仿射变换的讲解是按教材章节顺序进行的，效果一般。后4年改变方式，以“要解决的问题”和实践为导向，重组章节顺序，用浅入深出法讲解，收获了学生的学习热情。这是因为由浅入深法，即使差生也能听懂前半部分，不至于在开始不久后便失去兴趣；后半部分较复杂，但有实践例子相辅，在简单基础上，每次仅增加一个新功能，一步步形成复杂的综合变换，激发学生的挑战心理。笔者的授课班上，部分学生在后续本科毕业设计时选择了图形绘制相关的课题（如3D书法匾额设计、3D书法字匹配点可视化），因为学生通过该门课程的学习有信心完成较难的项目。

仿射变换涉及较多的数学知识，讲解时若以数学运算为重，不仅会冲淡计算机图形学的绘图目的，而且会使学生产生“前奏部分都听不太懂，后续怎能学好”的感觉。因此，教师不要一次性把跟仿射变换相关的数字知识讲得很透彻、很详细，而是结合后续要解决的问题多次回顾。实验验证前，再次回顾并加入只针对这项运算的详细讲解，以实图示之。这种回顾貌似在重复相同的原理，但并非简单重复，而是从不同角度、不同应用讲解同一个知识，能加深记忆和理解。在这种教学方式下，本科生反馈：原先只知道点乘、叉乘的公式定义，学了仿射变换后，知道了它们的物理意义，很有成就感。

傅向华在文献[7]中提出以实验和项目为主，要求学生撰写不少于5 000字的实验报告，其提出的过程性考核，值得提倡。但是，让本科生撰写5 000字的实验报告，容易因耗费过多时间写长篇报告而使学生厌倦。因此，在仿射变换实验完成后，笔者仅要求学生撰写1～2页的小报告，概要描述完成该实验是如何实现的，可用伪代码描述，也可用自然语言描述。