基于PSO的工业机器人时间-脉动最优轨迹规划

沈 悦，李银伢， 戚国庆，盛安冬

(南京理工大学 自动化学院，江苏 210094)

基于PSO的工业机器人时间-脉动最优轨迹规划

沈 悦，李银伢， 戚国庆，盛安冬

(南京理工大学 自动化学院，江苏 210094)

为提高工业机器人的工作效率，并且保持机器人关节平稳运动，提出一种基于粒子群优化算法的时间-脉动最优轨迹规划方案；通过权重法将多目标优化转化为单目标优化，再运用粒子群优化算法得到时间-脉动最优的运动轨迹；轨迹规划中，采用了关节空间五次非均匀B样条插值法，以确保脉动曲线的连续性；最后以GRB4016工业机器人为研究对象进行仿真实验，结果表明，该方案可以得到较理想的运动轨迹，并验证了方案的有效性。

B样条曲线；粒子群优化；时间-脉动最优；轨迹规划

0 引言

工业机器人的轨迹规划是轨迹跟踪控制的基础，对工业机器人的工作效率、平稳运动、能量消耗等均具有重要意义，所规划的轨迹函数都必须是连续和平滑的，从而使得工业机器人能平稳的运动。工业机器人的轨迹规划可分为笛卡尔空间(也即工作空间)轨迹规划和关节空间轨迹规划[1-2]，笛卡尔空间轨迹规划能够直观的观察到工业机器人末端的运动轨迹及其位姿，但是，这种方法不能回避运动学奇异点的问题，从而给运算带来了很大的麻烦；而关节空间的轨迹规划方法则不存在这种问题。本文主要探讨的是关节空间的轨迹规划方法。如今，关节空间的轨迹规划方法常用的有抛物线过渡的线性插值法[1-2]、多项式插值法[3-4]、B样条插值法[5]等插值法，和从加速度曲线出发的矩形加速度曲线法、梯形加速度曲线法、正弦加速度曲线法及其组合法等[6]。其中，多项式插值具有阶次高、没有凸包性的缺点；矩形加速度法具有加速度曲线不连续的缺点；梯形加速度法具有加加速度曲线不连续的缺点；而B样条曲线可以分段处理、具有局部支撑性、凸包性和导数连续性，应用广泛，效果明显优于其他插值法。

关节空间规划的轨迹优化[7]根据性能指标划分可分为时间最优[8-9]、脉动(即加加速度)最优[10-11]、能量最优[9]、距离最短等，其中时间最优算法是最早提出的。优化方法大多采用免疫算法[8]、遗传算法[12]、粒子群算法等进化算法，以及上述算法的改进或混合算法。近年来，粒子群优化算法(PSO，particle swarm optimization)得到诸多研究学者的关注。相较于遗传算法，粒子群算法具有参数设置简单、易调节，算法简单、易实现等优势。

B样条曲线具有局部支撑性、凸包性以及导数连续性等优点，而粒子群算法则具有参数设置简单、易调节，算法简单、易实现等优势。因此，为提高工业机器人的工作效率，并且保持机器人平稳运动，本文提出一种基于PSO(particle swarm optimization)算法的五次B样条插值的工业机器人轨迹规划方法。具体的，先预设关节路径点，再进行五次B样条插值，得到C4连续的轨迹曲线，以确保脉动函数(即加加速度jerk函数)连续；然后运用PSO算法，以路径点之间的时间间隔序列为粒子向量，考虑约束条件(速度、加速度、加加速度等)，最终达到优化的目的。

1 问题描述

关节空间点到点(PTP，PointtoPoint)轨迹规划，即根据工作任务，得到一系列工作空间机械臂末端的期望路径点，再根据逆运动学运算得到关节空间相应的关节角，最后对所得关节角路径点进行插值运算，以关节角的函数来描述轨迹(时间和空间)。

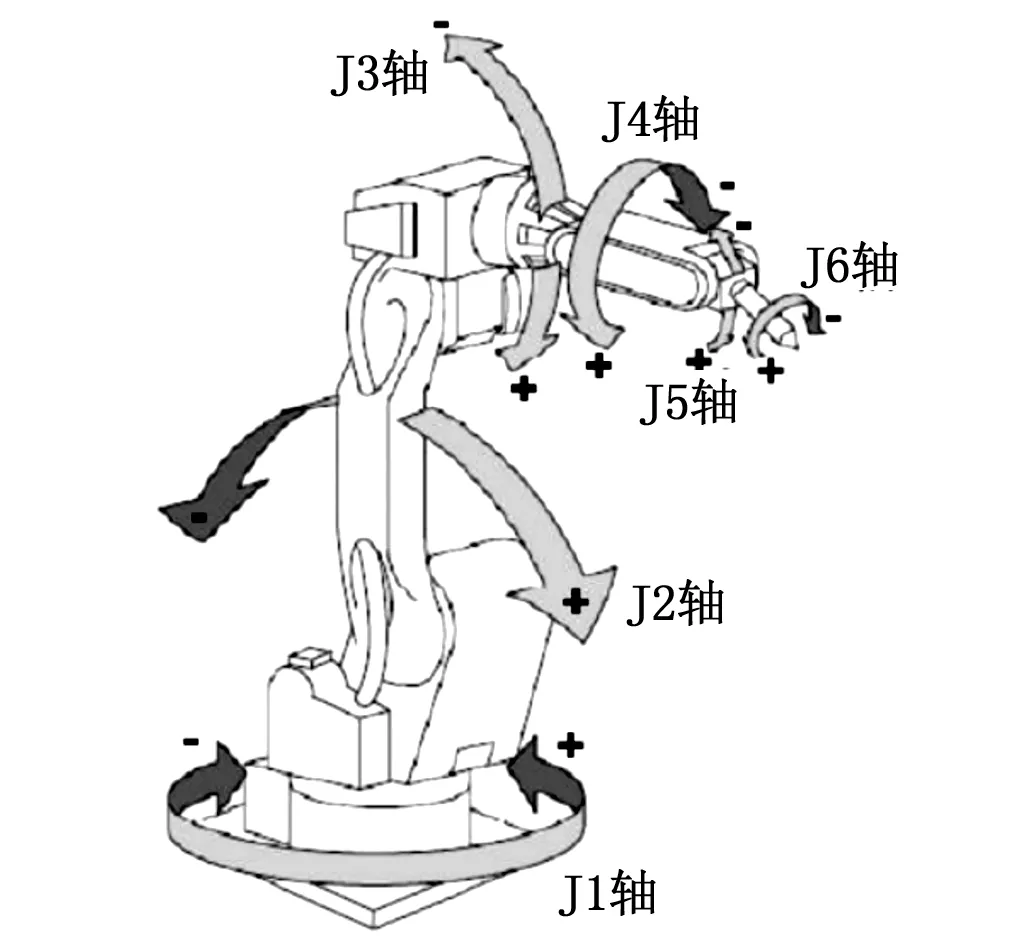
图1 GRB4016工业机器人模型

(1)

相应的速度、加速度、加加速度(脉动)函数表示如下：

(2)

(3)

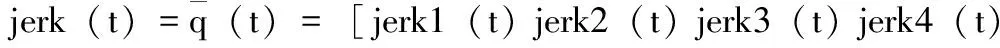
jerk5(t)jerk6(t)]T

(4)

进行轨迹优化过程中，为实现工业机器人关节空间轨迹规划的优化，从机器人的运行效率和轨迹平滑性出发，定义如下性能指标：

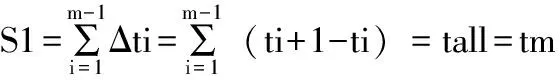
(5)

(6)

上式中，S1为机器人关节轨迹运行总时间，也可用tall或tm表示，用来衡量机器人运行效率，m为预设路径点个数，i为路径点序号；S2为机器人关节平均脉动，用来衡量机器人轨迹平滑性，其中，N为关节数，本文N=6，j为关节序号，jerkj(t)为j关节的脉动函数，可由式(4)求得。

2 五次B样条函数构造

本文在关节空间运用非均匀B样条对关节路径点进行插值，第j关节第i段k次非均匀B样条插值的轨迹可描述为：

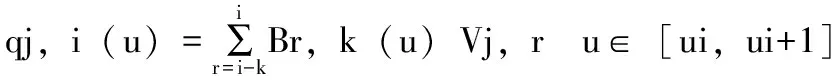
(7)

式(3)中Vj,r为j关节的控制点，共有1+k个控制点来定义该段轨迹，那么m-1段轨迹则有m-1+k个控制点，上述控制点可由已知路径点反求得到；Br,k(u)为k次规范B样条基函数，其每一个可称为规范B样条，有如下定义[5,13]：

(8)

(9)

为下文进一步分析轨迹的速度、加速度、加加速度曲线以及边界条件，利用下式可递推求得相应的阶控制点，进而得到轨迹的阶导数[13]：

(10)

本文中预期得到脉动(加加速度)连续的轨迹，采用了C4连续的非均匀五次B样条插值法，因此得到的轨迹也是C4连续的。将k=5代入上述相关公式进行运算，针对j关节进行求解。对m+4个控制点进行反求，需要列出m+4个方程，其中m个方程可由已知路径点列出：

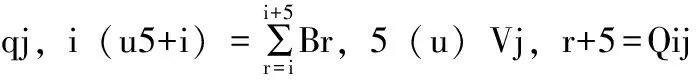
(10)

(11)

最后可列出矩阵方程

AjDj=Pj，解得Dj=Aj-1Pj

(12)

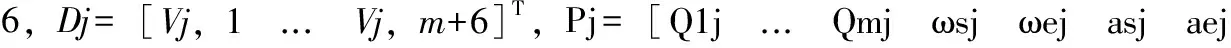
3 基于PSO的最优时间-脉动求解

根据第1章节中定义的性能指标，将时间-脉动最优这一多目标优化，运用权重法转化为单目标优化，得到算法所需的适应度函数如下：

fit=a·S1+b·S2

(13)

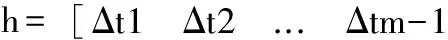
基本粒子群算法的描述及其各项参数定义如下[14-15]：

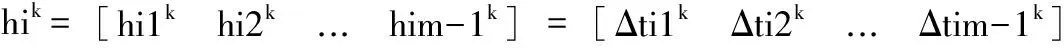
(14)

式(12)中参数按经验选取：加速因子c1=1.49,c2=1.49，惯量因子ω=0.729，r1,r2为[0,1]之间的随机数。pidk为粒子个体位置最优值，pgdk为群体位置最优值。

基于PSO的五次B样条轨迹规划方案的具体步骤如下：

1)根据经验初始化粒子群规模N，惯性因子，加速因子等，一般地，N=20；

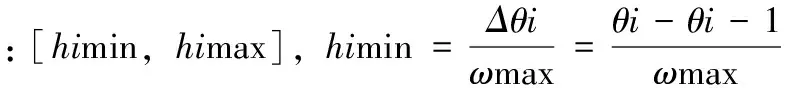
3)根据式(14)来更新粒子的速度向量和位置向量，超出搜索范围的用该维数的最大值或最小值代替；

4)根据式(13)计算粒子当前位置的适应值，更新粒子历史最优位置pidk和群体最优位置pgdk；

5)若满足优化条件则停止迭代；由于本文所求没有优化条件，需设置最大迭代次数DTMax，以确保算法达到收敛状态，若未达到最大迭代次数，则需返回步骤③。

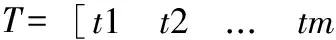
4 仿真与实验结果分析

为验证基于PSO的五次非均匀B样条曲线插值轨迹规划方案的有效性，即能得到运行时间S1较短、加加速度(脉动)曲线连续以及平均脉动S2较小的轨迹，并且探讨将多目标优化转化为单目标优化的适应度函数中S1、S2的权重系数的取值对上述两种指标优化结果的影响，本文以GRB4016型六自由度工业机器人为研究对象，如图1所示，其各轴运动范围和运动约束(见表1)，预设8个路径点(见表2)，在关节空间进行基于PSO算法的五次非均匀B样条轨迹规划。

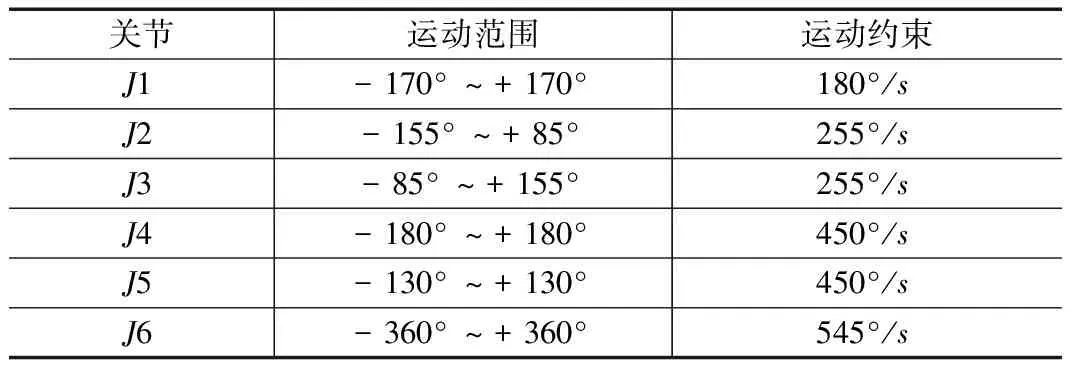
表1 轴运动范围及约束

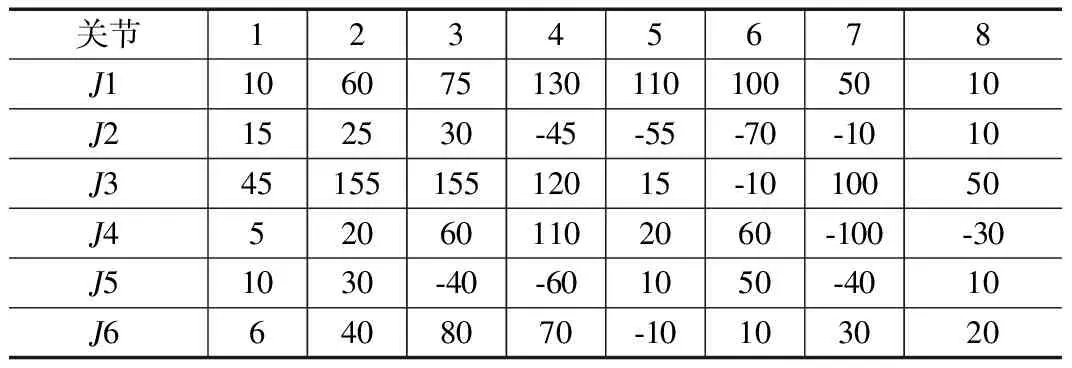
表2 关节路径点 (单位：度)

在进行五次非均匀B样条轨迹规划时，需进行7段轨迹的规划，时间序列长度为7。则运用PSO算法进行优化中，粒子的维数为7，设有20个粒子，DTMax设为100，加速因子、惯性因子等其他参数均按第三章所述设定，再设定不同的权重系数值a,b(a+b=1)，最后进行多次仿真实验得到时间-脉动优化的结果如表3。

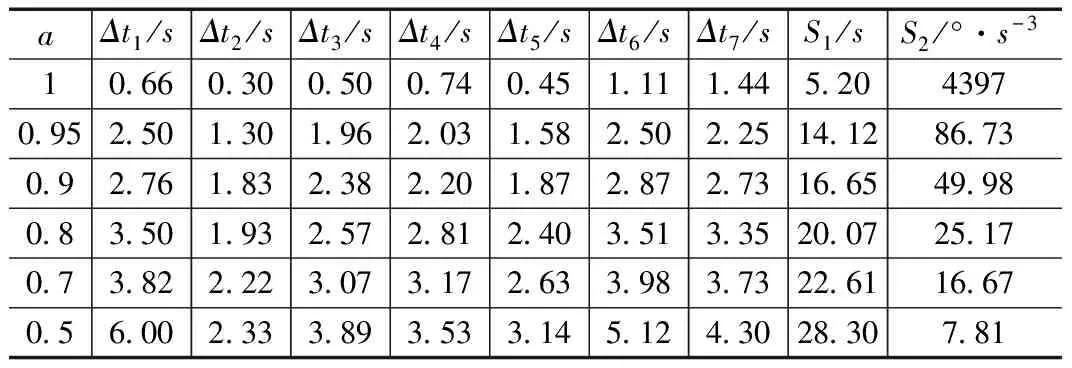
表3 基于PSO的时间-脉动优化时间序列及性能指标

由表3可知，a的值越大，权重就越大，S1就值越小，表明优化效果越明显；同理，b的值越大，权重越大，S2值越小，其优化效果越明显。其中对于变化幅度而言，随着a的减小，相较于指标S1的增加的幅度，指标S2的下降的幅度较大，说明权重变化对指标S2的影响较大。具体的，a=1时，S1指标值(即工业机器人运行时间总和)可以达到一个较小的值，但由于没有对S2(即加加速度平均值)进行优化，S2数值较大；当S2的比例大于0.05，其值就基本稳定在几十的范围内，因此结合指标S1，选取加权指标较小的第三组数据(a=0.9,b=0.1)进行五次非均匀B样条插值，从而得到各关节的位置曲线(关节角变量曲线)、角速度曲线、角加速度曲线、角加加速度(脉动)曲线，如图2～图5所示。

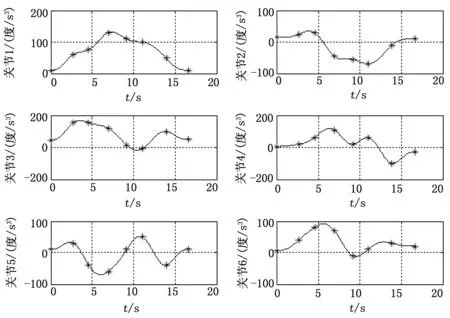
图2 各关节位置曲线及路径点

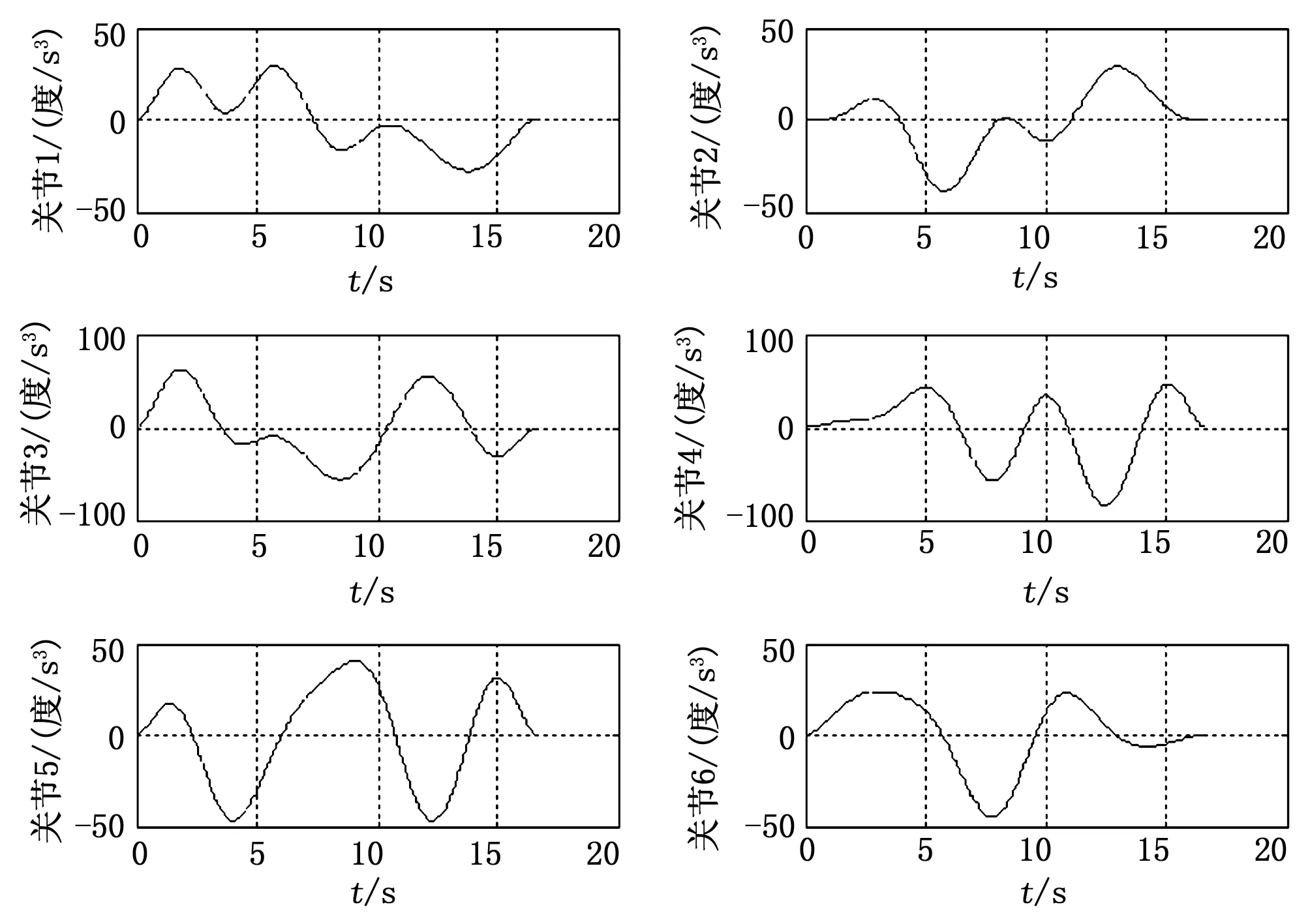
图3 各关节角速度曲线

图4 各关节角加速度曲线

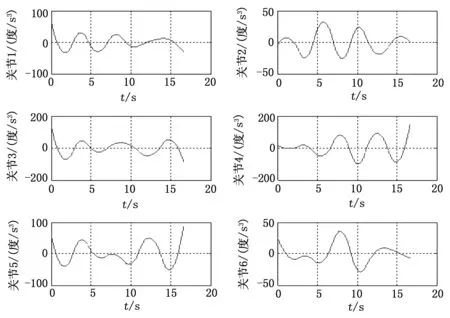
图5 各关节脉动曲线

由图2可知根据上述算法所得的各关节轨迹均能通过设定的路径点(“*”表示关节空间路径点)；由图3可知，各关节的角速度均在约束条件范围内；由图3、4可知，轨迹的启停角速度、角加速度均为零；由图4、5可知，得到的关节角加速度、角加加速度曲线均连续。

综上，基于PSO算法的五次B样条能得到运行时间较短、脉动连续且平均脉动较小的运动轨迹，确保了机器人较高的工作效率以及较高的平稳性。

运用正运动学计算出机器人执行器末端的轨迹，再利用MATLAB中的RobotToolbox可绘制出该机器人的三维模型，如图6和图7所示。

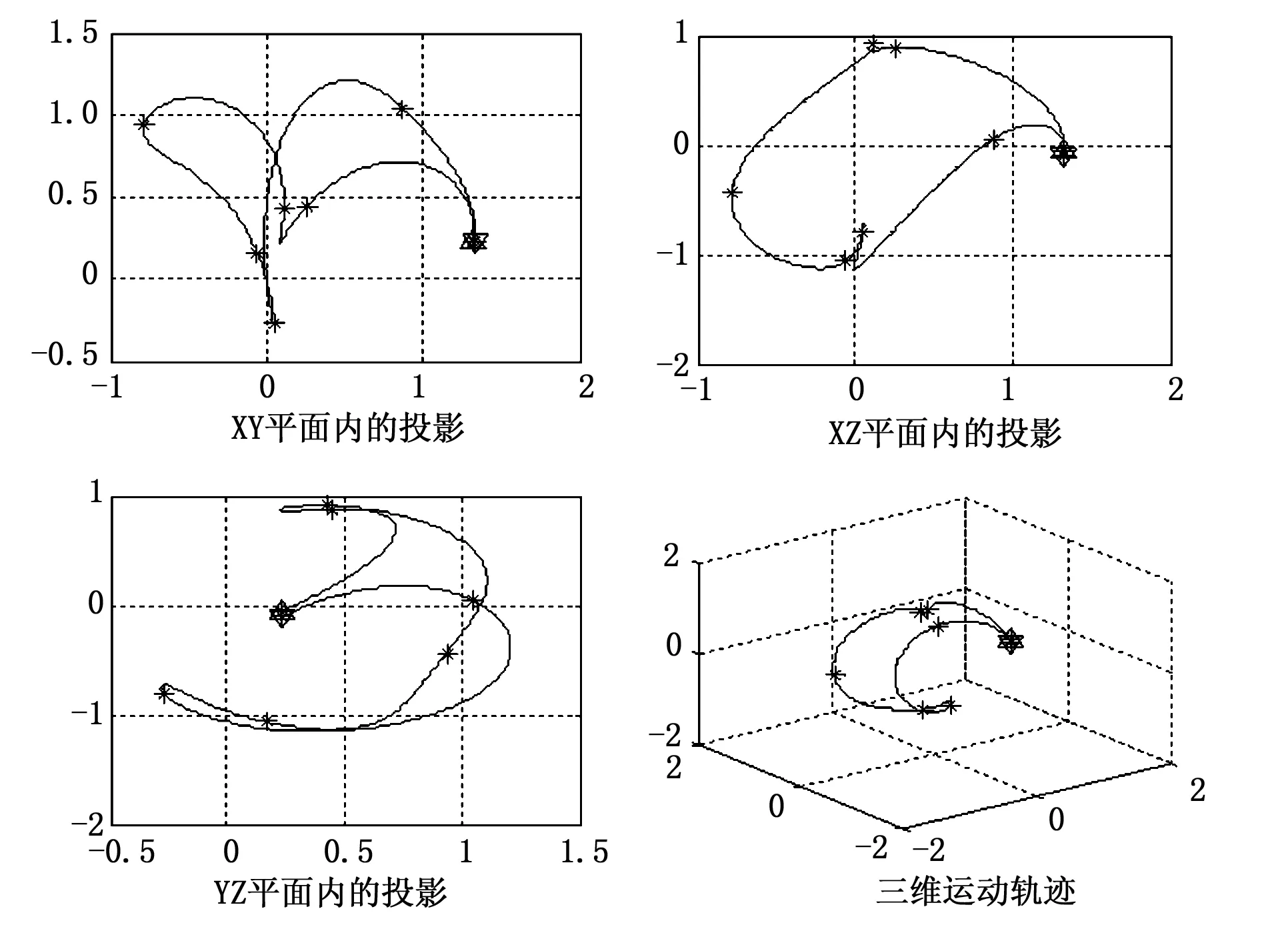
图6 六自由度机器人执行器末端运动轨迹

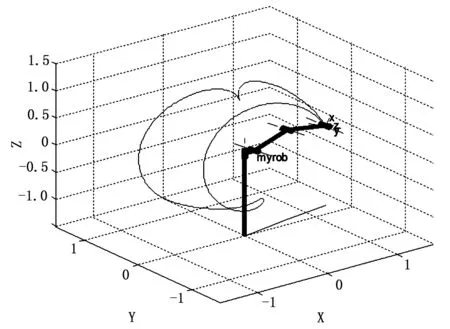
图7 GRB4016工业机器人三维模型

图6中，“＊”代表路径点，“△”上三角代表起始点，“▽”下三角代表终止点，可看出，起止点基本重合。图7为在MATLAB的RobotToolbox建立的GRB4016型号工业机器人的三维模型。

5 结论

本文运用了五次非均匀B样条插值法，来进行关节空间的轨迹规划，这种插值法相较于高阶多项式插值法，具有凸包性和局部支撑性等优点。并通过PSO算法对规划出的轨迹进行时间-脉动最优的优化。研究结果表明，本文提出的基于PSO优化算法的五次B样条轨迹规划方案，能够得到时间-脉动较优的轨迹，实现了六自由度机器人较高的运行效率和平稳性的研究目标。

[1] 蔡自兴.机器人学[M].北京:清华大学出版社,2000.

[2]JohnJ.Craig.机器人学导论[M].贠 超,等译.北京：机械工业出版社,2006.

[3]LinCS,ChangPR,LuhJYS.Formulationandoptimizationofcubicpolynomialjointtrajectoriesforindustrialrobots[J].IEEETransactionsonAutomaticControl, 1984, 28(12): 1066-1074.

[4]Planningofmanipulatormotiontrajectorywithhigher-degreepolynomialsuse[J].MechanismandMachineTheory.2008,44(7):1400-1419.

[5] 王幼民.机械臂关节空间B样条曲线轨迹规划[J].安徽机电学院学报,2000,15(2):21-26.

[6] 田西勇.机器人轨迹规划方法研究[D].北京:北京邮电大学,2008.

[7]ZhaXF.Optimalposetrajectoryplanningforrobotmanipulators[J].Mechanism&MachineTheory,2002,37(10):1063-1086.

[8] 徐海黎,解祥荣,庄 健,等.工业机器人的最优时间与最优能量轨迹规划[J]. 机械工程学报,2010,46(9):19-25.

[9] 杨国军,崔平远.机械手时间最优轨迹规划方法研究[J].中国机械工程,2002,13(20):1715-1717.

[10] 余 阳,林 明,林永才.基于混合遗传算法的工业机器人最优轨迹规划[J].计算机工程与设计,2012,33(4):1574-1580.

[11]GasparettoA,LanzuttiA,VidoniR,ZanottoV.Experimentalvalidationandcomparativeanalysisofoptimaltime-jerkalgorithmsfortrajectoryplanning[J].RoboticsandComputer-IntegratedManufacturing, 2012,28(2):164-181.

[12]GasparettoA,ZanottoV.Atechniquefortime-jerkoptimalplanningofrobottrajectories[J].RoboticsandComputer-IntegratedManufacturing, 2008,24(3):415-426.

[13]皮 格.非均匀有理B样条[M].北京：清华大学出版社,2010.

[14]潘 峰.粒子群优化算法与多目标优化[M]. 北京:北京理工大学出版社,2013.

[15]高卫峰,刘三阳.一种高效粒子群优化算法[J].控制与决策.2011,26(8):1158-1162.

Time-jerk Optimal Trajectory Planning for Industrial Robots Based on PSO Algorithm

Shen Yue，Li Yinya，Qi Guoqing，Sheng Andong

(School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)

In order to improve the work efficiency and guarantee the joints’ smooth movement of industrial robots, this paper proposes a scheme of time-jerk optimal trajectory planning based on PSO(particle swarm optimization) algorithm. First, the multi-objective optimization is transformed into single-objective optimization by the approach of weighting. Then, the time-jerk optimal trajectory is obtained by using PSO algorithm. And the trajectory planning is fulfilled in joint space coordinate by quintic non-uniform B-spline interpolation, and which can guarantee the jerk curves’ continuity. Finally, this scheme is applied to GRB4016—an industrial robot. The simulation results show that this scheme can generate ideal trajectory, and demonstrate the effectiveness of the proposed scheme.

B-spline curve; PSO; time-jerk optimal; trajectory planning

2016-07-19；

2016-08-17。

国家自然科学基金资助项目(61273076)。

沈 悦(1991-)，女，江苏南通人，硕士研究生，主要从事机器人方向的研究。

李银伢(1976-)，男，江苏南京人，副研究员，博士生导师，主要从事满意待机控制、非线性估计理论及其工程应用方向的研究。

1671-4598(2017)01-0158-05DOI：10.16526/j.cnki.11-4762/tp

TP

A