无人水下航行器势场航路规划方法研究

贾下跖, 刘可述, 张 孟, 邓 超

(1.山东核电有限公司，山东 烟台 264000；2.北京航天控制仪器研究所，北京 100854；3.东方电子股份有限公司，山东 烟台 264000)

无人水下航行器势场航路规划方法研究

贾下跖1, 刘可述2, 张 孟1, 邓 超3

(1.山东核电有限公司，山东 烟台 264000；2.北京航天控制仪器研究所，北京 100854；3.东方电子股份有限公司，山东 烟台 264000)

对运动障碍威胁环境下无人水下航行器(UUV)航路规划问题进行了研究;首先分别对规划过程中固定障碍、运动障碍建立了排斥势场，对目标点建立了吸引势场，将航路规划问题转变为寻找最优势场点问题；然后提出一种改进的粒子群算法(NPSO)，在UUV航路规划过程中，寻找距离当前路径点固定步长范围内的最优势场点，将其作为下一路径点，最终实现UUV在运动障碍威胁环境中的航路规划；最后对所提方法进行了仿真验证，UUV可以有效躲避固定障碍与运动障碍威胁，寻找到较优航路，取得了较好的仿真效果。

UUV；航路规划；势场；粒子群

0 引言

随着海洋经济的迅猛发展，无人水下航行器 (Unmanned underwater vehicle, UUV)也逐渐成为众多学者的研究热点，尤其是其在深海探测与开发、军事侦察与干扰等方面的应用越来越受到人们重视。在有海底山脉、沉船、礁岩等固定障碍物和舰艇等运动威胁的复杂海洋环境下，寻找一条能有效避开深海中各种固定障碍和运动威胁、顺利到达指定地完成勘测和侦察任务，无疑对无人水下航行器的航路规划技术提出了更高的要求[1]。

国内外众多学者通过对UUV航路规划问题的大量深入研究，提出了许多行之有效的航路规划算法[2-4]，诸如人工势场法、A-Star算法及其改进的D-Star算法、蚁群优化算法、神经网络算法等获得了广泛的研究与应用。但是，这些算法也具有其应用场合的局限性、算法的复杂性和搜索效率较低等问题。本文构建了一种UUV航路规划势场，并提出一种改进的粒子群算法，以提高粒子群算法的搜索性能，利用改进的粒子群算法寻找最优势场点，以实现复杂环境下UUV航路规划。

1 势场建立

本文针对固定障碍、运动障碍环境下的UUV航路规划问题进行研究。UUV规划起始点坐标为P0(x0,y0)，航路点坐标为Pi(xi,yi)，其中i=1,2,…n，终点坐标为Pg(xg,yg)。为简化问题，规划过程中，以固定步长S进行搜索。这样每一步搜索只需要寻找最优的前进角度ψ即可。

(1) 固定障碍势场。

如图1所示，为UUV躲避固定障碍航路规划示意图。

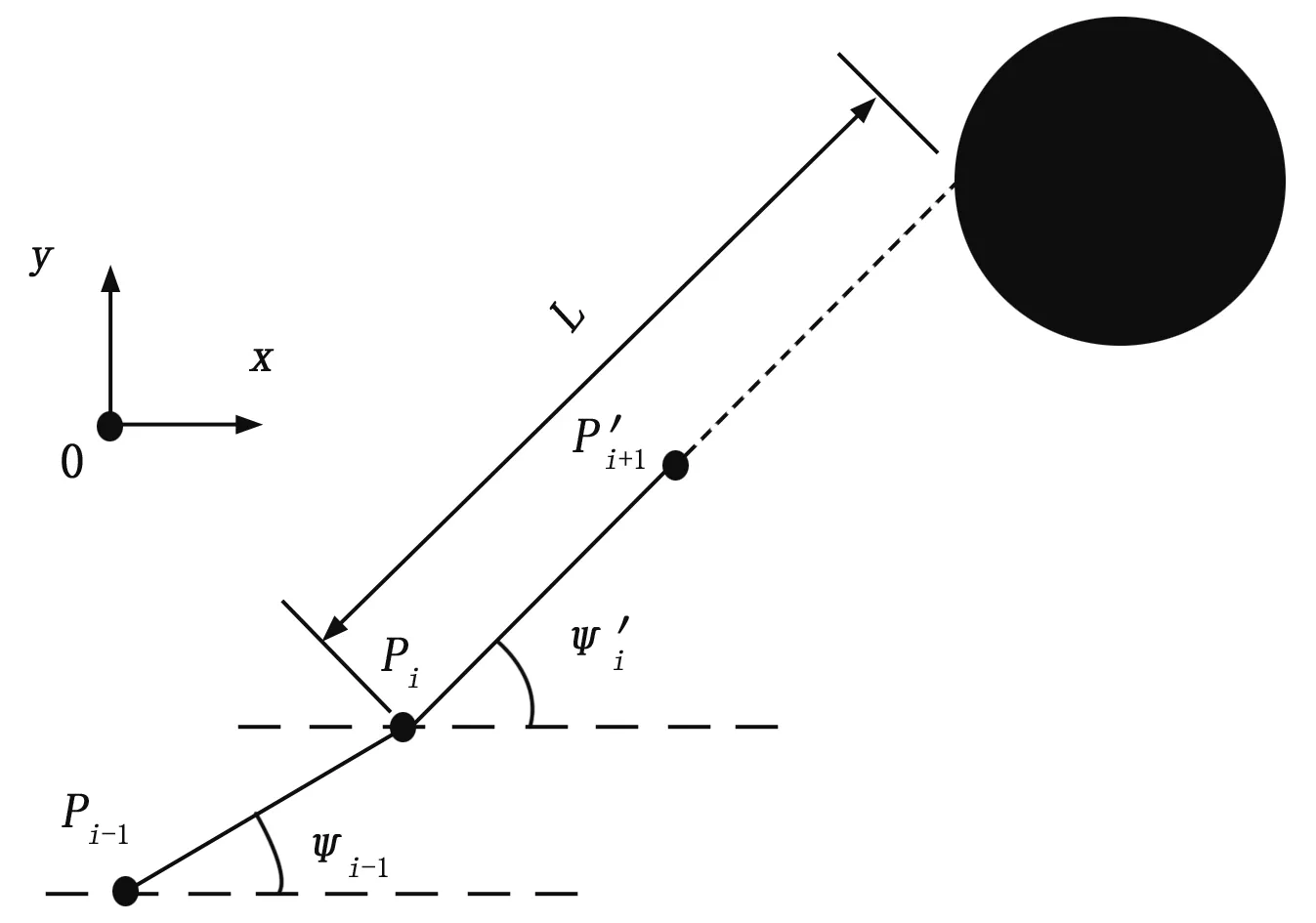
图1 UUV航路规划示意图

(1)

其中:S为UUV路径规划单步航行距离，UUV前行过程中始终寻找F1小的点，从而实现对固定障碍物的规避。

(2) 运动障碍势场。

UUV作业过程中会遇到舰艇等运动障碍。

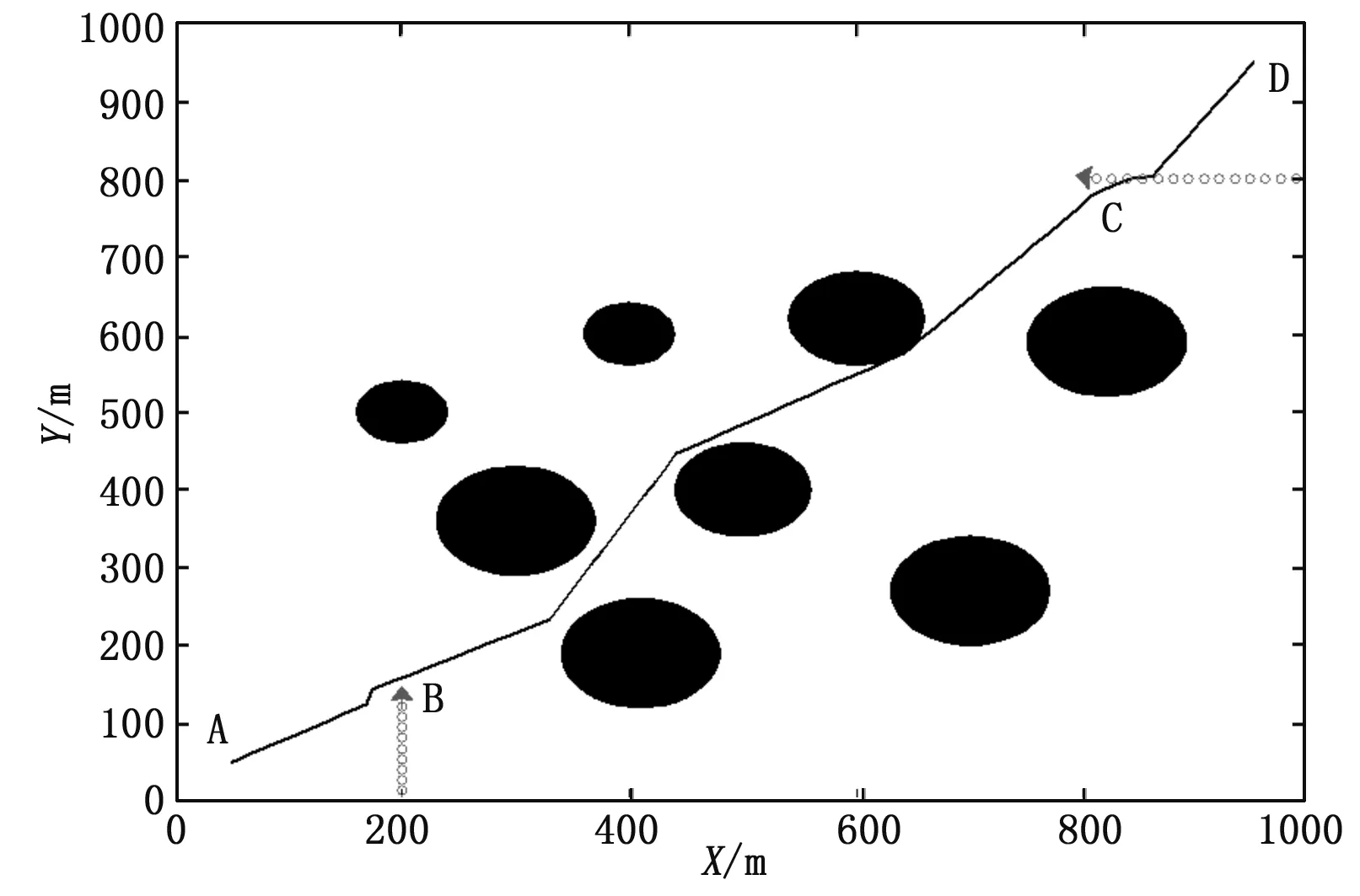
如图2所示，当前点Pi在候选点Pi+1方向延长线与运动障碍方向延长线的交点为M，UUV从Pi点运动到M点的时间为t1，运动障碍运动到M点的时间为t2。如果t2>t1则说明UUV先于运动障碍到达，t2-t1越大，UUV越安全，这里取函数e-β(t2 -t1 )2为运动障碍势场函数，当UUV距离交点越近时避碰行为越强，UUV距离交点越远时避碰行为越弱，因此运动障碍势场函数调整为：e-αt12*e-β(t2 -t1 )2。如果t2

图2 UUV运动障碍规划示意图

(2)

如果交点M不存在，则说明UUV与运动障碍运动航线不相交，此时同样有F2=0。

(3) 吸引势场。

为实现UUV朝向目标运动，需要建立吸引势场。如图3所示。

图3 吸引势场示意图

(3)

(4)UUV航路规划总势场函数。

UUV航路规划总势场函数为各势场函数的叠加。从而有：

F=k1F1+k2F2-k3F3

(4)

其中:ki为权重系数(ki>0)。

基于上述分析，建立了当前航迹点的UUV航路规划势场函数后，利用粒子群算法搜索使势场函数获得最小值的航迹点，将该搜索到的航迹点作为UUV航行路径中下一时刻的航迹点，依次原理逐步获得一系列的航迹点，最终得到优化航行路径，实现航路规划。

2 改进粒子群算法

粒子群算法(particle swarm optimization)也称粒子群优化算法，具有参数调节简单，易于实现，精度高、寻优能力强等优点[5-7]。因此该算法一经提出便引起许多专家学者的重视，演化出诸多改进策略，提高算法性能[8-11]。自身历史最优位置、自身惯性速度、群体历史最优位置是粒子群优化算法中影响其搜索性能的3个主要因素。本文针对这三大主要因素，提出了一种有利于提高算法性能的改进粒子群优化算法(novel particle swarm optimization, NPSO)。在粒子群优化算法搜索过程中，每一个粒子分别朝下列3个不同方向进行进化：自身最优位置、种群最优位置、自身最优与种群最优的加权位置，继而产生3个同源的子粒子，然后比较这3个同源子粒子适应度，根据优胜劣汰的原则，保留适应度最优的子粒子。即有粒子进化方程：

(5)

从而：

(6)

变量定义：

rt,t=1,2,3：取值介于[0,1]之间的随机数；

ω：粒子进化产生子粒子的速度方向惯性权重；

ci(i=1,2)：学习因子；

pgd(k)：第k次迭代后种群最优粒子第d维坐标。

3 算法性能分析

3.1 算法收敛性分析

对于进化方程：

(7)

(8)

当c1r2=0、c2r3=0、ωr1=0时分别对应NPSO的3个不同进化方向，显然NPSO是进化方程(7)、(8)的特殊进化方式，如果进化方程(7)、(8)收敛则NPSO收敛。

(9)

(10)

其中：φ1=c1r2，φ2=c2r3，φ=φ1+φ2，φp=φ1pid(k)+φ2pgd(k)。

定义：

从而有：

(11)

当矩阵的特征根具有负实部时，方程(11)收敛，有特征方程：

(12)

解得特征根为：

(13)

从而只需ωr1-φ-1<0，即可保证进化方程(7)、(8)收敛，进而保证NPSO收敛。

3.2 算法搜索性能分析

为衡量算法的搜索性能，采用不同的测试函数对算法进行测试，并将NPSO与(Basicparticleswarmoptimization)BPSO、(Linearlyvaryinginertiaweight)LWPSO、(Exponentialinertiaweightstrategies)EPSO、(Time-varyingaccelerationco-efficient)TVAC性能进行比较[8-11]。

采用的测试函数为：

(1)sphere函数：

(2)Rotatedhyper-ellipsoid函数：

(3)Rosenbrock函数：

-100

(4)Rastrigin函数：

(5)Griewank函数：

Kennedy研究认为c1、之和取4.0时，可以获得较好的搜索效果[12]，一般把它们均设为2。

为了获得较好的搜索效果，通常取惯性权重ω为0.7、种群数量为30[12-13]。在仿真中，对BPSO、LWPSO、EPSO、TVAC优化算法，种群粒子个数选为n=30，而对于NPSO，因为其在进化过程中产生3个子粒子，所以选取n=10。在对比各算法搜索性能测试的仿真实验中，各相关参数的取值如表1所示。

如果粒子位置为搜索过程中超出搜索空间，则将粒子位置坐标设为此时的边界坐标、粒子速度设为零；同理，如果粒子速度超出速度边界，则将此时粒子速度设为速度边界值。为了让仿真实验结果更加准确可靠，对每个测试函数的优化过程都重复100次，并对这100次测试结果求取平均值和标准差。仿真实验结果如表2所示。

表1 不同优化算法相关参数取值

表2 BPSO、LWPSO、EPSO、TVAC和NPSO对比结果

注：表中数据为均值±标准差

图4 平均适应度变化曲线图

由表2可以看出，对于单模态测试函数，上述各种搜索算法的搜索精度和稳定性由高到低依次为NPSO、TVAC、EPSO、LWPSO、BPSO；但是NPSO唯独对高度多模态Rastrigin函数搜索效果不太理想。

图4所示为不同搜索算法在Rosenbrock函数f3和Griewank函数f5进化过程中的平均适应度变化曲线。从该图中可以清晰的看出，各算法的收敛速度由快到慢依次为NPSO、TVAC、BPSO、EPSO、LWPSO。

本文验证了各算法在不同自变量维数D下的搜索性能：自变量维数D从10增加到100的过程中，求取不同算法下测试结果的平均值和标准差。表3所示为Rosenbrock函数f3在自变量维数D由10增加到100的部分实验数据。由表3可以得知，各算法的搜索精度和稳定性均会随着测试函数维数的增加而出现不同程度的降低，但TVAC和NPSO算法的搜索精度和稳定性要优于其他算法。

表3 Rosenbrock函数不同维数下BPSO、LWPSO、EPSO、

注：表中数据为均值±标准差

4 UUV航路规划仿真

利用所提算法对UUV在动态障碍环境中的航路规划进行仿真，由UUV当前点出发，以固定步长前行，在UUV最大转角约束范围内，利用改进的粒子群算法寻找具有最优势场点的候选点，作为UUV前进的下一路径点，逐步完成UUV航路规划。仿真环境为1 km×1 km的区域，UUV起始点为A(50,50)，目标点为G(950,950)。ki=1,i=1,2,…,4，σ=2。仿真步长为20m，为简化问题，仿真时UUV以4m/s的速度匀速前进，分别遭遇横坐标为200m平行于y轴的运动障碍B，与纵坐标为800 m，平行于x轴的运动障碍C。

图5 运动障碍环境下UUV航路规划效果图

从仿真图5上可以看出，UUV遭遇运动障碍B时，选择从运动障碍B之前绕行，遭遇运动障碍C时，选择从运动障碍C之后绕行，本文所提方法能有效的避开威胁域。仿真结果表明本文所提方法可以有效实现UUV运动障碍环境下的航路规划，获得了较好的规划效果。

为进一步检验本文所提算法性能，对复杂环境下的UUV航路规划进行了仿真验证，并与传统人工势场算法进行比较，仿真结果如图6所示。

图6 复杂环境下UUV航路规划

图6中实线为本文所提算法规划的UUV航路，黑色点划线为传统人工势场算法规划的UUV航路。为对比复杂环境下算法有效性，仿真时UUV起始点设为A(50,50),目标点设为B(950,950)，从图6可以看出，本文所提算法在复杂的环境中可获得较优的UUV规划航路，而传统人工势场算法容易陷入障碍区域无法实现航路规划。为对比本文所提算法与传统人工势场算法所搜索路径的优化性，UUV起始点设为C(50,950)，目标点设为D(950,50)，仿真结果显示，本文所提算法规划路径长度为1 308 m，传统人工势场算法规划路径长度为1 504 m。由仿真图6可以看出，传统人工势场算法在障碍物前容易震荡，陷入不稳定运动状态，本文所提算法可以获得较优的平滑路径，明显优于传统人工势场算法。

5 结论

本文首先分别对固定障碍和运动障碍威胁环境建立了排斥势场，对目标点建立了吸引势场，将航路规划问题转变为寻找最优势场点问题；然后提出了NPSO算法，并应用典型评价的函数对算法性能进行了分析；最后将所提出的NPSO算法应用到运动障碍威胁环境下UUV航路规划问题中，通过分析仿真结果可得出以下结论：

(1) NPSO算法通过在每次粒子进化过程中，向3个不同方向搜索，使得搜索更充分，并对子粒子优胜劣汰得到最终的搜索结果，有利于寻找到较快的收敛方向。对典型评价函数的仿真结果表明，对于单模态函数，NPSO在搜索精度和收敛速度上均优于BPSO、LWPSO、EPSO以及TVAC。但是，对高度多模态函数NPSO搜索效果并不十分理想，这是由于NPSO算法相对于其它算法每次迭代更容易找到收敛较快的搜索方向，使得NPSO算法过快收敛而多样性有所降低。

(2) 本文所设计的航路规划方法通过建立运动障碍遭遇时间模型，得到躲避运动障碍势场函数，利用粒子群算法寻找势场值最小点，从而在运动障碍威胁环境中，能有效的避开障碍物，获得较优的规划航路，效果良好。

(3) 对复杂环境下UUV航路规划的仿真显示，相对于传统人工势场，本文所提算法可以得到较优的规划航路，且不容易陷入局部极小点，可实现复杂环境下的航路规划，然而要实现彻底避免陷入局部极小点，或U型障碍，还需要进行UUV状态判断与逃逸规则的设计，这是后续工作需要加强和完善的地方。

[1] Liu Liqiang, Dai Yuntao. 3D Space Path Planning of Complex Environmental Underwater Vehicle[A].2009 International Joint Conference on Computational Sciences and Optimization[C]. 2009: 204-209.

[2] Zhang J J. Research on Autonomous Navigation Planning of Underwater Vehicle Based on Genetic Algorithm[D]. Harbin: Harbin Engineering University, 2003.

[3] Nathan E B. Three-Dimensional Route Planner Using A* Algorithm Application to Autonomous Underwater Vehicles[R]. Louisiana State University Report, 2008.

[4] 朱 毅，张 涛，宋靖雁.非完整移动机器人的人工势场法路径规划[J].控制理论与应用，2010, 24(2): 154-161.

[5] Mondal D，Chakrabarti A, Sengupta A. Optimal placement and parameter setting of SVC and TCSC using PSO to mitigate small signal stability problem[J]. Electrical Power & Energy Systems, 2012,42(1): 334-340.

[6] Ishaque K，Salam Z, Amjad M, et al.An Improved Particle Swarm Optimization (PSO)-Based MPPT for PV With Reduced Steady-State Oscillation[J]. Power Electronics, IEEE Transactions on, 2012,27(8): 3627-3638.

[7] Mohammadi-Ivatloo B, Rabiee A, Soroudi A, et al.Iteration PSO with time varying acceleration coefficients for solving non-convex economic dispatch problems[J]. Electrical Power & Energy Systems, 2012, 42(1): 508-516.

[8] 张顶学,关治洪,刘新芝.一种动态改变惯性权重的自适应粒子群算法[J].控制与决策，2008,23(11):1253-1257.

[9] Sdsngs, Ratnaweera, Saman K. Halgamuge, Harry C. Watson. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients[J]. IEEE Transaction on evolutionary computation 3(8):240-255.

[10] Shi Y, Eberhart R. A modified particle swarm optimizer[A].IEEE World Conf on Computational Intelligence[C]. Piscataway: IEEE Press,1998: 69-73.

[11] Chen G M, Huang X B, Jia J Y, et al. Natural exponential inertia weight strategy in particle swarm optimization[A]. Proc of 6th Congress on Intelligent Control and Automation[C]. Dalian: IEEE Press, 2006:3672-3675.

[12] Kennedy, J. (1998). The behavior of particles[A]. 7thAnnual Conference on evolutionary programming[C]. San Diego, USA.

[13] Shi Y, Eberhart R C. Empirical Study of particle swarm optimization[A]. 1999 congress on evolutionary computing[C]. Vol. III, pp 1945-1950.

[14] Carlisle A, Dozier G. An Off-The-Shelf PSO[A]. Proceeding of the 2001 Workshop on Particle Swarm Optimization[C].1-6.

Potential Field Method for Unmanned Underwater Vehicle Path-planning

Jia Xiazhi1, Liu Keshu2, Zhang Meng1, Deng Chao3

(1.ShanDong Nuclear Power Company LTD, Yantai 264000, China; 2.Beijing Aerospace Control Instrument Research Institute, Beijing 100854, China; 3.Dong Fang Electronics Co.,Ltd., Yantai 264000, China)

The problem of UUV path-planning under the environment of movement disorders has been addressed. Firstly, potential field method is proposed to build rejection potential field for fixed obstacles and movement disorders, and attractive potential for objective point. Then, a novel particle swarm optimization (NPSO) is proposed and applied to find the optimal potential field point as the next path point, which point of fixed step length distance from the current point, so as to realize UUV path-planning under movement disorders threat. Finally, simulation is presented, demonstrating that UUV can dodge obstacles and threat, and search for the better sea-lane.

UUV; path-planning; field; PSO

2016-07-15；

2016-09-13。

贾下跖(1988-)，女，湖北天门人，主要从事核电站仪控仪表方向的研究。

1671-4598(2017)01-0144-05

10.16526/j.cnki.11-4762/tp.2017.01.041

TP301.6；TP18

A