一类含饱和项和毒素项的扩散问题的周期解

冯庆红

(常州工学院数理与化工学院，江苏 常州 213032)

0 引言

生态环境中广泛存在着互惠关系。随着偏微分方程理论的发展，数学生态学中大量带饱和项和扩散项的互惠模型被建立并得到研究[1]。长期以来，种群在毒素环境中持续生存的状况一直受到广泛的关注[2]。学者们对扩散问题周期解的存在性的研究已经取得了丰富成果[3-4]。文献[5]运用时标上连续及拓扑度定理研究了一类种群捕食模型，得到了模型存在周期解的充分条件。文献[6]利用比较原理讨论了系统的持久性、正平衡点的局部稳定性以及全局稳定性，但由于系统是用常微分方程表示的，并没有涉及周期解的研究。在此基础上，本文考虑以下具有周期系数和Neumann边界的空间扩散互惠模型：

(1)

1 一般问题周期解的存在性

为了讨论问题(1)的周期解的存在性，我们先讨论一般的具有周期条件的抛物边界问题。

(2)

其中：i=1,2,…,N；Ω是Rn中的有界区域, 边界∂Ω光滑，

u≡u(x,t)≡(u1(x,t),u2(x,t),…，uN(x,t))。

对于i=1,2,…,N,有：

本节假设下面的条件成立：

(H2)fi(·,u)关于变量u满足局部的Lipschitz条件, 即

|fi(·,u)-fi(·,v)|≤Ki(|u-v|),∀i=1,…,N,u,v∈S,

其中：Ki为Lipschitz常数；S为选择的上下解的范围(见式(3))。

定义：存在向量函数

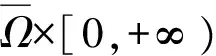
其中：

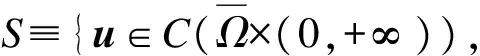
(3)

注：由以上耦合上下解的定义可知，不需要限定上下解为时间t的T周期函数。

2 问题(1)周期解的存在性

下面的定理给出了T周期解存在的结论，其证明见文献[7]第428页推论 2.1。

下面我们讨论问题(1)周期解的存在性，首先假设

(G)a(t),b(t),c(t),d(t);ri(t),ai(t),γi(t)(i=1,2)均为关于t的严格正的有界Hölder连续函数且为周期T函数。

为了方便讨论，这里用g(t)表示上述的连续且有界函数，记

实际问题中，一些两种或两种以上种群系统中反应函数f(·,u)=(f1(·,u),f2(·,u)，…,fN(·,u))具有拟单调性。

记

u≡(ui,[u]ai,[u]bi),

其中[u]σ定义u中指标为σ的向量，如果对于任意的i=1,2，…,N，存在非负整数ai,bi且ai+bi=N-1时函数fi(·,ui,[u]ai,[u]bi)对于[u]ai非减,对于[u]bi非增,此时称f(·,u)=(f1(·,u),f2(·,u)，…,fN(·,u))具有混合拟单调性质。特别地，如果对所有i，bi=0,则称f(·,u)=(f1(·,u),f2(·,u)，…,fN(·,u))是拟单调非减的。

易知，互惠模型方程右端函数是拟单调非减的。

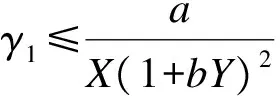
(4)

(5)

则化为了拟单调非减问题,其中，MX,MY为关于X,Y的待定常数。

下面利用上下解方法讨论拟单调非减化后的问题(1)的周期解的存在性。构造如下形式的上下解

显然，由上面讨论可知，在条件(4)和(5)下，问题(1)描述的是互惠系统，故上下解是有序的，它们满足

MX≥δ,MY≥δ,

且

(6)

(7)

(8)

(9)

取

类似地，取

综上所述，(MX,MY)和(δ,δ)是周期问题(1)的有序上下解。 同时，由文中给出的周期解存在定理可知，问题(1)至少有一个周期解。

3 结语

文章为了讨论周期系数偏微分问题 (1) 周期解的存在性，先研究了一个一般的具有周期条件的抛物边界问题 (2)。假定一般问题满足一定条件，在给出耦合上下解的定义之后，利用周期解存在定理，证明了如果一般问题存在一对耦合上下解，它就至少存在一个T周期解的结论。经过计算寻找到使问题(1)拟单调非减的条件后，利用上下解的方法，得到了问题(1)存在一个周期解的结论。研究表明，随时间的增大，问题 (1)中种群密度将呈现周期振荡状态。

[1]KIM K I,LIN Z G.Blow-up in a three-species cooperating model[J].Appl Math Lett,2004,17(1):89-94.

[2]朱晶.有毒物影响和Bedding-DeAngelis型功能性反应的捕食系统的全局吸引性[J].生物数学学报，2013,28(4):716-724.

[3]张金陵.一类具有Holling-Ⅱ型功能函数的捕食模型周期解的存在性[J].聊城大学学报(自然科学版)，2012,25(4):18-22.

[4]徐海娜,林支桂.一类互惠生态模型解的周期性和爆破[J].生物数学学报，2011,26(4):734-742.

[5]徐昌进.时标上具有阶段结构的三种群捕食系统的周期解[J].经济数学学报，2013,30(1):5-11.

[6]向红，苏克所，姜惠敏，等.具有饱和项和毒素影响的互惠模型的定性分析[J].兰州交通大学学报，2010,29(3):142-145.

[7]PAO C V.Stability and attractivity of periodic solutions of parabolic systems with time delay[J].J Math Anal Appl,2005,304(2):423-450.