GNSS载波相位测量── GNSS卫星导航定位方法之六

刘基余

（武汉大学测绘学院，武汉 430079）

GNSS载波相位测量── GNSS卫星导航定位方法之六

刘基余

（武汉大学测绘学院，武汉 430079）

GNSS载波相位测量，不仅能够用于毫米级精度的静态定位，而且能够用于厘米级精度的动态定位，本文以GPS信号为例，论述了几种测量载波相位的实用方法。

GNSS信号；载波相位；GPS信号接收机

GPS卫星测量技术问世之初，人们认为只能依靠P码才能达到较高的动态定位精度。然而，P码是美国国防部控制的保密军用码，它不仅是具有2.35E+14个码元的长伪噪声码，而且在SA影响下译密成更难破译的Y码。对于非特许用户而言，探求精密定位方法，是开发和应用GPS动态测量技术的重大课题。GPS静态定位已经成功地采用了载波相位测量方法，取得了三、五千千米长基线达到±(5mm+0.01PPM)的测量精度，且其三维位置误差仅为±3cm。因为，载波波长较P码码元的相应长度短两个数量级；在相位测量精度相同的情况下，载波相位测量误差对测距精度的损失，较P码码相位测量误差小两个数量级。不仅如此，载波相位测量的距离分辨率也较P码码相位测量的距离分辨率高得多；例如，TI-4100 GPS信号接收机具有2-16的分辨率，这对用P码码相位测量而言，其距离分辨率可达0.447mm，对载波相位测量(L1)而言，则可达到0.0029mm的距离分辨率。因此，GNSS载波相位测量已经成为高精度定位的主要方法。

现以GPS为例，如果忽略某些附加滞后相位，GPS信号接收机所接收到的GPS信号可表述为

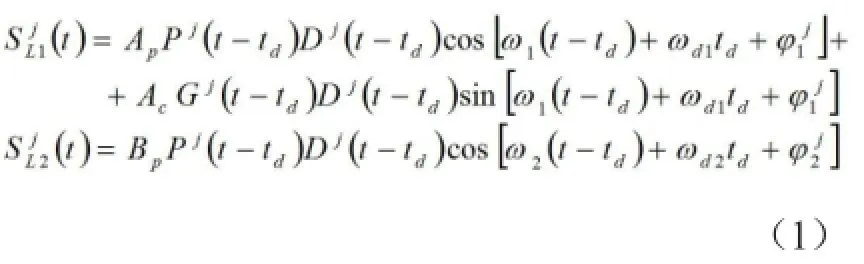
式中，Ap，Ac，Bp分别为1575.42MHz载波L1和1227.60MHz载波L2的振幅；Pj(t-td)为第j颗GPS卫星的P码；Gj(t-td)为第j颗GPS卫星的C/A码；Dj(t-td)为第j颗GPS卫星的D码，即卫星导航电文；td为GPS信号从第j颗GPS卫星到达GPS信号接收天线的传播时间，其大小正比于站星瞬时距离的长短；ω1为第一载波L1的角频率；ω2为第二载波L2的角频率；为第j颗GPS卫星载波L1的初相；为第j颗GPS卫星载波L2的初相；为第j颗GPS卫星载波L1的多普勒角频率；为第j颗GPS卫星载波L2的多普勒角频率。

从式（1）可见，第j颗GPS卫星发送的导航定位信号，既可以用其伪噪声码测量站星距离，又可以通过测量载波在用户和GPS卫星的滞后相位，而间接地测得同一站星距离，依此而解算出用户的实时位置。但是，GPS载波相位测量，较伪噪声码的伪距测量要复杂一些。现对载波相位测量的相关问题予以简要论述。

1 多普勒频移测量

GNSS卫星环绕地球而不断飞行，GNSS用户与GNSS卫星之间存在着相对运动，以致GNSS信号接收天线所接收到的GNSS卫星发射的载波频率（fS），附加着多普勒（Christian Doppler）频移。依图1而知

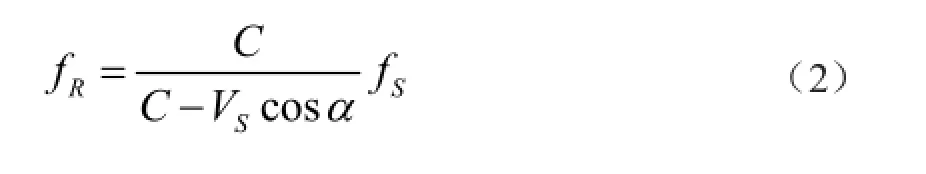
式中，fS为GPS卫星发射的载波频率（简称为发射载频）；fR为到达GNSS信号接收天线的GPS卫星的载波频率（简称为接收载频）；VS为GNSS卫星的切向（顺轨）速度；C为GNSS信号传播速度；α为用户至GNSS卫星的矢径与其切向速矢的夹角。

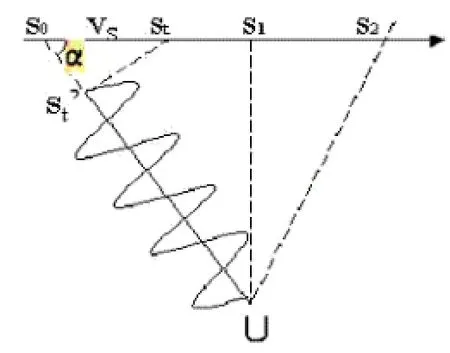
图1 多普勒频移的导出

从式（2）可见，当GNSS卫星的切向速度为零时，接收载频等于发射载频，即，当GNSS卫星处于用户天顶时，多普勒频移为零；且知，多普勒频移相应于站星距离（ρ）的变化率。考虑到C>>VS，以及dρ/dt=VScosα，则式（2）可写成

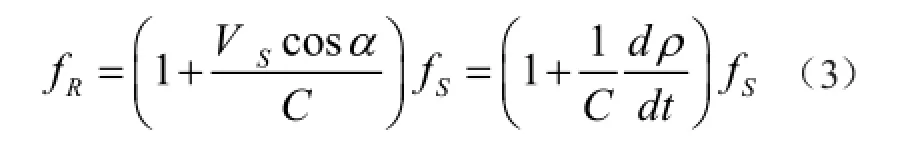
故知多普勒频移为

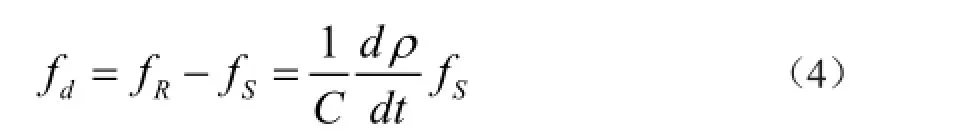
为了提高多普勒频移的测量精度，一般不是直接测量某一时元的多普勒频移，而是测量在某一时间间隔（t1，t2）内的多普勒频移之积累数值，称之为多普勒计数（Cd），即

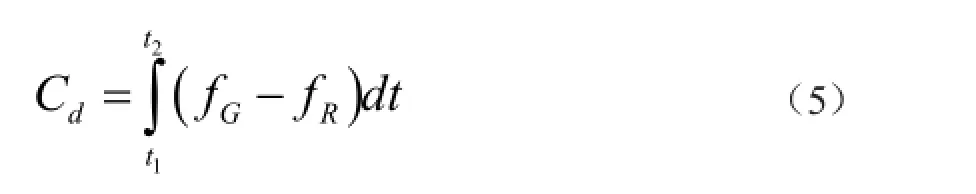
式中，fG为GNSS信号接收机所产生的载波频率；fR为GNSS信号接收机所接收到的载波频率。

考虑到f=dφ/dt，多普勒计数可以改写为

式中，φR为GNSS信号接收机所接收到的载波相位；φG为GNSS信号接收机所产生的载波相位。

同理，GPS信号接收机，可以通过测量载波相位变化率而测定GPS信号的多普勒频移，其相应的距离变率测量精度，在2000年5月1日以前有SA技术的作用下，且用DGPS测量模式，可达2mm/s～5cm/s。对于一个静态用户而言，GPS多普勒频移的最大值约为±4.5kHz。如果知道用户的概略位置和在视卫星的历书，便可估算出GPS多普勒频移，而实现对GPS信号的快速捕获和跟踪；这很有利于GPS动态载波相位测量的实施。

2 波数和整周跳变

在作动态载波相位测量时，GNSS信号接收机既要接收和解释出来自GNSS卫星的载波信号，又要产生一个与接收载波频率相同的载波信号；前者叫做被测载波，后者叫做基准载波。载波相位测量值，是基准载波相位和被测载波相位之差，即

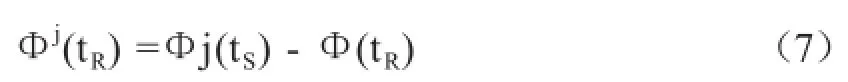
式中，Φj(tS)为第j颗GNSS卫星在时元tS发射的载波相位；Φ(tR)为GNSS信号接收机在时元tR所产生的基准载波相位。

为了解算动态用户的三维位置，GNSS信号接收机需要观测四颗以上的GNSS卫星；各颗GNSS卫星在不同的时元向GNSS用户发送频率相同的载波信号，而存在发射时元和接收时元的归一化问题。现将发射时元表述为接收时元的函数，即

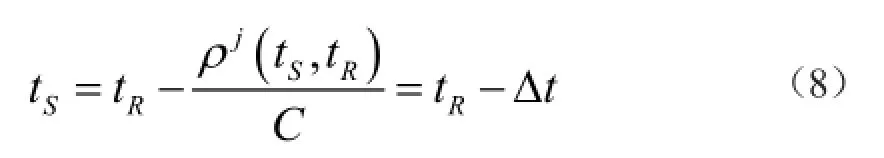
式中，ρj(tS, tR)为第j颗GNSS卫星在时元tS发射的载波信号，而于时元tR到达GNSS信号接收天线所经过的距离，即站星距离；C为GNSS信号的传播速度。

考虑到式（8），则式（7）可写作为

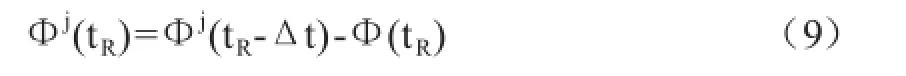
从GNSS卫星至用户的距离可知，Δt ≈ 0.067s，故有

式中，dΦj/dt是第j颗GNSS卫星的载波频率（f）；考虑到Δt = ρj(tS, tR)/C和式（10），则依式（9）可知，以周为单位的载波相位测量值是

式（11）是归化为GNSS信号接收机时系的载波相位测量值；实际上，GNSS测量数据处理，均采用GNSS时间系统。而归化到GNSS时系的载波相位测量值为

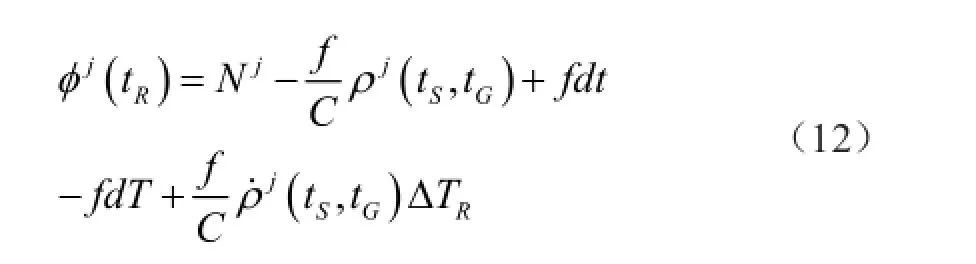
式中，Nj为第j颗GNSS卫星发射载波至GNSS信号接收机的滞后相位波数，也称之为整周模糊度或整周待定值（如图2所示）；dt为第j颗GNSS卫星时钟相对于GNSS时系的偏差；dT为GNSS信号接收机时钟相对于GNSS时系的偏差；ΔTR为站星距离变率的时间间隔；为站星距离变化率。

当用GPS第一载波测量时，其载频fL1=1575.42MHz，它的相应波长λ=19cm，用该电尺量测二万余千米的GPS站星距离，其整尺段数（波数）约为1E+8。如此巨大的波数（如表1所示），是无法直接精确测定的，而需用一定的方法求解这个未知数。因此，波数（整周模糊度）的解算，是载波相位测量数据处理的一个特殊而又极重要的问题。

图2 GNSS动态载波相位测量

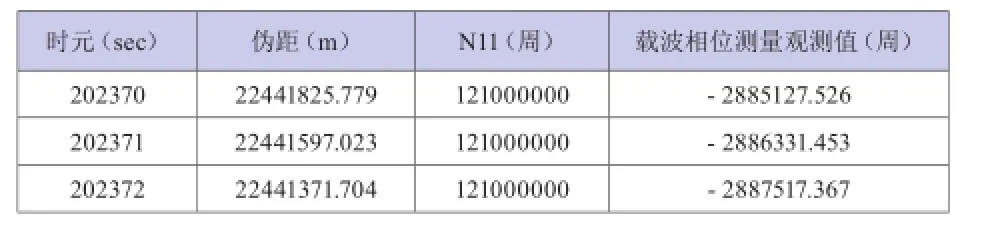
表1 波数解算之例

若考虑到波长λ=C/f，由式（12）可知，以米为单位而在时元t测得的载波相位是

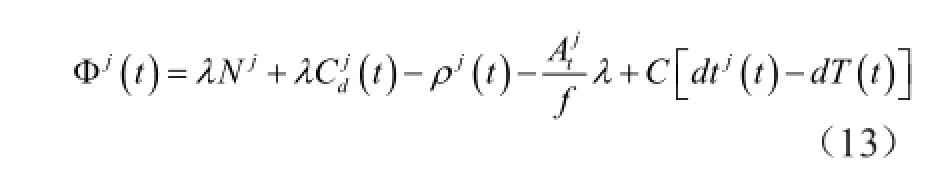
式（13）中的波数Nj是基于下述实事而成立的：从初始时元t0到观测时元t，计数器始终处于连续不断的计数状态，以致在[t0t]时域内多普勒计数是连续的，以此确保观测时元t的波数等于初始时元t0的波数；即，在[t0t]时域内只有一个波数Nj。

但是，用于测量载波滞后相位的锁相环路，在强干扰信号的作用下，它的稳定平衡状态受到了破坏，以致环路鉴相器的工作点跳过2π，甚至若干个2π；随着干扰信号减弱到阈值以下，致使锁相环路趋向新的稳定平衡状态，而恢复正常的测相作业；跳越2π的数目，既取决于干扰信号的强度，又取决于干扰信号的持续时间。GNSS信号接收机锁相环路稳定平衡状态的破坏，导致了多普勒计数的记录中继，这种丢失多普勒计数的现象，叫作整周跳变（cycle slip），简称为周跳。

从式（13）可见，若在时元t1发生了周跳，而于时元t3恢复多普勒计数；时元t3的波数Nj(t3)=Nj+ΔNj；即，时元t3的载波相位测量增加了一个新的未知数ΔNj。为了在第j颗GNSS卫星一次通过中，将波数Nj作为同一个未知数进行整体解算，需要用一定的方法强迫周跳前后的波数相同，而进行周跳的探测和修复。这是确保高精度定位连续稳定的关键问题。

3 载波相位的跟踪与测量

现代的数字式GPS信号接收机，包括如图3所示的主要部件；该图所示的信号处理器，是由伪噪声码延时锁定环路（DLL）和载波相位锁定环路（PLL）构成的，而能够测定出伪噪声码所历的伪距（P）和载波从GPS卫星至GPS信号接收天线的滞后相位（Φ）。

当只考虑C/A码及其载波时，所考虑的GPS第一导航定位信号依式（1）而知：

图3 GPS信号接收机的基本结构

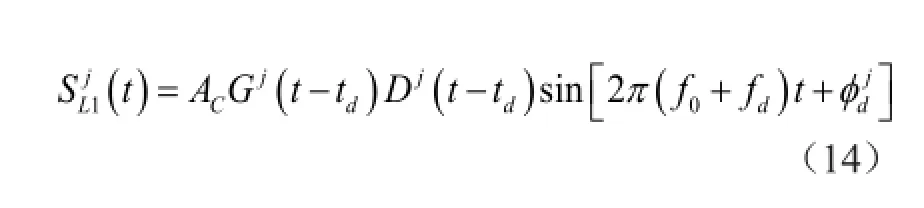
式中，f0=fL1-fL0，此处，fL0为本振频率，对于NovAtel接收机而言，f0=35MHz；φjd=-ω1td+，它主要是载波从GPS卫星至GPS信号接收天线的滞后相位；fd为多普勒频率。

经过IF采样和A/D变换器的作用，式（14）所表述的GPS信号，被分解为同相分量和正交分量，且知

上述分量同时送入信号处理器，用以测得伪距和载波滞后相位，此处仅讨论载波相位的测量。

3.1 载波锁相测量法

GPS载波相位测量，是基于伪噪声码的锁定成功，即，延时锁定环路（DLL）对信号分量和的多次互相关运算结果，致使接收C/A码和本地C/A码严格“对齐”，而获得最大的互相系数（1），从而锁定住第j颗GPS卫星的C/A码；此时，方可按如图4所示的载波相位锁定环路（PLL）测量出载波滞后相位。

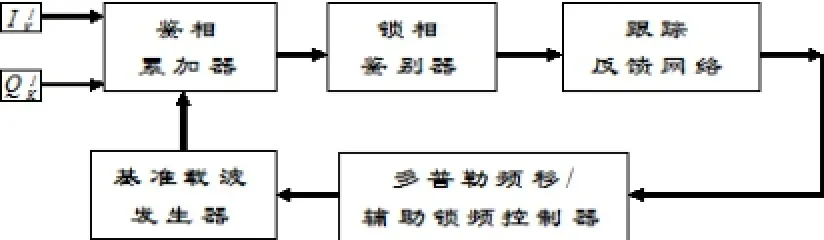
图4 载波锁相测量方框图

若考虑到A/D变换器的采样时区tK，则式（15）的数字化信号形式为

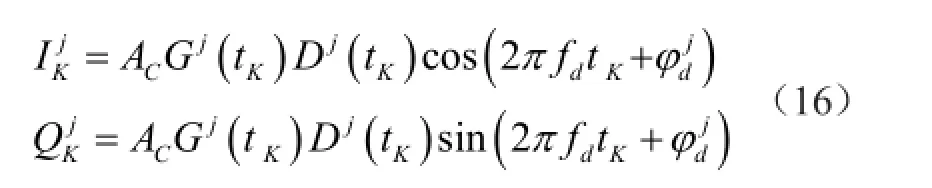
在图4的鉴相累加器中，式（16）的两个数字化信号与来自基准载波发生器的相应数字化信号，实施鉴相运算而形成新的同相分量I和正交分量Q，即，

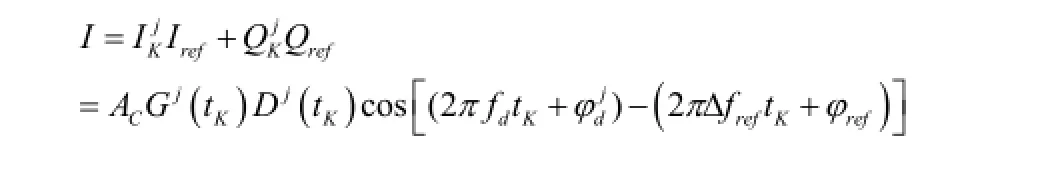
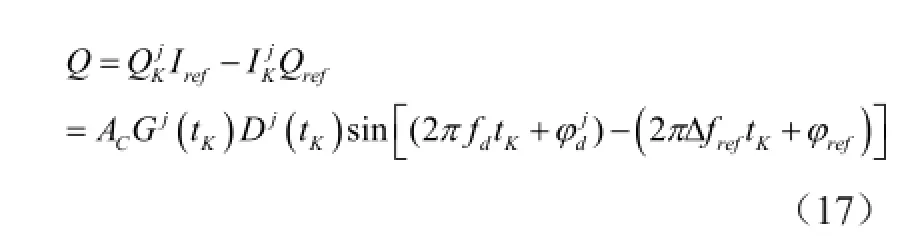
式中，Iref和Qref为基准载波的同相分量和正交分量；Δfref为基准载波的频率相对于被测载频fL1的频偏；φref为基准载波的初相。

锁相鉴别器对式（17）两个信号分量的相位差进行鉴别，而判别ΔΦ（=IQ）是否等于零；若ΔΦ≠0，则输出一个误差电压U(ΔΦ)，经过具有1Hz带宽滤波器的跟踪反馈网络而馈送到多普勒频移/辅助锁频控制器，用以实现对基准载波频率的不断调控，一直调控到ΔΦ=0为止。此时则有

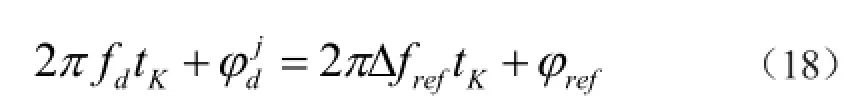
这表明GPS信号的载波已经被锁定住，而能够测得GPS信号载波的滞后相位。顺便指出，载波相位锁定环路，对信号相位噪声非常敏感；加拿大学者R. B. Langley的研究表明，载波相位锁定环路的噪声相位测量偏差（ΔΦPLL），可近似表述为：

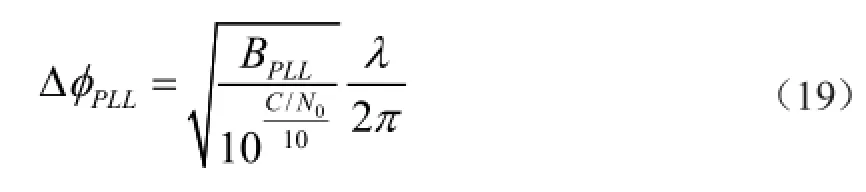
式中，BPLL为载波相位锁定环路噪声频带宽度（Hz）；C/N0为载波/噪声功率密度比（dB-Hz）；λ为载波的波长。

从式（19）可知，若取C/N0=45dB-Hz，BPLL=2Hz，对于第一载波(L1)而言，ΔΦPLL=0.30mm；若其它条件不变化，仅改变C/N0=25dB-Hz，则ΔΦPLL=3.04mm。因此，为了获取高精度的载波相位测量值，GPS信号接收机的制造者，应特别注重基准载波发生器的高稳定度；GPS信号接收机的使用者，应特别注重基准载波发生器的维护。

3.2 平方律测量法

为了简明起见，在论述GPS载波相位的平方律测量法时，暂不考虑GPS信号的频率变换，即，图5的输入信号为

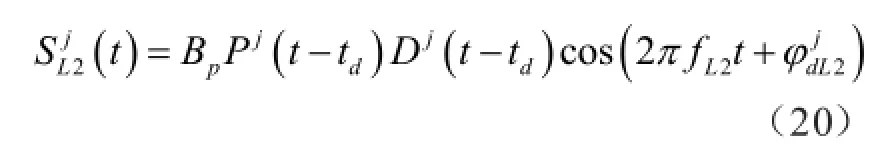
上述信号分两路送入混频器，用其非线性特性的和频项，即，信号在混频器中自乘而得

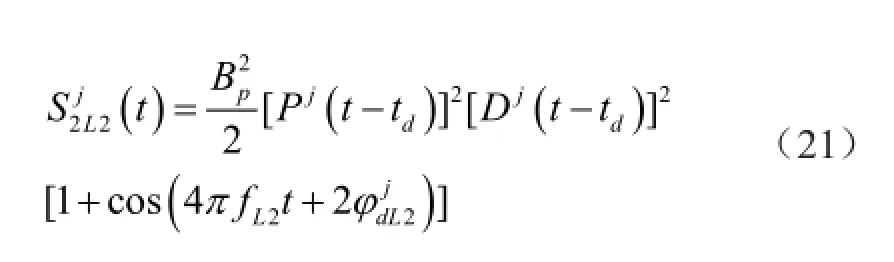
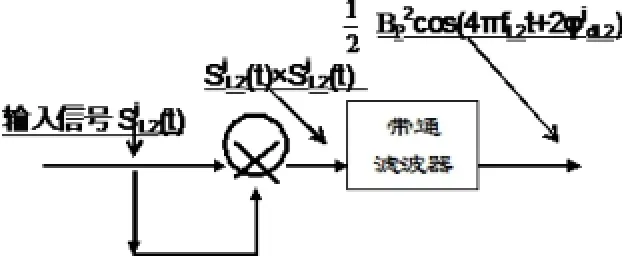
图5 平方律测量法图示意图

因Pj和Dj均为取值+/-1的二进信号波形，其自乘结果恒等于1；它经带通滤波器的滤波作用以后，便得到一个纯净的第二载波；但是，该重建载波的频率，是原信号频率的二倍（2fL2）；即，该重建载波的波长，仅为原信号波长的二分之一，而被称之为半波载波相位测量法。

3.3 L1-P/L2-P互相关测量法

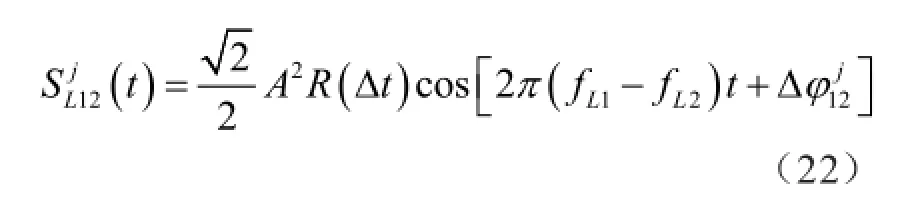
式（22）中的R(Δt)是L1-P码和L2-P码的互相关系数，当R(Δt)等于最大值1时，则可获得一个纯净的第一、二载波的差频信号。由此测得的载波滞后相位，是第一、二载波信号之差，其波长为

图6 P-L1/P-L2互相关测量法示意图

考虑到fL1=1575.42MHz和fL2=1227.60MHz，则知，λd=86.2cm；这意味着将第一载波的波长放大了4.5倍，而很有利于GPS动态载波相位测量的波数解算，且将λd叫做宽巷载波相位测量波长，后续章节还将进一步论述之。

3.4 互相关/平方律混合法

在2000年5月1日以前，GPS卫星发送的导航定位信号，均施加了人为降低测量精度的SA/AS技术，如果考虑到AS技术对第j颗GPS卫星导航定位信号的影响，则有该输入信号与接收机用C/A码辅助生成的P码[Pj(t)LO]进行互相关运算，并考虑到Pj(t-td) ×Pj(t)LO=1，则知互相关器的输出信号经过500kHz带通滤波器的带外噪声抑制后，而分成二路进入混频器（如图7所示），用其非线性特性的和频项，即，信号Sj

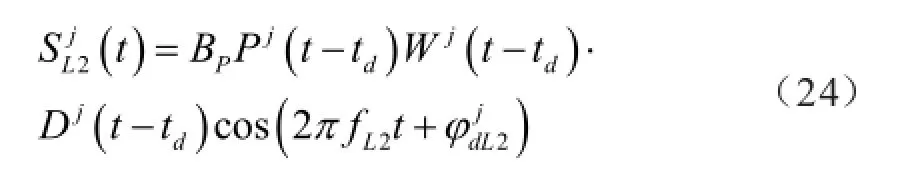
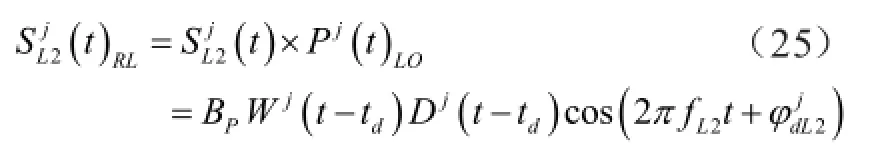
L2(t)RL在混频器中自乘而得

图7 互相关/平方律混合测量法

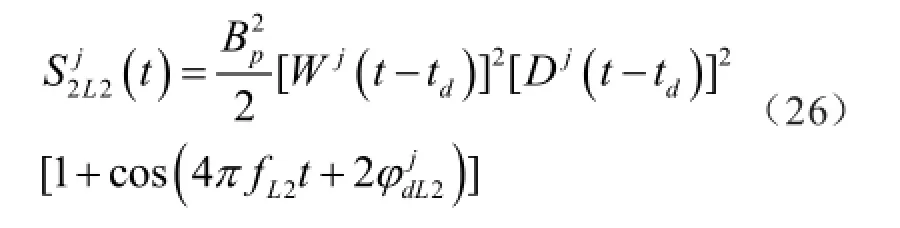
因Wj和Dj均为取值+/-1的二进信号波形，其自乘结果恒等于1，它经带通滤波器的滤波作用以后，便得到一个纯净的第二载波由Sj

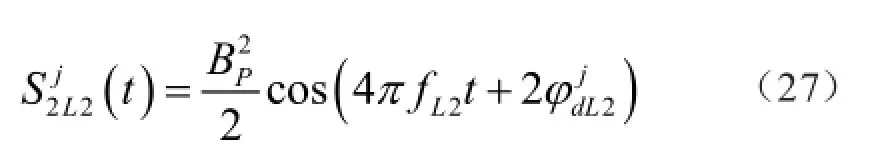
2L2(t)测得的载波滞后相位，是以半波长计量的。

3.5 Z-跟踪测量法

Z-跟踪测量法是美国Ashtech公司所开发的在AS技术影响下获取双频载波相位测量的专科技术。从图8可见，第j颗GPS卫星的第一导航定位信号的L1-Yj(t)码和接收机所产生的L1-P(t)LO码，经过CR-1互相关器处理后，送至WIF-1积分器/500kHz带通滤波器，后者从L1-Yj(t)码中提取出W码的估值信号，记作L1-Wˆ；与此同时，第j颗GPS卫星的第二导航定位信号的L2-Yj(t)码和接收机所产生的L2-P(t)LO码，经过CR-2互相关器处理后，送至另一个WIF-2积分器/500kHz带通滤波器，后者从L2-Yj(t)码中也提取出W码的估值信号，记作ˆ 。现将估值信号送到WIF-1积分器/500kHz带通滤波器，而将L1-Wˆ估值信号送到WIF-2积分器/500kHz带通滤波器。进而对L1-Wˆ 和L2、L2-Wˆ和L1分别进行积分运算，又通过500kHz带通滤波器的滤波作用，便可获得纯净的全波长的第一载波和第二载波，进而分别测得它们的滞后相位。

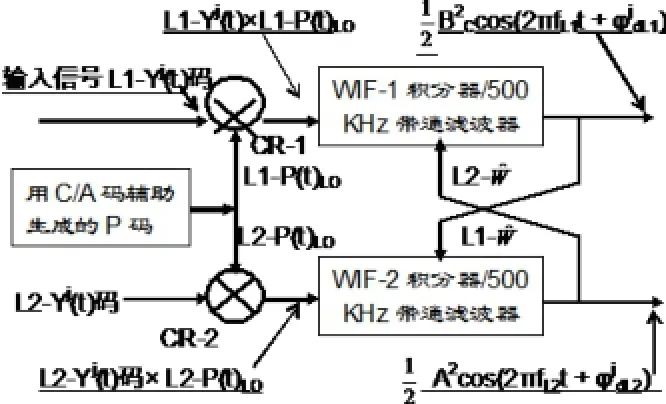
图8 Z-跟踪测量法

从上述可知，载波相位测量的全波长观测值、半波长观测值和组合波长观测值，均可用一定的电子硬件予以实施；即使用W码将P码变成了Y码（详见《GPS卫星导航定位原理与方法》一书的§3.5）以后，也能够用上述的一种电路，捕获和跟踪到第二载波，而实现双频载波相位测量。

4 结束语

综上所述，我们简要地论述了涉及GNSS载波相位测量的多普勒频移、波数和整周跳变等问题，并以GPS信号为例，简要地论述了用于载波相位测量的载波锁相测量法、平方律测量法、L1-P/L2-P互相关测量法、互相关/平方律混合法和Z-跟踪测量法；这对于我们研发高精度的GNSS信号接收机也许有一定的借鉴作用。■

[1] 刘基余．GPS卫星导航定位原理与方法（第二版）．北京：北京科学出版社，2008.6

[2] Lachapelle,G., GPS Theory and Applications, University of Calgary, Fall 2000, PP.310

GNSS Carrier Phase Measurements --Method of GNSS Navigation/Positioning (6)

Liu Jiyu
(School of Geodesy and Geomatics, Wuhan University, Wuhan, 430079)

GNSS carrier phase measurements, not only can be used for the static positioning of millimeter level accuracy, but also can be used for the kinematical positioning of centimeter level accuracy. Taking GPS signal as an example, this paper discusses several practical methods for measuring carrier phase.

GNSS signal; Carrier phase; GPS signal receiver

10.3969/J.ISSN.1672-7274.2017.02.001

TN96

A

1672-7274（2017）02-0001-06

刘基余，现任武汉大学测绘学院教授/博士生导师，兼任美国纽约科学院（New York Academy of Sciences）外籍院士、中国电子学会会士。主要研究方向是GNSS卫星导航定位/卫星激光测距技术，在国内外30余种中英文学术期刊上发表了280余篇相关研究论文，独著了（北京）科学出版社于2013年1月出版发行的《GPS卫星导航定位原理与方法》一书。他的主要业绩已分别载于美国于2001年出版发行的《世界名人录》（Who's Who in the World）、美国于2005年出版发行的《科技名人录》（Who's Who in Science and Engineering）和中国科学技术协会于2007年出版发行的《中国科学技术专家传略》工程技术编《电子信息科学技术卷2》等50多种国内外辞书上。