阻燃粘胶/腈氯纶混纺织物的热分解动力学研究

任元林，王秀丽，曾 倩，谷叶童，张 悦，秦一文，霍同国

(天津工业大学纺织学院，天津 300387)

阻燃粘胶/腈氯纶混纺织物的热分解动力学研究

任元林，王秀丽，曾 倩，谷叶童，张 悦，秦一文，霍同国

(天津工业大学纺织学院，天津 300387)

以阻燃粘胶纤维和腈氯纶为原料，通过控制以上两者不同混纺比制备了阻燃织物。根据热重分析(TG)探讨出阻燃粘胶与腈氯纶最佳混纺比为40/60，通过运用热分解动力学计算出阻燃粘胶/腈氯纶混纺比为40/60时混纺织物的热分解动力学方程为G(α)=[-ln(1-α)]n，并表明其非等温热分解机理属于随机成核和随后生长。

阻燃粘胶 腈氯纶 混纺织物 热分解动力学

0 前言

硅系阻燃粘胶纤维具有吸湿、透气、易染色等优良的特性，又因其制成的织物不仅手感好而且穿着具有舒适性，因而被广泛应用于各种纺织品领域，又因纤维属于不燃性纤维，LOI(极限氧指数)不低于28，且其废弃物具有自然降解的属性，因此硅系阻燃粘胶纤维是绿色环保型纤维[1-2]。腈氯纶是通过湿法或干法纺丝工艺将丙烯腈单体与偏二氯乙烯或氯乙烯化共聚物纺制而成；腈氯纶具有高阻燃性，LOI值达到26～34，且拥有与腈纶纤维很多相似的优点如类似羊毛的手感、色牢度好和强度高等，因而其常被用于多种阻燃织物中[3-4]。目前，国内对于阻燃粘胶纤维与腈氯纶混纺织物的热力学鲜有研究。

将硅系阻燃粘胶纤维与腈氯纶按照不同的混纺比纺制织物。并对织物进行热力学分析，探讨最佳混纺比，计算材料的活化能以及分析热分解机理。

1 实验

1.1 材料

腈氯纶：2.12dtex×39mm(抚顺阻燃聚丙烯腈纤维厂)；阻燃粘胶：2.30dtex×50mm(山东海龙公司)。阻燃粘胶纤维/腈氯纶分别按照以下混纺比进行探究：0/100、20/80、40/60、60/40、80/20、100/0。纺制纱线规格：线密度为40 tex、捻度为325 捻回数/m、捻向为Z捻。织造平纹梭织物，经纱和纬纱密度分别为：180根/10cm，155根/10cm。六种织物编号分别为：A1、A2、A3、A4、A5、A6。

1.2 测试方法与仪器

测试材料热稳定性主要采用热重分析法，热重分析法简称TG(Thermogravimetric Analysis)，是借助仪器控制温度，使用热天平测量物质的质量与温度之间关系的技术。热分析方法主要包括热重分析(TG)、差热分析(DTA)和差示扫描量热分析(DSC)等。从TG曲线中可以得到材料的失重温度范围、失重速率和残渣量等信息。

实验仪器：STA409PC热重差热分析仪，温度范围为室温至800 ℃，升温速率10 ℃/min，氮气保护。

2 结果与分析

2.1 热重分析

下页图1是混纺织物的TG曲线，下页图2是混纺织物的DTG曲线。

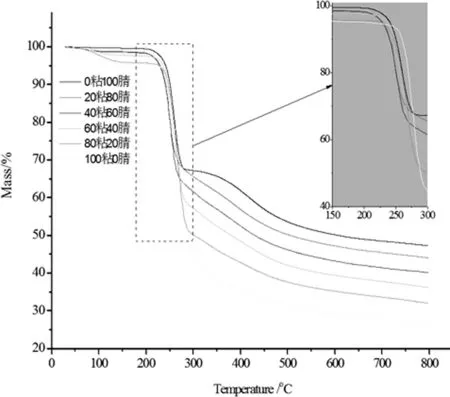
图1 混纺织物的TG曲线

图2 混纺织物的DTG曲线

从图1和图2可明显发现，材料的热分解过程可以大致分为三个主要阶段：(1)小于200 ℃的初始分解阶段；(2)200℃～300℃的快速分解阶段；(3)大于300 ℃的后期分解阶段。总体来看，混纺织物在初期的热失重、快速分解阶段的热失重速率和最终的残炭量方面差异显著。

在热分解初期阶段，A1和A5质量损失最为明显，这是由于阻燃粘胶的回潮率较高(回潮率为12%)，纤维中含有较多自由水分子或与氢键结合的水分子，在热解的初期就会蒸发散失而表现出显著的质量损失。而A6在初期阶段质量损失最小，几乎没有出现热分解速率峰，这主要是因为它的回潮率较低，仅为3.8%。同时不难发现，随着阻燃粘胶在混纺织物中比例的下降，织物的初期质量损失呈现出减小的趋势，再次证实了初期的质量损失主要是由于纱线中水分重量流失所引起，因而，阻燃粘胶在混纺织物中所占比例的高低是影响热分解初期特征的主要因素。

在快速分解阶段，混纺织物在分解温度先后和最大分解速率峰值等方面存在诸多不同。在分解的温度先后方面，A2和A3最先开始快速分解，之后依次为A5、A4、A6和A1，分解温度的先后与混纺比无直接关系，这很可能是由于阻燃粘胶纤维中阻燃剂与腈氯纶的相互作用引起的。同时，在DTG曲线上，可以发现A2和A3具有最低的热分解速率峰，表现出更加优良的热稳定性，对纱线的阻燃性能有重要影响(测得两种混纺比的纱线LOI分别为29.5和27.3)。

在热分解后期，混纺织物的分解趋势基本相同，但是残炭量随着粘胶纤维添加量的增加而呈下降趋势。这说明最终残炭量的高低主要由材料的混合比例所决定的。实验结果中，纯腈纶纱线的最终残炭量为47.27%，纯粘胶纤维纱线的最终残炭量为26.32%也很好的印证了这一点。

综上所述，在热分解过程中，A3即混纺比为40/60的织物在快速分解阶段可以实现提前分解，并且显著降低最高热解速率峰，整体表现出优异的热稳定性。因此， 以混纺比为40/60的织物进行热分解动力学分析。

2.2 热分解动力学

实验采用40%粘胶纤维与60%腈氯纶混纺的织物进行热分解动力学分析，采用NETZSCH STA 409 PG/PC为测试仪器，实验条件为氮气保护，升温速率分别设定为(10，20，30，40)℃·min-1,气体流速为20 mL·min-1，加热温度范围：室温至900℃，试样质量为9mg～10mg。图3为阻燃粘胶纤维/腈氯纶比例为40/60时，四种升温速率的TG分析图。

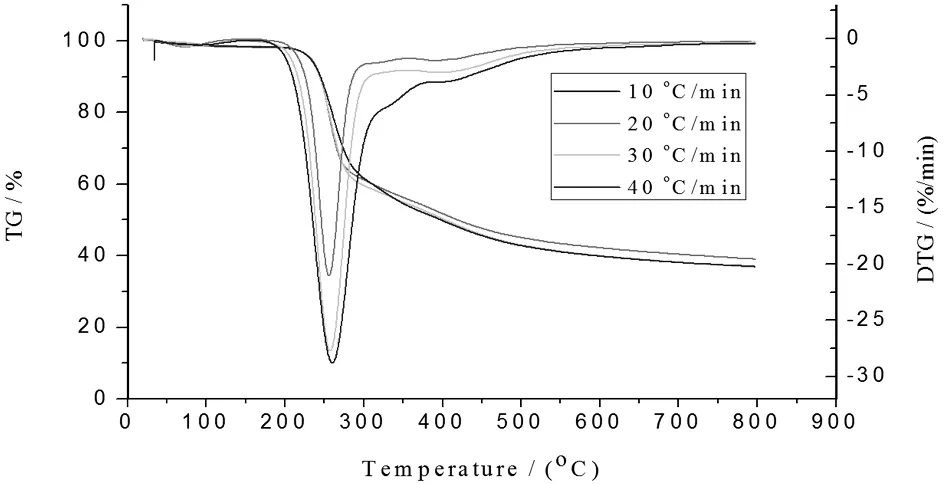
图3 阻燃粘胶纤维/腈氯纶比例为40/60时，四种升温速率的TG分析图

2.2.1 几种热分解动力学方法

对于热分解反应而言，其反应速率通常用下列式子(1)来表示：

dα/dt = Ae-E/RTf(α)

(1)

其式中，α：转化率(%)；A：表观指前因子(s-1)；E：反应活化能(kJ·mol-1)；R:普适气体常数(J·mol-1·K-1)，动力学常数；f(α):微分动力学模型，取决于反应机理。在程序升温速率条件下，升温速率β=dT/dt, 则上式(1)可转化为以下方程式(2)：

dα/dT = (A/β)e-E/RTf(α)

(2)

研究物质热降解的方法有很多，本研究采用的三种方法分别为Kissinger法[5]、Flynn-Wall-Ozawa法[6-7]和Satava-Sestak法[8]。

将方程(2)依次经过微分、积分整理后得Kissinger方程(3)：

(3)

则Flynn-Wall-Ozawa方程式(4)为

(4)

将(4)式改写后得Satava-Sestak方程式(5)如下：

(5)

其式中G(α)取30种积分机理函数形式。以上方程(5)被称为Satava-Sestak方程，对于固定的βi，将其对应的Tij和αij的数值代入方程(5)即得到包含ki个方程的一个方程组如下式(6)：

(i固定,j = 1,2, …ki)

(6)

2.2.2 活化能的计算

通过运用Kissinger法可计算出热分解过程中降解速率最大处时的动力学参数值，而利用Flynn-Wall-Ozawa法和Satava-Sestak法可算出热分解过程中任意点处的动力学参数值，表1为TG曲线图上所得到的参数和数据处理结果。

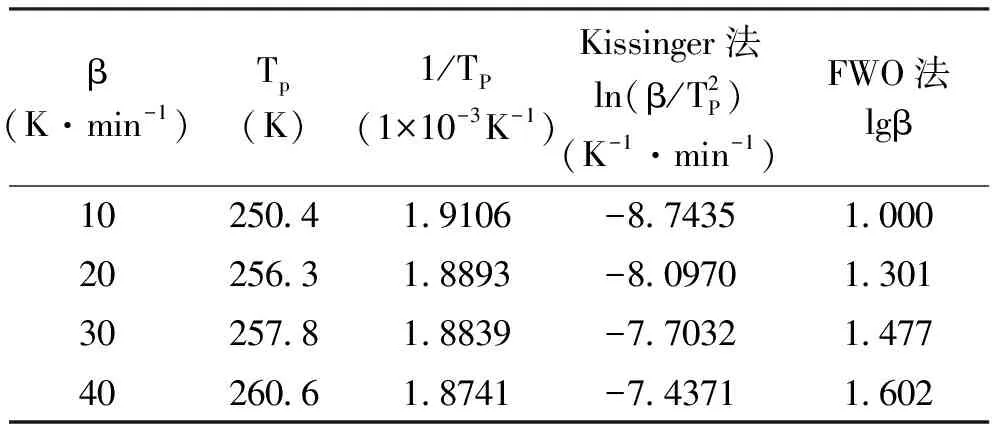
表1 TG测定的动力学基础数据

根据FWO法，以 lgβ对1/TP作图，利用最小二乘法对基本数据进行线性拟合，得到曲线如图4(b)所示，数据结果所示，直线斜率为-16766.25，截距为33.02，R(相关系数) = -0.9905，SD (标准偏差) = 0.0439，因此可求得Ea(活化能)= 305.22 kJ/mol，此法与Kissinger法所求得的EK一致。以上论证了所选热分解动力学方法的合理性。

此阻燃织物的热分解活化能较高，说明该阻燃织物的受热分解需要更高的能量，即说明该阻燃织物的热稳定性较好，这与热重曲线相一致。

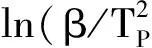
2.2.3 热分解机理推测

表2 30个常用函数

4种不同的升温速率下所得到的动力学方程及处理结果分别如表3所示。

表3 β= 10、20、30、40时，由Satava法所得到的2种机理函数方程及计算结果

3 结论

(1) 阻燃粘胶与腈氯纶混纺比为40/60时，织物的热稳定性更好，它在快速分解阶段可以实现提前分解，并且显著降低最高热解速率峰，整体表现出优异的热稳定性。

(2)由40%粘胶纤维与60%腈氯纶纤维混纺得到的阻燃织物的热分解动力学方程为G(α)=[-ln(1-α)]n，表明其非等温热分解机理属于随机成核和随后生长。由Kissinger法和FWO法求得的阻燃织物的热分解活化能分别为302.79 kJ/mol和305.22 kJ/mol。

[1] 孔庆岭,纪全.阻燃粘胶/Basofil混纺消防防护织物的研究[J].科技信息,2007(19):27,45.

[2] 朱张林.阻燃粘胶/阻燃腈纶纺织产品的开发[J].上海纺织科技，2009,2(37):30-31,45.

[3] 张建春,钟铮.腈氯纶阻燃纤维生产技术及应用[J].纺织导报，2000(2):15-17.

[4] 王晓明.阻燃腈氯纶纤维浅论[J].纤维生产，1998(4):14-16.

[5] Kissinger H E. Reaction kinetic in differential thermal analysis[J]. Anal Chem,1957,29(11):1702-1706.

[6] Flynn J H, Wall L A. A quick, direct method for the determination of activation energy from thermogravimetric data[J]. J Polym Sci, Part B: Polym Lett, 1966,4(5):323-328.

[7] Ozawa T. A new method of analyzing thermogravimetric data[J]. Bull Chem Soc Jpn, 1965,38(11):1881-1886.

[8] Satava V, Sestak J. Computer calculation of the mechanism and associated kinetic data using a nonisothermal integral method[J]. J Therm Anal, 1975,8(3):477-489.

2016-10-28

国家自然科学基金项目(51573134)

任元林(1971-)，男，博士，副教授，硕士生导师，研究方向：功能高分子材料。

TS101.92+3

A

1008-5580(2017)01-0079-04