基于改进六位置法的一种MEMS加速度计标定补偿方案

2017-02-24向高林路永乐龚大伟吴林志

重庆邮电大学学报(自然科学版) 2017年1期

关键词：加速度计刻度标定

向高林，路永乐，刘宇，龚大伟，吕玲，吴林志

(重庆邮电大学光电信息感测与传输技术重庆市重点实验室，重庆 400065)

基于改进六位置法的一种MEMS加速度计标定补偿方案

向高林，路永乐，刘宇，龚大伟，吕玲，吴林志

(重庆邮电大学光电信息感测与传输技术重庆市重点实验室，重庆 400065)

微机电系统(micro electronic mechanical system, MEMS)加速度计在测量过程中受安装误差、刻度因子及零偏影响，为提高MEMS加速度计的测量精度，在六位置法标定的基础上，提出一种改进的MEMS加速度计标定补偿方案。利用小波滤波对MEMS加速度计的原始测量值进行滤波，运用六位置法对6个位置的原始数据进行标定得到补偿模型。通过实验验证，MEMS加速度计测量精度由标定前的1.2 m/s2提高到0.01 m/s2，由MEMS加速度计解算的横滚角和俯仰角精度由标定前的1°提高到0.166 4°。

MEMS加速度计；小波变换；六位置法；标定

0 引言

相比传统惯性器件，微机电系统(micro electronic mechanical system, MEMS)传感器具有体积小、抗冲击振动强、低功耗、成本低以及可靠性高等优点[1-3]，因此，在石油钻井、航空、航海、汽车、工业控制以及消费电子产品等领域有着广泛应用[4]。MEMS加速度计的测量精度受安装误差、零偏和刻度因子的影响，从而使得它的应用范围受到限制[5]。MEMS加速度计作为惯性测量单元的核心器件之一[6-7]，通过建立误差模型对MEMS加速度计进行标定是很有必要的。

2009年，秦永元等人对于MEMS加速度计安装误差的校准是通过采用传统六位置法，即使用除以刻度因子后的实际MEMS加速度计值作为研究对象[8]。2012年，王小春等人在全温范围内对MEMS加速度计进行标定，同样是以MEMS加速度计实际输出值为研究对象[9]。然而，MEMS加速度计应用于实际工程中，它的刻度因子会随着外界因素的变化而发生改变，而并非一个常值，因此，在工程实践中，若将刻度因子当作定值必然会导致MEMS加速度计实际输出值产生误差，使得MEMS加速度计标定模型不准确，若单独对刻度因子进行补偿，目前还没有较为完善的刻度因子补偿方法，效果不是很理想。基于此，论文以实验室自主研制的基于MEMS惯性传感器的姿态仪为研究对象，提出了一种改进的六位置法对MEMS加速度计进行标定。该标定方案是以MEMS加速度计的原始数据为处理对象，避免了由于刻度因子不固定引起标定模型不准确的缺点。通常，有2种标定方法：一种是在各温度区间通过使用六位置法建立不同的误差标定模型；另一种是在全温范围内，利用六位置法建立一个统一的误差标定模型。考虑到工程应用条件的限制，论文采用了第2种标定方法，首先利用小波滤波对MEMS加速度计的原始数据进行滤波，目的在于减少噪声对MEMS加速度计原始数据的影响，再结合改进六位置法对MEMS加速度计的安装误差进行标定。经实验验证，MEMS加速度计经过标定模型标定后达到了较好的补偿效果，能够满足MEMS加速度计应用在工程领域的精度需求。改进六位置法标定模型计算量小，精度高，且易于实现。

1 MEMS加速度计输出模型

MEMS加速度计静止状态的输出值模型为

A=a0+K1×a1+K2×a1+K3×a1×a2

(1)

(1)式中：A表示它的原始输出值，单位为mV；a0表示它的原始零偏数据，单位为mV；K1为刻度因子，单位为mV/(m/s2)；K2代表MEMS加速度计的二阶非线性系数，单位为mV/(m/s2)2；K3为交叉耦合系数，单位为mV/(m/s2)2；a1表示敏感轴方向的MEMS加速度计值，单位为m/s2；a2表示与敏感轴方向垂直的MEMS加速度计值，单位为m/s2。对于MEMS加速度计而言，(1)式中交叉干扰项和非线性项造成的非线性误差低于5‰，我们在进行处理时忽略了这两项的影响，因此，MEMS加速度计原始输出值模型可表示为

(2)

传统六位置法是以输出值a1为研究对象进行标定，如果MEMS加速度计的性能较好，且外界因素变化不大，K1为固定值，但在实际工程应用中，由于外界环境的变化，会引起K1不是一个定值，从而造成输出值a1不准确，因此，采用传统六位置法对MEMS加速度计值a1进行标定，必然会造成很大的误差。基于此，论文以MEMS加速度计原始输出值A为研究对象，提出了一种改进六位置法。

2 标定算法介绍

2.1 小波变换的原理

设f(t)∈L2(R)，则连续函数的小波变换可表示为[10]

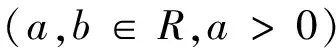
(3)

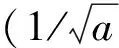
s(k)=A(k)+δW(k),(k=0,1,…,n-1)

(4)

(4)式中：s(k)表示加速度计的实际测量值；A(k)表示它的实际输出值；W(k)则表示MEMS加速度计在测量过程中受到的噪声。W(k)通常为高频噪声信号，A(k)是低频有用信号。在对MEMS加速度计测量值进行滤波时，通常将噪声考虑成高斯白噪声，小波系数的平均功率和尺度是成反比关系的。通过对MEMS加速度计原始测量值进行小波滤波，可以对噪声进行抑制，进而得到接近于实际的输出值A(k)。

2.2 改进六位置法的原理

在实际测量过程中，在对MEMS加速度计的输出模型进行分析后，可得到实验室自主研发的基于MEMS加速度计的惯性测量单元的安装误差模型为

(5)

(5)式中：Ax，Ay，Az分别表示加速度计X，Y，Z 3个轴的原始测量值，单位为mV；ax0，ay0，az0则分别表示各个轴的原始零偏值，单位为mV；Saxi，Sayi，Sazi(i=1,2)代表加速度计的安装误差系数；Kax，Kay，Kaz为MEMS加速度计的刻度因子。因此，该加速度计实际输出值的误差模型可表示成

(6)

本文采用的改进六位置法与传统六位置法的不同之处在于：传统六位置法是以MEMS加速度计原始测量值除以刻度因子之后的实际输出值作为研究对象，而改进六位置法则是以它的原始测量值为研究对象。

3 改进六位置法的标定

3.1 实验仪器

1)姿态仪。

本文以实验室自主研制的姿态仪为标定对象，它包括三轴MEMS加速度计、三轴MEMS陀螺仪、三轴磁力计以及一个气压计，如图1所示。

图1 基于MEMS传感器的姿态仪Fig.1 Attitude indicator based on the MEMS sensors

2)双轴电动转台。

902E-1双轴电动转台由北京航空精密机械研究所生产，如图2所示。转台速率精度为1×10-3(±0.01°/s～±100°/s)，角位置定位精度为5″。它在标定过程中的作用主要有两方面：一方面能够为MEMS加速度计的六位置标定提供参考位置；另一方面能够为改进六位置法标定效果的检验提供验证平台。

3.2 改进六位置法的标定方案

分别以地东南、天西南、西地南、东天南、南西地、东北天6个位置作为实验方位，通过改进六位置法对加速度计的误差系数进行确定。在对MEMS加速度计进行标定时选取的6个位置以及对应的重力加速度如表1所示。

图2 902E-1型双轴电动转台Fig.2 902E-1 biaxial electric turntable

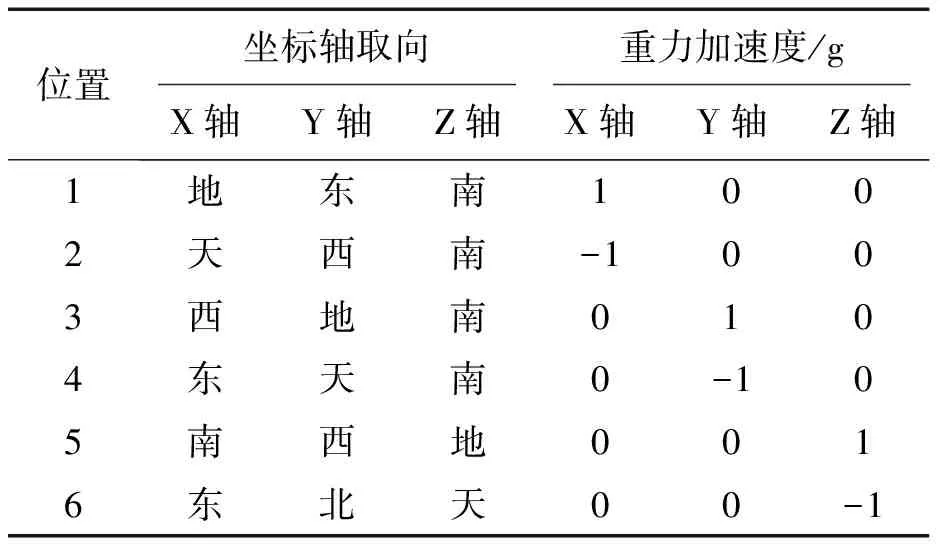
表1 六位置取向及对应的重力加速度

MEMS加速度计标定过程如下

1)先将姿态仪紧固在双轴电动转台上，并保证其敏感轴与转台的中心轴线平行；

2)接通姿态仪的电源，预热的时间约为30 min；

3)通过调整转台，保证MEMS加速度计分别为如表1中的第1，2，…，6个位置，每个位置采集X,Y,Z轴数据1 500组；

4)分别对每个位置的加速度计各轴的原始测量数据作小波滤波处理，并对滤波后的原始测量值取平均值，得到该位置下加速度计的原始测量值。

结合(5)式及表1，可得到1，2，…，6位置加速度计X轴的原值测量值依次为

(7)

1，2，…，6位置加速度计Y轴的原值测量值依次为

(8)

1，2，…，6位置加速度计Z轴的原值测量值依次为

(9)

由(7)式可得，标定模型中与X轴相关的系数分别为

(10)

由(8)式可得，标定模型中与Y轴相关的系数分别为

(11)

由(9)式可得，标定模型中与Z轴相关的系数分别为

(12)

3.3 标定系数的计算

在计算标定系数之前，通过对MEMS加速度计的原始测量值进行小波滤波，目的在于降低随机噪声对MEMS加速度计原始测量值的影响。本文对6个位置的MEMS加速度计分别采集1 500组原始数据，并进行滤波，以X敏感轴向下对准转台为例，滤波前滤波后对比图如图3所示。

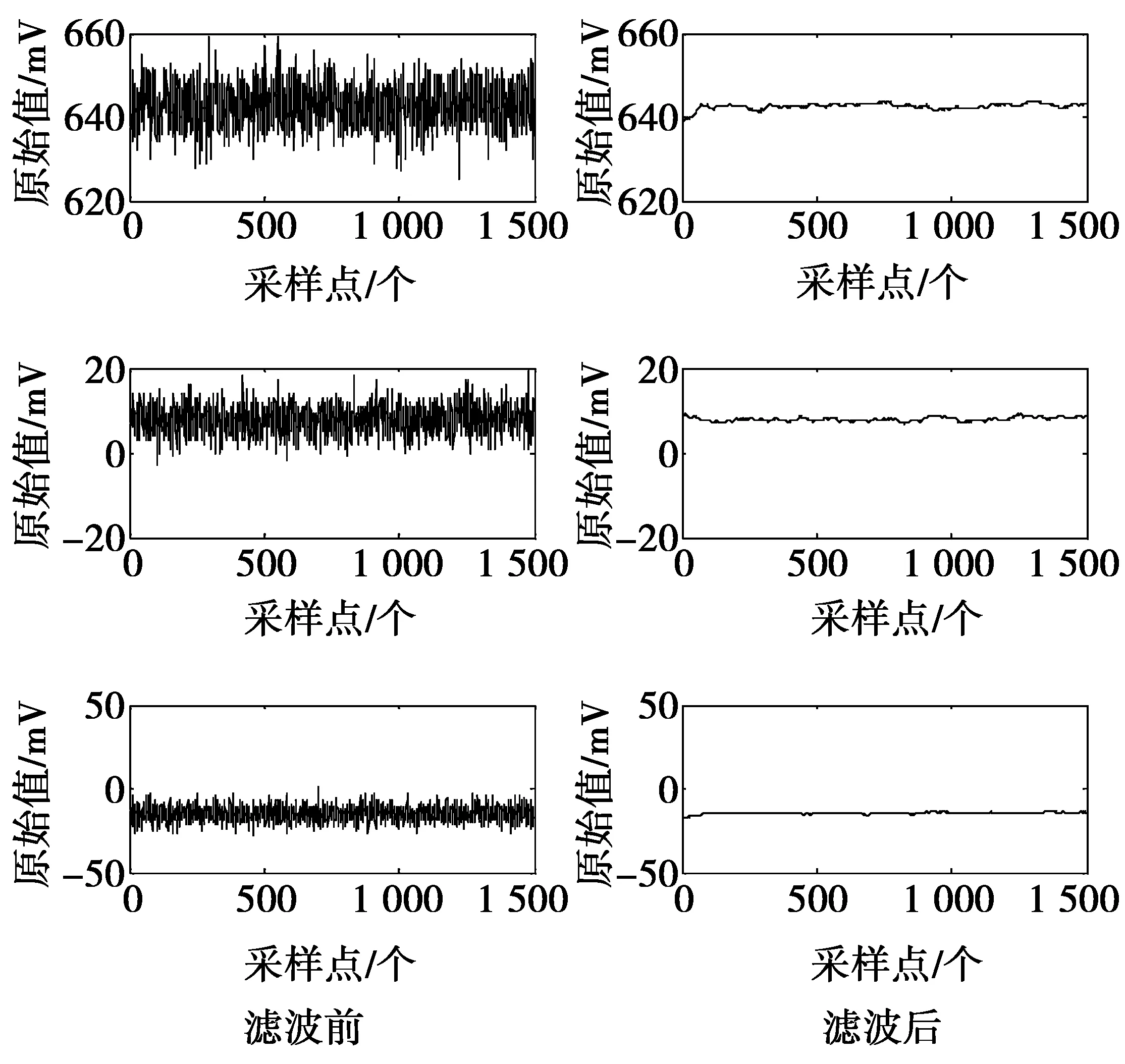
图3 各轴滤波前滤波后对比图Fig.3 Comparison diagram of before filtering and after filtering of the each axis

分别对滤波后MEMS加速度计X,Y,Z轴原始测量值取平均，得到1，2，…，6位置的加速度计各轴的原始输出值，如表2所示。

由(10)-(12)式可得到MEMS加速度计X轴、Y轴、Z轴的零偏和标定系数，如表3所示。

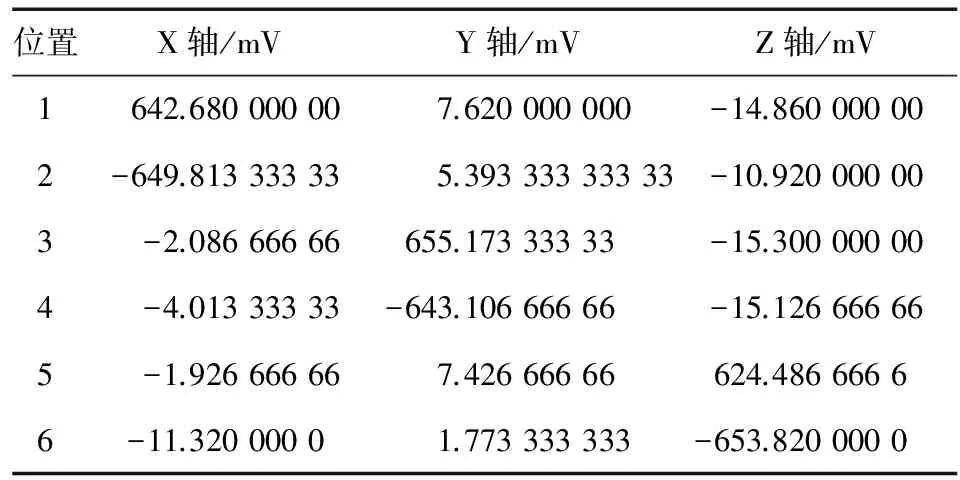
表2 MEMS加速度计6个位置各轴的原始输出值

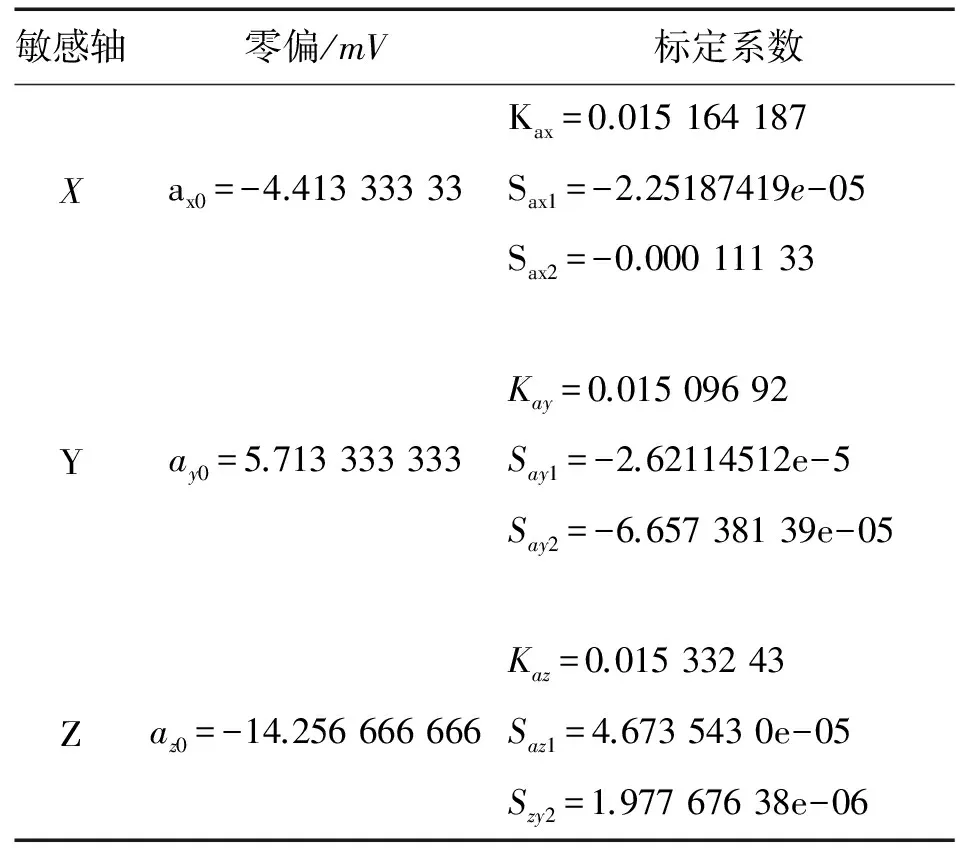
表3 MEMS加速度计各轴的零偏和标定系数

则姿态仪中MEMS加速度计的安装误差标定模型为

(13)

4 结果和讨论

4.1 标定验证流程

为了验证标定补偿模型的有效性和可行性，通过用(13)式对MEMS加速度计的原始测量值进行处理。流程图如图4。

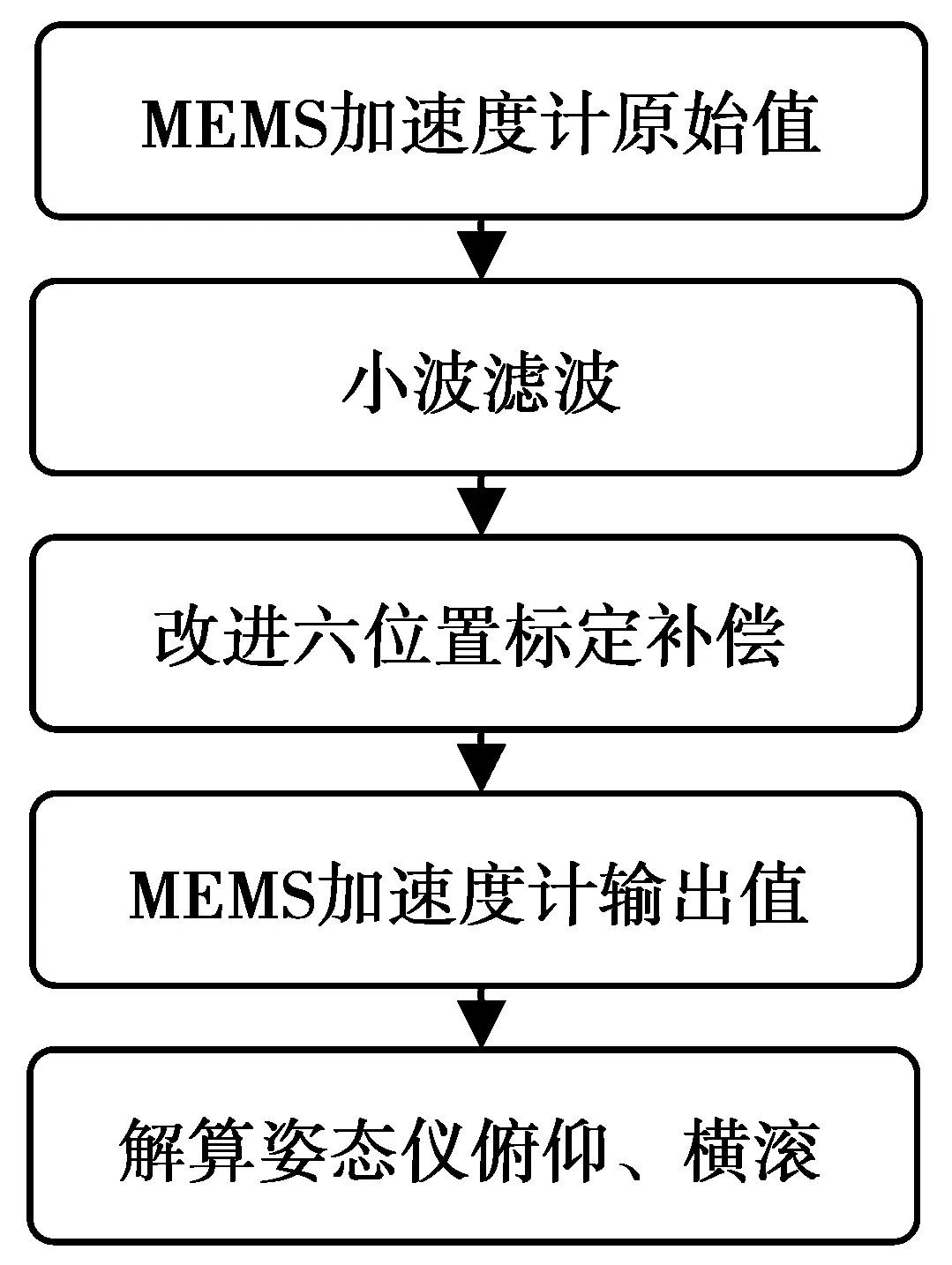
图4 流程图Fig.4 Flow diagram

4.2 实验结果分析

将MEMS加速度计的Y轴敏感轴向下垂直放在双轴电动转台上，通过采集若干原始数据，对原始测量数据进行小波滤波，将滤波后的原始测量数据代入(13)式得到标定后的加速度计值，与标定补偿前的数据进行比较，图5为滤波前与滤波后的MEMS加速度计原始值，MEMS加速度计值经过改进六位置法标定补偿后的数据如图6所示。

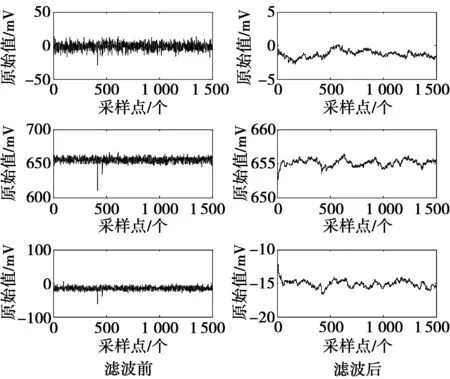
图5 滤波前与滤波后MEMS加速度计值Fig.5 Before filtering and after filtering of MEMS accelerometer value

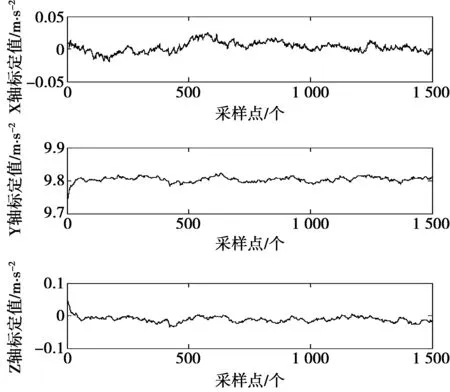
图6 标定后MEMS加速度计值Fig.6 Calibrated MEMS accelerometer value

将加速度计Y敏感轴向下垂直转台平面放置，经改进六位置法标定前后的输出值如表4所示。

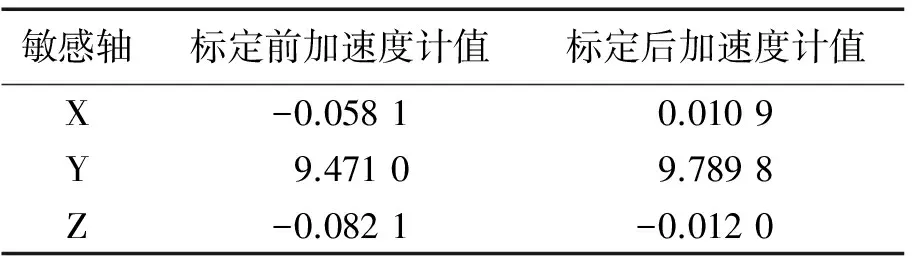
表4 MEMS加速度计标定前后输出值

由表4可知，补偿前X，Y，Z 3个轴的值分别为-0.058 1 m/s2，9.471 0 m/s2，-0.082 1 m/s2，补偿后分别为0.010 9 m/s2，9.789 8 m/s2，-0.012 0 m/s2，测量精度由标定前的1.2 m/s2提高到0.01 m/s2，效果较为明显。

加速度计输出值的一个用途是可以用来解算基于MEMS加速度计的姿态仪静止状态下的俯仰角和横滚角，因此，借此来验证MEMS加速度计安装误差的标定效果。论文通过俯仰角(-90°～90°)为例进行验证，利用转台控制姿态仪，保证其俯仰角依次为-80°，-60°，-40°，…，80°，用标定前和标定后的MEMS加速度计输出值分别计算姿态仪的俯仰角，得到结果如表5所示。

由表5可知，标定前，由加速度计解算俯仰角的平均绝对误差约为1°，而通过改进六位置法标定后，由MEMS加速度计解算的俯仰角更接近转台实际输入角度，平均绝对误差减小到0.164 4°，进而使得标定方案的可行性和准确性得到验证。

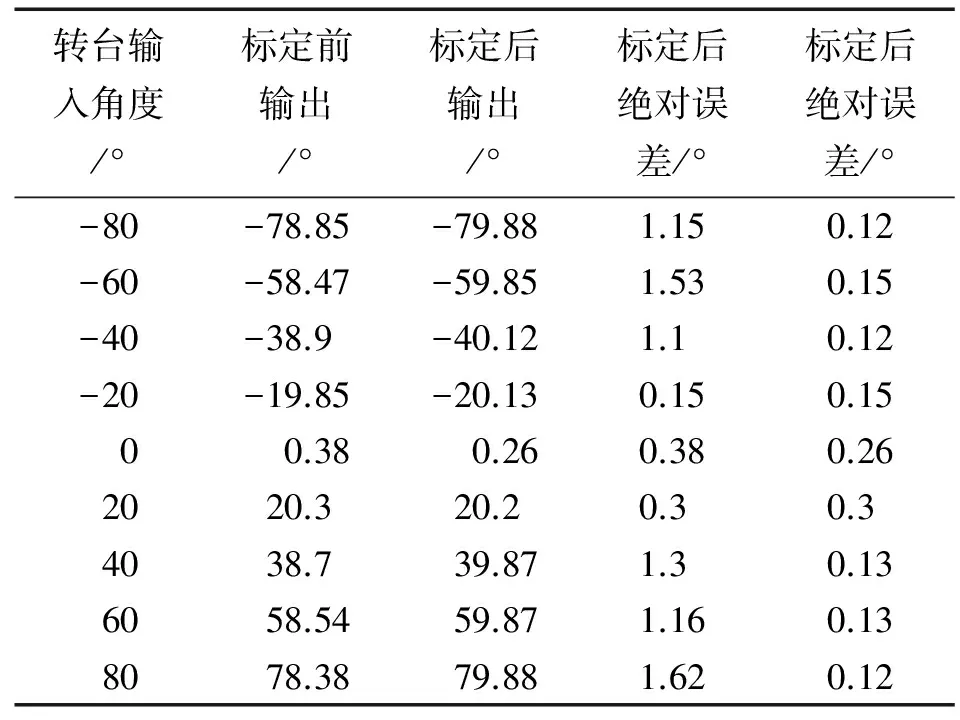
表5 标定前后加速度计解算俯仰角

5 结论

MEMS加速度计的测量精度主要受安装误差、零偏和刻度因子的影响。MEMS加速度计的误差标定模型是通过将小波滤波和改进六位置法相结合。分别对6个位置的加速度原始数据进行小波滤波后取平均值，减小高斯噪声对原始测量值的影响，再利用改进六位置法对MEMS加速度计进行标定。该标定模型能够克服传统六位置法由于刻度因子变化引起的误差。由实验验证，标定后MEMS加速度计的输出值更接近真实值，且加速度计解算的静态姿态角绝对误差由标定前的1°经过标定后减小为0.164 4°，使得该标定补偿方案的可行性和有效性得到验证。该标定模型具有计算量小，易于实现，精度较高等优点，对MEMS加速度计应用在工程领域有重要价值。

[1] YOO T S, LEE S C, HONG S K, et al. Smart Filter Design for the Localization of Robotic Fish Using MEMS Accelerometer[M]//Intelligent Autonomous Systems 12. Berlin Heidelberg: Springer. 2013: 509-518.

[2] LIU Y, XIANG G, CAO Y, et al. Research on the Temperature Compensation Algorithm of Zero Drift in MEMS Gyroscope Based on Wavelet Transform and Improved Grey Theory[J].Sensors & Transducers,2014,178(9).

[3] FROSIO I, PEDERSINI F, BORGHESE N A. Autocalibration of triaxial MEMS accelerometers with automatic sensor model selection[J]. Sensors Journal, IEEE, 2012, 12(6): 2100-2108.

[4] ROCHA L A, DIAS R A, CRETUE, et al. Auto-calibration of capacitive MEMS accelerometers based on pull-in voltage[J]. Microsystem technologies, 2011, 17(3): 429-436.[5] 尹杭, 张伟, 袁琳峰. 一种 MEMS 加速度计误差分析与校准方法[J].传感技术学报,2014,27(7):866-869. YIN Hang, ZHANG Wei, YUAN Linfen. An Error Analysis and Calibration M ethod of M EM S Accelerometer[J]. Chinese journal of sensors and actuators, 2014, 27(7): 866-869.

[6] 彭孝东,张铁民,李继宇,等.三轴数字MEMS加速度计现场标定方法[J].振动.测试与诊断, 2014, 34(3): 544-548. PENG Xiaodong, ZHANG Tiemin, LI Jiyu, et al. Field Calibration of Three-Axis MEMS Digital Acceleration[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(3): 544-548.

[7] FANG B, CHOU W, DING L. An optimal calibration method for a MEMS inertial measurement unit[J]. Int. J. Adv. Robot. Syst, 2014, 11(14): 57516.

[8] 宋丽君, 秦永元. MEMS 加速度计的六位置测试法[J]. 测控技术, 2009, 28(7): 11-13. SONG Lijun, QIN Yongyuan. Six-Position Testing of MEMS Accelerometer[J]. Measurement & Control Technology, 2009, 28(7): 11-13.

[9] 王小春,李荣冰,杭义军,等.MEMS加速度计误差的高精度标定方法[J].微纳电子技术,2012,11:743-748. WANG Xiaochun, LI Rongbing, HANG Yijun, et al. High-Precision Calibration Method for the Error of MEMS Accelerometers[J]. Micronanoelectronic Technology, 2012, 11: 743-748.

[10] 高成. MATLAB小波分析与应用[M]. 北京: 国防工业出版社, 2007. GAO Cheng. Analysis and application of MATLAB wavelet[M].Beijing:National Defense Industry Press,2007.

(编辑：张诚)

A calibration and compensation scheme of MEMS accelerometer based on the improved six position method

XIANG Gaolin, LU Yongle, LIU Yu, GONG Dawei, LV Ling, WU Linzhi

(Chongqing Municipal Level Key Laboratory of Photoelectronic Information Sensing and Transmitting Technology, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China)

MEMS accelerometer is influenced by installation error, scale factor and zero bias in the process of measuring. In order to improve the measurement accuracy of MEMS accelerometer, an improved calibration and compensation scheme of MEMS accelerometer based on six position method was proposed. Wavelet filtering was utilized to filter original measurements of MEMS accelerometer, and six position method was used to calibrate six position so as to get the compensated model. Verified by the experiments, the measurement accuracy of the MEMS accelerometer was raised to 0.01 m/s2from the 1.2m/s2, and the precision of roll angle and pitch angle calculated by MEMS accelerometer was raised to 0.166 4° from the 1° before calibration.

MEMS accelerometer; wavelet filtering; six position method; calibration

10.3979/j.issn.1673-825X.2017.01.010

2015-07-23

2016-04-10 通讯作者：路永乐 luyongle08@163.com

国家自然科学基金资助项目(51175535);国际联合研究中心科技平台与基地建设(cstc2014gjhz0038)；重庆市研究生科研创新项目(CYS15163)；重庆邮电大学博士启动基金(A2015-40);重庆邮电大学自然科学基金(A2015-49)

Foundation Items：The National Natural Science Foundation of China(51175535); The Science and Technology Platform and Base Construction of International Joint Research Center(cstc2014gjhz0038)；The Graduate Student Research Innovation Project of Chongqing(CYS15163); The Dr. Start-up Fund of Chongqing University of Posts and Telecommunications(A2015039); The National Natural Science Foundation of Chongqing University of Posts and Telecommunications

TN212

1673-825X(2017)01-0062-06