湍流效应对雨滴表面粒子捕集过程的影响

华凤皎,亢燕铭,钟 珂 (东华大学环境科学与工程学院,上海 201620)

湍流效应对雨滴表面粒子捕集过程的影响

华凤皎,亢燕铭*,钟 珂 (东华大学环境科学与工程学院,上海 201620)

为考察湍流运动对捕集效率的影响,本文在不同湍流强度下分别模拟了 4种直径雨滴对不同粒径粒子的捕集过程.根据湍流场中粒子捕集过程的特征,通过引入碰撞概率的概念,重新定义了适用于湍流状态下捕集效率的计算公式,并在此基础上分析研究了湍流捕集效应对捕集效率的影响.结果表明,所有粒径粒子的碰撞概率分布特征都会受到背景湍流强度的影响,尤其对 5µm及以下粒子影响明显.湍流捕集效应对捕集效率的影响与粒子密度和粒径直接相关,与雨滴尺寸无关.

气溶胶粒子；雨滴；湍流强度；捕集效率

近几年来,霾天气在我国多数大城市频繁出现,已成为热点环境问题.显然,大气的自然净化过程是霾的重要清除机制之一.在自然净化过程中,气溶胶粒子主要通过干沉积和湿清除从大气中被移除.尽管干沉积的贡献率更高、更有效,但湿清除在降雨过程中单位时间内的清除效率更高.在多雨地区,湿清除对大气环境的净化作用不可忽略.目前在全球和区域大气气溶胶输送模式及空气质量评估模式等的研究中[1-4],尤其关注气溶胶湿清除率,并认为其计算的准确性将影响到这些模式对气溶胶输送过程估计的精度.

Slinn公式是目前常用的雨滴对粒子捕集效率的半经验公式[5],但它是在以雨滴表面绕流为层流的基础上得到的,而大气运动具有明显的湍流特征,大气湍流强度甚至可能达到 50%[6,7].背景大气流场的湍动效应通过影响粒子轨迹来改变雨滴对粒子的捕集效果.尽管最近几年来,已有不少研究者指出[8-11]应该考虑这种湍流扰动对雨滴捕集气溶胶粒子的影响,但相应的研究结果目前还很少见到.通过分析背景湍流捕集效应对雨洗过程中粒子轨迹的干扰和畸变,得出惯性粒子在湍流状态下被雨滴捕获的效率将大于层流时的捕集效率,但没有对湍流效应产生的具体影响做进一步研究[12].

计算流体力学(CFD)方法是求解湍流运动的常用手段,通过耦合求解流动方程和粒子运动方程,可得到湍流状态下雨滴对粒子的捕集效率.与实测相比,CFD模拟可节省大量实验成本,并极大地缩短问题求解时间从而降低研究成本.因此,本文将采用经过实验数据验证后的CFD模型进行上述问题的求解.由于不同湍流强度下,气流速度的脉动幅度不同,进而导致粒子随湍流脉动随机游走的过程中运动轨迹差别较大,最终造成湍流对粒子捕集效率的作用受湍流特性和粒子特性的影响很大,故本文将针对不同尺寸的雨滴和粒子来分析湍流强度对捕集过程和捕集效率的具体影响,以便为修正清除效率估计式(即Slinn公式)提供必要的科学依据.

1 数值方法与验证

1.1 物理模型和计算工况

实际大气中雨滴以终端沉降速度u0下落,为了简化问题,将下落雨滴视为静止液体球,气流以恒定速度 u0流经雨滴.考虑雨滴球体的对称性,取雨滴的1/4进行建模,如图1所示.计算域入口边界与雨滴前向驻点间的距离取为雨滴直径的5倍,计算域出口与雨滴后向驻点的距离取为 8倍直径.为避免计算区域端部效应的影响,雨滴表面与计算域其余边界的距离均取5倍直径,将紧邻雨滴表面处的网格做加密处理,网格最小尺寸为1.0µm.计算区域与网格处理详见文献[12-13].

雨滴终端速度[1]u0(dw)如下:

式中:dw为雨滴直径,cm.针对本文研究的雨滴直径,表1给出了不同雨滴对应的终端速度.

湍流强度是衡量气流湍流脉动大小的参数,气溶胶粒子随气流运动过程中受到大气湍流脉动和气流速度的影响,从而增加粒子运动轨迹的随机脉动性.为研究湍流强度对雨滴-粒子碰撞概率和捕集效率的影响,模拟了 5种背景湍流强度I0情况下dw=800µm雨滴分别对5种粒径粒子(dp=2.5、3.5、5、7和10µm)进行捕集;在研究雨滴直径对湍流捕集效应的影响时,选取相同的湍流强度I0=15%,模拟4种雨滴直径(dw=100、200、 400和800µm)对5种粒径粒子(dp=2.5、3.5、5、7和 10µm)的捕集;讨论粒子密度对湍流捕集效应的影响时,模拟湍流强度为 I0=50%,雨滴直径dw=800μm 时,5种粒径粒子(dp=2.5、3.5、5、7和10µm)密度分别为ρp=1500和2800kg/m3时被雨滴捕集的效率.

图1 计算模型示意Fig.1 Schematic diagram of the computational model

表1 不同直径雨滴对应的终端沉降速度Table 1 Terminal velocities corresponding to different diameter raindrops

1.2 计算方法与边界条件

本文采用标准 k−ω模型[14-15]对雨滴附近湍流流场进行模拟,其中壁面湍流特征用标准壁面函数描述,采用有限容积法离散控制方程,对离散方程的差分采用二阶迎风格式.假定计算域入口流速均匀,入口边界设为 inlet,出口边界设为outflow,即该流出区域的质量流率和流入区域的质量流率相等.将雨滴视作硬球,即表面无滑移,计算域的壁面设为有滑移壁面.粒子视作实心球,并假设粒子间无凝并行为.为了与经典实验数据比较并验证数值模型以获得简明结果,在数值程序中,仅考虑重力、布朗力和Saffman升力.控制方程如下:

连续性方程

动量守恒方程

湍流动能k和扩散速率ω的输运方程

粒子运动的控制方程

式中:Fg是重力项;FB为布朗力;FL为Saffman升力,表达式如下:

式中:ζ是均值为0、方差为1的高斯随机函数;Δt是颗粒的时间步长;S0是光谱强度函数;K=2.594; dij为流体变形速率张量.

1.3 模型的合理性验证

已有不少研究者对于层流条件下球形捕集体上的粒子惯性捕集进行了实验研究[17-21].为验证本文采用程序的可靠性,以下以雨滴直径dw=800μm 为例,模拟了层流下惯性粒子在雨滴表面的捕集效率.图2给出了模拟计算结果与已有文献实测数据的比较(图中E为捕集体对粒子的捕集效率,St为粒子的Stokes数[22]).

图2 球形捕集体上粒子惯性捕集效率的比较Fig.2 Comparison of calculated efficiencies of aerosols on a sphere by impaction vs previous results

由图2可见,在只考虑惯性碰撞机制时,捕集效率的模拟结果与文献中给出的一系列实测值基本一致.数值结果还表明,与 Slinn公式[5]求得的惯性效率相比,本文计算曲线更接近实测结果,而Langmuir和Blodgett的结果与所有实验值都偏离较远.因此,本文采用的数值程序可以用于对粒子运动轨迹的计算和雨滴对粒子捕集效率的模拟和估计.

2 结果与讨论

2.1 背景湍流强度对雨滴附近湍流场的影响

图3给出了背景湍流强度分别为I0=25%和50%时,dw=800μm 雨滴附近流场的湍流强度及流线的分布特征.

从上图中容易看出,雨滴上半游的气流湍流强度自入口向远场扩散,当雨滴对气流运动产生阻碍作用时,气流扰动剧烈,湍流强度显著增强.此外,尽管湍流强度不同,但雨滴附近的湍流强度等值线轮廓和流线相似,表明平均流场特征不受背景湍流强度的影响.

图3 雨滴附近流场湍流强度及流线分布Fig.3 Distributions of the turbulent intensity and streamlines near a raindrop

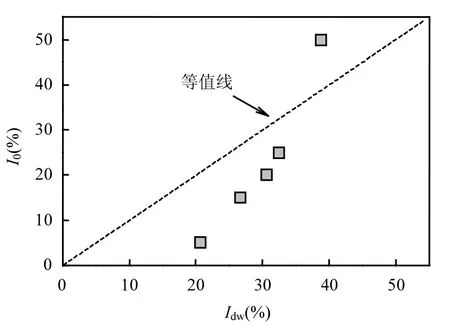
图4 雨滴迎风面附近湍流强度与背景流场湍流强度的相关性比较Fig.4 Comparison of correlations between turbulent intensity near windward side of a raindrop and background turbulent intensity

图4给出了雨滴迎风面附近(距离雨滴迎风面中心0.01dw处)投影面积上的平均湍流强度Idw与背景湍流强度I0的相关性,可以看到,雨滴附近的湍流强度随着背景湍流强度的增大而增加.当背景湍流强度较小时,雨滴附近湍流强度远大于背景湍流强度,且随着背景湍流强度的增大,二者逐渐接近,直至背景湍流强度大于雨滴附近湍流强度.不同的背景湍流强度将造成不同的局部气流扰动,从而直接导致雨滴对粒子的捕集效果发生变化.

2.2 雨滴捕集粒子的湍流捕集效应

层流状态下,粒子的运动轨迹与释放位置一一对应,因此存在如图1所示的临界位置y0,即粒径为dp的粒子极限轨迹对应的释放位置.所有在中心对称轴线的距离大于 y0的位置处的释放粒子,其运动轨迹将全部绕过雨滴逃逸,小于y0位置释放的粒子轨迹全部碰撞到雨滴表面被捕集.为此,层流状态时雨滴对粒子的捕集效率 EL(dw,dp)的定义为:

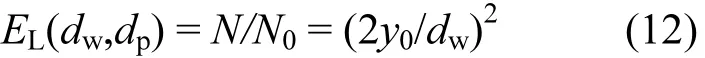
式中:dw为雨滴直径,μm;dp为粒子直径,μm;N为被捕集的粒子数,个;N和N0分别为被捕集的粒子数和投影面积上释放的总粒子数,个.

但是在湍流流场中由于受到气流脉动的影响,粒子轨迹将不具有层流状态时的唯一性,而具有一定的随机性,即在层流状态下无法被捕集的粒子,在湍流背景场中却可能被雨滴捕获,而在层流状态下一定会被捕集的粒子在湍流背景下也有可能不会被捕集.为此,本文引入碰撞概率ε(dw,dp,Y)来分析湍流下捕集效率的微观图像,其中无量纲释放距离 Y=y/y0.碰撞概率定义为从位置y处发出的粒径为dp的粒子与直径为dw雨滴发生碰撞而被捕集的可能性.

图5给出了不同背景湍流强度下dw=800μm的雨滴对不同粒径粒子的碰撞概率沿无量纲释放位置Y(Y=y/y0)的分布图.由图可以看到,碰撞概率随着粒子无量纲释放位置Y减小而增大.这是因为粒子运动轨迹首先受到惯性力控制,湍流在此基础上通过速度脉动影响粒子运动轨迹,故靠近雨滴中心对称轴线释放的粒子的碰撞概率较大.对于大粒子,碰撞概率都在Y小到一定值时增加到 100%,而对于小粒子,惯性力作用较弱,湍流干扰对粒子运动轨迹影响非常大,使得即使在Y=0处释放的粒子碰撞概率也无法达到100%.

由图5还可以看到,随着背景湍流强度的增大,湍流扰动作用相对于惯性力的作用增强,导致碰撞概率达到100%对应的临界位置Yc不断减小,使碰撞概率随粒子释放位置 Y的变化曲线更加偏离层流状态时的特征.

图5 湍流强度对雨滴-粒子碰撞概率的影响Fig.5 Influence of turbulent intensities on the collision probabilities between a raindrop and aerosols

上述模拟计算结果表明,在湍流脉动作用下,从雨滴上游任意位置y处发出的粒子,碰撞到雨滴表面的概率都介于 0～100%.这就意味着,考虑了湍流捕集效应后,层流下的捕集效率预测公式(12)不再适用.需要根据湍流状态下粒子与雨滴的碰撞概率特征重新定义适用于湍流场的捕集效率.

2.3 湍流脉动对捕集效率的影响

由于不同的释放位置 Y对应的碰撞概率以及对应的雨滴投影面积均不同,本文将雨滴的整个圆形投影区域分成若干个捕集微元环dS,如图6所示.

图6 湍流捕集效率计算示意Fig.6 Schematic diagram of calculating turbulent collection efficiency

释放位置 y+dy对应的投影圆环面积为2πydy,球形捕集体周围流场关于轴对称的特性使得Y值与碰撞概率ε(dw,dp,Y)为一一对应关系.根据对称性原理,每个捕集微元环对应的碰撞概率可以认为是一个定值.因此,湍流场中粒子的捕集效率可表示为:

通过数值模拟计算可以得到湍流场中在不同Y值释放的粒子与雨滴的碰撞概率,为便于利用数值结果计算雨滴对粒子的捕集效率,将上式改写为:式中:y1,y2,…… yn分别为第1,2,…n个捕集微元环外圆半径,μm;ε1,ε2,……εn分别为 y1,y2,……yn位置处对应的碰撞概率.

根据图 5的数值模拟结果和式(14),可以计算得到不同湍流强度时粒子的捕集效率.图7给出了5种湍流强度下dw=800μm雨滴对不同粒径粒子的捕集效率.

由图 7可知,较小粒子(dp=2.5～5μm)捕集效率随着湍流强度的增大而升高,并且粒径越小,湍流对捕集效率的增大作用越显著.而较大粒子尽管碰撞概率曲线(图5)受湍流的影响程度随湍强的增大而增大,但捕集效率却几乎不受湍流强度影响.相同的湍流强度下,捕集效率均随着粒径的增大而增加.

图7 不同湍流强度下粒子捕集效率的比较Fig.7 Comparison of collection efficiencies of aerosols with different turbulent intensities

2.4 雨滴尺寸对湍流捕集效应的影响

由于5μm以上大粒子的捕集效率受湍流影响不明显,因此,本文针对2.5和5μm粒子研究雨滴尺寸对上述湍流捕集效应的响应.图8分别给出了背景湍流强度I0=15%时,dp=2.5和5μm粒子与不同直径雨滴的碰撞概率曲线.

图8的结果表明,dp=2.5μm的粒子在大雨滴上的碰撞概率略高于在小雨滴上的碰撞概率,这是由于dp=2.5μm粒子在靠近雨滴中轴线释放时,受布朗扩散作用影响较大,所以,被不同直径雨滴捕集的概率随机性亦较大.但总体上看,雨滴尺寸对粒子的碰撞概率影响不大.原因是阻碍物周围流场特征主要受其形状影响,而本文研究的各种尺寸的雨滴均视为球形.因此,不同尺寸雨滴附近流场湍流特征也基本相同,故捕集效率对湍流效应的响应便近似相同.

图8 雨滴直径对湍流捕集效应的影响Fig.8 Influence of raindrop diameters on turbulent collection effect

2.5 粒子特性对湍流捕集效应的影响

由图5可以看出,在湍流流场中粒径dp越大,受到的惯性作用越显著,与雨滴发生碰撞的概率ε (dw,dp,Y)越接近层流下两点垂直式的碰撞概率分布,表明湍流捕集效应随着粒径增大而减小.

图9比较了ρp=1500和2800kg/m3粒子在背景湍流强度为I0=50%时与dw=800μm雨滴的碰撞概率.由图可知,粒子密度越小,湍流捕集效应越明显,但不同粒径粒子受密度的影响程度不同.图9(a)表明,当dp=2.5μm,ρp=1500kg/m3时,雨滴与粒子的碰撞概率很低,并且与释放位置Y相关性很小.而ρp=2800kg/m3时,碰撞概率明显增高,且与释放位置相关性很强.这是因为粒子受到的惯性力随密度增大而增大,密度较小的dp=2.5μm粒子运动轨迹几乎完全受控于湍流脉动,惯性力相对于湍流作用力较弱.由图9(b)可知,对于大粒子,虽然较小密度会导致惯性力减小、碰撞概率受到的湍流捕集效应增大,但由于粒径较大,保证了粒子受到的流场惯性力不会过小,因此,小密度和大密度粒子碰撞概率分布规律均与释放位置 Y密切相关.

图9 粒子密度对湍流捕集效应的影响Fig.9 Influence of particle densities on turbulent collection effect

图10 层流和湍流状态下捕集效率的比较Fig.10 Comparison of the collection efficiencies between laminar and turbulent flows

图10给出了I0=50%和层流下dw=800µm雨滴对不同密度粒子的捕集效率.可以看到在湍流作用下,大密度粒子和小密度粒子的捕集效率都有所提高.这是因为相对于层流,尽管湍流捕集效应降低了Y较小位置释放粒子的碰撞概率,但增大了Y较大位置释放粒子的碰撞概率,而后者对应的圆环面积[图 6(b)]大于前者,使得雨滴捕集体有效捕集面积增大,最终提高了粒子的捕集效率.

为了明确湍流对不同密度和不同粒径粒子捕集效率的影响,定义粒子捕集效率的湍流增加率λ为:

式中:EL,ET分别为该粒径粒子对应的层流和湍流捕集效率.

图11分别给出了dw=800µm的雨滴对不同密度粒子捕集效率的湍流增加率.由图11可以看到,粒子的密度和粒径dp越小,湍流脉动对捕集效率的增加率λ越大.湍流对dp=10µm的2种密度粒子捕集效率的提高幅度分别为 8.3%和 9.5%.但对于dp=2.5µm的2种密度粒子,提高幅度高达72%和120%.

图11 不同粒子密度下捕集效率的湍流增加率Fig.11 Turbulent increase percentages of collection efficiency with different particle densities

3 结论

3.1 由于湍流脉动对粒子运动轨迹的随机干扰,雨滴对不同位置释放的粒子的捕集效果与层流完全不同.为此,原有的层流状态下粒子捕集效率的计算公式不再适用于湍流场,本文通过定义碰撞概率的概念,重新定义了适用于湍流状态下的捕集效率计算公式.

3.2 所有粒径粒子的碰撞概率分布特征都会受到背景湍流强度的影响,但捕集效率受到湍流强度明显影响的粒径范围为dp≤5μm.

3.3 由于不同大小的球形阻碍物对周围流场的干扰作用相似,因此,雨滴尺寸对碰撞概率分布规律的影响可以忽略.

3.4 随着粒子密度和粒子直径的减小,粒子的碰撞概率分布将越分散,湍流脉动对捕集效率的增大作用越显著.

[1] Wang X, Zhang L, Morna M D. Uncertainty assessment of current size-resolved parameterizations for below - cloud particle scavenging by rain [J]. Atmospheric Chemistry & Physics, 2010, 10(12):5685-5705.

[2] Wang X, Zhang L, Morna M D. On the discrepancies between theoretical and measured below-cloud particle scavenging coefficients for rain – a numerical investigation using a detailed one-dimensional cloud microphysics model [J]. Atmospheric Chemistry & Physics, 2011,11(22):11859-11866.

[3] Henzing J S, Olivie D J L, van Velthoven P F J. A parameterization of size resolved below cloud scavenging of aerosols by rain [J]. Atmospheric Chemistry & Physics, 2006, 6(11):3363-3375.

[4] Sportisse B. A review of parameterizations for modeling dry deposition and scavenging of radionuclides [J]. Atmospheric Environment, 2007,41(13):2683-2698.

[5] Slinn W G N. Precipitation scavenging. In: Atmospheric Sciences and Power Production 1979. Washington, D.C.: Division of Biomedical Environmental Research, U.S. Department of Energy, 1983.

[6] 高会旺,顾 明,王仁磊,等.北黄海海域大气湍流强度特征及风速标准差相似性分析 [J]. 中国海洋大学学报, 2009,39(4):563-568.

[7] 徐玉貌,周朝辅,李振华,等.广州市近地层大气的湍流微结构和谱特征 [J]. 大气科学, 1993,17(3):338-348.

[8] Feng J. A 3-mode parameterization of below-cloud scavenging of aerosols for use in atmospheric dispersion models [J]. Atmospheric Environment, 2007,41(32):6808-6822.

[9] Pinsky M B, Khain A P. Turbulence effects on droplet growth and size distribution in clouds - A review [J]. Journal of Aerosol Science, 1997,28(7):1177-1214.

[10] Andronache C, Gronholm T, Laakso L, et al. Scavenging of ultrafine particles by rainfall at a boreal site: observations and model estimations [J]. Atmospheric Chemistry & Physics, 2006, 6(12):4739-4754.

[11] Khain A P, Pinsky M. B. Turbulence effects on the collision kernel, II: Increase of the swept volume of colliding drops [J]. Quarterly Journal of the Royal Meteorological Society, 1997, 123(542):1543-1560.

[12] 华凤皎,刘晓燕,亢燕铭. 雨滴表面惯性粒子捕集的湍流捕集效应数值分析 [J]. 中国环境科学, 2013,33(9):1585-1590.

[13] Hosseini S A, Vahedi Tafreshi H. Modeling particle-loaded single fiber efficiency and fiber drag using ANSYS–Fluent CFD code [J]. Computers & Fluids, 2012,66:157-166.

[14] Longest P W, Vinchurkar S. Validating CFD predictions of respiratory aerosol deposition: Effects of upstream transition and turbulence [J]. Journal of Biomechanics, 2007,40:305-316.

[15] Geng T, Longest P W, et al. Development of a stochastic individual path (SIP) model for predicting the tracheobronchial deposition of pharmaceutical aerosols: Effects of transient inhalation and sampling the airways [J]. Journal of Aerosol Science, 2011,42:781-799.

[16] Wilcox D C. Reassessment of the scale-determining equation for advanced turbulence model [J]. AIAA Journal, 1988,26(11):1299-1310.

[17] Waldenmaier M. Measurements of inertial deposition of aerosol particles in regular arrays of spheres [J]. Journal of Aerosol Science, 1999,30(10):1281-1290.

[18] Ranz W E, Wong J B. Impaction of dust and smoke particles on surface and body collectors [J]. Industrial & Engineering Chemistry, 1952,44(6):1371-1380.

[19] Walton W, Woolcock A. The suppression of airborne dust by water spray [J]. International Journal of Air Pollution, 1960,3: 129-153.

[20] Schmidt M, Loffler F. Experimental investigations on two- phase flow past a sphere using digital Particle – image – velocimetry [J]. Experiments in Fluids, 1993,14(5):296-304.

[21] Langmuir I, Blodgett K B. Mathematical investigation of water droplet trajectories [J]. Atmospheric Phenomena, 1961,1062:335-347.

[22] Friedlander S K. Smoke, Dust, and Haze: Fundamentals of Aerosol Dynamics. Oxford University Press, USA, 2000, p71.

Influence of turbulent effect on the collection process of aerosols by raindrops.

HUA Feng-jiao, KANG Yan-ming*, ZHONG Ke
(School of Environmental Science and Engineering, Donghua University, Shanghai 201620, China). China Environmental Science, 2017,37(1)：13～20

To explore the influence of turbulent motion on collection efficiency, the collecting processes of different diameter aerosols captured by four diameter raindrops were estimated by employing numerical simulation with different turbulent intensities, respectively. Considering the characteristics of scavenging process in the turbulent flow field, the concept of collision probability was introduced to give the new definition of computational formula of collection efficiency in turbulent flow condition. On the basis of the concept, the influence of turbulent effect on the collection efficiency was discussed and analyzed. The numerical results show that the collision probability distributions for particle of different diameters are affected by background turbulent intensity. Furthermore, collection efficiency is strongly affected by turbulent intensity for dp≤ 5µm. The influence of turbulent effect on collection efficiency depends on the density and diameter of particle, which was independent of the raindrop diameter.

aerosol particle；raindrop；turbulent intensity；collection efficiency

X513,P426.6

A

1000-6923(2017)01-0013-08

华凤皎(1989-),女,山东烟台人,东华大学博士研究生,主要从事城市大气环境与室内空气品质研究.发表论文3篇.

2016-03-10

国家自然科学基金资助项目(41275157);上海市教委科研创新重点项目(14ZZ073)

* 责任作者, 教授, ymkang@dhu.edu.cn