层次维编码片段立方体生成算法应用研究
2017-02-22张子轩万定生
张子轩,万定生,朱 凯
(河海大学 计算机与信息学院,江苏 南京 210098)
层次维编码片段立方体生成算法应用研究
张子轩,万定生,朱 凯
(河海大学 计算机与信息学院,江苏 南京 210098)
数据量大、数据多维是水利普查数据的重要特征。根据水利普查决策分析的需要,在对数据立方体技术研究的基础上,基于部分物化策略,提出了建立层次维编码片段立方体(HDEFC)。利用维度属性的概念分层特性,在层次维片段中采用混合索引(B-tree和Bit Code)技术对每个层次维的层次属性进行二进制编码,再利用生成的维度编码代替原表中关键字,非层次维片段中采用倒排索引技术对每个片段子立方体进行物化,减少了多表连接操作,从而提高OLAP查询效率。实验结果表明,生成的HDEFC占用较小的存储空间,查询方法在面对高维的复杂查询时具有优势。通过建立水利普查数据分析系统,说明了该方法能够有效地解决因数据量庞大、维度多导致的数据计算和查询效率低下等问题,降低了物化水利普查成果数据立方体的时间和空间成本。
水利普查;数据多维;数据立方体;数据分析系统;层次维编码片段
0 引 言
随着全国水利普查[1]工作的开展,形成了迄今最为全面细致、完整系统的涉水基础数据资源和规范权威的水利普查成果数据,如何对这些普查成果数据进行有效的分析与利用成为了制定正确水利建设方案的关键问题。
数据仓库[2]作为一种新兴技术被越来越多的领域所重视,数据挖掘[3-4]和联机分析处理(OLAP)[5-6]都是基于数据仓库的分析工具。在OLAP中,数据通常以数据立方体(Data cube)[7]的方式存储,数据立方体以“维度+度量”的方式组织数据,提供给分析人员多维的数据视图,直观地支持了OLAP中所需要的复杂多维分析。为节省存储空间同时兼顾OLAP查询效率,对数据立方体进行预计算的有效方法可提高联机分析处理能力。
结合水利普查数据量大、多维度、分层次的特征,文中以建立层次维编码片段立方体(HDEFC)[8-9]为重心,采取能够有效处理高维度的HDEFC生成算法和查询算法,将其运用于水利普查数据分析,并逐步实现OLAP、数据挖掘等功能。以水利普查中的水电站工程数据分析主题为例,利用层次维编码片段立方体作为底层数据结构,并展开了对水利普查数据分析与展示系统的建立与应用研究。
1 层次维编码片段立方体技术
1.1 HDEFC思想
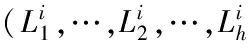

表1 水电站工程数据表
例1:表1生成的原始数据立方体由ADDVCD(水电站所在行政区划代码)、GCJB(水电站的工程级别)、JSQK(水电站建设情况)和KFFS(水电站开发方式)4个维度(简称A,G,J,K)和SL(数量)、ZJRL(水电站装机容量)2个度量构成,SK_Cube中包含16个聚集cuboids:{(A,G,J,K),(*,G,J,K),(A,*,J,K),(A,G,*,K),(A,G,J,*),(*,*,J,K),(*,G,*,K),(*,G,J,*),(A,*,*,K),(A,*,J,*),(A,G,*,*),(*,*,*,K),(*,*,J,*),(*,G,*,*),(A,*,*,*),(*,*,*,*)}。维度ADDVCD中包含3个概念分层以及4个不同的属性值,维度GCJB包含2个不同的属性值,维度JSQK包含2个不同的属性值,维度KFFS包含2个不同的属性值,则将生成32((3+1)×2×2×2)个聚集cuboids和810((4+1)×(2+1)×(1+1)×(2+1)×(2+1)×(2+1))个聚集单元。
以水利普查对象中的行政区划维ADDVCD为例,通过层次维编码方法创建Province(省份)、City(城市)和County(区县)这三个维度的层次编码,并将其与事实表中记录的TID进行关联。表1中ADDVCD维的编码与水电站工程数据简表中各记录的TID关联关系如表2所示。

表2 ADDVCD层次维编码表
定义3:层次维编码片段立方体。对于一个具有n个维度的高维数据立方体C(D,M),将维度集合{D1,D2,…,Dn}按照互不相交的原则,划分为k个独立的片段,其中层次维单独划分为一个片段,而非层次维划分为大小为m的片段。对层次维中的层次属性利用混合索引技术进行二进制编码,然后用倒排索引技术[10]存储非层次维片段中的聚集cuboids。这样就将一个n维的立方体分割成k个低维的立方体,形成HDEFC。
例2:以表1水电站工程数据简表为例,采用HDEFC生成算法,立方体片段大小为3,则划分出的HDEFC为(ADDVCD),(GCJB,JSQK,KFFS)共2个片段,需要物化12((3+1)+2×2×2)个聚集cuboids和57((4+1)×(2+1)×(1+1)+(2+1)×(2+1)×(2+1))个聚集单元,所需存储空间明显减少。
定义4:非层次维倒排索引。对于HDEFC立方体中每个非层次维的每个属性值,列出具有该值的所有元组的元组标识符(TID),形成非层次维的倒排索引。
例3:在表1中,非层次维有GCJB、JSQK、KFFS,对全部非层次维建立倒排索引。例如,属性值G1出现在元组1、2和3中,则G1的TID列表包含3项,即1、2和3。对这3个维中的属性值建立倒排索引得到表3。
至此,HDEFC立方体中层次维自成一个片段立方体,而非层次维片段立方体需要计算生成。表1中的非层次维恰好可以形成一个片段大小为3的立方体。

表3 由表1生成的非层次维倒排索引表
1.2 HDEFC生成算法
首先,将给定数据集(即基本方体)的所有维划分成独立的维群组,也可称作立方体片段。其中每个层次维单独为一个片段,数个非层次维组合成一个片段(关于非层次维的片段大小以及维分组将在下文进行讨论)。
扫描基本方体,并构造每个维属性的倒排索引。对于每个片段,计算完全局部(即基于片段的)数据立方体,而保留倒排索引。此外,对方体中每个单元保留倒排索引,即对于每个单元,记录它的关联TID列表。
算法伪代码如下所示:
输入:一个具有n个维度的立方体C:(D1,D2,…,Dn)。
输出:片段划分集合{F1,F2,…,Fk}和相对应的局部片段立方体{HC1,HC2,…,HCk};ID_measure数组。
方法:
将n维立方体C(D1,D2,…,Dn)分割成k个分段{F1,F2,…,Fk};
for(i=1;i<=n;i++){
将每个元祖的TID和MEASURE插入ID_measure数组;
if(维可分层){
利用二进制编码创建层次维编码表和TID关联表
}
else{
创建Di各属性TID关联表,即倒排索引
}
}
for(每个非层次维片段Fi){
交叉计算同一Fi片段中的Di维对应的TID列表值并计算其相应的度量值,创建局部片段立方体HCi;
}
1.3 HDEFC片段大小选择
HDEFC生成算法中,立方体片段大小的选择显得至关重要。片段过大会导致需要预聚集的立方体过多,从而增加存储空间的负担;片段过小会导致预聚集的立方体过少,从而无法满足大部分的临时聚集操作,增加响应时间。必须在存储空间和响应时间中寻找最佳平衡点,即HDEFC片段最佳大小。
根据HDEFC生成算法的思想,假设某立方体共有S个维度,片段大小为L,则每个片段将生成2L个立方体。将立方体片段大小L设为自变量x,因变量y为立方体总数量,得到函数(x>1)。
以水利普查中水库工程为例,维度总数为19(行政区划、流域水系、水资源区划、水库类型、挡水主坝类型按材料分、挡水主坝类型按结构分、主要泄洪建筑物形式、工程建设情况、水库调节性能、工程等别、主坝级别、重要保护对象、供水对象、水库归口管理部门、是否完成划界、是否完成确权、工程任务、2011年供水量数据来源、主要挡水建筑物类型),3个区域层次维自成片段,对剩下16个维度划分立方体片段。
经过研究得出,立方体数量随着立方体片段大小的增加呈指数级增长,即HDEFC存储空间与立方体片段大小呈指数关系。考虑到立方体片段过小造成的临时聚集时间增加这一可预见的事实,所以对于最佳立方体片段大小的选择应该是3或4为宜。
1.4 HDEFC查询算法
通常的查询类型包括点查询[11]、范围查询[6]和冰山查询[12]。由于HDEFC定位于水利普查高维数据查询,现在基于HDEFC结构模型,采用范围查询方法进行有效查询处理。
以范围查询为例,HDEFC范围查询算法可以被分解成多个点查询,在范围查询中,立方体至少存在一个维度di,其取值不唯一。该算法核心在于将查询条件中的维度条件分解整理后,找出同一HDEFC片段中的维度,分别从不同的HDEFC片段中查询出符合查询条件的TID列表,最终再对各TID列表进行求交。
详细的算法伪代码如下:
输入:立方体片段集合{HC1,HC2,…,HCk};ID_measure数组;
输出:基于范围查询的结果度量。
方法:
for(i=1;i<=k;i++){
Bqi←运用点查询算法得到每个点查询的相交集合;
}
if(存在至少一个非空Bqi){
Bq←{Bq1,Bq2,…,Bqk}集合求交得到最终集合;
}
M←Bq∩ID_Measure
returnM
2 实验结果与分析
本节在不同大小的数据集上对文中提出的HDEFC生成算法进行性能比较。实验硬件环境:处理器为Intel(R)Core(TM)i5-4750CPU@ 3.40GHz,内存为4GB,硬盘为640GB、7 200rpm。软件环境:操作系统为Win7,数据库为SQLServer2005,编程语言为Java,平台为Eclipse。
实验采用水利基本情况普查中的水电站工程对象数据,记录数为98 000,对基本表进行整理后选取18个维度属性和10个度量属性,并在实验前对各数据进行了规范化处理。各实验中每个片段大小为3。
图1是层次维编码相对简单位图索引的压缩比(坐标经过处理)。
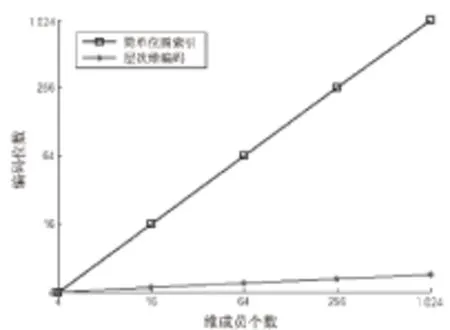
图1 层次维编码相对简单位图索引的压缩比
从图中可以看出,当维成员个数为256时,简单位图索引需要256bits,而层次维编码位数只需8bits,数据压缩比为256/8=32。随着维成员数量的持续增加,数据压缩比将进一步增大。
图2展示了基本事实表记录数对数据立方体存储空间的影响。

图2 存储性能比较
总的来说,HDEFC方法所需的存储空间整体小于简单原始的外壳片段立方体(Minimalcubing)[13-14]方法。随着记录数的增加,HDEFC方法中层次维编码高压缩性的特点就表现得更加明显,且所需存储空间的增长趋势相对缓慢。实验结果表明,HDEFC方法能够有效减少立方体存储空间,相对Minimalcubing方法具有一定优势。
3 系统设计与实现
依据文中所述的层次维编码片段立方体技术,系统进行了相应的数据库逻辑结构和物理结构设计。开发与部署主要运用了JSP和GROOVY技术,其中前台使用JSP技术进行界面展示,后台与SQLServer数据库的连接使用GROOVY语言,再结合ArcGIS平台对水利普查数据进行地图可视化展示。文中所构建的水利普查层次维编码片段数据立方体在系统运行过程中表现出显著的优势,比如对水利普查数据维度的分析与查询响应时间在该系统中得到了高效的实现,给用户带来了极大方便。图3显示了水利普查数据分析与展示信息结果。

图3 水利普查数据分析系统
该系统实现了水利普查成果展示、水利普查基础数据查询、水利普查主题查询、空间分布以及文档资料等功能,能够对水利普查数据进行查询与展示,可以有效地分析水利普查成果数据,进而进行决策分析。该系统运用信息可视化技术,建立了可交互的友好美观的用户界面,能有效地查询水利普查对象地理信息与具体信息。
水利普查数据分析系统还加入了“水利普查主题展示”的概念,在水利普查对象的大环境中以用户关注点为中心,进行单类对象多指标以及多类对象相关指标的主题定制展示。
总之,该系统的开发研究,为水利普查数据分析提供了有效的平台,以方便水利业务人员实现对于水利普查数据的二次加工和深度分析。
4 结束语
在介绍水利普查数据特征的基础上,文中提出了适用于高维水利普查数据分析的部分物化立方体结构—HDEFC,以具有代表性的水电站工程数据为例,就HDEFC的生成算法、查询算法和立方体片段大小选择进行了探究,并构建了水利普查数据分析系统。此系统能够满足对水利普查数据分析的基本要求,且数据分析查询响应速度快于一般数据仓库的多维数据分析系统。通过实验进一步验证了提出的HDEFC方法在水利普查数据分析领域的适用性。相比于目前数据分析系统中普遍采用的低维度少度量的处理方式,得益于HDEFC的底层立方体结构和相应的查询方式,可以灵活地进行高维度多度量的查询和分析,为水利决策者提供了更加广阔的数据视野。
[1] 庞进武,程益联,罗志东.水利普查与信息化[J].水利信息化,2012(1):19-22.
[2] 占 军,万定生,李 宇.基于Oracle数据仓库的水利普查数据展现系统[J].计算机与数字工程,2012,40(10):55-57.
[3] 杨嘉杰.水量水费数据立方体的OLAP和数据挖掘技术研究[D].广州:中山大学,2012.
[4] 尹 涛,关兴中,万定生.数据挖掘技术在水文数据分析中的应用[J].计算机工程与设计,2012,33(12):4721-4725.
[5]ChaudhuriS,DayalU.AnoverviewofdatawarehousingandOLAPtechnology[J].ACMSIGMODRecord,1997,26(1):65-74.
[6]HoCT,AgrawalR,MegiddoN,etal.RangequeriesinOLAPdatacubes[J].ACMSIGMODRecord,1970,26(2):73-88.
[7]GrayJ,ChaudhuriS,BosworthA,etal.Datacube:arelationalaggregationoperatorgeneralizinggroup-by,cross-tab,andsub-totals[J].DataMiningandKnowledgeDiscovery,1997,1:29-53.
[8]MarklV,RamsakF,BayerR.ImprovingOLAPperformancebymultidimensionalhierarchicalclustering[C]//ProcofIDEAS’99.[s.l.]:[s.n.],1999:165-177.
[9] 胡孔法,董逸生,徐立臻,等.一种基于维层次编码的OLAP聚集查询算法[J].计算机研究与发展,2004,41(4):608-614.
[10] 林俊鸿,姜 琨,杨岳湘.倒排索引查询处理技术[J].计算机工程与设计,2015,36(3):572-575.
[11] 朱 凯,万定生,程习锋.水利普查成果分析中数据立方体计算研究[J].计算机与数字工程,2014,42(9):1591-1594.
[12]FangM,ShivakumarN,Garcia-MolinaH,etal.Computingicebergqueriesefficiently[C]//Internationalconferenceonverylargedatabases.NewYork:[s.n.],1999.
[13]LiX,HanJ,GonzalezH.High-dimensionalOLAP:aminimalcubingapproach[C]//Proceedingsofthethirtiethinternationalconferenceonverylargedatabases.[s.l.]:[s.n.],2004:528-539.
[14]LiC,CongG,TungAKH,etal.Incrementalmaintenanceofquotientcubeformedian[C]//ProceedingsofthetenthACMSIGKDDinternationalconferenceonknowledgediscoveryanddatamining.Washington:ACM,2004:226-235.
Application Research on Hierarchical Dimension Encoding Fragment Cube Algorithm
ZHANG Zi-xuan,WAN Ding-sheng,ZHU Kai
(College of Computer and Information,Hohai University,Nanjing 210098,China)
Large amount of and multidimensional data is an important feature of water census data.According to the need of water census decision analysis,on the basis of data cube technology and partial materialization strategy,the establishment of Hierarchical Dimension Encoding Fragment Cube (HDEFC) is put forward.By the concept hierarchy characteristics of the dimension attribute,hybrid index (B-tree and Bit Code) technology is used to execute binary coding for hierarchy properties of each dimension,and the generated dimension code is applied to replace the key in the original table.In addition,non hierarchical dimension fragment uses inverted index technology to materialize each sub cube,so as to reduce the multi table join operation and improve OLAP query efficiency.Experiments show that the generated HDEFC occupies less storage space,and the query method has advantages in the face of high dimensional complex query.Through the establishment of water census data analysis system show that the method can effectively solve the problem of low efficiency of data calculation and query because of the huge amount of and multi-dimensional data,which reduces the cost of time and space of the material of water census results data cube.
water census;multi-dimensional data;data cube;data analysis system;hierarchical dimension encoding fragment
2016-04-08
2016-08-02
时间:2017-01-10
国家科技支撑计划课题(2015BAB07B01);水利部公益性行业科研专项(201501022)
张子轩(1994-),女,硕士研究生,研究方向为信息处理与信息系统;万定生,教授,CCF会员,研究方向为信息处理与信息系统。
http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1019.058.html
TP391
A
1673-629X(2017)02-0134-05
10.3969/j.issn.1673-629X.2017.02.030
