基于改进的均值漂移算法的运动汽车跟踪
2017-02-22孟晓琼
雷 飞,孟晓琼,吕 露,黄 涛
(北京工业大学 电子信息与控制工程学院,北京 100124)
基于改进的均值漂移算法的运动汽车跟踪
雷 飞,孟晓琼,吕 露,黄 涛
(北京工业大学 电子信息与控制工程学院,北京 100124)
交通领域的智能视频监控系统有效解决了车辆的实时跟踪问题。针对运动车辆的特点,提出一种均值漂移(Mean Shift)和粒子滤波相融合的跟踪算法。该算法以HSV颜色直方图为核心建立运动汽车目标模型,利用Bhattacharyya距离度量粒子区域和目标模型的相似性,并根据相似性来更新粒子权值。使用Mean Shift聚类偏移粒子,通过观测模型和再估计过程使得这些粒子的候选区域能更加接近真实的目标位置。实验结果表明,该算法具有较强的实时性和鲁棒性,能实现对感兴趣运动汽车的稳定跟踪。
均值漂移;粒子滤波;采样;目标跟踪
0 引 言
运动车辆跟踪是智能交通领域[1]的重要研究课题,对保障交通的有序运行具有重大意义。运动目标跟踪就是将一个连续视频序列转换成连续的图像序列,并从每帧画面中根据感兴趣的运动目标(例如车辆、行人、动物等)的位置、形状、色彩、纹理等相关特征对其进行实时定位,检测出运动目标的准确运动路径。传统的跟踪算法主要分为两种:一是传统的Mean Shift[2]目标跟踪算法,因其无需参数、计算量小,对目标变形、旋转变化适应性强等优点得到普遍应用和广泛研究。但是该算法在迭代过程中容易陷入局部最优解,造成目标跟丢现象。二是引入粒子滤波算法(PF)[3]。粒子滤波能够处理因为背景干扰、遮挡等问题带来的非线性和多模态的情景,可以实现并行化,跟踪鲁棒性较强,但算法的复杂度较高,很难满足多目标下的实时跟踪。
借鉴前人的研究经验,文中提出一种基于Mean Shift和粒子滤波相结合(MSPF)的运动汽车目标跟踪算法,并且融合了颜色和运动信息来建立目标描述模型,对传统的Mean Shift算法进行改进并将其嵌入到粒子滤波中,对粒子样本重新分配和传播[4],使其朝着目标状态的最大后验概率密度[5]的分布方向移动,以提高算法的跟踪效率。在充分描述目标状态的前提下,实现实时准确的目标跟踪。
1 颜色和运动信息的融合
信息提取流程如图1所示。

图1 颜色和运动信息的提取流程图
针对目标颜色特征[6]的尺度不变性和旋转不变性,结合基于HSV颜色空间的H和S两个分量来实现目标颜色概率分布图Ic(x,y)的创建。用运动概率分布图中目标区域内全部点的像素灰度值来计算目标的运动概率分布图Im(x,y)。设定搜索窗口为一个矩形区域,分别计算在颜色和运动两个概率分布图模型中该区域的对应零阶矩Mc和Mm,表示为:
(1)
利用表示颜色和运动信息的零阶矩[7],求解联合特征的零阶矩M,如式(2)所示:

(2)
其中,β∈[0,1]是融合概率,通常取β=0.8,反映了目标跟踪过程中颜色、信息等特征对跟踪结果的贡献度。
通过式(2)建立的融合机制[8],将两种概率分布图模型通过有选择性的加权结合于一体,得到更加可靠和稳定的目标模型。
2 基于颜色和运动信息融合的均值漂移算法
当目标出现在第一帧图像中时,用鼠标手动选取目标区域的初始位置,设为C0(x0,y0)。初始化迭代次数从0开始,改进的算法流程图如图2所示。
由图2可知,改进的基于颜色和运动信息的均值漂移算法的具体实现步骤如下:
Step1:由式(2)求出所选定跟踪的目标区域的零阶矩和一阶矩,有:
(3)

图2 改进的基于颜色和运动信息的均值漂移算法
其中,M00是融合的特征信息概率分布图中目标区域的零阶矩;M10和M01为分布图中目标区域的一阶矩。
Step2:根据M00、M10和M01,计算当前时刻的搜索区域的质心位置点(xc,yc),公式为:
(4)
Step3:计算当前的质心位置C1(xc,yc),并作为新的搜索窗口的中心。若‖C1-C0‖<ε或未达到迭代次数,将迭代次数加1,返回Step1重新计算新窗口的质心位置,直至迭代次数达到给定阈值或‖C1-C0‖≥ε为止,退出循环。
传统的教学模式非常机械,一般教师都是采用“满堂灌”的方法,不管学生是否能接受。这种教学模式在当今受到了很多业内人士的鄙视。小学是一个教育启蒙的阶段,而英语作为外来语言,在教学中,学生的自悟才是重点。因为兴趣是学生学习的推动力,所以要让学生喜欢英语和热爱英语。教师应该积极探索新的教学方式,敢于打破小学英语教学思维局限性,以增强小学生学习英语的积极性为考虑的第一前提。翻转课堂教学模式则是时代的产物,是目前最有效的英语教学方法之一,教师要合理应用该教学模式提高学生的学习效率。
3 基于改进的均值漂移算法的运动汽车跟踪
改进的跟踪算法如图3所示,分为三个部分:重采样过程、均值漂移过程、粒子观测和目标状态估计过程。
3.1 重采样过程
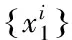

图3 基于均值漂移和粒子滤波相融合的算法原理
3.2 均值漂移过程
均值漂移过程充分体现了该算法基于均值漂移向量而对粒子产生的强烈聚合作用。采样粒子在经过重采样处理和状态转移模型传播后,粒子的位置产生了很大变化,使得很多粒子偏离了目标位置,所以用均值漂移算法对粒子进行聚类[11]收敛,使其朝目标状态的概率密度增长的方向聚集。具体步骤是:
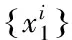

(5)

3.3 粒子观测和目标状态估计过程
粒子观测和目标状态估计过程中使用观测模型更新收敛后的粒子,利用权值变化后的粒子对目标状态进行估计。
(6)
采样粒子的权值满足:
(7)
由蒙特卡洛原理[14],通过粒子的加权求和得出目标状态的后验估计xk,满足等式:
(8)
因此,基于MSPF相结合实现的运动汽车跟踪的具体算法流程如图4所示。

图4 均值漂移和粒子滤波相融合的算法流程
4 实验结果及分析
仿真实验环境:四核处理器3.2GHz,4G内存,MicrosoftWindows7操作系统的台式机。运行环境是MATLAB,版本为7.14.0(R2012a)。
实验采用文中算法对运动汽车的视频进行目标跟踪,并与均值漂移算法下的跟踪效果进行比较,以验证文中算法的有效性。手动选取运动目标框图,用于跟踪的视频序列共351帧图像,图片尺寸为350×240,色彩深度为24位。

实验结果表明,采用粒子滤波算法实现汽车目标跟踪时,多次实验统计后要求粒子数量不能少于250,低于250则会出现目标跟丢的情况,而且算法读取连续帧序列的时间较长。对比之下,运用文中的MSPF融合算法只用了50个粒子就实现了较好的跟踪效果,如图5所示。在第5~50帧图像中,尽管目标相距摄像机较远,算法依旧实现了对其位置的准确识别和定位;在第75帧,目标在受到光线及阴影遮挡的情况下仍能定位到中心位置区域,随着运动目标的速度加大,融合算法始终保持了优秀的跟踪效果。

图5 基于融合算法的运动汽车跟踪结果
实验中分别运用三种算法对运动汽车跟踪时的运行时间进行了对比,其中融合算法下的运行时间稳定在100ms左右,且不会产生像均值漂移运行时间中突发的峰值情况。
5 结束语
文中提出了一种传统均值漂移与粒子滤波相融合的算法来实现运动汽车目标跟踪技术。实验结果表明,该算法保证了运动汽车跟踪的鲁棒性和实时性,排除了背景环境和目标特征因素的干扰,实现了快速而稳定的跟踪效果。但是文中只是针对单一目标实现跟踪而且需要手动选取目标跟踪区域,未来需要从多目标多模型的角度进一步开展工作。
[1] 吴 琳.计算机视觉导航综述[J].电脑知识与技术,2008(9):143.
[2]FukunagaK,HostetlerL.Theestimationofthegradientofadensityfunction,withapplicationsinpatternrecognition[J].IEEETransactionsonInformationTheory,1975,21(1):32-40.
[3]CollinsR.Asystemforvideosurveillanceandmonitoring:VSAMfinalreport[R].Pittsburgh:CarnegieMellonUniversity,2000.
[4]McKennaSJ,JabriS,DuricZ,etal.Trackinggroupsofpeople[J].ComputerVisionandImageUnderstanding,2000,80(1):42-56.
[5]ZivkovicZ.ImprovedadaptiveGaussianmixturemodelforbackgroundsubtraction[C]//Proceedingsofthe17thinternationalconferenceonpatternrecognition.Cambridge:[s.n.],2004:28-31.
[6] 赵增顺,沈继毕,王继贞,等.基于Bayes滤波的移动机器人定位方法[J].计算机科学,2011,38(2):199-201.
[7]HandschinJE.MonteCarlotechniquesforpredictionandfilteringofnon-linearstochasticprocesses[J].Automation,1970,6(4):555-563.
[8]IsardM,BlakeA.CONDENSATION-conditionaldensitypropagationforvisualtracking[J].InternationalJournalofComputerVision,1998,29(1):5-28.
[9] 刘文静,于金霞,汤永利.粒子滤波自适应部分系统重采样算法研究[J].计算机应用研究,2011,28(3):912-914.
[10]ParagiosN,DericheR.Geodesicactivecontoursandlevelsetsforthedetectionandtrackingofmovingobjects[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2001,22(3):266-280.
[11] 雷 飞,张新颖,王 依.基于均值漂移和粒子滤波相结合的水下运动目标跟踪[J].制造业自动化,2012,34(16):68-71.
[12] 张 虎,方 华,李春贵.基于改进混合高斯模型的自适应运动车辆检测算法[J].计算机应用与软件,2014,31(1):286-289.
[13]DellaertF,BurgardW,FoxD,etal.UsingtheCONDENSATIONalgorithmforrobust,Vision2basedmobilerobotlocalization[C]//ProceedingsoftheIEEEcomputersocietyconferenceoncomputervisionandpatternrecognition.LosAlantions,CA,USA:IEEEComputerSociety,1999:588-594.
[14] 王 鑫,胡昌华,暴飞虎.基于贝叶斯原理的粒子滤波算法[J].弹箭与制导学报,2006,26(2):269-271.
The intelligent video surveillance system effectively solves the problem of real-time tracking of vehicles in transportation field.According to vehicle characteristics,a new algorithm combined of Mean Shift and particle filter is proposed to track the target.The algorithm takes the HSV color histogram as the core to establish the target model of moving vehicle,using the Bhattacharyya distance to measure the similarity between particle region and the target model and updating the particle weights according to the similarity.After that,Mean Shift is used to cluster offset particles whose candidate region is closer to real target location through the observation model and re-estimation.Experimental results show that the algorithm has strong real-time performance and robustness,and can achieve the stable tracking of interest moving vehicles.
Mean Shift;particle filter;sampling;target tracking
2016-03-29
2016-08-02
时间:2017-01-10
北京市教育科技计划面上项目(KM201210005003)
雷 飞(1972-),男,副教授,研究方向为图像处理和实时控制;孟晓琼(1991-),女,硕士,研究方向为模式识别与图像处理。
http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1019.042.html
TP301
A
1673-629X(2017)02-0106-04
10.3969/j.issn.1673-629X.2017.02.024
Moving Vehicle Tracking Based on Improved Mean Shift LEI Fei,MENG Xiao-qiong,LYU Lu,HUANG Tao
(College of Electronic Information & Control Engineering,Beijing University of Technology, Beijing 100124,China)
