圆在生活中的应用

文/邓革周

圆在生活中的应用

文/邓革周

圆是初中数学的重要内容，其相关知识在生活中的应用广泛，现举数例加以说明.

一、足球射门问题

例1在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻．当甲带球冲到A点时，乙随后冲到B点，如图1所示，此时甲是自己直接射门好，还是迅速将球回传给乙，让乙射门好呢？为什么？（不考虑其他因素）

分析：谁射门好，关键看这两个点各自对球门MN的张角的大小，张角越大，射中的机会就越大．

解：迅速回传乙，让乙射门较好．在不考虑其他因素的情况下，如果两个点到球门的距离相差不大，要确定较好的射门位置，关键看这两个点各自对球门MN的张角的大小，张角越大，射中的机会就越大.

如图1所示，∠A＜∠MCN=∠B，即∠B＞∠A，也就是B处对MN的张角较大，在B处射中的机会要大些．

点评：本题考查同弧所对的圆周角相等的应用.

图1

二、扳手张开问题

例2如图2，正六边形的螺帽边长为a，这个扳手的开口b至少应是（用含a的代数式表示）（）

解：如图3，连接OC，OD，过点O作OH⊥CD于点H，则∠COD=60°，△OCD是等边三角形.

由等腰三角形三线合一可知，

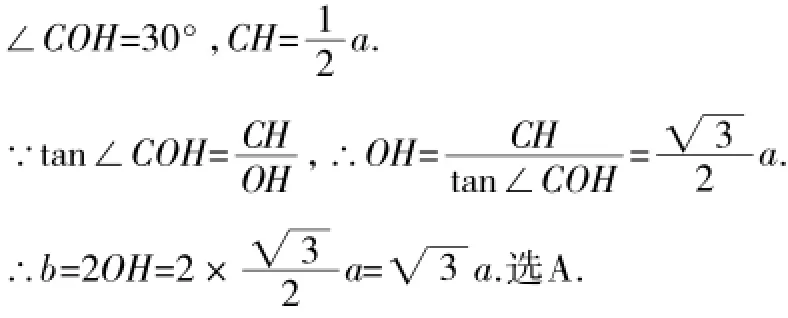
点评：本题考查正多边形和圆的知识，构造一个由半径、半条边、边心距组成的直角三角形，熟练运用锐角三角函数是解题的关键．

图2

图3

三、雨刷扫过的面积问题

例3当汽车在雨天行驶时，司机为了看清楚道路，要启动前方挡风玻璃上的雨刷器．图4是某汽车的一个雨刷器转动的示意图，雨刷器杆AB与雨刷CD在B处固定连接（不能转动），当杆AB绕A点转动90°时，雨刷CD扫过的面积如图4所示，现量得：CD=80cm，∠DBA=20°，AC=115cm，DA=35cm，试从以上信息中选择所需要的数据，求出雨刷扫过的面积．

解：由题意可知△ABD≌△AB′D′，△ACD≌△AC′D′，

大扇形半径AC=115cm，小扇形半径AD=35cm，且圆心角都为直角，所以雨刷CD扫过的面积为

图4

答：雨刷扫过的面积为3000πcm2．

点评：雨刷CD扫过的面积就是一个大扇形面积与小扇形面积的差，需分清楚哪些数据是有用的，哪些是没用的．根据扇形的面积公式计算．

四、车辆直角拐弯问题

例4车辆转弯时，能否顺利通过直角弯道的标准是：车辆是否可以行使到和路的边界夹角是45°的位置（如图5中②的位置），例如，图6是某巷子的俯视图（从上方往下看），巷子路面宽4m，转弯处为直角，车身为矩形ABCD，当CD与DE、CE的夹角都是45°时，连接EF，交CD于点G，若GF的长度至少能达到车身宽度，则车辆就能通过.

（1）试说明长8m，宽3m的消防车不能通过该直角弯；

（2）为了能使长8m，宽3m的消防车通过该弯道，可以将转弯处改为圆弧（分别是以O为圆心，以OM和ON为半径的弧），具体方案如图9，其中OM⊥OM′，请你求出ON的最小值．

图5

图6

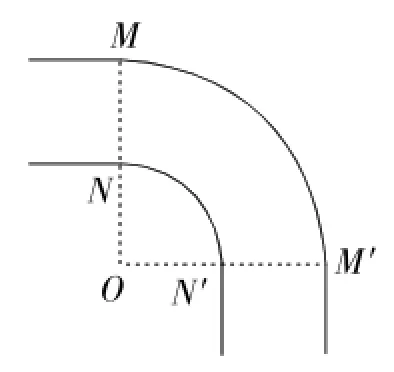
图7

图8

图9

解：（1）消防车不能通过该直角弯．

理由如下：如图8，作FH⊥EC，垂足为H，

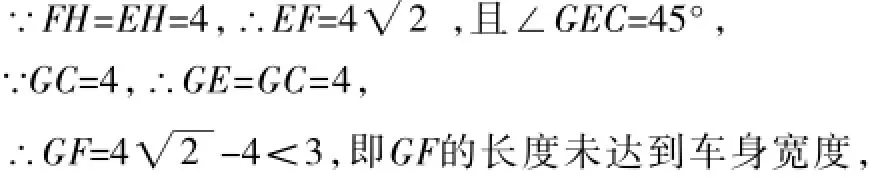
∴消防车不能通过该直角弯.

（2）如图9，若C、D分别与M′、M重合，则△OGM为等腰直角三角形，

设ON=x，连接OC，在Rt△OCG中，

OG=x+3，OC=x+4，CG=4，由勾股定理得OG2+CG2=OC2，

即（x+3）2+42=（x+4）2，解得x=4.5．

答：ON至少为4.5m．

点评：本题考查垂径定理的应用.把实际问题转化为数学问题并构造出等腰直角三角形是解题的关键．

五、井盖直径测量问题

例5如图10，现需测量一井盖（圆形）的直径，但只有一把角尺（尺的两边互相垂直，一边有刻度，且两边长度都长于井盖半径）．请配合图形，用文字说明测量方案，写出测量步骤．（要求写出两种测量方案）

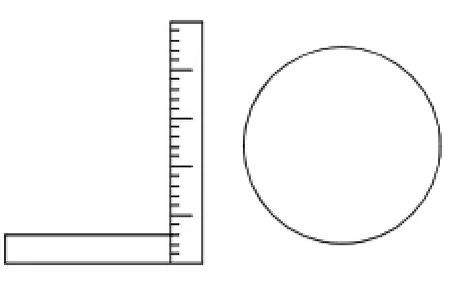
图10

图11

解：解法一：如图11（1），把井盖卡在角尺间，可测得AB的长度，记井盖所在圆的圆心为O，连接OB、OC，由切线的性质得OB⊥AB，OC⊥AC，又AB⊥AC，OB=OC，则四边形ABOC为正方形，那么井盖半径OC=AB，这样就可求出井盖的直径，直径为2AB.

解法二：如图11（2），把角尺顶点A放在井盖边缘，记角尺一边与井盖边缘交于点B，另一边交于点C（若角尺另一边无法达到井盖的边上，把角尺当直尺用，延长另一边与井盖边缘交于点C，度量BC的长即为直径.

解法三：如图11（3），把角尺当直尺用，量出AB的长度，取AB中点C，把角尺顶点与C点重合，一边与CB重合，让另一边与井盖边缘交于D点，延长DC交井盖边缘于E，度量DE长度即为直径.

解法四：如图11（4），把井盖卡在角尺间，记录B、C的位置，把角尺当作直尺用，可测得BC的长度.记圆心为O，作OD⊥BC，D为垂足，由垂径定理得BD=DC=BC，且∠BOD=∠COD.由作图知∠BOC=90°，∴∠BOD=×90°=45°，在Rt△BOD中，BO=，这样就可求出井盖的半径，进而求得直径.

点评：这是一个方案设计的开放性问题，综合性强，设计方法灵活，要充分利用所给工具的特征，并结合圆的相关知识选择测量方法.