轴力对混凝土管片极限承载力影响的计算模型
2017-02-21李守巨刘军豪
李守巨,于 申,刘军豪
(大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)
轴力对混凝土管片极限承载力影响的计算模型
李守巨,于 申,刘军豪
(大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)
针对混凝土管片受压区高度小和受压区钢筋未达到屈服极限问题,提出了混凝土管片极限承载力计算模型。在轴力和弯矩共同作用下,将混凝土管片简化为偏心受压柱,建立了管片截面力平衡和弯矩平衡表达式。基于管片截面平面变形假定,建立了受压区钢筋应力与受压区高度和混凝土极限应变之间的关系。通过2个地铁隧道管片工程算例,分析讨论了轴力对受压区高度、受压区钢筋应力和管片极限承载力的影响。研究表明,混凝土管片的极限弯矩随着轴力的增加而增加;混凝土管片的最不利荷载组合为最大弯矩与最小轴力的组合。混凝土管片受压区的钢筋往往没有达到屈服极限,有时甚至处于受拉状态;现有模型假设受压区的钢筋屈服与钢筋的实际应力状态差异较大,新的计算模型能够准确计算受压区的钢筋的应力。
偏心受压;混凝土管片;极限承载力;计算模型;受压区高度;钢筋应力
钢筋混凝土管片是地铁隧道、水工隧洞、矿山竖井和巷道等地下工程的常见衬砌结构。混凝土管片优化设计和准确极限承载力分析是保证地下结构安全性和经济性的重要研究内容之一。在混凝土管片的优化设计方面已有很多专家学者进行了多方位的研究。Moller等分析了隧道施工过程中不同的安装步骤对地表沉降和衬砌力的影响[1];Caratelli等研究了在隧道建设中用纤维增强预制混凝土代替传统钢筋混凝土的可行性[2];Jiang等对预制混凝土桥梁尽心研究,得出混合筋段有良好的延性和抗弯性能[3];Shalabi等对隧道管片的防漏性能进行了研究[4];Yan等比较分析了多种防火隧道衬砌管片,得出抗弯加固和使用混合纤维的钢筋混凝土设计即有良好的抗剥落性,又有足够的结构强度[5];Zhang等通过一种简单实用的方法对液氮注入岩石的渗透性进行了数值模拟[6];Sun等对高应力软岩巷道的支护技术进行了研究[7];Xue等分析了巷道覆盖层位移场和应力场的演化规律,并分析了裂缝的动态发展过程和分布规律[8]。对于管片力学性能的研究,特别是随着盾构机等机械掘进设备的广范应用,已引起了国内外学者的普遍关注。Zhang等和Arnau等分别研究了螺栓之间和管片相邻环之间的相互作用[9-10];Do等建立了二维有限差分模型,研究了侧向土压力系数和隧道周边土体的性质等因素对隧道衬砌管片的力学影响[11];Ye等对不同荷载不同螺栓预紧力和不同装配方式下的横向抗弯刚度进行了研究[12];Nehdim等对隧道衬砌管片中超高性能纤维增强混凝土的力学性能进行了试验研究[13];毕湘利等对通缝拼装和内张钢圈加固盾构隧道结构进行了极限承载力足尺试验研究[14-15]。目前对盾构隧道管片的极限承载能力以原型试验和理论分析相结合,因此,建立准确的理论模型对隧道管片的力学性能评估是至关重要。
本文通过研究混凝土管片的极限弯矩与轴力之间的关系,分析受压区钢筋真实的应力状态,探讨混凝土管片的最不利荷载组合,进一步完善混凝土管片极限承载力模型。
1 混凝土管片极限承载力现有计算模型
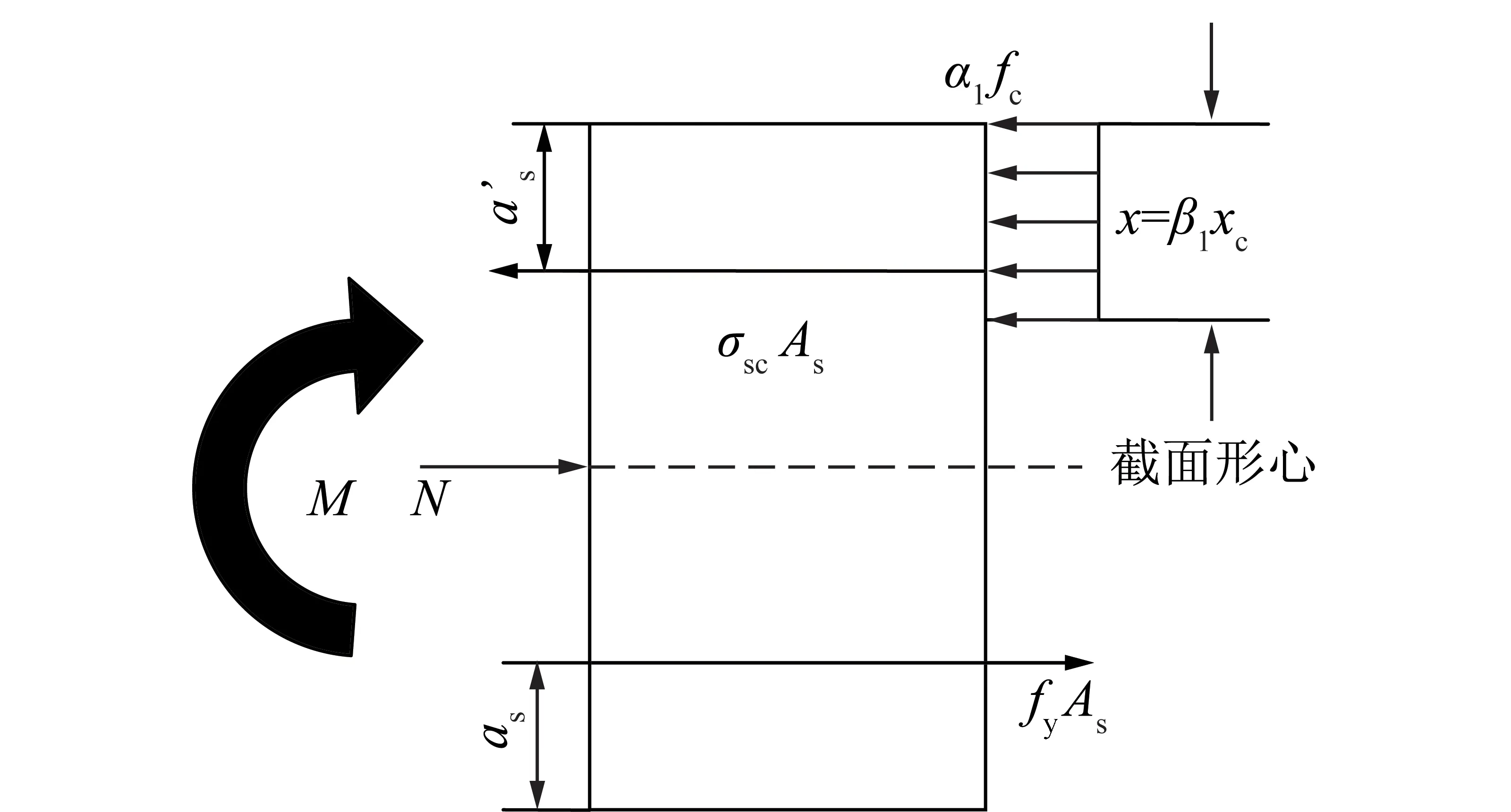
将对称配筋的混凝土管片简化为偏心受压模型,按照现行的钢筋混凝土设计规范,假设混凝土管片受拉区和受压区钢筋屈服,如图1所示。

图1 对称布筋混凝土管片受力分析简图
假设管片截面所受的轴力N的设计值已知,混凝土的标号已知,并且对称配筋的钢筋面积已知,根据力的平衡和弯矩平衡关系,计算管片的极限弯矩。由图1截面力的平衡条件得到
式中,α1为系数,与混凝土的强度等级有关;fc为混凝土的轴心抗压强度设计值;b为管片宽度;x为受压区高度。式(1)可表示为
轴力作用点至受拉钢筋中心之间的距离为
式中,h0为截面的有效高度;as为受拉钢筋中心到受拉边缘的距离;fy和As分别为为受拉钢筋的屈服强度和截面面积。截面的初始偏心距为
式中,h为管片高度。截面计算偏心距为
式中,ea为截面附加偏心距。基于混凝土结构设计规范,混凝土管片的极限弯矩为
基于混凝土结构设计规范,判断管片柱子模型是否大偏心受压判据为
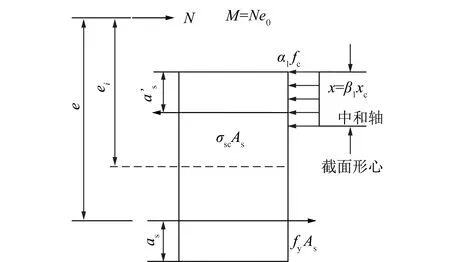
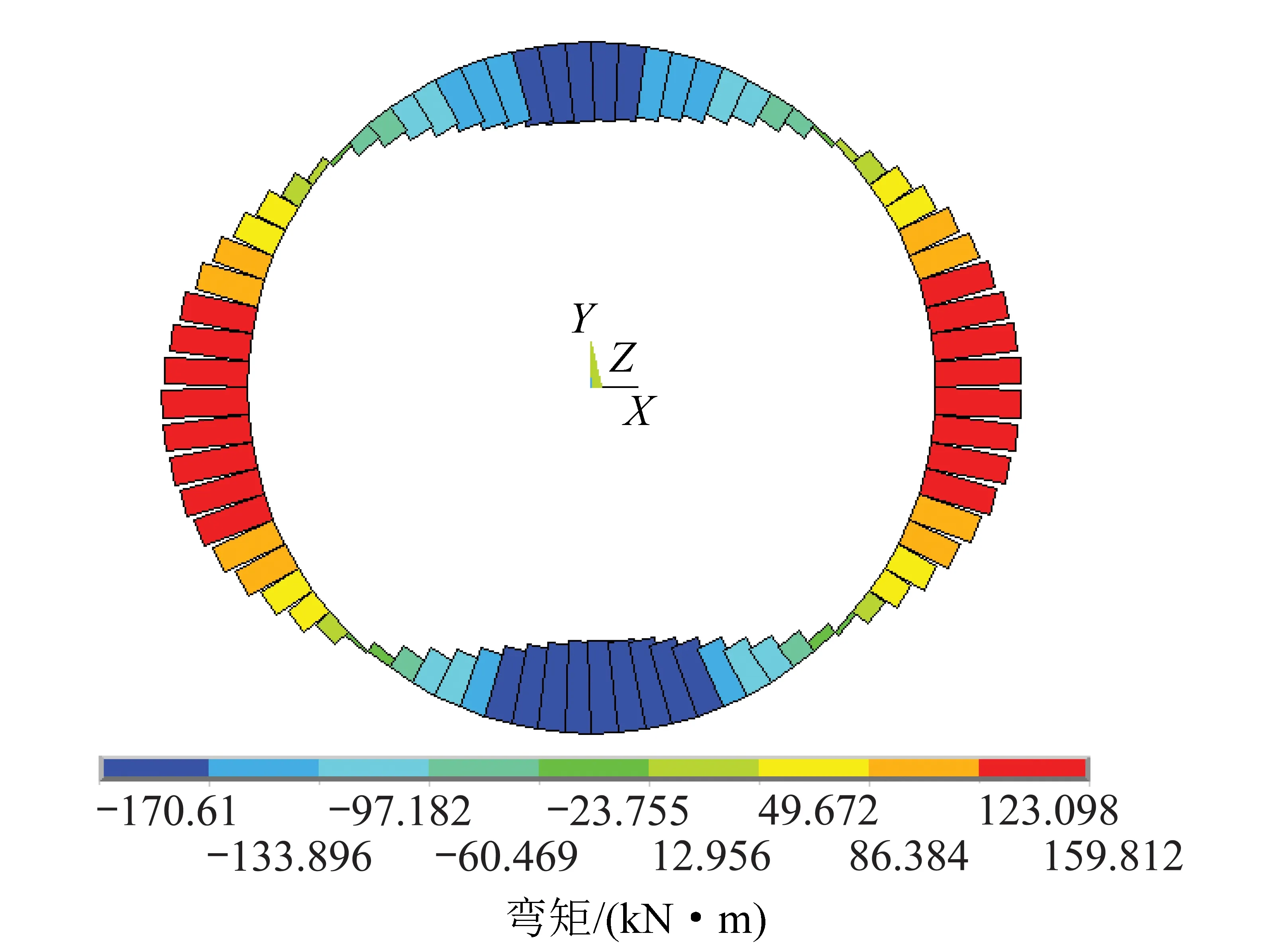
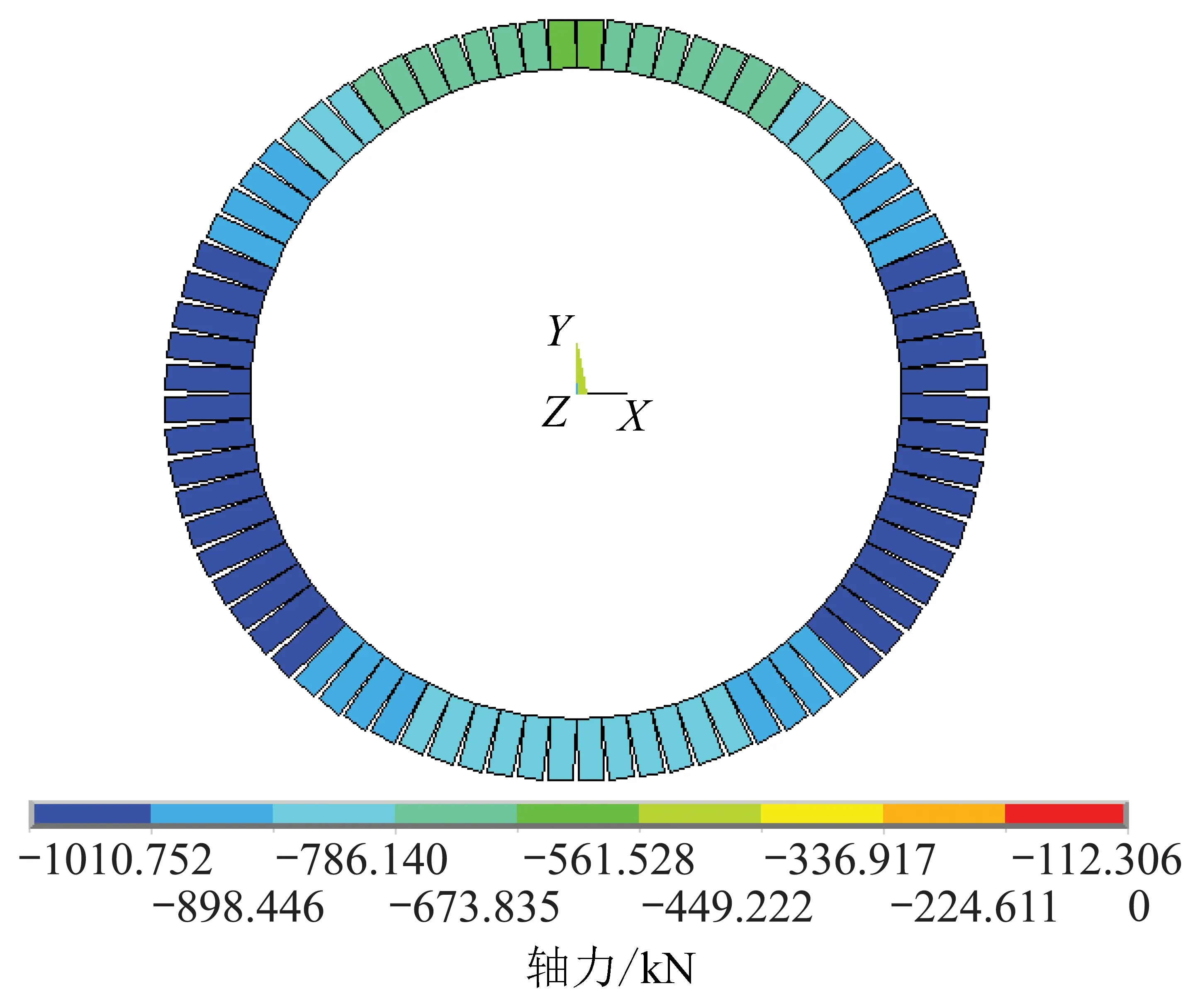
式中,Nub为界限情况下受压承载力设计值;xb为混凝土的界限受压区高度。当N 式中,ξb为混凝土的相对界限受压区高度 混凝土管片极限承载力的计算步骤为:① 根据式(7)判断,管片是否为大偏心受压构件;② 由式(2)计算管片受压区高度;③ 根据式(5)计算轴力对截面重心的偏心距;④ 根据式(6)计算混凝土管片的极限弯矩。 考虑到地铁隧道混凝土结构的特殊性,混凝土的标号较高,经常采用C50或者C55,甚至C60混凝土,并且管片截面高度远小于截面宽度,使得混凝土管片受压区的高度较小,往往混凝土管片受压区的钢筋没有达到屈服(图2),甚至所谓的受压区钢筋可能处于受拉状态。在此情况下,现有模型计算所得到的受压区钢筋应力与实际的受力状态差别较大,如果按照现有模型进行管片设计和承载力复核可能会带来一些问题。 根据图3,由截面力的平衡条件得到 式中,σsc为受压钢筋的应力;可得 假设受压钢筋没有达到屈服极限,钢筋应力与应变的关系为 图2 管片简化为偏心受压柱模型受力分析简图 图3 对称布筋大偏心管片承载力计算简图 图4 简化混凝土管片应变分布 在偏心轴力N作用下,根据梁平截面变形假定和应变三角形相似关系(图4),受压区钢筋应变与混凝土极限压应变的关系为 式中,εcu为混凝土的极限压应变,一般取εcu=0.003 3,对于C50以下的混凝土,β1=0.8;as为受拉钢筋的合力点至截面受拉边缘的竖向距离,一般取为as=40 mm。xc为中和轴高度,即受压区的理论高度;x为矩形应力图受压区高度。εsc为受压区钢筋的应变,当εsc<0时,表示受压区钢筋处于受拉状态,受压区的理论高度小于钢筋形心到混凝土管片表面的距离;否则,当εsc>0时,表示受压区钢筋处于受压状态。 将式(14)代入式(12),得 将式(15)代入式(11),得 由式(17)求出受压区高度x,然后代入到式(15),求出受压钢筋的应力。根据图3力矩平衡关系,得 e0=e-h/2+as-ea= 在式(17)求出出受压区高度x,式(15)受压钢筋的应力和式(20)求出e0基础上,基于混凝土结构设计规范,混凝土管片的极限弯矩为 Mu=Ne0=α1fcxb(h0-0.5x)+ 混凝土管片极限承载力新模型的计算步骤为:① 根据式(7)判断,管片是否为大偏心受压构件;② 由式(17)计算管片受压区高度;③ 由式(15)计算受压区钢筋的应力;④ 根据式(20)计算轴力对截面重心的偏心距;⑤ 根据式(21)计算混凝土管片的极限弯矩。 为了研究新的计算模型与现有计算模型的差异,通过两个盾构施工的地铁隧道实例,研究盾构隧道管片的极限承载力和受压区钢筋受力特性,讨论现有计算模型所存在的缺陷。 算例1为北京地铁10号线盾构隧道某断面[16],隧道管片外径6.0m,管片衬砌中心半径2.85m,管片厚度0.3m,管片宽度为1.2m,覆土厚度10.31m,覆土容重18.82kN/m3。混凝土管片强度等级为C50,采用对称配筋,管片主筋采用HRB335钢筋,as=40 mm,单侧主筋面积As=2 514 mm2(8φ20)。 采用有限元方法得到混凝土管片内力分布如图5和6所示。其中,最大正弯矩160 kN·m,最大负弯矩170 kN·m,轴力处于受压状态,其数值在400~1 010 kN之间变化。采用现有方法和改进模型计算管片极限弯矩随轴力的变化见表1和2。 图5 北京地铁混凝土管片弯矩分布 图6 北京地铁混凝土管片轴力分布 表1 管片极限弯矩随轴力的变化(现有方法,北京地铁) Table 1 Variation of bending moment of segments versus axial force (Current model,Beijing Metro) 轴力/kN4005006007008009001000x/mm14.418.121.625.2528.832.536.1Mu/(kN·m)215226237248258268278σsc/MPa300300300300300300300 表2 管片极限弯矩随轴力的变化(修改模型,北京地铁) Table 2 Variation of bending moment of segments versus axial force (New model,Beijing Metro) 轴力/kN4005006007008009001000x/mm35.637.038.640.241.943.645.5Mu/(kN·m)224233242251260269278σsc/MPa6690113134156176196 从图7中可以看出,混凝土管片的受压区高度随轴力的增加而增加,修改后模型的受压区高度大于现有模型计算结果。其原因在于,现有模型假设受压区钢筋达到屈服强度,导致与轴力相平衡的受压区高度减少。 图7 受压区高度随轴力的变化 从图8中可以看出,混凝土管片的受压区钢筋应力随轴力的增加而增加。现有模型假设受压区钢筋 图8 受压区钢筋应力随轴力的变化 应力达到屈服,而准确的计算发现,受压区钢筋远远没有达到受压屈服强度,对于东莞隧道,受压区钢筋却基本处于受拉状态。 从图9中可以看出,尽管2种计算模型所得到的受压区高度和受压区钢筋应力差异较大,但是管片的极限承载力却基本相同,这也可能是按照现有方法设计管片未出现大的工程事故的原因之一。 图9 管片极限承载力随轴力的变化 算例2为东莞至惠州城际轨道交通工程某穿越东江水下隧道[17],全长为2 998.276 m,过江段设计最高水位16.2 m,最低水位9.74 m,最大埋深16.2 m,最小埋深14.11 m。区间隧道衬砌管片外径8.5 m,内径7.7 m,管片环宽度1.6 m,厚度400 mm。管片采用C50混凝土,采用对称配筋,管片主筋采用HRB335钢筋,as=40 mm,单侧主筋面积As=882 mm2。文献[1]计算得到的最大弯矩90 kN·m左右,最大轴力1 000 kN左右。东莞隧道管片极限弯矩随轴力的变化见表3和4所示。 表3 管片极限弯矩随轴力的变化(现有模型,东莞隧道) Table 3 Variation of bending moment of segments versus axial force (Current model,Dongguan tunnel) 轴力/kN4005006007008009001000x/mm10.813.516.218.921.624.427.0Mu/(kN·m)154171188204220235253σsc/MPa300300300300300300300 表4 管片极限弯矩随轴力的变化(修改模型,东莞隧道) Table 4 Variation of bending moment of segments versus axial force (New model,Dongguan tunnel) 轴力/kN4005006007008009001000x/mm23.625.026.628.230.031.633.5Mu/(kN·m)165180195209224239251σsc/MPa-235-182-134-88-46730 注:钢筋应力负数表示受压区钢筋应力为受拉状态。 (1)混凝土管片受压区钢筋往往没有达到屈服强度,有时甚至处于受拉状态,按照现有模型假设受压区钢筋达到屈服应力进行管片设计,与钢筋实际受力状态差异较大,尽管两种模型得到的管片极限弯矩差别不大。 (2)从两个工程实例的计算结果可以看出,混凝土管片的极限承载力随着轴力的增加而增加。采用最大弯矩与最大轴力组合设计管片是存在某些问题的,实际管片最不利荷载组合应该是最大弯矩与最小轴力组合。 (3)计算结果表明,混凝土管片受压区高度随着管片轴力的增加而增加,受压区高度最大值远远没有达到2as;也就是说,无法保证受压区钢筋达到屈服极限。 (4)在大埋深和高水压条件下,例如琼州海峡海底隧道,埋深50~80 m,水深70~100 m,管片的轴力将显著增加,管片可能处于小偏心受压状态,如何针对此类问题提出计算模型需要进一步研究。 [1] Moller S C,Vermeer P A.On numerical simulation of tunnel installation[J].Tunnelling & Underground Space Technology,2008,23(4):461-475. [2] Caratelli A,Meda A,Rinaldi Z,et al.Structural behaviour of precast tunnel segments in fiber reinforced concrete[J].Tunnelling & Underground Space Technology,2011,26(2):284-291. [3] Jiang H,Cao Q,Liu A,et al.Flexural behavior of precast concrete segmental beams with hybrid tendons and dry joints[J].Construction & Building Materials,2016,110:1-7. [4] Shalabi F I,Cording E J,Paul S L.Concrete segment tunnel lining sealant performance under earthquake loading[J].Tunnelling & Underground Space Technology,2012,31(5):51-60. [5] Yan Z G,Shen Y,Zhu H H,et al.Experimental investigation of reinforced concrete and hybrid fibre reinforced concrete shield tunnel segments subjected to elevated temperature[J].Fire Safety Journal,2015,71(3):86-99. [6] Zhang C H,Wang L G,Du J H,et al.Numerical modelling rock deformation subject to nitrogen cooling to study permeability evolution[J].International Journal of Coal Science & Technology,2015,2(4):1-6. [7] Sun L H,Wu H Y,Yang B S,et al.Support failure of a high-stress soft-rock roadway in deep coal mine and the equalized yielding support technology:a case study[J].International Journal of Coal Science & Technology,2015,2(4):279-286. [8] Xue J H,Wang H P,Zhou W,et al.Experimental research on overlying strata movement and fracture evolution in pillarless stress-relief mining[J].International Journal of Coal Science & Technology,2015,2(1):38-45. [9] Zhang W,Koizumi A.A study of the localized bearing capacity of reinforced concrete K-segment[J].Tunnelling & Underground Space Technology,2007,22(4):467-473. [10] Arnau O,Molins C.Three dimensional structural response of segmental tunnel linings[J].Engineering Structures,2012,44(6):210-221. [11] Do N A,Dias D,Oreste P,et al.2D numerical investigation of segmental tunnel lining behavior[J].Tunnelling & Underground Space Technology,2013,37(6):115-127. [12] Ye F,Gou C F,Sun H D,et al.Model test study on effective ratio of segment transverse bending rigidity of shield tunnel[J].Tunnelling & Underground Space Technology,2014,41(1):193-205. [13] Nehdi M L,Abbas S,Soliman A M.Exploratory study of ultra-high performance fiber reinforced concrete tunnel lining segments with varying steel fiber lengths and dosages[J].Engineering Structures,2015,101:733-742. [14] 毕湘利,柳献,王秀志,等.通缝拼装盾构隧道结构极限承载力的足尺试验研究[J].土木工程学报,2014,47(10):117-127. Bi Xiangli,Liu Xian,Wang Xiuzhi,et al.Experimental investigation on the ultimate bearing capacity of continuous-jointed segmental tunnel linings[J].China Civil Engineering Journal,2014,47(10):117-127. [15] 毕湘利,柳献,王秀志,等.内张钢圈加固盾构隧道结构极限承载力的足尺试验研究[J].土木工程学报,2014,47(11):128-137. Bi Xiangli,Liu Xian,Wang Xiuzhi,et al.Experimental study on the ultimate load-bearing capacity of deformed segmental tunnel linings strengthened by steel plates[J].China Civil Engineering Journal,2014,47(11):128-137. [16] 陈丹.北京地铁盾构隧道管片设计方法比较[J].铁道标准设计,2009(10):60-64. Chen Dan.Comparative analysis of designing methods of tunnel segments for Beijing Metro[J].Railway Standard Design,2009(10):60-64. [17] 胡辉,张列,仇文革.三种盾构管片配筋设计方法对比及现场实测分析,2012,39(6):72-76. Hu Hui,Zhang Lie,Qiu Wenge.Comparative analysis of three kinds of designing methods of tunnel segments and field experiment investigation[J].Hydrogeology and Engineering Geology,2012,39(6):72-76. Computing model for influence of axial force on ultimate bearing performance of concrete segments LI Shou-ju,YU Shen,LIU Jun-hao (StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,China) Taking into account the problems of small compressive depth and less than yielding strength for bars located in the compressive zone of concrete segments,a new computing model is proposed to evaluate the ultimate bearing performance of concrete segments.Under the actions of both axial force and bending moment,the concrete segment is simplified to column with eccentric compressive loading,and the expressions for force balance and bending moment balance are derived.Based on the plane deformation assumption,the relationships between the stress of reinforced bars in the compressive zone and compressive depth in the concrete segment are proposed.Through two practical examples of underground tunnels lined by concrete segments,the influences of the axial force on compressive depth,the stress of reinforced bars and ultimate bearing performances of concrete segments are investigated.The computing results show that the ultimate bending moment of concrete segment increases with the increase of axial force,and the worst loading combination is the maximum bending moment with minimum axial force.The stress of reinforced bars in compressive zone cannot reach the yielding limit of material and are even in tensile state in some loading cases.The difference between the assuming stress and practical stress for existing model is obvious.The proposed computing model can precisely calculate the stress of reinforced bars in the compressive zone. eccentric compressive loading;concrete segment;ultimate bearing performance;computing model;compressive depth;bar stress 10.13225/j.cnki.jccs.2016.0403 2016-03-31 2016-07-15责任编辑:常 琛 国家重点基础研究发展计划资助项目(2015CB057804);国家自然科学基金资助项目(11572079);工业装备结构分析国家重点实验室开放基金资助项目(S14206) 李守巨(1960—),男,辽宁沈阳人,教授,博士。E-mail:lishouju@dlut.edu.cn TU528 A 0253-9993(2017)01-0236-06 李守巨,于申,刘军豪.轴力对混凝土管片极限承载力影响的计算模型[J].煤炭学报,2017,42(1):236-241. Li Shouju,Yu Shen,Liu Junhao.Computing model for influence of axial force on ultimate bearing performance of concrete segments[J].Journal of China Coal Society,2017,42(1):236-241.doi:10.13225/j.cnki.jccs.2016.04032 混凝土管片极限承载力新的计算模型

3 数值算例


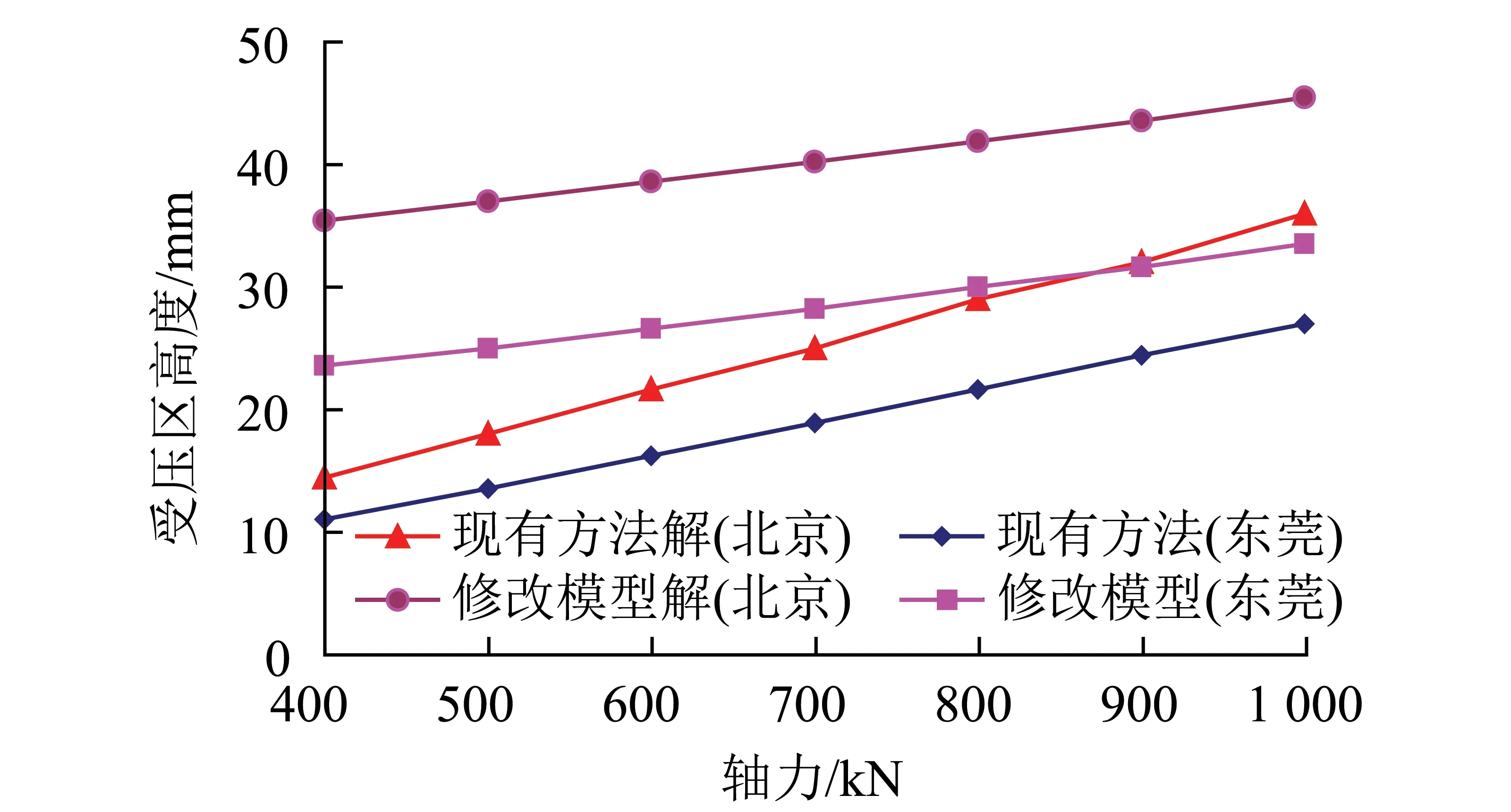
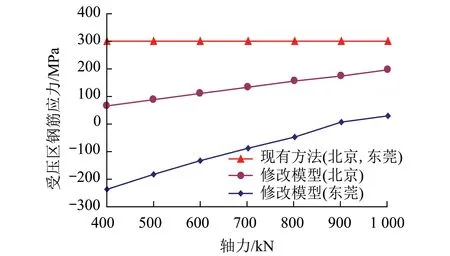



4 结 论
