基于模拟退火算法的应急物流车辆调度

唐冲

（军事交通学院 学员旅，天津 300161）

基于模拟退火算法的应急物流车辆调度

唐冲

（军事交通学院 学员旅，天津 300161）

根据应急物流的突出特点，对应急物流车辆调度路径优化进行了探讨。建立了基于有单边时间窗的应急物流车辆调度问题的数学模型，并针对该数学模型，设计了与其相适应的模拟退火算法。从实例计算结果看，该算法简单可行，计算效率高，收敛速度快,对于加快物资投送，处理好突发事件具有重要意义。

模拟退火算法；应急物流；车辆调度

1 引言

近年来，自然灾害、公共卫生和社会安全事件在我国发生的频率越来越高，对社会的发展进步造成了严重威胁。所谓应急物流即是指以提供自然灾害、公共卫生、社会动乱等突发事件所需应急物资为目的，以追求时间效益最大化和灾害损失最小化为目标的特种物流活动[1]。因此，如何处理好应急物流的车辆路径问题（VRP,Vehicle Rooting Problem）,成为减小突发事件带来损失的关键。

解决应急物流VRP的方法通常包括精确算法和启发式算法。其中，精确算法由于其计算量随问题规模的增大呈指数增长，实际应用范围受限[2]。而在启发式算法中，模拟退火算法（SAA,Simulated Annealing Algorithm）以其收敛速度快、计算效率高的特点得到广泛应用。

SAA最早的思想由N.Metropolis于1953年提出，1983年S.Kirkpatrick成功将退火思想引入到组合优化领域[3]，为解决应急物流VRP提供了新的思路。但大部分研究，仅停留在解决无时限的VRP上，对于将SAA应用于有时限的VRP的研究却很少。本文基于SAA，解决了有单边时间窗的应急物流配送的车辆调度问题，得到了较好的计算结果。

2 单边时间窗VRP模型

2.1 问题描述

为使问题易于理解，引入一个有单边时间窗的配送车辆调度问题。在该问题中，所有节点及其配送中心之间都有线路连通，且各节点物资需求量一定，所有运输车辆皆在0时刻出发，物资到达的单边时间窗一定，要求合理安排运输车辆，使得总的运输距离最小。该问题满足以下约束条件：(1)每个节点的物资需求量必须得到满足，且只能由一台车辆完成该节点的物资运送；(2)物资必须在允许的单边时间窗内到达节点；(3)车辆不允许超载。

某地发生地震灾害，现有n个受灾节点需要物资配送，某汽车部队立即出动，准备将驻地救灾物资运往受灾节点，驻地共有运输车为K辆，载重量为Q,第i个受灾节点的物资需求量为gi(i=0,1,···,n),驻地到各节点的距离为d0i(i=0,1,···,n),运输时间为t0i(i=0,1,···,n),各节点间的距离为 dij(i,j=0,1,···,n),运输时间为tij(i,j=0,1,···,n),每吨货物的卸货时间为ta,货物需要在[0,ai]内运到i节点。

2.2 模型建立

通过分析上述条件，可得相邻两节点之间的物资达到时间满足：

根据各节点物资需求量及单车运载量，确定路径条数（所需车辆数）：

为方便模型建立，定义两个0,1变量：

建立该单边时间窗的配送车辆调度模型：

在上述模型中，(1)式为模型的目标函数，要求最短运送距离最短；(2)式表示运送路径数应小于车辆总数；(3)式表示车辆k只能驶入安排其运送的节点；(4)式表示车辆k只能驶出安排其运送的节点；(5)式表示某节点只能由一辆车运送物资；(6)式表示车辆应在预定时间到达节点；(7)式表示运送路径k上所有节点的物资总需求量应小于车辆的载重量。

3 单边时间窗VRP的模拟退火算法

3.1 模拟退火算法的原理

SAA是基于Monte-Carlo迭代求解法，并利用一般组合优化问题与金属退火原理的相似性建立的一种随机搜索算法。金属在被加热至充分高，然后冷却的过程中，内部粒子由无序逐渐变为有序，且在每个温度趋于能量最低态的概率为exp(-ΔE/kT)，E为温度T时金属的内能，k为玻尔兹曼常数。利用这一退火特性，当邻域的一个解使得目标函数减小时，便接受这个解作为新的当前解，相反，SAA以的概率接受相对更差的解作为当前解，Δf为前后两次目标函数的差值。这种具有概率突跳性的Metropolis搜索准则有效地跳出了陷入局部最优的瓶颈，从而达到全局最优。其实现步骤如图1所示。

图1 SAA算法流程图

其中，n(Tk)为提前设定的内循环次数，Tf为外循环终止温度，T0为初始温度，n为温度Tk下内循环迭代步数，k为外循环降温的次数。

3.2 单边时间窗VRP的模拟退火算法设计

将单边时间窗VRP与SAA对比可知，单边时间窗VRP的解对应退火金属的状态，目标函数对应退火过程中金属的能量，而最优解则对应金属退火中的最低能量状态。为此，可以很好地将SAA运用于单边时间窗VRP的求解中。

（1）解的评价指标。解的评价指标是取得最优解的重要保证，为了将模型中不满足时间，运量约束以及路径数大于车辆数的解排除，引入惩罚因子P（根据目标函数的值取一个较大的正数）。结合目标函数，其表达式为：

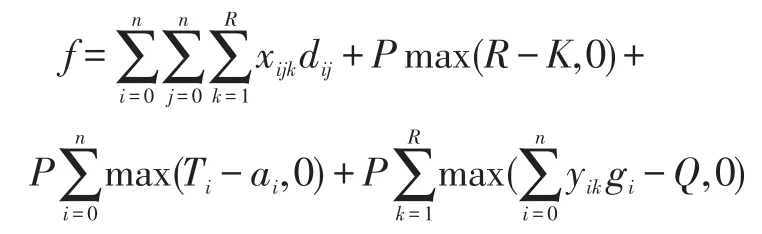
（2）候选解的表示。采用自然数编码的方式表示候选解，且路径条数确定后，如6个节点，3条运送路径的解可表示为0120340560。其中路径1为0-1-2-0，路径2为0-3-4-0，路径3为0-5-6-0。

（3）候选解的产生[4]。任意交换两个节点的位置，便可得到新的候选解，如交换节点1和节点5的位置，新的候选解便为05203416。

（4）降温函数的确定。采用Tk+1=bTk的方式进行降温，其中b为小于1的降温系数。

（5）内循环终止准则。提前设定内循环次数n(Tk)，即每个温度下迭代的步数。

（6）外循环终止准则。通过设定外循环终止温度Tf，或者规定降温次数的上限都可达到终止外循环的目的。

4 实例应用

某地突发地震，现有8个受灾节点需要物资配送，某汽车部队立即出动，准备将驻地救灾物资运往各受灾节点，驻地共有运输车20辆，单车载重量为10t，车速为65km/h，每吨物资的卸载时间为0.15h。各节点相关数据见表1，其中驻地坐标设为（0，0）。

表1 各节点数据

首先，通过计算可得运送路径为3条，即3辆运输车便可满足运输需求。

SAA相关参数的设置为：内循环次数n(Tk)=200，外循环终止温度Tf=10，降温系数b=0.95，初始温度T0=1 200，惩罚因子P=500。通过MATLAB编程，随机求解100次，可得结果见表2。

表2 SAA计算结果

由表2可知，在利用SAA100次的求解过程中，都能得到质量较高的可行解，其中最短运送距离为686km。对应的三条路径分别为:路径1为0-1-8-7-4-0，路径长度为260km,运送时间为5.36h；路径2为0-3-6-0,路径长度为210km,运送时间为4.58h；路径3为0-2-5-0,路径长度为216km,运送时间为4.68h。

5 结束语

采用模拟退火算法对有单边时间窗的配送车辆调度问题进行了求解。从实例应用中可以看出，该算法简单可行，计算效率高，收敛速度快，且能较好地达到全局最优。为解决应急物流的车辆路径问题提供了新思路。

[1]张公让,张勇.基于粒子群算法的应急物流配送车辆调度研究[J].价值工程,2011,(34):9-10.

[2]王惠敏,刘刚.基于模拟退火遗传算法的车辆调度优化[J].微计算机信息,2010,26(11):232-233.

[3]Steinbrunn M,Moerkotte G,Kemper A.Heuristic and Ran2 domized Optimization for the Join Ordering Problem[J].The VLDB Journal,1997,6(3):8-17.

[4]郎茂祥.装卸混合车辆路径问题的模拟退火算法研究[J].系统工程学报,2005,20(5):485-491.

Study on Emergency Logistics Vehicle Dispatching Based on Simulated Annealing Algorithm

Tang Chong
(Student Brigade,Military Transportation Academy,Tianjin 300161,China)

In this paper,in view of the prominent characteristics of emergency logistics,we discussed the optimization of the dispatching route of the emergency logistics vehicles,built the emergency logistics vehicle dispatching model with unilateral time window and designed the simulated annealing algorithm for its solution.

simulatedannealing algorithm;emergency logistics;vehicle dispatching

F252.14;F224.0;U492.3+12

A

1005-152X(2017)01-0114-03

10.3969/j.issn.1005-152X.2017.01.024

2016-12-06

唐冲，男，四川成都人，军事交通学院学生，研究方向：汽车指挥。