基于交通需求的停车换乘点布局优化研究

李雨鸿

（中铁第一勘察设计院集团有限公司，陕西 西安 710043）

基于交通需求的停车换乘点布局优化研究

李雨鸿

（中铁第一勘察设计院集团有限公司，陕西 西安 710043）

在停车换乘可能选择地点集合给定的前提下，从城市交通网络系统的宏观角度出发，以系统内停车换乘站点的建设成本和所有交通需求量的总出行成本之和最小为优化目标，构建了停车换乘站点布局优化模型，最后，借助Lingo商业软件进行算例分析，验证了模型的有效性。

交通需求管理；停车换乘；布局优化；成本效益

1 文献综述

近年来，随着机动车保有量的日益增长，城市交通拥堵问题也日趋严峻。停车换乘方案作为交通需求管理的重要措施之一，对缓解城市交通压力和调节城市交通结构具有重要的作用。停车换乘站点布局研究是停车换乘方案规划的重要组成部分，对停车换乘设施的选址和布局规划的合理与否直接关系到该交通需求管理措施是否能够经济、高效地发挥其交通需求调节作用。文献[1]对北京停车换乘需求进行了调查分析，发现换乘对象主要为通勤者。文献[2]对北京已有的停车换乘（P&R）站点存在的问题进行了分析，指出某些换乘点能力紧张，而有的则能力虚糜，说明其布局存在不合理现象。

在P&R的布局优化研究方面，文献[3]在给定设施的数目并且已知乘客流的线路和流量确定的情况下提出了截流布局优化问题；文献[4]将PIM（Preventative Inspection Model）即危险品监测站布置的思路应用到P&R布局优化中；文献[5]在考虑线性单中心都市的P&R布局时，基于利益最大和社会成本最低的目标提出了一种经济学的优化方法；文献[6]在广义多设施多目标优化选址模型的基础上，以各需求点与临近的供应点之间的总广义费用（出行时间、出行费用）最少为优化目标，提出了多设施多目标P&R布局优化模型；文献[7]以P&R用户广义出行费用最小作为优化目标，建立了P&R布局优化模型，并设计了遗传算法对模型进行求解；文献[8]基于粒子群优化理论，构建了在空间分析上的P&R布局优化截流模型；文献[9]通过评估各个备选点位可达性指标的大小，从而提出一种基于GIS的停车换乘设施优化方法。然而在这些研究中，却很少考虑停车换乘站点建设成本和出行成本的总和，并且对停车换乘设施的能力也缺乏一定的考虑。因此，本文在考虑交通需求量的基础上，综合考虑了停车换乘站点建设成本和所有交通需求量总出行成本，进而对停车换乘站点布局优化进行研究。

2 P&R布局优化一般原则

停车换乘点位置的选择应该遵循一定的原则，由此可以初步确定可选的停车换乘地点，能在一定程度上简化后续的布局优化。主要原则有如下几个方面：（1）停车换乘点应该设在城市客运量较大的运输通道上，与大容量的公共交通系统有机衔接；（2）停车换乘点应该设在其服务范围内小汽车出行发生源最多的地方，并且对服务范围内的小汽车出行具有最大的吸引力；（3）停车换乘点能够为停车换乘者提供最大的便捷程度，如设置在公交线路、轨道交通线路的终点站或是其附近等。就北京而言，除了所要遵循的主要原则以外，还有在四环以内不设置停车换乘点的原则。

3 P&R站点布局的基本模型

在交通枢纽的规划之中，相关模型的研究已非常成熟。传统的方法有一元交通枢纽场站布局的重心法、一元交通枢纽场站布局微分法、成本分析法，经典的枢纽选址布局模型有覆盖模型、平面中位距离模型、特定枢纽选址模型等[10]。

3.1 成本分析法

成本分析法是在已经得到的待选枢纽位置集合（P1,P2,…,Pm）的前提下，以枢纽系统的总成本最小化为目标，通过简单的财务计算，经过比较选择总运输成本最小的点作为最佳的枢纽布局。每个待选点的总费用计算公式如下：

式中：Ri—每个待选枢纽的建设成本；

Wj—每个运输发生源的交通需求发生量；dij—各运输发生源到待选枢纽的距离；

F—相同的单位运输费用。

3.2 覆盖模型（Covering）

这里主要介绍覆盖问题之中的覆盖集问题，该问题是以覆盖所有需求点的最小的选址数作为优化目标函数，旨在用最少的枢纽数覆盖所有的需求点。

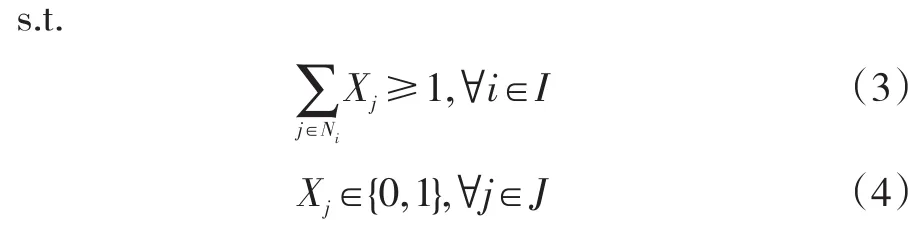
式中：I—所有运输需求点的集合；

J—候选枢纽地点的集合；

dij—需求点i到候选点 j的距离；

Ni={j|dij≤Dc}—能覆盖需求点i的所有候选点的集合，Dc为覆盖距离。

Xj—决策变量，如果在候选点 j选址，则Xj=1；否则Xj=0。

上述两个模型直接应用于停车换乘点布局优化问题中时，存在些许的不足。例如：缺乏对OD需求的考虑，不太符合实际；欠缺对待选停车换乘站点能力的分析；而且目前对于模型（3）中的覆盖距离没有可供参考的成文标准。

4 P&R布局优化模型建立

4.1 模型建立思路

首先根据停车换乘站点布局的一般原则或者其他布局优化模型初步确定候选站点，由定性或定量分析的方法得到一个可能的待选点集合。

考虑将一个城市的区域划分成两个部分，以初步得到的待选停车换乘地点间的虚拟连接线为分界线。在分界线以内，即近似为城市的中心区域，将其看作是交通需求的吸引区域；在分界线以外的部分，即近似为城市的市郊区域，将其看作是交通需求的发生区域。在交通需求的吸引区域假设可以确定固定的交通需求吸引点，例如市区商业中心；相应的可以在交通需求的发生区域确定固定的交通需求发生点，例如城市周边的卫星城。基于交通需求对城市区域进行划分，得到停车换乘点布局的网络结构示意图如图1所示，交通需求发生点O产生的交通需求经过停车换乘点H，最后到达交通需求吸引点D。

图1 停车换乘点网络布局

4.2 模型构建

模型假设：（1）从交通发生点O产生的去往交通吸引点D的交通量中采用停车换乘方案的OD交通量已知；（2）交通发生点产生的交通量可以通过任何一个停车换乘点到达交通吸引点；（3）所有产生交通需求的发生点均在初始给定的待选停车换乘点的吸引范围内；（4）各交通发生点的交通需求量、备选站点的建设费用、停车换乘一次的费用、Oi→Hk和Hk→Dj的费率均已知且为定值。

设在一个城市的交通系统中，有m个交通发生点Oi(i=1,2,…,m)，n个交通吸引点Dj（j=1,2,…,n），经过初步选择得到q个待选停车换乘点Hk（k=1,2,…,q）。以系统内停车换乘点建设成本和所有交通需求量总出行成本最小，辅以相关的约束条件，构建布局优化模型。

式中：W—系统由停车换乘产生的总费用；

Oik—从交通发生点i到待选停车换乘点k的交通量；

Dkj—从待选停车换乘点k到交通吸引点 j的交通量；

Cik—从交通发生点i到待选停车换乘点k的单位费率；

Ckj—从待选停车换乘点k到交通吸引点 j的单位费率；

Ck—停车换乘者在待选点k停车换乘一次的费用；

Fk—待选停车换乘点k的建设费用；

Tij—从交通发生点i到交通吸引点 j的OD交通量；

Ai—交通发生点i的交通发生量；

Pk—待选停车换乘点k的交通容纳能力；

Xk—决策变量，若待选停车换乘点k被选中则Xk=1，否则Xk=0；

M—一个无穷大的正数。

目标函数（5）使得整个城市交通系统中停车换乘的总费用最小；约束（6）从交通发生点i通过各待选换乘站点k到达交通吸引点 j的交通量之和等于发生点i和吸引点 j之间的OD交通量；约束（7）从交通发生点i到待选停车换乘点k的交通量等于发生点i与各吸引点j之间的OD在点k的换乘交通量；约束（8）从待选停车换乘点k到交通吸引点 j的交通量等于各发生点i与吸引点j之间的OD在点k的换乘交通量；约束（9）从交通发生点i到各待选停车换乘点k的交通量之和等于发生点i的发生交通量；约束（10）从交通发生点i到待选停车换乘点k的交通量与从待选停车换乘点k到交通吸引点j的交通量相等；约束（11）是从各交通发生点i到待选停车换乘点k的交通量之和小于待选点k的容纳能力；约束（12）表示待选点与交通量的对应关系，若发生点到待选点k的交通量不为0，则Xk=1，这表示待选点k被选中；约束（13）是关于交通量的非负约束。交通量从发生点通过停车换乘点到吸引点的单位费率Cik和Ckj根据停车换乘者的出行时间、燃油费、以及出行舒适程度等多方面进行综合度量。

5 模型算例分析

假设在某一交通系统中，共有6个交通发生点、5个交通吸引点，按照一定的停车换乘点的布局原则初步得到7个待选点，交通发生点、交通吸引点以及待选停车换乘点的位置关系如图2所示。

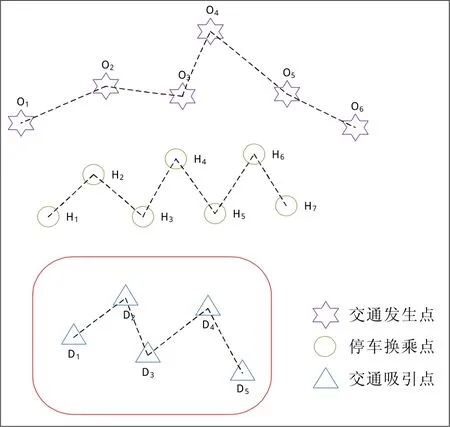
图2 算例示意图

设交通发生点与交通吸引点之间每天的交通量的O-D矩阵见表1，交通发生点与待选停车换乘点之间的费率Cik矩阵见表2，待选停车换乘点与交通吸引点之间的费率Ckj矩阵见表3。

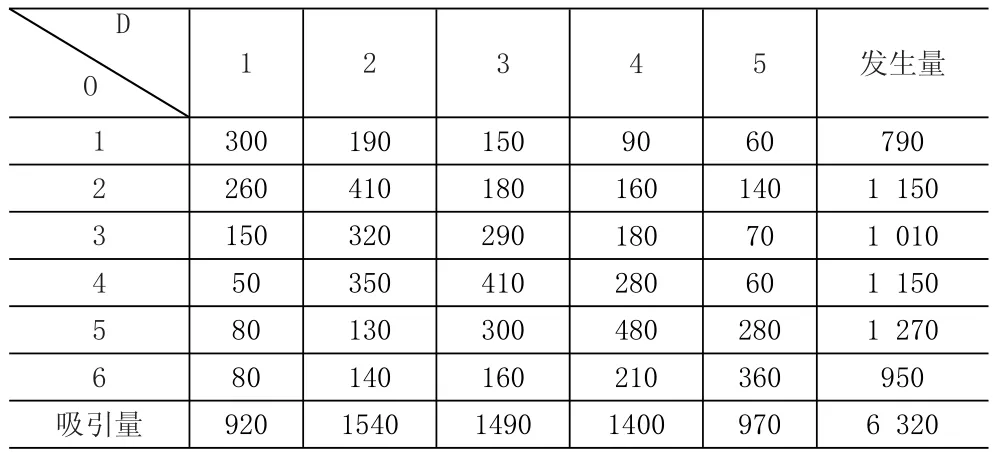
表1 OD表

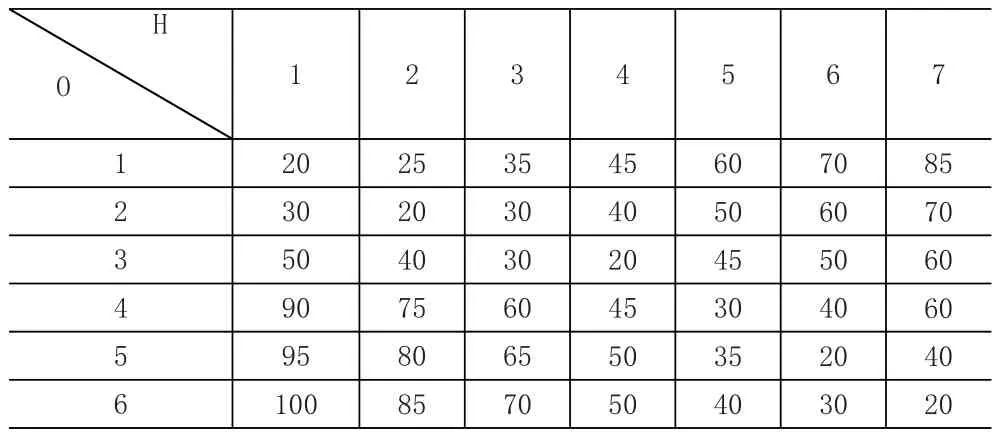
表2 费率Cik矩阵（元）

并设各待选停车换乘点的建设费用平均摊到每天的费用和每停车换乘一次的费用见表4，其容纳能力见表5。

表3 费率Ckj矩阵（元）

表4 换乘点的其他费用（元）

表5 换乘点的容纳能力

基于以上假设数据，利用Lingo数学软件编程对模型进行求解，最终得到在给定初始待选停车换乘点的前提下的布局优化方案。经计算得出，在待选的7个停车换乘点中，选择H2、H3、H5、H7四个待选点作为最终选定的停车换乘布局方案。每个待选点所承担的交通量分别为1 940、1 450、1 730、1 200，系统的总成本为600 480.0元。

6 结论

本文针对停车换乘的交通需求管理方案，对停车换乘的布局优化问题进行了研究，建立了基于交通需求的停车换乘布局优化模型。模型以系统总成本最小为优化目标，综合考虑了交通发生量、换乘点建设成本和停车换乘者的出行成本。本文基于假设数据进行了算例分析，运用了所建立的布局优化模型并借助Lingo对其进行求解，结果表明本文所建模型在停车换乘地点的布局优化方面具备一定的参考价值。在实际规划中可根据一定的布局原则初步确定可行的待选停车候车点，然后再利用布局优化模型对其进一步优化，最终得到合理的、优化的停车换车布局方案。本文的研究内容为进一步加强城市交通需求管理起到了一定的积极作用。

[1]刘燕,秦焕美,潘小松.北京市停车换乘需求调查与分析[J].交通运输工程与信息学报,2011,9(3):118-124.

[2]程左宏.北京市停车换乘措施存在的问题及对策研究[J].道路交通与安全,2010,(4):4-8.

[3]伯曼,霍奇森,克拉斯.截流问题[M].柏林:斯普林格，1995.

[4]马克,霍纳,莎拉.基于网络流的铁路停车换乘设施选址策略[J].社会经济规划科学,2007,(41):255-268.

[5]Judith Wang,HaiYang,Robin Lindsey.确定性模式选择下的线性城市停车换乘设施选址及定价研究[J].运输研究B,2004, (38):709-731.

[6]谢晓倩,徐世凯.停车换乘选址模型研究[J].大连交通大学学报,2012,32(1):17-19.

[7]方青,潘晓东,吴中.基于遗传算法的城市停车换乘设施选址模型研究[J].中国科技论文在线,2010,5(10):763-766.

[8]黄一峰,靳文舟,等.基于粒子群优化理论的停车换乘系统优化选址模型研究[J].城市轨道交通研究,2009,(3):17-21.

[9]刘有军,晏克非.基于GIS的停车换乘设施优化选址方法的研究[J].交通科技,2003,(4):85-87.

[10]何世伟.综合交通枢纽规划理论与方法[M].北京:人民交通出版社,2012.

Study on Layout Optimization of P&R Points Based on Traffic Demand

Li Yuhong
(China Railway First Survey&Design Institute Group Co.,Ltd.,Xi’an 710043,China)

In this paper,upon the premise that the location set for the possible P&R points was given,from a macroscopic perspective of the urban traffic network system,and with minimizing the construction cost of the P&R points in the system and the sum of the total traveling expenses as the optimization objective,we built the P&R point layout optimization model and at the end,through a numerical analysis using the Lingo program,verified the validity of the model.

traffic demandmanagement;P&R;layoutoptimization;cost benefit

F224;U116.2

A

1005-152X(2017)01-0094-04

10.3969/j.issn.1005-152X.2017.01.019

2016-09-09

李雨鸿（1989-），女，硕士研究生，助工，研究方向：交通运输规划与管理。